基于迭代学习和神经网络的机械臂变长度误差跟踪

Variable Length Error Tracking of Manipulator Based on Iterative Learning and Neural Network

摘要: 本文考察了在任意初始状态下不确定性机械臂的轨迹跟踪问题。首先，根据预设期望轨迹、随机变量概率分布函数和虚拟误差变量，建立误差动力学系统。其次，运用虚拟控制信号和迭代学习分别补偿没有运行的区间和处理随机变化的迭代长度。然后，通过自适应神经网络逼近机械臂的不确定性和外部干扰，并通过复合能量函数证明了跟踪算法的可行性。最后，通过一个仿真例子表明了本文算法的有效性。

Abstract: In this paper, trajectory tracking of uncertain manipulator under arbitrary initial conditions is in-vestigated. Firstly, the error dynamics is established according to the preset expected trajectory, the probability distribution function of random variables and the virtual error variable. Secondly, the virtual control signal and iterative learning are used to compensate the interval without opera-tion and the iteration length with random changes. Then, the uncertainty and external disturbance of the manipulator arms are approximated by an adaptive neural network, and the practicability of the tracking algorithm is inspected by a composite energy function. Finally, the simulation example is certified to display the validity of the proposed algorithm.

1. 引言

机械臂在工业领域的广泛应用将人类从繁杂的体力劳动和重复工作中解放出来了。机械臂的物件抓取、机械焊接、油漆喷涂和制造装备等都涉及机械臂的轨迹跟踪问题 [1]。迭代学习控制适用于非线性强耦合和重复性运动的系统，可以广泛应用于机械臂等执行重复任务的被控对象 [2]。机械臂运行过程中信息会丢失一部分，进而会导致每次迭代的长度不一致 [3] [4]。通过神经网络对系统的内部和外部干扰进行逼近，可以提高跟踪控制的精度 [5]。因此，本文通过迭代学习原理和神经网络方法在迭代长度变换的情形下研究机械臂的变长度误差跟踪具有重要意义。

基于自适应模糊迭代学习控制方法，文献 [6] 研究了系统约束和随机变化的迭代长度问题。基于迭代学习控制方法，文献 [7] 研究了一类多输入多输出非线性系统在迭代长度变化的轨迹跟踪问题。基于势垒复合能量函数构造的一种自适应迭代学习控制方法，文献 [8] 研究了在状态对准条件下的多输入多输出非线性系统的变迭代长度轨迹跟踪问题。基于牛顿极值求值算法的迭代学习控制方法，文献 [9] 研究了多轴系统轮廓运动精度控制的问题。基于反馈控制和自适应迭代控制结合的方法，文献 [10] 降低了初始状态不匹配对工业机器人跟踪性能的影响。基于神经网络自适应迭代学习控制方法，文献 [11] 研究了由任意初始偏移引起的问题。基于分布式迭代学习控制方法，文献 [12] 研究了多智能体框架下高速列车速度和位移跟踪控制的问题。基于迭代平均算子的迭代学习控制方法，文献 [13] 研究了具有非均匀迭代长度跟踪的问题。然而，文献 [7] [8] [9] 没有考虑系统的初值变化问题和参数估计值因逐点收敛导致上下界不固定的问题。文献 [11] [12] 没有考虑迭代过程中信息丢失，而造成的迭代不等长的问题。文献 [13] 的控制器设计是基于压缩映射方法，无法使当前迭代的信息充分利用。

综上所述，基于迭代学习控制和神经网络方法，本文将在具有外部干扰和模型不确定性的情况下研究机械臂变长度误差轨迹跟踪问题：1) 与文献 [7] 相比，本文针对任意初始偏移引起的问题，设计期望误差轨迹。2) 与文献 [10] 相比，本文针对迭代学习过程的不等长问题，引入一个虚拟跟踪误差，补偿未运行区间的误差信息。与文献 [13] 相比，本文可以充分利用迭代信息。3) 与文献 [8] 相比，更新率采用饱和函数代替，能够有效避免估计值因逐点收敛导致上下界不固定的问题，且本文考虑了系统的不确定性和外部干扰，用RBF神经网络对其进行逼近，提高精度和收敛性。

2. 问题陈述

考虑机械臂动力学模型：

$\{\begin{array}{l}{\stackrel{\dot{}}{q}}_{1,k}\left(t\right)=q_{2,k}\left(t\right)\\ M\left(q_{1,k}\left(t\right)\right){\stackrel{\dot{}}{q}}_{2,k}+C\left(q_{1,k}\left(t\right),q_{2,k}\left(t\right)\right)q_{2,k}\left(t\right)+G\left(q_{1,k}\left(t\right)\right)={\tau }_k\left(t\right)+d_k\left(t\right)\end{array}$ (1)

其中， $k\in \mathcal{K}=\left\{1,2,\cdots \right\}$ 为迭代次数， $q_{1,k}\left(t\right)\in R^n$ ， $q_{2,k}\left(t\right)\in R^n$ ， ${\stackrel{\dot{}}{q}}_{2,k}\left(t\right)\in R^n$ ，分别为关节位置，关节速度和关节加速度， $M\left(q_{1,k}\left(t\right)\right)\in R^{n\times n}$ 为对称正定的惯性矩阵， $C\left(q_{1,k}\left(t\right),q_{2,k}\left(t\right)\right)\in R^{n\times n}$ 为向心–科里奥利矩阵， $G\left(q_{1,k}\left(t\right)\right)\in R^n$ 为重力矩阵， $d_k\left(t\right)\in R^n$ 为系统模型不确定性和外部扰动在内的有界干扰， ${\tau }_k\left(t\right)\in R^n$ 表示系统控制输入。为了方便后续描述，定义 $M_k\left(q_{1,k}\left(t\right)\right)\triangleq M_k$ ， $C_k\left(q_{1,k}\left(t\right),q_{2,k}\left(t\right)\right)\triangleq C_k$ ， $G_k\left(q_{1,k}\left(t\right)\right)\triangleq G_k$ 。

机械臂有以下特性：

参考文献 [14] [15]，机械臂具有以下特征：

性质1：矩阵 $\left[\stackrel{\dot{}}{M}\left(q_{1,k}\left(t\right)\right)-2C\left(q_{1,k}\left(t\right),q_{2,k}\left(t\right)\right)\right]$ ，是斜对称矩阵，即对任意向量 $x\in R^n$ ， $x^{\text{T}}\left[\stackrel{\dot{}}{M}\left(q_{1,k}\left(t\right)\right)-2C\left(q_{1,k}\left(t\right),q_{2,k}\left(t\right)\right)\right]x=0$

性质2：对于任意的向量 $q,\stackrel{\dot{}}{q}\in R^n$ 和任意的已知向量 $v,\stackrel{\dot{}}{v}\in R^n$ ，存在一个未知的时变参数向量 $\delta \in R^n$ ，使得以下等式成立：

$M\left(q\right)\stackrel{\dot{}}{v}+C\left(q,\stackrel{\dot{}}{q}\right)v+G\left(q\right)=A\left(q,\stackrel{\dot{}}{q},v,\stackrel{\dot{}}{v}\right)\delta$ (2)

其中， $A\left(q,\stackrel{\dot{}}{q},v,\stackrel{\dot{}}{v}\right)\in R^{m\times n}$ 是一个回归矩阵。

引理1 [16] ：对于标量a_i，定义其饱和函数：

$sa{t}_{{\bar{a}}_i}\left(a_i\right)=\{\begin{array}{ll}{\bar{a}}_i^1,\hfill & a_i<{\bar{a}}_i^1\hfill \\ a_i,\hfill & {\bar{a}}_i^1<a_i<{\bar{a}}_i^2\hfill \\ {\bar{a}}_i^2,\hfill & a_i>{\bar{a}}_i^2\hfill \end{array}$ (3)

其中， ${\bar{a}}_i=\left\{{\bar{a}}_i^1,{\bar{a}}_i^2\right\}$ 为a_i的上限和下限，且 ${\bar{a}}_i^1<{\bar{a}}_i^2$ 。

对于向量 $x={\left[x_1,x_2,\cdots ,x_n\right]}^{\text{T}}\in R^n$ 和向量 $y={\left[y_1,y_2,\cdots ,y_n\right]}^{\text{T}}\in R^n$ ，定义 $sa{t}_{\bar{y}}y={\left[sa{t}_{{\bar{y}}_1}\left(y_1\right),sa{t}_{{\bar{y}}_2}\left(y_2\right),\cdots ,sa{t}_{{\bar{y}}_i}\left(y_i\right)\right]}^{\text{T}}\in R^n$ ， ${\bar{y}}_i=\left\{{\bar{y}}_i^1,{\bar{y}}_i^2\right\}$ ， $\bar{y}=\left\{{\bar{y}}_1,{\bar{y}}_2,\cdots ,{\bar{y}}_n\right\}$ 若 ${\bar{y}}_i^1\le x_i\le {\bar{y}}_i^2$ ，则有：

${\left[y-sa{t}_{\bar{y}}\left(y\right)\right]}^{\text{T}}\left[y-sa{t}_{\bar{y}}\left(y\right)\right]\le 0$ (4)

对于矩阵 $A\in R^{m\times n}$ 和 $B\in R^{m\times n}$ ，定义 $sa{t}_{\bar{B}}\left(B\right)={\left\{sa{t}_{{\bar{B}}_{ij}}\left(B_{ij}\right)\right\}}_{m\times n}\in R^{m\times n}$ ，其中 $0\le i\le m,0\le j\le n$ ，且 ${\bar{B}}_{ij}=\left\{{\bar{B}}_{ij}^1,{\bar{B}}_{ij}^2\right\}$ 为 $B_{ij}$ 的上限和下限，若 ${\bar{B}}_{ij}^1\le A_{ij}\le {\bar{B}}_{ij}^2$ ，则有以下不等式成立：

$tr{\left[B-sa{t}_{\bar{B}}\left(B\right)\right]}^{\text{T}}\left[A-sa{t}_{\bar{B}}\left(B\right)\right]\le 0$ (5)

引理2：对于向量 $a,b\in R^n$ 有

$a^{\text{T}}a-b^{\text{T}}b\le 2{\left(a-b\right)}^{\text{T}}a$ (6)

对于矩阵 $A,B\in R^{n\times n}$

$tr\left(A^{\text{T}}A-B^{\text{T}}B\right)\le tr\left[2{\left(A-B\right)}^{\text{T}}A\right]$ (7)

引理3：定义向量 $x\in R^m$ ，向量 $y\in R^n$ 和矩阵 $M\in R^{m\times n}$ ，有：

$y^{\text{T}}{M}^{\text{T}}x=tr\left(y{x}^{\text{T}}M\right)$ (8)

本文做出如下假设：

假设1：在时间 $t\in \left[0,T\right]$ 内，实际轨迹 $q_{1,k}\left(t\right)\in R^n$ 、 $q_2{}_{,k}\left(t\right)\in R^n$ 是连续可导的。

本文中 $T_k$ 是随迭代次数变化的，T是期望迭代长度。对于随机变化的迭代长度问题，需要考虑两种情况， $T_k\le T$ 和 $T_k\ge T$ 。在 $t\in \left[0,T\right]$ 中，迭代在期望长度内，且已经满足下次迭代所需数据。在 $t\in \left[T,T_k\right]$ 中，迭代数据超过期望长度，因此不需要参与下次迭代更新数据，被直接舍去，所以本文只考虑 $T_k\le T$ 的情况。当 $t\in \left[T_k,T\right]$ 时，系统已经完成本次迭代，控制器不再参与系统运行，但更新律仍需将上次的迭代信息记录到未运行区间，使得每次迭代都能是 $\left[0,T\right]$ 的更新信息。根据上述描述，定义 $T_{\min }$ 和 $T_{\max }$ 分别表示 $T_k$ 的最小值和最大值，对 $0<T_{\min }\le T_k\le T_{\max }\triangleq T$ 时设计了控制器。

假设2 [17] ：T_k是一个随机变量，它的概率分布函数为

$F_{T_k}\left(t\right)=P\left[T_k<t\right]=\{\begin{array}{l}0,t\in \left[0,T_{\min }\right]\hfill \\ p\left(t\right),t\in \left(T_{\min },T_{\max }\right]\hfill \\ 1,t\in \left(T_{\max },\infty \right)\hfill \end{array}$ (9)

其中， $0<p\left(t\right)<1$ 是一个连续函数。

注1：假设2描述了随机变量 $T_k$ 的分布情况。当 $F_{T_k}\left(T_{\min }\right)=0$ ，表示 $t\in \left[0,T_{\min }\right]$ ，实际操作长度 $T_k$ 不能大于 $T_{\min }$ ； $F_{T_k}\left(T_{\min }\right)<1$ 时，系统有一定概率运行至最大迭代长度，进而保证在迭代次数趋于无穷时， $T_k=T_{\max }$ 的情况可以出现无穷次。所以概率分布函数 $p\left(t\right)$ 不需要事先知道，这是因为迭代学习控制律的设计与 $p\left(t\right)$ 无关。综上描述假设2是一个通用公式，在大多数实际应用中是满意的。

本文针对系统(1)设计控制器 ${\tau }_k\left(t\right)$ ，使得当迭代次数k趋向于无穷时，关节位置 $q_{1,k}\left(t\right)$ 能够在指定区间 $\left[\xi ,T_k\right]$ 内跟踪期望轨迹 $q_d\left(t\right)$ ，即，在区间 $\left[\xi ,T_k\right]$ ，当 $k\to \infty$ 时，系统以概率1的情况下使 $e_{1,k}\left(t\right)\to 0$ 。

3. 控制设计

3.1. 相关变量设计

定义状态跟踪误差 $e_{\text{1},k}\left(t\right)$ 、 $e_{\text{2},k}\left(t\right)$ 和期望误差轨迹 $e_{1,k}^{*}$ 如下：

$e_{1,k}\left(t\right)\triangleq q_{1,k}\left(t\right)-q_d\left(t\right)$ (10)

$e_{2,k}\left(t\right)\triangleq {\stackrel{\dot{}}{e}}_{1,k}\left(t\right)={\stackrel{\dot{}}{q}}_{1,k}\left(t\right)-{\stackrel{\dot{}}{q}}_d\left(t\right)=q_{2,k}\left(t\right)-{\stackrel{\dot{}}{q}}_d\left(t\right)$ (11)

$e_{1,k}^{*}\left(t\right)\triangleq \left[e_1{}_{,k}\left(0\right)+t{e}_{2,k}\left(0\right)\right]\omega \left(t\right)$ (12)

$\omega \left(t\right)=\{\begin{array}{l}\cos at,t\in \left[0,\xi \right]\\ 0,t\in \left(\xi ,T\right]\end{array}$ (13)

其中，公式中的 $\xi$ 为先前指定的修正时刻。根据公式(10)~公式(12)得到：

$e_{1,k}^{*}\left(0\right)=e_{1,k}\left(0\right)$ (14)

${\stackrel{\dot{}}{e}}_{1,k}^{*}\left(0\right)=e_{2,k}\left(0\right)$ (15)

注2 [18] ：采用了迭代学习控制跟踪的理想条件 $q_{1,k}\left(0\right)=q_d\left(0\right),q_{2,k}\left(0\right)={\stackrel{\dot{}}{q}}_d\left(0\right)$ 来设计控制律。但是在机械臂系统实际运行中，迭代会受到扰动，所以这一条件会被破坏，相关成果不在适用。因此本文通过构造期望误差轨迹(12)来放宽迭代学习控制的初值理想条件，解决迭代初值变化的问题。

当系统(1)运行到 $t=T_k$ 时刻，迭代过程会返回到其初始状态，开始下一次迭代，因此迭代过程只能跟踪时间区间 $0\le t\le T_k$ 的信息。由于 $t=T_k$ 是随机变化的，本文需要设计虚拟误差变量，补偿未运行部分的误差信息。虚拟误差变量设计如下：

${\epsilon }_{1,k}\left(t\right)=e_{1,k}\left(t\right)-e_{1,k}^{*}\left(t\right),{\epsilon }_{2,k}\left(t\right)=e_{2,k}\left(t\right)-{\alpha }_k\left(t\right)$ (16)

$z_{1,k}\left(t\right)=\{\begin{array}{l}{e}_{1,k}\left(t\right)-e_{1,k}^{*}\left(t\right),t\in \left[0,T_k\right]\hfill \\ e_{1,k}\left(T_k\right)-e_{1,k}^{*}\left(T_k\right),t\in \left[T_k,T\right]\hfill \end{array}$ (17)

$z_{2,k}\left(t\right)=\{\begin{array}{l}{e}_{2,k}\left(t\right)-{\alpha }_k\left(t\right),t\in \left[0,T_k\right]\hfill \\ e_{2,k}\left(T_k\right)-{\alpha }_k\left(T_k\right),t\in \left[T_k,T\right]\hfill \end{array}$ (18)

控制器设计分为 $t\in \left[0,T_k\right]$ 和 $t\in \left[T_k,T\right]$ 两个情况讨论。为了证明所提出的迭代学习控制律的收敛性，需要在时间间隔 $T_k\le t\le T$ 内补偿丢失的控制信息。因此引入一个二进制0或1的随机变量 ${\gamma }_k\left(t\right)$ 。 ${\gamma }_k\left(t\right)=1$ 表示系统(1)在第k次迭代的t时刻依旧可以运行，此事件的概率为p(t)。所以 $z_{1,k}\left(t\right)$ 和 $z_{2,k}\left(t\right)$ 可表示为如下：

$z_{1,k}\left(t\right)={\gamma }_k\left(t\right){\epsilon }_{1,k}\left(t\right)+\left(1-{\gamma }_k\left(t\right)\right){\epsilon }_{1,k}\left(T_k\right)$ (19)

$z_{2,k}\left(t\right)={\gamma }_k\left(t\right){\epsilon }_{2,k}\left(t\right)+\left(1-{\gamma }_k\left(t\right)\right){\epsilon }_{2,k}\left(T_k\right)$ (20)

自适应径向基函数神经网络(RBFNN)将用于估计公式(36)中的非线性不确定项d_k(t)。具体表示如下：

${\hat{d}}_k={\hat{W}}_k^{\text{T}}h\left(u_k\right)$ (21)

其中， ${\hat{d}}_k$ 为d_k的估计值， $u_k={\left[e_{1,k}^{*\text{T}},e_{1,k}^{\text{T}},e_{2,k}^{\text{T}},q_{1,k}^{\text{T}},q_{2,k}^{\text{T}},q_d^{\text{T}},{\stackrel{\dot{}}{q}}_d^{\text{T}},{\ddot{q}}_d^{\text{T}}\right]}^{\text{T}}\in R^{8n}$ 为神经网络的控制输入。 ${\hat{W}}_k={\left[{\hat{w}}_{1,k},{\hat{w}}_{2,k},\cdots ,{\hat{w}}_{n,k}\right]}^{\text{T}}\in R^{m\times n}$ 为最优神经网络权值 $W^{*}$ 的估计值，m是隐含层中的神经元节点数。 $h\left(u_k\right)={\left[{\hat{h}}_1\left(u_k\right),{\hat{h}}_2\left(u_k\right),\cdots ,{\hat{h}}_m\left(u_k\right)\right]}^{\text{T}}\in R^m$ 是具有隐层输出函数 $h_j\left(u_k\right)$ 的RBFNN激活函数，高斯函数选择如下：

${\hat{h}}_j\left(u_k\right)=\text{exp}\left[-\frac{{\left(u_k-c_j\right)}^{\text{T}}\left(u_k-c_j\right)}{{\delta }_j^2}\right]$ (22)

其中， $j\in \left\{\mathcal{M}=1,2,\cdots ,m\right\}\$,\$c_j\in R^{8n}$ 是神经元节点的中心， ${\delta }_j$ 是神经元的宽度。存在一组最优神经网络权值 $W^{*}$ 使得以下等式成立：

$d_k=W^{*\text{T}}h\left(u_k\right)+\epsilon \left(u_k\right)$ (23)

其中， $W^{*}$ 定义为如下表达式 [19] ：

$W^{*}=\arg \underset{{\hat{W}}_k\in R^{m\times n}}{\min }\left\{\sup \left|d_k-{\hat{W}}_k^{\text{T}}h\left(u_k\right)\right|\right\}$ (24)

且， $\epsilon \left(u_k\right)$ 为神经网络的逼近误差向量，满足 $\Vert \epsilon \left(u_k\right)\Vert \le {\epsilon }_m$ 。

3.2. 迭代分析

为了让系统(1)在整个迭代过程中保持稳定，分成了两种情况讨论，情况1： $t\in \left[0,T_k\right]$ 和情况2： $t\in \left(T_k,T\right]$ 。

情况1： $t\in \left[0,T_k\right]$ (以下公式中时间t省略)

构造李亚普诺夫函数 $V_k$ ，根据 $V_k$ 设计虚拟控制器 ${\alpha }_k$ ：

$V_k=V_{1,k}+V_{2,k}$ (25)

$V_{1,k}=\frac{1}{2}{z}_{1,k}^{\text{T}}{z}_{1,k}$ (26)

$V_{2,k}=\frac{1}{2}{z}_{2,k}^{\text{T}}{M}_k{z}_{2,k}$ (27)

将公式(26)求导并结合公式(11)和公式(17)有：

$\begin{array}{c}{\stackrel{\dot{}}{V}}_{1,k}=z_{1,k}^{\text{T}}{\stackrel{\dot{}}{z}}_{1,k}=z_{1,k}^{\text{T}}\left[{\stackrel{\dot{}}{e}}_{1,k}-{\stackrel{\dot{}}{e}}_{1,k}^{*}\right]=z_{1,k}^{\text{T}}\left[{\stackrel{\dot{}}{q}}_{1,k}-{\stackrel{\dot{}}{q}}_d-{\stackrel{\dot{}}{e}}_{1,k}^{*}\right]\\ =z_{1,k}^{\text{T}}\left[q_{2,k}-{\stackrel{\dot{}}{q}}_d-{\stackrel{\dot{}}{e}}_{1,k}^{*}\right]=z_{1,k}^{\text{T}}\left[e_{2,k}-{\stackrel{\dot{}}{e}}_{1,k}^{*}\right]\end{array}$ (28)

根据公式(18)得到：

$e_2{}_{,k}=z_2{}_{,k}+{\alpha }_k$ (29)

公式(29)代入公式(28)得到：

${\stackrel{\dot{}}{V}}_{1,k}=z_{1,k}^{\text{T}}\left[z_{2,k}+{\alpha }_k-{\stackrel{\dot{}}{e}}_{1,k}^{*}\right]$ (30)

则设计虚拟控制器为：

${\alpha }_k=-c_1{z}_{1,k}+{\stackrel{\dot{}}{e}}_{1,k}^{*}$ (31)

将公式(31)代入(30)得到：

${\stackrel{\dot{}}{V}}_{1,k}=z_{1,k}^{\text{T}}{z}_{2,k}-c_1{z}_{1,k}^{\text{T}}{z}_{1,k}$ (32)

对公式(27)进行求导得到：

${\stackrel{\dot{}}{V}}_{2,k}=z_{2,k}^{\text{T}}{M}_k{\stackrel{\dot{}}{z}}_{2,k}+\frac{1}{2}{z}_{2,k}^{\text{T}}{\stackrel{\dot{}}{M}}_k{z}_{2,k}$ (33)

公式(33)中，等号右边第一项根据公式(11)和(18)可化简得到：

$z_{2,k}^{\text{T}}{M}_k{\stackrel{\dot{}}{z}}_{2,k}=z_{2,k}^{\text{T}}{M}_k\left({\stackrel{\dot{}}{e}}_{2,k}-{\stackrel{\dot{}}{\alpha }}_k\right)=z_{2,k}^{\text{T}}{M}_k\left({\stackrel{\dot{}}{q}}_{2,k}-{\ddot{q}}_d-{\stackrel{\dot{}}{\alpha }}_k\right)$ (34)

由公式(1)可得到：

$M_k{\stackrel{\dot{}}{q}}_{2.k}={\tau }_k+d_k-C_k{q}_{2,k}-G_k$ (35)

将公式(11)、(18)、(34)和(35)代入公式(33)得到：

$\begin{array}{c}{\stackrel{\dot{}}{V}}_{2,k}=z_{2,k}^{\text{T}}{M}_k{\stackrel{\dot{}}{q}}_{2,k}-z_{2,k}^{\text{T}}{M}_k\left({\ddot{q}}_d+{\stackrel{\dot{}}{\alpha }}_k\right)+\frac{1}{2}{z}_{2,k}^{\text{T}}{\stackrel{\dot{}}{M}}_k{z}_{2,k}\\ =z_{2,k}^{\text{T}}\left({\tau }_k+d_k-C_k{q}_{2,k}-G_k\right)-z_{2,k}^{\text{T}}{M}_k\left({\ddot{q}}_d+{\stackrel{\dot{}}{\alpha }}_k\right)+\frac{1}{2}{z}_{2,k}^{\text{T}}{\stackrel{\dot{}}{M}}_k{z}_{2,k}\\ =z_{2,k}^{\text{T}}\left({\tau }_k+d_k\right)-z_{2,k}^{\text{T}}{C}_k\left({\alpha }_k+z_{2,k}+{\stackrel{\dot{}}{q}}_d\right)-z_{2,k}^{\text{T}}{G}_k-z_{2,k}^{\text{T}}{M}_k\left({\ddot{q}}_d+{\stackrel{\dot{}}{\alpha }}_k\right)+\frac{1}{2}{z}_{2,k}^{\text{T}}{\stackrel{\dot{}}{M}}_k{z}_{2,k}\\ =z_{2,k}^{\text{T}}\left({\tau }_k+d_k\right)-z_{2,k}^{\text{T}}\left[M_k\left({\ddot{q}}_d+{\stackrel{\dot{}}{\alpha }}_k\right)+G_k+C_k\left({\stackrel{\dot{}}{q}}_d+{\alpha }_k\right)\right]+\frac{1}{2}{z}_{2,k}^{\text{T}}\left({\stackrel{\dot{}}{M}}_k-2C_k\right)z_{2,k}\end{array}$ (36)

根据性质1和性质2可得到：

$\begin{array}{c}{\stackrel{\dot{}}{V}}_{2,k}=z_{2,k}^{\text{T}}\left[{\tau }_k+W^{*\text{T}}h\left(u_k\right)+\epsilon \left(u_k\right)-A_k\delta \right]\\ \le z_{2,k}^{\text{T}}\left[{\tau }_k+W^{*\text{T}}h\left(u_k\right)-A_k\delta \right]+\Vert z_{2,k}^{\text{T}}\Vert {\epsilon }_m\end{array}$ (37)

因此，设计的实际控制器为：

${\tau }_k=-z_{1,k}-c_2{z}_{2,k}+A_k{\hat{\delta }}_k-{\hat{W}}_k^{\text{T}}h\left(u_k\right)-{\hat{\epsilon }}_{m,k}\text{sgn}\left(z_{2,k}\right)$ (38)

其中， ${\hat{\delta }}_k$ 为 $\delta$ 的估计， ${\hat{W}}_k$ 为 $W^{*}$ 的估计， ${\hat{\epsilon }}_{m,k}$ 为的 ${\epsilon }_m$ 估计， $c_2$ 大于零的常数。

将公式(38)代入公式(37)得到：

$\begin{array}{c}{\stackrel{\dot{}}{V}}_{2,k}\le z_{2,k}^{\text{T}}\left[-z_{1,k}-c_2{z}_{2,k}+A_k{\hat{\delta }}_k-{\hat{W}}_k^{\text{T}}h\left(u_k\right)-{\hat{\epsilon }}_{m,k}\text{sgn}\left(z_{2,k}\right)-A_k\delta +W^{*\text{T}}h\left(u_k\right)\right]+\Vert z_{2,k}^{\text{T}}\Vert {\epsilon }_m\\ \le z_{2,k}^{\text{T}}\left[-z_{1,k}-c_2{z}_{2,k}+A_k{\hat{\delta }}_k-{\hat{W}}_k^{\text{T}}h\left(u_k\right)-A_k\delta +W^{*\text{T}}h\left(u_k\right)\right]-{\hat{\epsilon }}_{m,k}\Vert z_{2,k}\Vert +{\epsilon }_m\Vert z_{2,k}^{\text{T}}\Vert \end{array}$ (39)

定义

$\delta -{\hat{\delta }}_k\triangleq {\tilde{\delta }}_k,W^{*}-{\hat{W}}_k\triangleq {\tilde{W}}_k,{\epsilon }_m-{\hat{\epsilon }}_{m,k}\triangleq {\tilde{\epsilon }}_{m,k}$ (40)

将公式(40)代入(39)得到：

${\stackrel{\dot{}}{V}}_{2,k}\le -z_{2,k}^{\text{T}}{z}_{1,k}-c_2{z}_{2,k}^{\text{T}}{z}_{2,k}-z_{2,k}^{\text{T}}{A}_k{\tilde{\delta }}_k+z_{2,k}^{\text{T}}{\tilde{W}}_k^{\text{T}}h\left(u_k\right)+{\tilde{\epsilon }}_{m,k}\Vert z_{2,k}\Vert$ (41)

将公式(14)和公式(17)代入公式(26)可得到：

$V_{1,k}\left(0\right)=\frac{1}{2}{z}_{1,k}^{\text{T}}\left(0\right)z_{1,k}\left(0\right)=\frac{1}{2}{\left[e_{1,k}\left(0\right)-e_{1,k}^{*}\left(0\right)\right]}^{\text{T}}\left[e_{1,k}\left(0\right)-e_{1,k}^{*}\left(0\right)\right]=0$ (42)

将公式(15)、公式(17)、公式(18)和公式(31)代入公式(27)可得到：

$\begin{array}{c}{V}_{2,k}\left(0\right)=\frac{1}{2}{z}_{2,k}^{\text{T}}\left(0\right)M_k\left(0\right)z_{2,k}\left(0\right)=\frac{1}{2}{\left[e_{2,k}\left(0\right)-{\alpha }_k\left(0\right)\right]}^{\text{T}}{M}_k\left(0\right)\left[e_{2,k}\left(0\right)-{\alpha }_k\left(0\right)\right]\\ =\frac{1}{2}{\left[e_{2,k}\left(0\right)-c_1{z}_{1,k}\left(0\right)-{\stackrel{\dot{}}{e}}_{1,k}^{*}\left(0\right)\right]}^{\text{T}}{M}_k\left(0\right)\left[e_{2,k}\left(0\right)-c_1{z}_{1,k}\left(0\right)-{\stackrel{\dot{}}{e}}_{1,k}^{*}\left(0\right)\right]=0\end{array}$ (43)

根据公式(32)、公式(41)、公式(42)和公式(43)结合，有：

$\begin{array}{l}{V}_{1,k}+V_{2,k}-V_{1,k-1}-V_{2,k-1}\\ \le V_{1,k}\left(0\right)+V_{2,k}\left(0\right)+{\displaystyle {\int }_0^t\left({\stackrel{\dot{}}{V}}_{1,k}+{\stackrel{\dot{}}{V}}_{2,k}\right)\text{d}\tau }-V_{1,k-1}\\ \le {\displaystyle {\int }_0^t\left(-c_1{z}_{1,k}^{\text{T}}{z}_{1,k}-c_2{z}_{2,k}^{\text{T}}{z}_{2,k}-z_{2,k}^{\text{T}}{A}_k{\tilde{\delta }}_k+z_{2,k}^{\text{T}}{\tilde{W}}_k^{\text{T}}h\left(u_k\right)+{\tilde{\epsilon }}_{m,k}\Vert z_{2,k}\Vert \right)\text{d}\tau }-\frac{1}{2}{z}_{1,k-1}^{\text{T}}{z}_{1,k-1}\end{array}$ (44)

接下来设计 $t\in \left[0,T_k\right]$ 时的更新率设计如下所示：

$\{\begin{array}{l}{\hat{\delta }}_k\left(t\right)=sa{t}_{\bar{\delta }}\left({\bar{\delta }}^{*}{}_k\left(t\right)\right)\hfill \\ {\bar{\delta }}^{*}{}_k\left(t\right)=sa{t}_{\bar{\delta }}\left({\bar{\delta }}^{*}{}_{k-1}\left(t\right)\right)-{\gamma }_1{A}_k^{\text{T}}{z}_{2,k}\hfill \end{array}$ (45)

其中， ${\gamma }_1$ 为大于零的常数， ${\hat{\delta }}_{-1}\left(t\right)=0$ 并且 $\bar{\delta }=\left\{{\bar{\delta }}^1,{\bar{\delta }}^2\right\}$ 表示上限和下限。假设 $\delta \left(t\right)=sa{t}_{\bar{\delta }}\left(\delta \left(t\right)\right)$ ，则 $\delta \left(t\right)$ 在 $\bar{\delta }$ 这个饱和界限内。

$\{\begin{array}{l}{\hat{W}}_k\left(t\right)=sa{t}_{\bar{W}}\left({\bar{W}}_k^{*}\left(t\right)\right)\hfill \\ {\bar{W}}_k^{*}\left(t\right)=sa{t}_{\bar{W}}\left({\bar{W}}_{k-1}^{*}\left(t\right)\right)+{\gamma }_{2}h\left(u_k\right)z_{2,k}^{\text{T}}\hfill \end{array}$ (46)

其中， ${\gamma }_2$ 为大于的常数， ${\hat{W}}_{-1}\left(t\right)=0$ ，并且 $\bar{W}=\left\{{\bar{W}}^1,{\bar{W}}^2\right\}$ 表示上限和下限。假设 $w_{ij}^{*}\left(t\right)=sa{t}_{\bar{W}}\left(w_{ij}^{*}\left(t\right)\right)$ ，则 $w_{ij}^{*}$ 在 $\bar{W}$ 这个饱和界限内。

$\{\begin{array}{l}{\hat{\epsilon }}_{m,k}\left(t\right)=sa{t}_{\bar{\epsilon }}\left({\bar{\epsilon }}^{*}{}_{m,k}\left(t\right)\right)\hfill \\ {\bar{\epsilon }}^{*}{}_{m,k}\left(t\right)=sa{t}_{\bar{\epsilon }}\left({\bar{\epsilon }}_{m,k-1}^{*}\left(t\right)\right)+{\gamma }_3\Vert z_{2,k}\Vert \hfill \end{array}$ (47)

其中， ${\gamma }_3$ 为大于零的常数， ${\hat{\epsilon }}_{m,-1}\left(t\right)=0$ 并且 $\bar{\epsilon }=\left\{{\bar{\epsilon }}^1,{\bar{\epsilon }}^2\right\}$ 表示上限和下限。假设 ${\epsilon }_m=sa{t}_{\bar{\epsilon }}\left({\epsilon }_m\left(t\right)\right)$ ，则 $\bar{\epsilon }$ 这个饱和界限内。

注3：为了保证估计值在预定范围内的有限性，可以使用完全限幅学习律。通过饱和函数的性质，学习算法的整个右侧是饱和的，并且确保每个参数的估计在预先指定的区域内。

情况2： $t\in \left(T_k,T\right]$

在 $t\in \left(T_k,T\right]$ 时的更新率设计如下所示：

${\hat{\delta }}_k\left(t\right)={\hat{\delta }}_{k-1}\left(t\right)$ (48)

${\hat{W}}_k\left(t\right)={\hat{W}}_{k-1}\left(t\right)$ (49)

${\hat{\epsilon }}_{m,k}\left(t\right)={\hat{\epsilon }}_{m,k-1}\left(t\right)$ (50)

其中， ${\hat{\delta }}_{-1}\left(t\right)=0$ ， ${\hat{W}}_{-1}\left(t\right)=0$ ， ${\hat{\epsilon }}_{m,-1}\left(t\right)=0$ 。此时系统(1)已经完成了本次迭代，因此不需要加入控制器，依旧需要保留上一次更新数据。该时刻不参与控制器设计，且不含 $z_{1,k}$ 和 $z_{2,k}$ 的相关信息。

根据更新率(48)~(50)得到：

$\begin{array}{l}{\tilde{\delta }}_k=\delta -{\hat{\delta }}_k=\delta -{\hat{\delta }}_{k-1}={\tilde{\delta }}_{k-1}\\ W_k=W^{*}-{\hat{W}}_k=W^{*}-{\hat{W}}_{k-1}={\tilde{W}}_{k-1}\\ {\tilde{\epsilon }}_{m,k}={\epsilon }_m-{\hat{\epsilon }}_{m,k}={\epsilon }_m-{\hat{\epsilon }}_{m,k-1}={\tilde{\epsilon }}_{m,k-1}\end{array}$ (51)

当k = 0时，得到如下等式：

$\begin{array}{l}{\tilde{\delta }}_0=\delta -{\hat{\delta }}_0=\delta -{\hat{\delta }}_{-1}=\delta \\ W_0=W^{*}-{\hat{W}}_0=W^{*}-{\hat{W}}_{-1}=W^{*}\\ {\tilde{\epsilon }}_{m,0}={\epsilon }_m-{\hat{\epsilon }}_{m,0}={\epsilon }_m-{\hat{\epsilon }}_{m,-1}={\epsilon }_m\end{array}$ (52)

引理4：对于常数 ${\tilde{\epsilon }}_{m,k}$ ，向量 ${\tilde{\delta }}_k\in R^n$ ，矩阵 ${\tilde{W}}_k\in R^{m\times n}$ ，分别有：

$\begin{array}{l}{\tilde{\epsilon }}_{m,k}^2-{\tilde{\epsilon }}_{m,k-1}^2\le -2{\gamma }_3\Vert z_{2,k}\Vert {\tilde{\epsilon }}_{m,k}\\ {\tilde{\delta }}_k^{\text{T}}{\tilde{\delta }}_k-{\tilde{\delta }}_{k-1}^{\text{T}}{\tilde{\delta }}_{k-1}\le 2{\gamma }_1{z}_{2,k}^{\text{T}}{A}_k{\tilde{\delta }}_k\\ tr\left({\tilde{W}}_k^{\text{T}}{\tilde{W}}_k\right)-tr\left({\tilde{W}}_{k-1}^{\text{T}}{\tilde{W}}_{k-1}\right)\le -2{\gamma }_2{z}_{2,k}^{\text{T}}{\tilde{W}}_k^{\text{T}}h\left(u_k\right)\end{array}$ (53)

引理5：对于常数 ${\tilde{\epsilon }}_{m,0}$ ，向量 ${\tilde{\delta }}_0\in R^n$ ，矩阵 ${\tilde{W}}_0\in R^{m\times n}$ ，分别有：

$\begin{array}{l}\frac{1}{2{\gamma }_3}{\tilde{\epsilon }}_{m,0}^2\le -{\tilde{\epsilon }}_{m,0}\Vert z_{2,0}\Vert +\frac{1}{2{\gamma }_3}{\epsilon }_m^2\\ \frac{1}{2{\gamma }_1}{\tilde{\delta }}_0^{\text{T}}{\tilde{\delta }}_0\le z_{2,0}^{\text{T}}{A}_0{\tilde{\delta }}_0+\frac{1}{2{\gamma }_1}{\delta }^{\text{T}}\delta \\ \frac{1}{2{\gamma }_2}tr\left({\tilde{W}}_0^{\text{T}}{\tilde{W}}_0\right)\le -z_{2,0}^{\text{T}}{\tilde{W}}_0^{\text{T}}h\left(u_0\right)+\frac{1}{2{\gamma }_2}tr\left(W^{*\text{T}}{W}^{*}\right)\end{array}$ (54)

4. 稳定性分析

定理1：根据机械臂系统(1)，在设计的控制律(38)和更新率(45)~(50)下，保证迭代次数k趋于无穷大时，跟踪误差以概率为1在 $\left[\xi ,T_k\right]$ 上收敛到零。

证明：整个证明过程分了三个步骤，分别为步骤1：证明复合能量函数随迭代次数单调递减，步骤2：证明k = 0时，复合能量函数在 $\left[0,T\right]$ 是有界的，步骤3：证明关节位置 $q_{1,k}$ 能够实现对期望轨迹 $q_d$ 的跟踪。

步骤1：证明复合能量函数随迭代次数单调递减。

情况1： $t\in \left[0,T_k\right]$ (以下公式中时间t省略)。

设计复合能量函数 $E_k^{\left(1\right)}$ 如下：

$E_k^{\left(1\right)}=V_k+\frac{1}{2{\gamma }_1}{\displaystyle {\int }_0^t{\tilde{\delta }}_k^{\text{T}}}{\tilde{\delta }}_k\text{d}\tau +\frac{1}{2{\gamma }_2}{\displaystyle {\int }_0^{t}tr}\left({\tilde{W}}_k^{\text{T}}{\tilde{W}}_k\right)\text{d}\tau +\frac{1}{2{\gamma }_3}{\displaystyle {\int }_0^t{\tilde{\epsilon }}_{m,k}^2}\text{d}\tau$ (55)

根据公式(25)和公式(55)得到：

$\begin{array}{c}{E}_k^{\left(1\right)}=V_k\left(0\right)+{\displaystyle {\int }_0^t{\stackrel{\dot{}}{V}}_k\left(\tau \right)\text{d}\tau }+\frac{1}{2{\gamma }_1}{\displaystyle {\int }_0^t{\tilde{\delta }}_k^{\text{T}}}{\tilde{\delta }}_k\text{d}\tau +\frac{1}{2{\gamma }_2}{\displaystyle {\int }_0^{t}tr}\left({\tilde{W}}_k^{\text{T}}{\tilde{W}}_k\right)\text{d}\tau +\frac{1}{2{\gamma }_3}{\displaystyle {\int }_0^t{\tilde{\epsilon }}_{m,k}^2}\text{d}\tau \\ =V_{1,k}\left(0\right)+V_{2,k}\left(0\right)+{\displaystyle {\int }_0^t\left[{\stackrel{\dot{}}{V}}_{1,k}\left(\tau \right)+{\stackrel{\dot{}}{V}}_{2,k}\left(\tau \right)\right]\text{d}\tau }+\frac{1}{2{\gamma }_1}{\displaystyle {\int }_0^t{\tilde{\delta }}_k^{\text{T}}{\tilde{\delta }}_k}\text{d}\tau \\ +\frac{1}{2{\gamma }_2}{\displaystyle {\int }_0^{t}tr}\left({\tilde{W}}_k^{\text{T}}{\tilde{W}}_k\right)\text{d}\tau +\frac{1}{2{\gamma }_3}{\displaystyle {\int }_0^t{\tilde{\epsilon }}_{m,k}^2}\text{d}\tau \end{array}$ (56)

结合公式(42)和公式(43)，公式(56)可化简得到：

$E_k^{\left(1\right)}={\displaystyle {\int }_0^t\left[{\stackrel{\dot{}}{V}}_{1,k}\left(\tau \right)+{\stackrel{\dot{}}{V}}_{2,k}\left(\tau \right)\right]\text{d}\tau }+\frac{1}{2{\gamma }_1}{\displaystyle {\int }_0^t{\tilde{\delta }}_k^{\text{T}}{\tilde{\delta }}_k}\text{d}\tau +\frac{1}{2{\gamma }_2}{\displaystyle {\int }_0^{t}tr}\left({\tilde{W}}_k^{\text{T}}{\tilde{W}}_k\right)\text{d}\tau +\frac{1}{2{\gamma }_3}{\displaystyle {\int }_0^t{\tilde{\epsilon }}_k^2}\text{d}\tau$ (57)

迭代到第k次的差值为 $\Delta E_k^{\left(1\right)}=E_k^{\left(1\right)}-E_{k-1}^{\left(1\right)}$ ，则有：

$\begin{array}{c}\Delta E_k^{\left(1\right)}=E_k^{\left(1\right)}-E_{k-1}^{\left(1\right)}\\ =V_{1,k}+V_{2,k}-V_{1,k-1}-V_{2,k-1}+\frac{1}{2{\gamma }_1}{\displaystyle {\int }_0^t\left({\tilde{\delta }}_k^{\text{T}}{\tilde{\delta }}_k-{\tilde{\delta }}_{k-1}^{\text{T}}{\tilde{\delta }}_{k-1}\right)\text{d}\tau }\\ +\frac{1}{2{\gamma }_2}{\displaystyle {\int }_0^{t}tr}\left[\left({\tilde{W}}_k^T{\tilde{W}}_k\right)-tr\left({\tilde{W}}_{k-1}^{\text{T}}{\tilde{W}}_{k-1}\right)\right]\text{d}\tau +\frac{1}{2{\gamma }_3}{\displaystyle {\int }_0^t\left({\tilde{\epsilon }}_k^2-{\tilde{\epsilon }}_{k-1}^2\right)\text{d}\tau }\end{array}$ (58)

将公式(44)和引理4代入公式(58)得到：

$\begin{array}{c}\Delta E_k^{\left(1\right)}\le {\displaystyle {\int }_0^t\left(-c_1{z}_{1,k}^{\text{T}}{z}_{1,k}-c_2{z}_{2,k}^{\text{T}}{z}_{2,k}-z_{2,k}^{\text{T}}{A}_k{\tilde{\delta }}_k+z_{2,k}^{\text{T}}{\tilde{W}}_k^{\text{T}}h\left(u_k\right)+{\tilde{\epsilon }}_{m,k}\Vert z_{2,k}\Vert \right)\text{d}\tau }-\frac{1}{2}{z}_{1,k-1}^{\text{T}}{z}_{1,k-1}\\ +\frac{1}{2{\gamma }_1}{\displaystyle {\int }_0^{t}2}{\gamma }_1{z}_{2,k}^{\text{T}}{A}_k{\tilde{\delta }}_k\text{d}\tau +\frac{1}{2{\gamma }_2}{\displaystyle {\int }_0^t-}2{\gamma }_2{z}_{2,k}^{\text{T}}{\tilde{W}}_k^{\text{T}}h\left(u_k\right)\text{d}\tau +\frac{1}{2{\gamma }_3}{\displaystyle {\int }_0^t-}2{\gamma }_3\Vert z_{2,k}\Vert {\tilde{\epsilon }}_{m,k}\text{d}\tau \\ \le {\displaystyle {\int }_0^t\left(-c_1{z}_{1,k}^{\text{T}}{z}_{1,k}-c_2{z}_{2,k}^{\text{T}}{z}_{2,k}\right)\text{d}\tau }-\frac{1}{2}{z}_{1,k-1}^{\text{T}}{z}_{1,k-1}\le 0\end{array}$ (59)

情况2： $t\in \left(T_k,T\right]$ 。

设计复合能量函数 $E_k\left(t\right)$ 如下：

$E_k\left(t\right)=E_k^{\left(1\right)}\left(T_k\right)+E_k^{\left(2\right)}\left(t\right)$ (60)

其中， $E_k^{\left(1\right)}\left(T_k\right)$ 是情况1在 $T_k$ 时刻的复合能量函数。公式(60)中 $E_k^{\left(2\right)}\left(t\right)$ 设计如下：

$E_k^{\left(2\right)}\left(t\right)=\frac{1}{2{\gamma }_1}{\displaystyle {\int }_{T_k}^t{\tilde{\delta }}_k^{\text{T}}}{\tilde{\delta }}_k\text{d}\tau +\frac{1}{2{\gamma }_2}{\displaystyle {\int }_{T_k}^{t}tr}\left({\tilde{W}}_k^{\text{T}}{\tilde{W}}_k\right)\text{d}\tau +\frac{1}{2{\gamma }_3}{\displaystyle {\int }_{T_k}^t{\tilde{\epsilon }}_{m,k}^2}\text{d}\tau$ (61)

根据情况1得到， $\Delta E_k^{\left(1\right)}\left(T_k\right)\le 0$ 。现在只需证明 $E_k^{\left(2\right)}\left(t\right)$ 是随迭代次数单调递减的。根据公式(61)得：

$\begin{array}{c}\Delta E_k^{\left(2\right)}\left(t\right)=E_k^{\left(2\right)}\left(t\right)-E_{k-1}^{\left(2\right)}\left(t\right)\\ =\frac{1}{2{\gamma }_1}{\displaystyle {\int }_0^t\left({\tilde{\delta }}_k^{\text{T}}{\tilde{\delta }}_k-{\tilde{\delta }}_{k-1}^{\text{T}}{\tilde{\delta }}_{k-1}\right)\text{d}\tau }+\frac{1}{2{\gamma }_2}{\displaystyle {\int }_0^{t}tr}\left[\left({\tilde{W}}_k^{\text{T}}{\tilde{W}}_k\right)-tr\left({\tilde{W}}_{k-1}^{\text{T}}{\tilde{W}}_{k-1}\right)\right]\text{d}\tau \\ +\frac{1}{2{\gamma }_3}{\displaystyle {\int }_0^t\left({\tilde{\epsilon }}_k^2-{\tilde{\epsilon }}_{k-1}^2\right)\text{d}\tau }\end{array}$ (62)

将公式(51)代入公式(62)得到：

$\Delta E_k^{\left(2\right)}\left(t\right)=0$ (63)

$\Delta E_k\left(t\right)=\Delta E_k^{\left(1\right)}\left(T_k\right)+\Delta E_k^{\left(2\right)}\left(t\right)$ (64)

根据情况2描述， $\Delta E_k\left(t\right)$ 在 $\left(T_k,T\right]$ 上小于等于0。

综上所述，根据情况1和情况2分析，复合能量函数在[0, T]区间上任意时刻的值随迭代次数增加而单调减。

步骤2：证明k = 0时，复合能量函数在 $\left[0,T\right]$ 是有界的。

情况1： $\left[0,T\right]$ (以下公式中时间t省略)。

根据公式(55)可得到：

$E_0^{\left(1\right)}=V_{1,0}+V_{2,0}+\frac{1}{2{\gamma }_1}{\displaystyle {\int }_0^t{\tilde{\delta }}_0^{\text{T}}{\tilde{\delta }}_0}\text{d}\tau +\frac{1}{2{\gamma }_2}{\displaystyle {\int }_0^{t}tr}\left(W_0^{\text{T}}{W}_0\right)\text{d}\tau +\frac{1}{2{\gamma }_3}{\displaystyle {\int }_0^t{\tilde{\epsilon }}_{m,0}^2}\text{d}\tau$ (65)

对公式(65)进行求导得到：

${\stackrel{\dot{}}{E}}_0^{\left(1\right)}={\stackrel{\dot{}}{V}}_{1,0}+{\stackrel{\dot{}}{V}}_{2,0}+\frac{1}{2{\gamma }_1}{\tilde{\delta }}_0^{\text{T}}{\tilde{\delta }}_0+\frac{1}{2{\gamma }_2}tr\left(W_0^{\text{T}}{W}_0\right)+\frac{1}{2{\gamma }_3}{\tilde{\epsilon }}_{m,0}^2$ (66)

将公式(32)、(41)和引理5代入公式(66)：

$\begin{array}{c}{\stackrel{\dot{}}{E}}_0^{\left(1\right)}\le -c_1{z}_{1,0}^{\text{T}}{z}_{1,0}-c_2{z}_{2,0}^{\text{T}}{z}_{2,0}-z_{2,0}^{\text{T}}{A}_0{\tilde{\delta }}_0+z_{2,0}^{\text{T}}{\tilde{W}}_0^{\text{T}}h\left(u_0\right)+{\tilde{\epsilon }}_{m,0}\Vert z_{2,0}\Vert +z_{2,0}^{\text{T}}{A}_0{\tilde{\delta }}_0\\ -z_{2,0}^{\text{T}}{\tilde{W}}_0^{\text{T}}h\left(u_0\right)-{\tilde{\epsilon }}_{m,0}\Vert z_{2,0}\Vert +\frac{1}{2{\gamma }_1}{\delta }^{\text{T}}\delta +\frac{1}{2{\gamma }_2}tr\left(W^{*\text{T}}{W}^{*}\right)+\frac{1}{2{\gamma }_3}{\epsilon }_m^2\\ \le -c_1{z}_{1,0}^{\text{T}}{z}_{1,0}-c_2{z}_{2,0}^{\text{T}}{z}_{2,0}+\frac{1}{2{\gamma }_1}{\delta }^{\text{T}}\delta +\frac{1}{2{\gamma }_0}tr\left(W^{*\text{T}}{W}^{*}\right)+\frac{1}{2{\gamma }_0}{\epsilon }_m^2\le L\end{array}$ (67)

其中， $L={\delta }^{\text{T}}\delta +tr\left(W^{*}{}^{\text{T}}{W}^{*}\right)+{\epsilon }_m^2$ ，L是一个大于等于零的常数。则 $E_0^{\left(1\right)}\le E_0^{\left(1\right)}\left(0\right)+T_{k}L<\infty$ ，即 $E_0^{\left(1\right)}$ 在 $\left[0,T_k\right]$ 内有界。

情况2： $t\in \left(T_k,T\right]$

根据公式(60)可得：

$E_0\left(t\right)=E_0^{\left(1\right)}\left(T_k\right)+E_0^{\left(2\right)}\left(t\right)$ (68)

其中， $E_0^{\left(1\right)}\left(T_k\right)$ 是情况1在 $T_k$ 时刻的复合能量函数，根据情况1得到， $E_0^{\left(1\right)}\left(T_k\right)$ 是有界的。现在只需证明 $E_0^{\left(2\right)}\left(t\right)$ 是有界的。根据公式(61)得到 $E_0^{\left(2\right)}\left(t\right)$ ：

$E_0^{\left(2\right)}\left(t\right)=\frac{1}{2{\gamma }_1}{\displaystyle {\int }_{T_k}^t{\tilde{\delta }}_0^{\text{T}}{\tilde{\delta }}_0}\text{d}\tau +\frac{1}{2{\gamma }_2}{\displaystyle {\int }_{T_k}^{t}tr}\left({\tilde{W}}_0^{\text{T}}{\tilde{W}}_0\right)\text{d}\tau +\frac{1}{2{\gamma }_3}{\displaystyle {\int }_{T_t}^t{\tilde{\epsilon }}_{m,0}^2}\text{d}\tau$ (69)

将公式(52)代入公式公式(69)可得到：

$E_0^{\left(2\right)}\left(t\right)=\frac{1}{2{\gamma }_1}{\displaystyle {\int }_{T_k}^t{\delta }^{\text{T}}}\delta \text{d}\tau +\frac{1}{2{\gamma }_2}{\displaystyle {\int }_{T_k}^{t}tr}\left(W^{*\text{T}}{W}^{*}\right)\text{d}\tau +\frac{1}{2{\gamma }_3}{\displaystyle {\int }_{T_k}^t{\epsilon }_m^2}\text{d}\tau$ (70)

因为 $\delta \left(t\right),W^{*}\left(t\right),{\epsilon }_m\left(t\right)$ 在 $\left[0,T_k\right]$ 是连续且有界的，所以存在常数 $l_1,l_2,l_3$ 使得 [20] ：

$\begin{array}{l}{l}_1={\max }_{t\in \left[0,T_k\right]}\left(\frac{1}{2{\gamma }_1}{\delta }^{\text{T}}\delta \right)<\infty \\ l_2={\max }_{t\in \left[0,T_k\right]}\left[\frac{1}{2{\gamma }_2}tr\left(W^{*\text{T}}{W}^{*}\right)\right]<\infty \\ l_3={\max }_{t\in \left[0,T_k\right]}\left(\frac{1}{2{\gamma }_2}{\epsilon }_m^2\right)<\infty \end{array}$ (71)

将公式(71)代入公式(70)得到：

$\begin{array}{c}{E}_0^{\left(2\right)}\left(t\right)=\frac{1}{2{\gamma }_1}{\displaystyle {\int }_{T_k}^t{l}_1}\text{d}\tau +\frac{1}{2{\gamma }_2}{\displaystyle {\int }_{T_k}^t{l}_2}\text{d}\tau +\frac{1}{2{\gamma }_3}{\displaystyle {\int }_{T_k}^t{l}_3}\text{d}\tau \\ \le \frac{T-T_k}{2{\gamma }_1}{l}_1+\frac{T-T_k}{2{\gamma }_2}{l}_2+\frac{T-T_k}{2{\gamma }_3}{l}_3\le \infty \end{array}$ (72)

根据公式(72)得到， $E_0^{\left(2\right)}\left(t\right)$ 是有界的。所以 $E_0\left(t\right)$ 在 $\left(T_k,T\right]$ 是有界的。根据情况1和情况2描述，得到复合能量函数在[0, T]是有界的。

步骤3：证明关节位置 $q_{1,k}$ 能够实现对期望轨迹 $q_d$ 的跟踪。

根据步骤1和步骤2得到在 $t\in \left[0,T_k\right]$ 时：

$\begin{array}{c}{E}_k^{\left(1\right)}\left(t\right)\le E_0^{\left(1\right)}\left(t\right)+{\displaystyle \underset{j=1}{\overset{k}{\sum }}\Delta }{E}_j^{\left(1\right)}\left(t\right)\\ \le E_0^{\left(1\right)}\left(t\right)-{\displaystyle \underset{j=1}{\overset{k}{\sum }}{\displaystyle {\int }_0^t\left[c_1{z}_{1,j}^{\text{T}}{z}_{1,j}+c_2{z}_{2,j}^{\text{T}}{z}_{2,j}\right]\text{d}\tau }}-{\displaystyle \underset{j=0}{\overset{k-1}{\sum }}\frac{1}{2}{z}_{1,j}^{\text{T}}{z}_{1,j}}\end{array}$ (73)

公式(73)进一步可得：

${\displaystyle \underset{j=1}{\overset{k}{\sum }}{\displaystyle {\int }_0^t\left(c_1{z}_{1,j}^{\text{T}}{z}_{1,j}+c_2{z}_{2,j}^{\text{T}}{z}_{2,j}\right)\text{d}\tau }}+{\displaystyle \underset{j=0}{\overset{k-1}{\sum }}\frac{1}{2}{z}_{1,j}^{\text{T}}{z}_{1,j}}\le E_0^{\left(1\right)}\left(t\right)-E_k^{\left(1\right)}\left(t\right)\le \infty$ (74)

根据假设2 [21] 可得， ${\gamma }_k\left(t\right)=0$ 时，系统迭代到第k次的t时刻已经停止运行。 ${\gamma }_k\left(t\right)=1$ 时，系统迭代到第k次的t时刻依旧在运行。根据公式(17)、公式(19)和公式(74)，当迭代k趋于无穷时得：

$\begin{array}{c}{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{z}_{1,k}^{\text{T}}}{z}_{1,k}={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\gamma }_k}\left(t\right){\epsilon }_{1,k}{\left(t\right)}^{\text{T}}{\epsilon }_{1,k}\left(t\right)\\ ={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\gamma }_k}\left(t\right){\left[e_{1,k}\left(t\right)-e_{1,k}^{*}\left(t\right)\right]}^{\text{T}}\left[e_{1,k}\left(t\right)-e_{1,k}^{*}\left(t\right)\right]\le \infty \end{array}$ (75)

所以，当系统的迭代次数 $k\to \infty$ 时，系统 ${\gamma }_k\left(t\right)=1$ 成立，使得 $e_{1,k}\left(t\right)-e_{1,k}^{*}\left(t\right)$ 收敛到0，即关节误差 $e_{1,k}\left(t\right)$ 可以跟踪到期望误差轨迹所以根据本文设计的期望轨迹误差(12)可得，在时间 $\left[\xi ,T_k\right]$ 上关节误差 $e_{1,k}$ 以概率1收敛至0，意味着关节位置 $q_{1,k}$ 能够实现对期望轨迹 $q_d$ 的跟踪。

5. 仿真实验

本文考虑一个2自由度机械臂系统：

$\{\begin{array}{l}{\stackrel{\dot{}}{q}}_{1,k}\left(t\right)=q_{2,k}\left(t\right)\hfill \\ M\left(q_{1,k}\left(t\right)\right){\stackrel{\dot{}}{q}}_{2,k}+C\left(q_{1,k}\left(t\right),q_{2,k}\left(t\right)\right)q_{2,k}\left(t\right)+G\left(q_{1,k}\left(t\right)\right)={\tau }_k\left(t\right)+d_k\left(t\right)\hfill \end{array}$ (76)

其中， $q_{1,k}={\left[q_{11,k},q_{12,k}\right]}^{\text{T}}$ ， $q_{2,k}={\left[q_{12,k},q_{22,k}\right]}^{\text{T}}$ ， $M\left(q_{1,k}\right)={\left[M_{ij}\right]}_{2\times 2}$ ， $M_{11}=m_1{l}_1^2+m_2\left(l_1^2+l_2^2+2l_1{l}_2\cos \left(q_{12,k}\right)\right)$ ， $M_{12}=M_{21}=m_2\left(l_2^2+l_1{l}_2\cos \left(q_{12,k}\right)\right)$ ， $M_{22}=m_2{l}_2^2$ ， $C\left(q_{1,k},q_{2,k}\right)={\left[C_{ij}\right]}_{2\times 2}$ ， $C_{11}=-m_2{l}_1{l}_2{q}_{22,k}\sin q_{12,k}$ ， $C_{12}=-m_2{l}_1{l}_2\sin \left(q_{12,k}\right)\left(q_{21,k}+q_{22,k}\right)$ ， $C_{21}=m_2{l}_1{l}_2{q}_{21,k}\sin \left(q_{12,k}\right)$ ， $C_{22}=0$ ， $G\left(q_{1,k}\right)={\left[G_1,G_2\right]}^{\text{T}}$ ， $G_1=\left(m_1+m_2\right)l_{1}g\cos \left(q_{11,k}\right)+m_2{l}_{2}g\cos \left(q_{11,k}+q_{12,k}\right)$ ， $G_2=m_2{l}_{2}g\cos \left(q_{11,k}+q_{12,k}\right)$ 。回归矩阵 $A_{11}=l_1^2\left({\ddot{q}}_{d1}+{\stackrel{\dot{}}{\alpha }}_{1,k}\right)+l_{1}g\cos \left(q_{11,k}\right)$ ， $A_{21}=0$ ， $\begin{array}{l}{A}_{12}=\left(l_1^2+l_2^2+2l_1{l}_2\cos \left(q_{12,k}\right)\right)\left({\ddot{q}}_{d1}+{\stackrel{\dot{}}{\alpha }}_{1,k}\right)-(\left({\stackrel{\dot{}}{q}}_{d1}+{\alpha }_{1,k}\right)q_{22,k}+\left({\stackrel{\dot{}}{q}}_{d1}+{\alpha }_{1,k}\right)\\ \cdot \left(q_{21,k}+q_{22,k}\right))l_1{l}_2\sin \left(q_{12,k}\right)+l_{1}g\cos \left(q_{11,k}\right)+l_{2}g\cos \left(q_{11,k}+q_{12,k}\right)\end{array}$ $A_{22}=l_2^2+l_1{l}_2\cos \left(q_{12,k}\right))\left({\ddot{q}}_{d1}+{\stackrel{\dot{}}{\alpha }}_{1,k}\right)+l_2^2\left({\ddot{q}}_{d2}+{\stackrel{\dot{}}{\alpha }}_{2,k}\right)+\left({\stackrel{\dot{}}{q}}_{d1}+{\alpha }_{1,k}\right)q_{21,k}{l}_1{l}_2\sin \left(q_{12,k}\right)+l_{2}g\cos \left(q_{11,k}+q_{12,k}\right)$ 。

系统的期望轨迹q_d表示为 ${\left[0.4\sin \left(0.5\pi t\right),0.4\cos \left(\pi t\right)\right]}^{\text{T}}$ ，期望迭代长度 $T_{\max }$ 设置为6 s， $T_k$ 分布在[4, 6] s，初值 $q_{\text{1},k}\left(0\right)={\left[\text{rand}\left(\text{1}\right),0.\text{8rand}\left(\text{1}\right)\right]}^{\text{T}}$ ，机械臂系统参数设置为 $l_{\text{1}}=l_{\text{2}}=0.\text{8}\text{m}$ ， $g=9.81\text{m}/\text{s}$ ， $m_{\text{1}}=m_{\text{2}}=\text{1}\text{kg}$ ， $d_k={\left[0.1\sin t,0.1\cos t\right]}^{\text{T}}$ 。

定义性能指标 $avg\left(\Vert z_{1,k}\left(t\right)\Vert \right)=\frac{{\displaystyle \underset{i=1}{\overset{T_k}{\sum }}\left(\Vert z_{1,k}\left(i\cdot t_s\right)\Vert \right)}}{T_k/t_s}$ 和表现跟踪状态随迭代次数变化 $J_{\max }={\max }_{t\in \left[0,T_k\right]}\left(\Vert z_{1,k}\Vert \right)$ 。其中 $T_k$ 表示迭代长度， $t_s$ 表示采样间隔。

P1：采用本文设计实际控制器(38)和更新率(45)~(47)。

P2：机械臂自适应迭代学习控制，控制器设计为 ${\tau }_k={\stackrel{\dot{}}{e}}_{1,k}\left(t\right)-c_2{e}_{1,k}\left(t\right)-{\hat{d}}_k\left(t\right)\mathrm{sgn}\left({\stackrel{\dot{}}{e}}_{1,k}\left(t\right)\right)$ ，迭代自适应参数更新率设计为 ${\hat{d}}_k\left(t\right)=sa{t}_{\bar{d}}\left({\hat{d}}_{k-1}\left(t\right)\right)+\Gamma e_{1,k}^{\text{T}}\left(t\right)\mathrm{sgn}\left({\stackrel{\dot{}}{e}}_{1,k}\left(t\right)\right)$ 。

Figure 1. Joint position q_11,k and expected position signal q_d1

图1. 关节位置q_11,k和期望位置信号q_d1

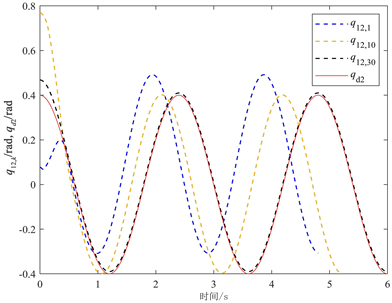
Figure 2. Joint position q_12,k and expected position signal q_d1

图2. 关节位置q_12,k和期望位置信号q_d2

Figure 3. Performance index

图3. 性能指标

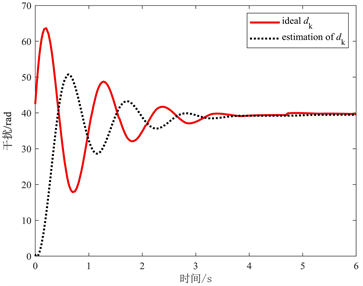
Figure 4. Approximation of d_k by the 30th iteration iteration RBF neural network

图4. 第30次迭代的RBF神经网络对d_k的逼近

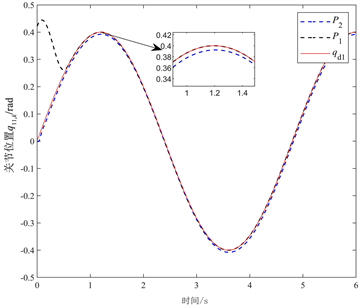
Figure 5. Joint position q_11,k tracking comparison

图5. 关节位置q_11,k跟踪对比

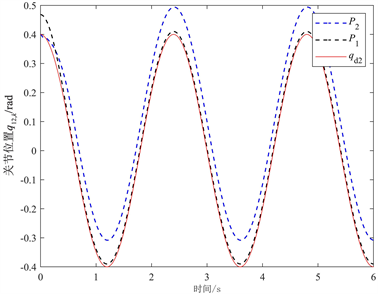
Figure 6. Joint position q_12,k tracking comparison

图6. 关节位置q_12,k跟踪对比

图1和图2分别表示机械臂系统的关节位置q_11,k和q_12,k对期望轨迹q_d1和q_d2的跟踪效果。由图1和图2可知，在任意初始状态下，经过足够多的迭代以后，本文所提的控制方法能够实现关节位置在指定区间跟踪期望轨迹，且在30次迭代之后，两个关节位置的跟踪精度均优于前面的跟踪精度。图1和图2还可以看出实际操作长度随迭代次数k随机变化的情况。图3描述了性能指标随迭代次数的变化趋势。随着迭代次数的增加，本文所提方法能够有效提高跟踪误差的收敛性能。通过图4可以看出RBF神经网络在T_max = 6 s时，基本可以完全跟踪到干扰d_k。图5和图6分别表示P1和P2两种控制方法下关节位置q_11,k和q_12,k对期望轨迹q_d1和q_d2的跟踪效果。由图5和图6可得，随着迭代次数k的增加，关节位置q_11,k和q_12,k对期望轨迹q_d1和q_d2的跟踪越来越精确。

6. 结论

基于RBF神经网络和迭代学习方法，本文解决了机械臂在任意初始状态下和迭代不等长的轨迹跟踪问题。针对机械臂系统的初始值问题，引入期望误差轨迹，使系统可在任意初始值时跟踪到期望轨迹。针对迭代过程不等长的问题，设计了虚拟控制器，使跟踪控制误差的收敛性也能在整个期望的迭代长度上得到保证。针对机械臂系统中的内外部干扰问题，采用RBF神经网络进行处理，提高跟踪的精确性。利用能量函数证明跟踪误差沿迭代轴渐近收敛到零，所提出新的迭代学习控制算法也可以解决传统的迭代学习控制问题。