基于时空的深度学习模型感知通行时间

Spatial-Temporal Based Deep Learning Model Perceives Travel Time

摘要: 随着国民经济的快速增长，人们的生活水平日益提高，私家车的数量不断增加，导致城市出现一系列交通拥堵问题和事故。因此，对于城市交通监控、导航、路线规划和乘车共享来说，感知给定城市路径的通行时间至关重要。以前的方法总是感知单个路径的通行时间，然后将它们相加为整个路径的通行时间。我们提出了一个基于时空的深度学习框架来感知整个路径的通行时间。更具体地说，我们使用卷积神经网络来捕获时间和空间依赖性。由于还有一些影响因素(如天气、时间、驾驶员等)影响通行时间，我们添加了一个影响因素模块来预处理数据。大量的实验证明，我们提出的模型显著优于其他已知模型。

Abstract: With the rapid growth of the national economy, people’s living standards are improving day by day, and the number of private cars is increasing, leading to a series of traffic congestion problems and accidents in cities. Therefore, it is essential for urban traffic monitoring, navigation, route planning, and ride sharing to perceive the travel time of a given urban path. Previous methods always perceived the travel time of a single path, and then summed them as the travel time of the whole path. We propose a spatial-temporal-based deep learning framework to perceive the travel time of the entire path. More specifically, we use this convolutional neural network to capture both temporal and spatial dependencies. Since there are also some impact factors (such as weather, time, driver, etc.) that affect the travel time, we have added an impact factor module to preprocess the data. Extensive experiments have shown that our proposed model is significantly outperforming other known models.

1. 引言

准确的到达时间评估有助于用户更好地搜索路线，避免拥堵；几乎所有的电子地图和出租车软件都提供通行时间感知；对个人而言，准确的通行时间感知可以帮助路上的人准确制定通行计划，避免浪费时间；对于打车软件/电子地图服务提供商来说，准确的出行时间感知可以帮助他们提高竞争力，改善和丰富运输服务的市场秩序；对于道路决策者来说，可以缓解关键地区的交通拥堵，避免打车难的问题，从而降低交通事故的发生率，促进智慧城市的建设。目前有两种主要的感知方法 [1] [2] [3] [4] ：基于个人的和基于集体的。前者累积道路每个路段的误差，不考虑路段之间的连通性。后者，随着轨迹的增加，将导致轨迹点稀疏的问题。

通行时间感知是智能交通系统(ITS)实施的重要组成部分，特别是对于高级通行者信息系统(ATIS)。ATIS是ITS的关键组成部分。它旨在使用一系列技术(如无线、电视、电话、互联网和车载动态导航系统)来满足乘客的信息需求，帮助他们做出更明智的出行决策，并减轻交通拥堵的影响。它可以向乘客提供目的地、路线、出发时间和其他信息。这些实时信息还可以帮助重新规划路线，以避免意外的交通拥堵。因此，研究通行时间感知具有重要的现实意义。通行时间感知是一项复杂而富有挑战性的任务。由于天气、路网交通状况和其他因素，通行时间通常在不同时间和不同交通状况下表现出强烈的波动。为了准确感知行程时间，通常需要上游和下游道路的数据。因为在拥堵的交通条件下，上游和下游车辆会对目标道路的行驶时间产生严重影响。因此，通行时间感知需要高度复杂的交通模型或能够从数据中提取交通模式的数据驱动模型。

在本文中，我们的方法主要有三个贡献，以解决先前通行时间感知中的问题。

1) 考虑影响通行时间的许多因素，这些因素是影响准确性的重要指标。

2) 对初始数据进行进一步处理，突出道路节点之间的空间相关性。

3) 时间序列数据感知方法更准确。

2. 相关工作

ARIMA [5] 获得的交通数据为城市出行时间感知提供了先进的模型和工具。使用数据驱动方法，在该方法的框架内测试不同的统计模型，其中对上述数据进行过滤、清理和融合，以更好地感知路线通行时间。所提出的方法已应用于罗马市：通过使用基于ARIMA的模型，在观察到的交通条件下获得了更好的性能。SARIMA [6] 模型是一个季节性时间序列模型，它源自ARIMA。它可以使用Box-Jenkins模型识别、预测和感知程序。此外，它主要用于分析季节性变化(包括年度、季度、月度、每周等)或其他因素导致的周期性变化的时间序列，并且可以很容易地利用先前的数据来获得对模型的实时调整。SARIMA是一个短期感知模型。核心点是对数据进行处理，并将六值拟合产生的误差作为分析元素。它的突出优点是短期感知结果具有更高的准确性，而相对缺点是模型对于长期感知的应用价值略低。此外，Ampountolas提出了SARIMAX [7] 模型，以适应不同的应用场景。时间序列法是一种基于分析时间序列之间的相关性，通过估计相关参数，使用历史数据来感知未来发展趋势的方法。与传统的时间序列方法相比，SARIMAX模型考虑了内生关系，然后分析了外部变量对拟合内容的影响，这大大提高了外部条件变化的拟合精度。

支持向量机(SVM) [8] 是一种新的学习机器。它具有很强的学习能力，泛化能力明显优于神经网络。很容易平衡拟合程度和泛化程度。SVM作为一种新兴技术，已经应用于通行时间感知。SVM基于统计学习，不需要特定的函数形式。此外，经过训练的SVM可以捕捉非线性系统的输出变量和输入变量之间的复杂关系。在感知模型构建方面，GPR (高斯过程回归)和KRR (核岭回归)被引入城市轨道交通的短期客流感知领域。基于GPR车辆流量感知，将GPR的感知结果、感知结果的方差估计、假日信息和站点类别信息相结合。采用KRR算法对GPR感知结果进行修正，有效提高了基于时间效率的感知精度。

交通流序列具有典型的时间序列特征。递归神经网络(RNN) [9] 、长短期记忆(LSTM) [10] 和门控递归单元(GRU) [11] 网络被应用于通行时间感知。LSTM和GRU算法可以增加时间序列的记忆功能，可以很好地传递车流历史数据的连续性，提取车流历史数据特征，并以5分钟的间隔感知未来24小时的车流。通过实验训练得到最优的循环神经网络结构，以解决短期车流预测问题。与单隐层结构相比，双隐藏层的LSTM和GRU误差减小，拟合优度提高。当数据波动较大时，具有双隐藏层的LSTM和GRU算法对于峰值感知不太准确，并且容易过度拟合。为了解决这一问题，利用综合熵权神经网络方法计算了每个算法的熵。根据整个系统中的信息量，通过熵权分布将LSTM和GRU算法相结合，得到了一种新的熵权分布算法。实验表明，基于熵权法的短时车流感知算法比单一的LSTM或GRU算法具有更高的精度和更小的误差。预测值更接近于波的峰值，对于感知波动更好。

T-GCN [12] 模型应用于基于城市道路网络的交通预测。T-GCN模型集成了图形卷积网络和门控递归单元。使用图卷积网络来捕获道路网络的拓扑，以对道路网络的空间相关性进行建模。T-GCN模型也可以应用于其他时空感知任务。T-GCN模型在不同的感知水平上是稳定的，表明T-GCN不仅可以用于短期感知，也可以用于长期交通感知任务。STGCN [13] 解决了穿透域中的时间序列预测问题，并使用纯卷积结构构建模型，这允许使用更少的参数进行更快的训练。此外，STGCN通过对多尺度交通网络进行建模，有效地捕捉了所有空间–时间连接，并始终保持各种真实世界交通数据集的SOTA。ASTGCN模型用于解决交通流感知问题。ASTGCN由三个主要的独立组件组成，它们对车辆流量的三个时间特性进行建模。对这三个分量的输出进行加权和融合，以产生最终的感知结果。PeMS的实验数据表明，所提出的ASTGCN优于STGCN模型。

我们提出了一种基于深度学习的模型 [14] [15] [16] [17]，以处理轨迹之间的时空依赖性和其他影响因素。该模型首先对轨迹点数据进行预处理，然后将天气、时间、驾驶员和其他因素链接到时间影响模块。然后，使用非线性函数将路径映射到网格，应用卷积神经网络从路径中的轨迹点提取空间特征，并使用TCN从路径的轨迹点中提取时间特征。最后，我们使用全连接层和Relu激活函数来处理输出结果，以获得最终的通行感知时间。

3. 模型设计

3.1. 概述

Figure 1. Structure diagram of DeepSTIF Model

图1. DeepSTIF模型结构图

本节概述了深度时空影响因子(称为DeepSTIF)模型的设计思想。DeepSTIF模型的详细结构如图1所示。详细描述了DeepSTIF模型中的影响因子模块(称为IFM)、时间特征提取模块(称为TFEM)和空间特征提取模块(称为TFEM)的计算过程和功能。

3.2. 影响因素模块

根据实际情况，当我们感知车辆的行驶时间时，需要考虑一些外部因素，例如天气、时间以及驾驶员对道路的熟悉程度。本文提出了一个影响因素模块(称为IFM)，以充分考虑这些外部因素。在该IFM中，使用非线性函数来权衡这些影响因素，并将其输出到时间特征提取模块。

$Result=Connect\left(Q_{time}\oplus Q_{weather}\oplus Q_{driver}\right)$ (1)

在公式(1)中， $Q_{time}$ 表示时间影响因素， $Q_{weather}$ 表示天气影响因素， $Q_{driver}$ 表示驾驶员影响因素， $\oplus$ 表示加权操作，Connect表示连接操作。输出向量Result用作时间特征提取模块的输入。

3.3. 空间特征提取模块

为了更好地提取空间和地理位置之间的相关性，我们提出了一种新的空间特征提取模块(称为SFEM)，如图2所示。首先，通过公式(2)将轨迹上的每个点映射到12维空间。

$Lo{c}_i=Tanh\left(W_{loc}\ast \left[P_i\cdot lat\divideontimes P_i\cdot lng\right]\right)$ (2)

然后对得到的 $Lo{c}_i$ 进行卷积，每个卷积产生如下向量列表：

$Lo{c}_i^{con}={\rho }_{cnn}\left(W_{con}\ast lo{c}_{i:i+t-1}+a\right)$ (3)

地理特征的最终输出通过使用以下公式将一列距离向量拼接到卷积向量上来获得：

${\displaystyle {\sum }_{n=i+1}^{i+t-1}Dis\left(P_{n-1},P_n\right)}$ (4)

最终的地理特征记录为 $Lo{c}^f$ ，也用作时间特征提取模块的输入。

Figure 2. Structure diagram of SFEM

图2. SFEM模块结构图

3.4. 时间特征提取模块

如图3所示，我们为本文设计的四维数据结构创建了一个新的时间特征提取模块(TFEM)，以计算数据时间相关性的特征。以下三个因素主要突出了TFEM的作用：首先，它跟踪所有历史数据，并使用因果卷积计算长期历史数据。其次，它采用空洞卷积来增加卷积过程的感受野。为了防止在深度计算过程中由于感受野过宽而导致的局部信息丢失，空隙因子在凸函数下进行调整。最后，它使用多层残差结构代替传统的递归神经网络选通结构，并且完全由卷积网络构成。它击败了标准递归神经网络缓慢的训练速度和无法处理并行计算的缺点。

Figure 3. Structure diagram of TFEM

图3. TFEM模块结构图

3.4.1. 因果卷积

为了进一步回溯时间并重建历史数据，因果卷积是一个应用的概念。因果卷积公式见(5)。 $\left\{x_1,x_2,\cdots ,x_t\right\}$ 是输入序列， $\left\{y_1,y_2,\cdots ,y_t\right\}$ 是隐藏层输出序列，而 $\left\{f_1,f_2,\cdots ,f_k\right\}$ 表示滤波器。因果卷积排除了未来的知识，只关注过去。只有 $x_t$ 之前的信息才能用于确定 $y_t$ 的结果。可以跟踪的历史数据越多，K越高。如果当前层的初始输入序列为[0, i]，则下一层的初始输出序列将为[0、i + 1]。

$y_t={\displaystyle {\sum }_{i=1}^K{f}_i\cdot x_{i-K+1}}$ (5)

3.4.2. 空洞卷积

深度网络的模型 [18] [19] [20] [21] 必须始终进行下采样，以扩大接收范围并减轻计算负担。通过这样做，即使可以扩大感受野，空间分辨率也会降低。空洞卷积是一种技术，可用于增加感受野而不牺牲分辨率。空洞卷积有一个参数，可用于设置分割率。应用不同的分割率，感受野将不同，从而获得多尺度信息。空洞卷积公式如(6)所示。

$y_t={\displaystyle {\sum }_{i=0}^{K-1}{f}_i\cdot x_{t-i\cdot d}}$ (6)

d表示空隙系数，其将根据网络深度根据凸函数2变化。增加d或k可以增加感受野的范围。局部信息的丢失发生在深度网络中，在那里，随着网络层的加深，感受野使得来自长距离卷积的信息变得毫无意义。因此，我们根据2的指数函数改变空隙系数，如图3中d的变化过程所示。这种设计模式确保了深度网络的感受野的深度在一定程度上受到限制，从而最大限度地减少了本地信息的损失。神经元密集的信息传输也提高了模型在深层特征计算过程中的准确性。

3.4.3. 残差结构

Figure 4. Multilayer residual structure

图4. 多层残差结构图

如图4所示，在传统递归神经网络中使用残差结构 [22] [23] [24] 代替门控结构，以简化训练过程的复杂性。残差结构的基本组成部分是两层卷积网络和非线性映射过程。权重范数是一种使用重参数化权重归一化对数据进行归一化的方法。权重范数经常被用来加速模型收敛。通过调整权重，可以在梯度旋转期间抑制梯度范围，并且可以实现梯度的自稳定。

本实验中使用的城市交通韧性指数数据的取值范围为[0, 1]。加载数据后，Z-Score被标准化，公式如下：

$Z=\frac{x-\bar{x}}{S}$ (7)

x是原始数据， $\bar{x}$ 是平均值，S是标准差。从Z-Score的计算中可以看出，由于原始数据与平均值( $x-\bar{x}$ )之间的关系在计算过程中保持不变，因此平均值的Z-Score等于0，其他值的Z-Score在大于平均值时为正值，而在小于平均值时则为负值。数据标准化后，城市交通韧性指数的最小值和最大值分别为−2.399和1.415。提高训练效率的理想0均值是tanh函数。由于tanh的输出是区间[−1, 1]，因此参数的梯度值在训练过程中具有异常符号，使得在更新时很难出现锯齿现象，从而很容易达到理想值。

3.5. 后处理

基于上述加权范数理论，我们将批处理范数添加到数据规范化过程中，以处理激活时间特征提取模块后由于数据量过大而导致的网络性能不稳定。批次标准层的公式如(8)所示：

$y=\frac{x-m}{\sqrt{s}+\delta }\times \alpha +\beta$ (8)

其中m是输入数据的平均值，s是输入数据方差， $\delta$ 是用于提高计算稳定性的稳定性因子。其值等于1e−5。 $\alpha$ 和 $\beta$ 是系数矩阵。数据的归一化可以通过在垂直于空间轮廓的方向上倾斜梯度下降来提高模型的收敛速度。它还可以通过平均特征计算中使用的每一级数据的权重来提高模型的正确性。网络的分散特征最终通过整个连接层映射到样本目标空间。

4. 实验

4.1. 数据集介绍

a) 上海数据集：包含13,658辆出租车的3,615,176条行动轨迹，其中最短路径仅包含15个GPS点(2.4 km)，最长路径包含161个GPS点。

b) 北京数据集：包括20,156辆出租车的5,416,329条行动轨迹，其中最短路径包括18个GPS点(3.2 km)，最长路径包括185个GPS点。

4.2. 基准线

传统的递归神经网络、时空神经网络和图形时空神经网络是我们为评估模型性能而创建的三种基线。相同的数据集用于训练和评估所有模型。大量训练和评估结果的平均值是实验结果。不同基线的实验模型结构如下：

LSTM：通过门控机制，它调节数据传输状态。与普通的RNN只机械地叠加一种记忆相比，LSTM的原理是保留需要长时间记忆的信息，忘记不重要的信息。

GRU：它的输入和输出结构与标准RNN相当，其处理逻辑与LSTM相当。与LSTM相比，GRU具有比LSTM更少的“门控”和更少的参数，但它可以实现与LSTM相同的功能和精度。考虑到硬件的计算能力和时间成本，GRU是更多从事深度学习的研究人员的选择。

GCN：为了创建新的特征表示，使用过滤器完成空间区域中的加权像素求和。卷积核的参数是加权系数。

T-GCN：该方法将图卷积网络(GCN)与门控递归单元(GRU)相结合，GCN用于学习复杂拓扑以捕获空间相关性，GRU用于学习交通数据的动态变化以捕获时间相关性。

STGCN：它使用连续的三层卷积网络和一层GCN来形成时空卷积块(ST卷积块)，并使用两层ST卷积块来处理数据。

ASTGCN：它使用两层时空块ST block来处理数据，每一层都有一个空间和时间关注层。最终，它完成了一个具有三个时间特征并完全集成的过程。

DeepTTE：目前，它是一个很好的道路通行时间感知模型。对原始GPS轨迹信息进行非线性映射，然后使用CNN和LSTM提取每条路线的时空特征。

4.3. 评估指标

在本实验中，使用两个指标来评估模型的性能，包括均方根误差(RMSE)和平均绝对误差(MAE)，计算公式如下所示。

$\text{RMSE}=\sqrt{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\left({\hat{y}}_i-y_i\right)}^2}}$ (9)

$\text{MAE}=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n\left|{\hat{y}}_i-y_i\right|}$ (10)

模型感知的准确性可以通过MAE测量，然而，所有计算都基于绝对误差。虽然绝对误差可以提供一个评估值，但我们无法确定该评估值代表的模型执行情况。我们只能通过比较现有模型来确定最佳模型。因此，RMSE也被用于实验的评估过程。RMSE用于量化实际值和预测值之间的差异，它对数据收集中的非常大和非常小的错误都很敏感。因此，RMSE可以准确地反映感知结果的准确性。

4.4. 实验设置

前一周的数据用于训练，而其他数据用于训练过程中的评估。每个训练过程有200轮，每个训练过程50个时隙。超参数的初始值设置为1，初始学习率(LR)设置为0.001，并且在训练期间选择Adam优化作为梯度优化器。

4.5. 实验结果

已经进行了大量实验，以评估DeepSTIF在真实轨迹数据集上的性能。在训练阶段，使用MAE和RMSE两个评估指标来评估感知结果。实验结果如表1所示。

Table 1. Performance comparison of different approaches on the Beijing Dataset

表1. 北京数据集上不同方法的性能比较

当使用LSTM方法进行感知时，误差较大，精度相对较低。GCN是通过滤波器对空间区域中的像素进行加权求和以获得新的特征表示。GCN的感知精度显著高于LSTM，但在处理数据时忽略了数据之间的时间相关性，导致实验结果不佳。T-GCN将图卷积网络和门控递归单元集成到STGCN中，并使用纯卷积结构来构建模型，这允许使用更少的参数进行更快的训练。同时，STGCN通过对多尺度交通网络进行建模，有效地捕捉了所有时空相关性，并且在感知方面优于T-GCN。ASTGCN由三个主要的独立组件组成，它们模拟了交通流的三倍特性。对这三个分量的输出进行加权和融合，以产生最终的感知结果。结果远远优于以前的GCN模型。DeepTTE是一种端到端的方法，它同时考虑了时间和空间依赖性，性能比GCN好得多。最后，测试结果表明，我们的DeepSTIF模型优于任何其他模型。图5显示了实验结果。

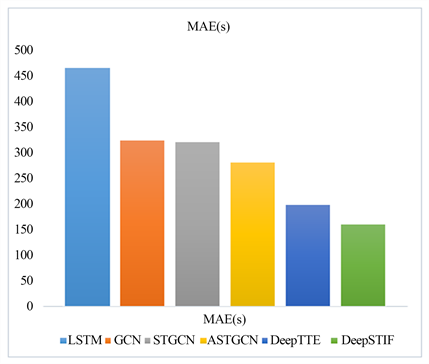
Figure 5. Experimental results of different evaluation indicators

图5. 不同评估指标下的实验结果

为了进一步研究模型的各个部分对感知结果的影响，我们进行了大量实验。在IFM中，为了更好地捕捉道路的特征信息，我们分别研究了出发时间和天气影响因素对时间感知的影响，结果如图6所示。在DeepSTIF模型中，通过添加出发时间和天气属性，MAE分别减少了157.69秒和134.67秒。当添加两个属性时，MAE减少216.54 s。RMSE显示相同的结果。实验结果证明了这两个属性的有效性。这符合这样一个现实，即当您的出发时间与通勤者的高峰时间重合时，道路上的车辆数量将急剧增加，相应的交通时间将更长。在大雨或雾天，司机会减速以确保安全，车辆的通行时间自然会相对较长。因此，当出发时间和天气影响因素被添加到道路的特征信息时，当前道路的预测通过时间的准确性被大大提高。

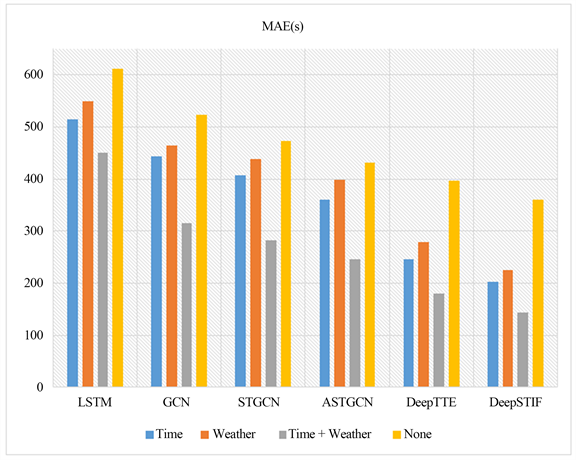
Figure 6. Changes in MPE Indicators when adding weather and time attributes

图6. 当增加天气和时间变量后MPE指标的变化

5. 结论

为了准确地感知车辆在城市道路上的行驶时间，我们提出了一个DeepSTIF模型来处理轨迹之间的空间依赖性、时间依赖性和其他影响因素。在SFEM中，模型首先对轨迹点数据进行预处理，然后将天气、时间、驾驶员和其他因素连接起来输出到TFEM。然后，使用非线性函数设置网络路径，通过CNN从点的路径中提取空间特征，并通过TCN从点的轨迹中提取时间特征。最后，我们使用全连接层和Relu激活函数来处理TFEM输出，以获得最终的通行感知时间。最后，我们比较了DeepSTIF与LSTM、GCN和DeepTTE的感知效果。实验表明，我们的模型对城市道路上的车辆行驶时间具有良好的感知性能。

基金项目

本研究得到国家重点研发计划重点专项项目(2018YFB2100303)、山东省高校青年创新科技计划创新团队项目(2020KJN011)、山东省自然科学基金项目(ZR2020MF060)的部分资助。山东省创新型博士后人才资助号40618030001，国家自然科学基金资助号61802216，国家博士后科学基金资助号2018M642613。

NOTES

^*通讯作者。