1. 引言
随着工业技术的进步,工业上要求机器人的运行轨迹的精度越来越高,执行速度也越来越快 [1]。实现机器人高精度高速度的运行轨迹的重要一个步骤就是建立精确的动力学模型 [2]。机器人的几何尺寸可以通过直接测量获得,但是对于一些动力学参数,无法通过测量直接获得 [3]。因此,对工业机器人动力学参数进行辨识是必不可少的一步。
测量机器人动力学参数方法有三种,分别是解体测量法,CAD法和整体辨识法 [4]。由于需要考虑机器人实际运行中的装配关系和材料属性,解体测量法和CAD法往往导致测量结果的不精确,而整体辨识法可以考虑机器人的实际运行情况 [4] [5],具有更高的辨识精度。因此本文采用整体辨识法进行动力学参数辨识。
机器人动力学参数辨识的步骤一般包括推导动力学模型及线性化处理、激励轨迹的选取和优化、数据采集与处理、参数估计和误差对比 [6]。国内外学者对机器人动力学参数辨识已经做了一些系统性的研究。Gautier [7] [8] 为了获得精确的动力学参数,采用卡尔曼滤波处理数据并根据最小二乘算法对机器人的动力学参数进行估计。Atkeson [9] 使用五次多项式作为机器人的激励轨迹并采用最小二乘辨识算法进行参数估计,获得了不错的辨识结果。Swevers [10] 第一次提出使用周期性傅里叶级数作为机器人的激励轨迹,取代了多项式形式的激励轨迹,并迅速被广泛应用。丁亚东等 [11] 将参数辨识分成多个步骤,多次辨识得到动力学参数,虽然可以准确地辨识出动力学参数,但是辨识过程过于复杂。刘勇 [12] 根据智能算法,利用多目标粒子群优化算法对机器人的关节轨迹进行优化,并取得了良好的效果。吴文祥 [13] 等采用最大似然估计方法对机器人的动力学参数进行估计,也取得了较好的精度效果。
本文根据Lagrange方程建立ABB-IRB2600型机器人前三轴的动力学方程,用傅里叶级数作为激励轨迹并对激励轨迹系数进行优化 [14] [15]。将激励轨迹导入到ADAMS动力学仿真平台进行仿真实验并得到了相关数据,最后根据最小二乘法计算出机器人的动力学参数。
2. 动力学模型的建立
Newton-Euler法和Lagrange法是推导机器人的动力学方程两种常用方法。其中Newton-Euler法是基于各杆件的内力关系通过正向递推和逆向递推建立机器人动力学模型 [16] [17]。Lagrange法是从能量的角度出发,计算机器人关节运动的动势能,从而推出动力学模型 [16]。
2.1. 动力学模型推导
ABB-IRB2600机器人是典型的六轴关节型机器人,一般用于物料搬运、机器上下料、点焊、弧焊、切割、装配、测试、检测、涂胶、研磨和抛光等方面。如图1所示是ABB-IRB2600机器人。
本文用Lagrange方程建立机器人前三关节的动力学的模型,主要对前三关节进行参数辨识,建立动力学方程如下:
(1)
其中,
表示关节力矩,
表示关节角度,
表示关节角速度,
表示关节角加速度,
表示惯性矩阵,
表示科里奥利和离心力,
表示重力项。
由于机器人关节摩擦力是一个比较复杂的非线性模型,本文采用库伦摩擦+粘性摩擦的形式来对机器人关节摩擦进行建模 [18],形式如下所示:
(2)
其中,
是关节摩擦力矩,
是关节粘性摩擦系数,
是关节库伦摩擦系数,sgn是符号函数。
因此,机器人动力学方程可以表示为:
(3)
根据文献 [19],机器人的动能与势能为机器人惯性参数的线性形式,故
,
,
,
满足如下线性关系:
(4)
其中,
表示机器人观察矩阵,
表示机器人待辨识的动力学参数,且机器人单个臂杆i的动力学参数可表示如下形式:
(5)
其中,
表示连杆i的惯性张量,
表示连杆i的一阶质量矩,
是连杆i的质心。
2.2. 动力学参数重组
由于观察矩阵
是一个非满秩矩阵,因此必须对其进行处理获得一组最小惯性参数,这组最小惯性参数一方面要保证数量最小,另一方面要保证每个参数对机器人的动力学特性有影响。根据文献 [19] 的方法,通过机器人动力学参数重组可以计算出这组最小惯性参数,具体方法可以参考文献 [19]。经过重组后共有21个待辨识的动力学参数,其动力学模型可以表示为如下形式:
(6)
其中,
为观测矩阵,
为机器人动力学最小惯性参数也是待辨识的动力学参数。
式中:
且,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
3. 激励轨迹优化设计
激励轨迹的设计是机器人动力学参数辨识的重要步骤,对机器人动力学参数辨识的精度尤其重要。激励轨迹的设计可分为激励轨迹的选择和激励轨迹系数的优化两个部分。本文选用傅里叶级数作为机器人的激励轨迹。
3.1. 傅里叶级数激励轨迹
傅里叶级数激励轨迹模型如式(7)所示:
(7)
式中:i表示机器人的关节数;
l表示采用的傅里叶级数的阶数;
N表示傅里叶级数的谐波项数。
选取N = 5,因此机器人每个关节的傅里叶级数有
个待优化的参数,
表示基频,
表示频率,
,
和
表示傅里叶级数系数,
表示偏移量,
,
,
表示待优化的激励轨迹系数。
3.2. 激励轨迹系数优化
关于机器人激励轨迹的优化有多种优化标准,其中使用最多的优化标准是条件数法。因此本文采用条件数法,在优化过程中,条件数越小,机器人在各关节约束范围内的动力学特性就发挥的更充分,自身误差带来的干扰就越小,参数辨识结果就更精确。
3.2.1. 目标函数
定义条件数作为目标函数:
(8)
式中:
表示观测矩阵W奇异值最大值;
表示观测矩阵W奇异值最小值;
的表达式为
。
矩阵W是每个采样点对应的所有观测矩阵的集合阵:其矩阵大小为
,其中
为采样点数,3为机器人前三关节个数,
为待辨识动力学参数集维数。
3.2.2. 约束条件
定义各关节的约束条件为:
(9)
表1表示机器人各关节具体约束大小:
根据傅里叶级数激励轨迹的数学模型,将式(7)代入到式(9)并化简后得优化参数
的非线性不等式约束关系 [20] :
(10)
除此之外,设置关节角度、关节角速度和关节角加速度初始值为0,
的非线性等式约束条件为:
(11)
3.2.3. Fmincon函数优化
本文采用MATLAB优化工具箱中的Fmincon函数对机器人的激励轨迹系数进行优化。下式表示Fmincon函数的详细说明:
(12)
式中:
代表非线性不等式约束;
代表非线性等式约束;
代表线性不等式约束;
为线性等式约束;
为待优化参数的上下限。
Fmincon函数的基本形式如下:
(13)
其中,fun为目标函数,后面的nonlcon为非线性约束(包括等式和不等式);x0表示决策变量的初始值,可以随机取一组符合约束条件的数据值;A,b,Aeq,beq分别表示线性不等式约束和等式约束。关于Fmincon函数的详情可见MATLAB帮助文档。
将观测矩阵的条件数作为目标函数,根据各关节得到约束条件,用Fmincon函数对机器人的激励轨迹系数进行优化,优化后的最小条件数大小为cond(W) = 51.5,最优的激励轨迹系数如表2所示:

Table 2. Optimization results of excitation trajectories of each joint
表2. 各关节激励轨迹优化结果
机器人最优激励轨迹曲线如图2~4所示,由图中可知优化后的各关节激励轨迹都在约束的范围之内,并且优化后的激励轨迹所对应的观测矩阵条件数最小,可以充分地激发机器人的动力学特性,降低观测矩阵自身带来的计算误差,提高动力学参数的辨识精度。
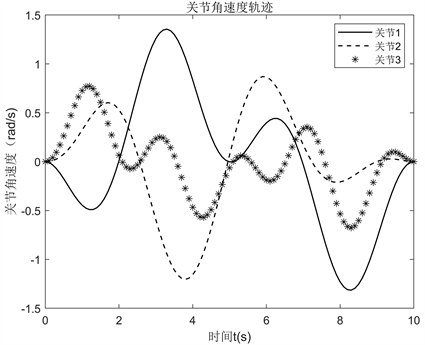
Figure 3. Joint angular velocity trajectories
图3. 关节角速度轨迹
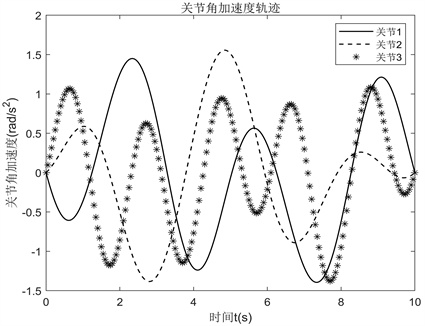
Figure 4. Joint angular acceleration trajectories
图4. 关节角加速度轨迹
4. 采样数据处理与参数估计
4.1. 采样数据处理
将最优激励轨迹输入到ADAMS仿真软件中,使机器人在ADAMS中运行最优激励轨迹,并测量各关节的角度和力矩数据,多次重复运行激励轨迹,并求取多次测量数据的均值以便于后续的计算。将测量得到的关节力矩和关节角度进行滤波处理和关节角度数据的差分运算,最终得到仿真过程中的力矩,角度,角速度及角加速度数据。
4.2. 最小二乘估计算法
当采集完数据后需要进行机器人的参数估计,现已有多种算法可进行参数估计,本文用最小二乘法进行动力学参数的估计。
对于如下模型,如果定义:
(14)
(15)
(16)
在式中,
代表待估计的参数。
若令
,则有:
(17)
(18)
(19)
(20)
故:
(21)
最小二乘算法的原理就是找到一个
的估计值
,使得各次测量的
与由估计
所确定的
之差的平方和最小,即:
(22)
(23)
(24)
如果
的行数大于等于列数,即
,并且
满秩,即
,则
存在。因此
的最小二乘估计为:
(25)
5. 仿真实验与结果分析
本文通过ADAMS动力学分析软件对机器人进行仿真实验,并借助MATLAB对数据进行处理,以验证上述理论的正确性。仿真过程中用到的机器人模型与实际机器人实体一致,实验步骤如下:
步骤一:动力学参数辨识实验仿真。将优化后的激励轨迹导入到ADAMS软件中,如图5所示,并定义机器人各杆件理论惯性参数等属性,使机器人运行最优激励轨迹,测量关节力矩和角度数据。
步骤二:数据处理。对测量得到的关节力矩和关节角度进行滤波处理和角度的差分运算,计算出关节角速度和角加速度数据。
步骤三:动力学参数辨识。将测量和计算得到数据代入机器人动力学方程,并根据最小二乘法计算机器人动力学参数。
步骤四:验证与分析。将机器人理论惯性参数值与本文辨识算法计算的惯性参数值作比较并计算绝对误差,以验证参数辨识的准确性。
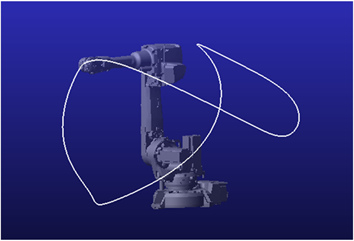
Figure 5. The motion path under the robot excitation trajectory
图5. 机器人激励轨迹下的运动路径
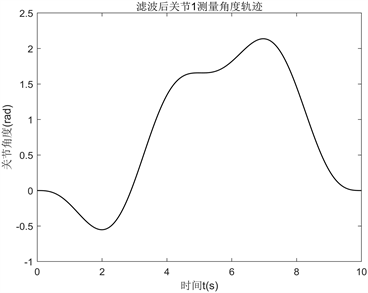
Figure 6. Joint 1 after filtering measures the angle
图6. 滤波后关节1的测量角度
Figure 7. Joint 2 after filtering measures the angle
图7. 滤波后关节2的测量角度
Figure 8. Joint 3 after filtering measures the angle
图8. 滤波后关节3的测量角度
图6~8分别是滤波后得到的各关节角度数据,图9~11分别是滤波后得到的各关节力矩数据。最后将处理后的数据代入到最小二乘辨识算法中进行参数估计,最终得到机器人的动力学参数值如表3所示:

Table 3. Dynamic inertial parameter identification results
表3. 动力学惯性参数辨识结果
如表3的第4列所示是机器人的理论惯性参数和辨识算法计算得到的惯性参数的绝对误差,其绝对误差较小,由此可以证明本文的辨识算法的正确性。
6. 总结
1) 由Lagrange法推导工业机器人前三关节的动力学方程,处理方程得到待辨识的动力学参数。
2) 选用傅里叶级数作为机器人激励轨迹,并借助MATLAB的优化工具箱对机器人的激励轨迹进行优化,最终得到一组最优激励轨迹。
3) 将优化后的最优激励轨迹导入到动力学仿真软件中,使机器人运行最优激励轨迹,测量关节角度和关节力矩,并进行数据处理,将处理得到的数据代入机器人动力学方程,并根据最小二乘法计算机器人动力学参数。
4) 将计算值与理论值进行对比。结果表明:理论值与辨识值绝对误差较小,证明本文辨识方法的正确性和有效性,为机器人实际动力学参数辨识提供了参考依据。