基于泰森多边形的仿生多孔结构设计方法

Biomimetic Porous Structure Design Method Based on Voronoi Diagram

摘要: 本研究采用泰森多边形原理设计了仿生多孔结构，利用参数化方法获得了联通多孔模型，实现了与骨缺损形状匹配的自由几何构造。与此同时，围绕孔隙率、孔径、孔棱直径、比表面积四个参数开展了设计参数与几何参数之间的关联探究，为实际工程应用提供了一定的理论依据。基于该方法生成的不规则多孔模型可通过增材制造、立体成像等技术进行3D打印。

Abstract: In this study, the Voronoi Diagram principle was used to design a bionic porous structure, and a parametric method was used to obtain a linked porous model to achieve a free geometric configura-tion matching the shape of the bone defect. At the same time, the correlation between the design parameters and geometric parameters was explored around four parameters: porosity, pore diam-eter, pore prism diameter, and specific surface area, which provided some theoretical basis for practical engineering applications. The irregular porous models generated based on this method can be 3D printed by additive manufacturing and stereo imaging technologies.

1. 引言

骨组织工程旨在研发出可在体内整合和降解的生物功能组织，实现受损或病变的组织修复和再生 [1]。如今，人工合成支架正在逐步取代自体移植或异体移植的骨修复 [2]。得益于我国庞大的人口基数、社会老龄化进程加速以及医疗需求不断上涨，骨科行业持续景气，预计到2024年全球生物材料和器件市场规模将超过5945亿美元，且复合年增长率(CAGR)约为5.6% [3]。先前的研究表明，最优的多孔植入物应当在机械性能、生物响应等方面尽可能的接近自然骨的水平，以便获得相似的细胞渗透、营养扩散以及生物降解的特性 [4]。

多孔植入物的设计必须要满足多个条件，从宏观上来说，其整体尺寸和轮廓必须要与患者的受损病变区域相匹配 [5] ；就微观而言，其内部多孔结构必须有利于间充质细胞的黏附、聚集、增殖，承担起相应的机械性能和生物响应作用 [6] [7]。通常对于人的骨头而言，松质骨的孔隙率在50%~90%之间，皮质骨的孔隙率则在10%左右 [8] [9]。与此同时，孔径尺寸应保持在200~1000 µm的范围内 [10] [11] [12] [13]。多孔结构的诸多特征参数对骨再生的时间和质量均有影响 [14]，此外，不同部位和位置的骨，其微观几何结构存在差异，因此要求设计过程中多孔植入物的孔隙率、孔径等参数必须可控 [15] [16] [17]。

当前多孔植入物的主流设计方法分为两个思路，其一是进行规则多孔结构设计，包含基本单元法 [18] 、极小曲面法 [19] 、拓扑优化法 [20] 等，将基本胞元进行阵列分布构建多孔模型，能够快速预测和控制模型的几何参数和力学性能，但难以兼顾低弹性模量和高强度的要求；其二是不规则多孔结构设计，包含逆向建模法 [21] 、数学建模法 [22] 等，逆向法能够有效地重现骨小梁结构，但是数据庞大且处理耗时，数模建模法则基于随机算法、分形理论等进行了仿生设计，虽能够较好地模仿自然骨结构，但却难以实现几何参数的可控。

为了克服这些限制，本文提出了一种基于Voronoi的数学建模法，以参数化设计手段为基础，生成不规则仿生多孔结构。该设计方法可通过输入特定的几何轮廓获得相应的多孔植入物模型，并支持交互修改特定的控制参数，实现微观几何结构的优化调整。本文将围绕不规则多孔结构的设计原理、整体工作流程及其对应的参数控制方法进行展开。

2. 方法

2.1. 泰森多边形原理

泰森多边形的结构在自然界中广泛存在，如长颈鹿身上的纹路、堆叠的肥皂泡泡、蜻蜓的翅膀、树叶的叶脉等，从宏观图案到微观结构，无处不在，是一种基于自然演化而存在的形态学逻辑规则。鉴于其在空间划分上的等分特性，被广泛应用于解决最近点、最小封闭圆等诸多问题，以及众多的空间分析问题，比如接近度、可达性分析等。

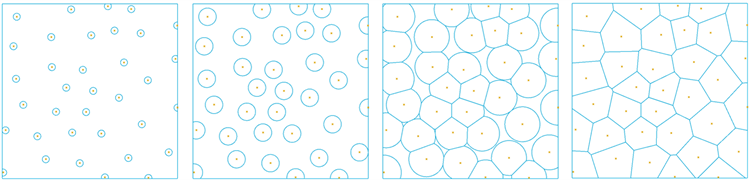
Figure 1. Cell/Voronoi diagram evolution process

图1. 细胞/泰森多边形演变过程

泰森多边形的生成与细胞的生长进化存在共通之处。如图1所示，起初细胞的存在模式为裂变后随机散布的小尺寸细胞；经历营养吸收等过程后，细胞尺寸逐渐增加，变为原有大小的几倍、几十倍；达到一定规模后，细胞便会在功能和结构上开始发生细胞特化，倘若仅考虑结构变化，则对于有限的细胞增殖空间而言，细胞尺寸的增长势必会导致相邻细胞的相互挤压，其结构会从原先的圆球状演变为由细胞间挤压面组合而成的多面体状，三维泰森多面体结构如图2所示。该过程反映了自然界的生长规则，生命的形态由内部向外扩张，由生长力量和限制性的外部力量共同决定的。因此，利用泰森多边形的原理进行骨结构的仿生构建具有一定理论依据的，也是相较而言最接近实际情况的一种模拟设计。

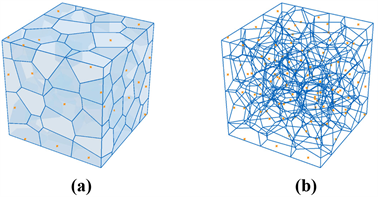
Figure 2. 3D Voronoi structure (a); Voronoi segmentation; (b) Wireframe structure

图2. 三维多面体结构 (a) 泰森分割；(b) 线框结构

对于s维欧氏空间 $R^s$ 中的一个离散点集P_t：

$P_t=\left\{p_{t1},\mathrm{...},p_{tn}\right\}\subset R^s,2\le n<\infty ,p_{ti}\ne p_{tj},i,j\subset I_n=\left\{1,\mathrm{...},n\right\}$ (1)

其中，任意种子点 $p_{ti}$ 和邻近种子点 $p_{tj}$ 所组成的连线 $p_{ti}{p}_{tj}$ ，其垂直平分面(超平面)将空间(超空间)分为两部分， $Q_i\left(p_{ti}{p}_{tj}\right)$ 表示点 $p_{ti}$ 一侧的空间，则 $R^s$ 空间中关于点 $p_{ti}$ 的s维Voronoi-Tessellation多面体 $Vor\left(p_{ti}\right)$ 以及由点集P_t生成的s维Voronoi-Tessellation集合 $\gamma \left(p_t\right)$ 可以表示为：

$Vor\left(p_{ti}\right)=\left\{x|\Vert x-p_{ti}\Vert \le |\Vert x-p_{tj}\Vert \right\}={\displaystyle \underset{j\in I_n/\left\{i\right\}}{\cap }Q}\left(p_{ti},p_{tj}\right)$ (2)

$\gamma \left(p_t\right)=\left\{Vor\left(p_{ti}\right),\mathrm{...},Vor\left(p_{tn}\right)\right\}$ (3)

由其生成机理和数学定义可知，多边形/多面体的形貌主要受种子点数量及其空间分布影响。对于空间位置确定的离散点集，泰森多面体的结构是唯一确定的，以此为导向深入研究，能够更好地实现不规则多孔模型的生成和调控。

2.2. 不规则多孔模型生成

在本章节中，借助三维建模软件Rhino7及参数化设计插件Grasshopper，提出了一个生成式设计工作流程，实现了三维泰森多面体的结构生成，用于骨科植入物的不均匀多孔模型构建，如图3所示。

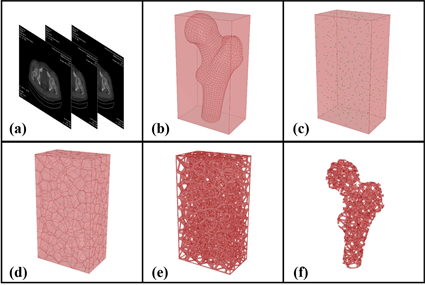
Figure 3. Diagram of orthopaedic implant generation.(a) CT image; (b) Design space; (c) Random points; (d) Voronoi segmentation; (e) Connected porous; (f) Boolean intersection

图3. 骨科植入物生成示意图 (a) CT图像；(b) 设计空间；(c) 随机点；(d) 泰森分割；(e) 开孔多孔；(f) 布尔交集

在生成流程中，输入模块及其对应的数据主要分为三部分：a) 设计空间，由患者受损或病变骨的CT图像重构获得；b) 随机点数量，空间中随机分布的种子点是实现泰森分割的依据，其数量也代表着分割后形成的泰森胞元数，是控制模型特征参数的重要设计指标之一；c) 缩放系数，被定义为空间中任意一点缩放后到缩放中心的距离与初始距离的比值，是梯度设计过程中最为关键的参数。对于开孔的不规则多孔模型而言，其设计主要分为四步走：

1) 实心泰森多面体。通过CT图像重构获得骨骼的几何轮廓，以其最小外接立方体作为设计空间，随机生成N个均匀分布的点。基于随机点集进行泰森分割，得到N个泰森多面体胞元。

2) 闭孔多孔模型。对于每一个胞元进行单独操作，以其质心进行体缩放，缩放系数为K，将初始胞元和缩放后的胞元进行布尔差分运算，即可得到闭孔泰森多面体胞元。

3) 开孔多孔模型。首先，以缩放后的泰森多面体胞元为基础，选取各缩放面质心为基准点，其次，以初始的泰森多面体胞元为基础，选取各面质心为目标点，将两组点按照面所对应的缩放关系依次连接形成向量，最后，基于该向量以及缩放后的面进行拉伸，对镂空胞元做切除处理，即可得到开孔泰森多面体胞元。

4) 定制模型。将获得的开孔泰森多面体胞元与患者骨骼几何轮廓做布尔交集运算，即可得到尺寸与之相匹配的骨科植入物模型。

模型的设计工作流如图4所示，其中蓝色模块为开展骨植入物时拟定的设计目标，绿色模块为生成软件中最重要的三大输入模块，白色模块为具体操作，红色模块为最终输出结果。由该工作流可知，模型的宏观结构由骨扫描数据重构后几何轮廓决定，而其内部微观构造则可通过泰森分割的种子点数量以及缩放系数进行调控。下一章节将基于生成的不规则多孔模型开展几何特征参数探究，分析孔隙率、孔径、孔棱直径、比表面积在设计过程中的可控性以及与设计参数之间的相关性。

Figure 4. Design workflow

图4. 设计工作流程

3. 结果

3.1. 孔隙率

多孔材料一般为气固两相组成的复合材料，而孔隙率则是用来衡量材料中气相体积占两相体积之和的比值，是决定材料力学、热学、光学及声学等诸多性能的关键参数。对于多孔植入物而言，随着孔隙率的提升，整体结构的弹性模量和极限抗压能力会逐渐降低，以自然骨的弹性模量为设计目标，通过对参数进行合理调控，可实现减轻应力屏蔽现象的效果。

对于均质多孔而言，材料的宏观孔隙率和微观孔隙率一致，但对梯度多孔而言，宏观孔隙率取决于内部的微孔结构，是所有微孔孔隙率的加权平均值，且权重为微孔的体积。

结合对宏观、微观孔隙率的思考，只需确保微孔结构在形成过程中的孔隙率可控即可实现宏观孔隙率的可控。因此，对模型进行离散化处理，以任意泰森多面体胞元为研究对象，分析其形成过程中的形体变化即可得到控制方法。回顾模型的生成，必须经历分割、镂空、开孔三个阶段，而孔隙率的关键在于体积的运算，故按照生成步骤依次计算各部分体积即可得到对应关系。假定某一实体胞元的体积为 $V_s$ ，则：

$V_c=K^3{V}_s$ (4)

其中， $V_c$ 为实体胞元缩放后的体积，即形成闭孔所需切除的体积， $K$ 为缩放系数。

借鉴任意多面体内切球半径的计算方法进行向量长度和开孔体积计算，以内切球球心为中心进行分割，生成若干底面为多面体组成面且高度为内切球半径的多面体，则：

$V_o={\displaystyle {\sum }_{i=0}^n{K}^2{S}_i\ast \left(1-K\right)R}=3\left(K^2-K^3\right)V_s$ (5)

其中， $V_o$ 为开孔体积， $S_i$ 为组成胞元的面对应的表面积， $R$ 为胞元内切球半径。

则各胞元孔隙率 $\text{Φ}$ 与缩放系数 $K$ 之间的函数对应关系为：

$\varphi =\frac{V_c+V_o}{V_s}=3K^2-2K^3$ (6)

由此可见，在模型生成的过程中，孔隙率仅与缩放系数密切相关，与随机点数量等设计参数不存在直接关系。

3.2. 孔径

孔径是材料内部微孔通道的截面尺寸，其大小直接关乎渗透、过滤及导热等性能。对于多孔植入物而言，孔径的取值会影响氧气和营养物质的运输，对骨细胞的增殖和黏附具有重要影响意义。

对于不规则多孔而言，孔道的数量极多且形状各异，无法利用统一标准进行评估。鉴于此，本文将孔道的不规则多边形等效为面积相等的圆，采用各胞元的孔径均值来表征多孔结构整体的孔径水平。

$D_{pore}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\sqrt{\frac{4S_i}{\text{π}}}}$ (7)

式中， $D_{pore}$ 为等效孔径， $S_i$ 为泰森多面体胞元外表面的面积。

构建20 mm × 20 mm × 60 mm的设计空间，设置变量为随机点数量和缩放系数，其中随机点数量变化区间为50~500个，缩放系数变化区间为0.500~0.804，对应孔隙率区间范围为50%~90%。根据不同的输入条件，进行等效孔径的测算，后续孔棱直径以及比表面积的测算方式与此一致，不再赘述。最终得到孔径与设计参数间的关系如图5所示。

Figure 5. Aperture regulation diagram

图5. 孔径调控图

从整体趋势来分析，孔径受随机点数量和缩放系数的共同作用影响，其中受随机点数量影响较为显著，且当点的数量增加至一定规模时，孔径会出现拐点并趋近于一个稳定值。以缩放系数为0.500为例，起初随机点数量较少即点密度较低时，孔径随着点的增加而快速减小，当随机点数量增加至一定规模时出现拐点，随着随机点的持续密布，孔径减小的速度大幅下降。以随机点数量为500个为例，可以直观的看到缩放系数与孔径呈线性关系，且孔径随缩放系数的增加而增加。

3.3. 孔棱直径

孔棱是多孔材料中固相的主要存在形式，也是开孔结构中孔道的外轮廓及支撑结构，其长度、截面形状和尺寸以及相互之间连接时形成的角度等参数是在一定程度上直接决定了材料的力学性能。

与孔径的表征方法类似，将孔棱的截面等效为面积相等的圆，采用各孔棱直径的均值来表征多孔结构整体的孔棱直径水平。

$D_{arris}=\frac{1}{m}{\displaystyle \underset{j=1}{\overset{m}{\sum }}\sqrt{\frac{4S_j}{\text{π}}}}$ (8)

式中， $D_{arris}$ 为等效孔棱直径， $S_j$ 为孔棱截面的面积。

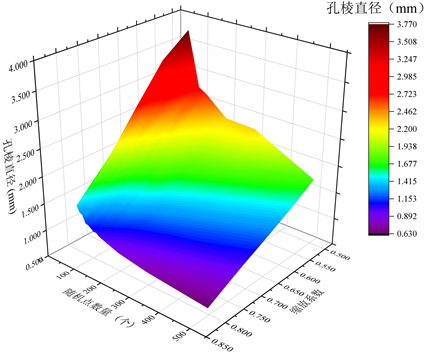
Figure 6. Prism diameter regulation diagram

图6. 孔棱直径调控图

如图6所示，孔棱直径同样受设计参数的共同作用影响，当随机点数量增至一定规模时，孔棱直径将趋于稳定。以缩放系数为0.500为例，起初随机点较少时，孔棱的尺寸随着点的增加而快速减小。当随机点数量经过拐点后，随着随机点的持续密布，降幅逐渐变缓。以随机点数量为500为例，孔棱直径随缩放系数的增加而减小，整体显现严格的线性关系。

3.4. 比表面积

在通用骨分析参数中，骨表面积骨体积比被用于表征单位体积骨组织的面积大小，参照其定义方式，选取面积体积比进行比表面积计算。一般而言，比表面积越大的多孔材料，吸附能力越强。对于多孔植入物而言，较大的比表面积能为骨细胞的黏附和增殖提供有利条件，便于其进行营养物质的吸附和降解产物的排放，从而更好地实现骨整合。

如图7所示，比表面积与缩放系数、随机点数量相互关联，当缩放系数和随机点数量分别增加时，比表面积均会随之增长。以缩放系数为0.500为例，一开始随机点数量较少时，比表面积的增长速率较高，随着随机点的持续密布，比表面积的增长会逐渐放缓。以随机点数量为500为例，比表面积与缩放系数呈现近似幂函数的关系，且增速随着缩放系数的增长而不断提升。

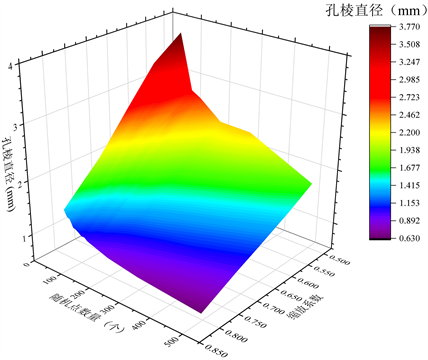
Figure 7. Specific surface area regulation diagram

图7. 比表面积调控图

4. 讨论

对于均质多孔模型而言，不同的生成方式决定了调控孔隙率的设计参数必然存在区别。自2010年Kou提出将泰森多边形原理应用于多孔材料的设计以来，不规则多孔模型主要存在两种主流的设计方法。其一是Wejrzanowski、Xiao等在完成泰森分割后，提取多面体轮廓线，以线框结构为基础进行杆件生成，通过控制杆件半径实现孔隙率调控，研究发现孔隙率随着杆件半径的增加而减小，呈现近似线性的关系。其二是Gómez、Fantini等在生成泰森多面体后，对其胞元进行体缩放和面缩放处理，以特定顶点构建四面体网格，并利用Catmull-Clark算法对得到的网格结构进行细分圆滑处理，通过控制体缩放系数和面缩放系数进行孔隙率调整，研究发现当两个系数一致时，孔隙率随缩放系数的增加而增加，呈现近似线性的关系。如图8所示，与前人的设计方法相比，本文提出的设计方法确定了孔隙率与设计参数之间的唯一确定函数关系，实现了精准控制，与此同时也拓展了孔隙率的研究范围。

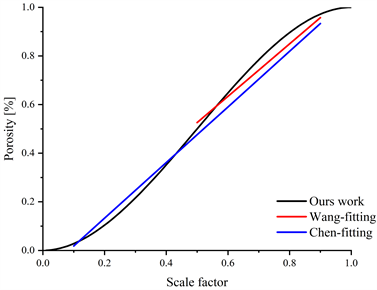
Figure 8. Scaling factor-porosity relationship

图8. 缩放系数–孔隙率关系图

在几何参数与设计参数宏观关系研究的基础上，开展设计参数对模型内部微观结构的控制讨论以及结构变动对几何参数的作用机制探究。

当设计空间确定不变时，增加随机点数量意味着泰森胞元的增加，此时新增点必然落入某个胞元内或出现在多面体的某个面上，因此可以将其理解为在一个有限的空间中再次进行了泰森分割，这势必会导致胞元的尺寸有所缩减，从而造成孔径的减小。当孔隙率不发生改变时，有限空间的重新划分也代表着有限固相体积的重新分配，固相支架随胞元数量的增加而变得复杂，与之相匹配的，孔棱直径会逐渐减小，比表面积逐渐增加。

点密度较低时，胞元数量较少，即微孔通道和孔棱数量较少，因此等效孔径、孔棱直径较大而比表面积却相对较小，此时增加随机点数量进行空间分割，对三者的影响幅度较大。但随着点的逐渐密布，用于新增点分割的区域会逐渐被压缩，对原有结构的改变也会逐渐降低，此时微孔通道和孔棱都已形成一定的规模，参数调控带来的变化在全局中的权重下降，模型几何参数的变化幅度也就随之下降而趋于稳定。

当空间点密度确定时，基于泰森多边形原理可知多孔模型的结构也是唯一确定的。从单个胞元的构建出发进行分析，缩放系数带来的影响发生在镂空和开孔环节，由于对体缩放和面缩放采用了相同的系数进行控制，因此缩放后的多面体各面面积即表示微孔通道尺寸，这很好地解释了孔径与缩放系数间呈现的严格线性关系，且其对应关系的曲线斜率可视为通孔多边形转化为等效圆时的综合等效系数。

更进一步地，开孔处理完后剩余的固相材料构成了孔棱，因此孔棱直径与缩放系数间的关系也是严格的线性关系，且其斜率可视作孔棱多边形转化为等效圆时的综合等效系数。

在多孔骨架结构不变的前提下，缩放系数增长会孔棱直径减小。此时孔棱的长度不变，但横截面会逐步缩减，结合比表面积的定义，不难理解比表面积的增速会随缩放系数的增长而加快。

基于对设计参数和几何参数内在关系的理解，在进行不规则多孔设计的时候，可以参考以下建模思路：在孔隙率设计目标的允许范围内，给定一个初始缩放系数，优先确定一个合理的点密度值，将孔径、孔棱直径的变化范围及幅度缩小，然后根据具体的设计需求，进一步调整随机点数量和缩放系数。采取区间粗略定位和数值精细调控两步走的方法可以快速实现模型的结构调控，进而满足不同的应用场景和个性化需求。

5. 总结

本文提出了一种基于泰森多边形的仿生多孔结构设计方法，可应用于骨科植入物的参数化构建，以期通过模拟自然骨结构加强骨再生能力。通过深入开展设计参数与多孔模型几何参数间之内在关联的探究，包括孔隙率、等效孔径、孔棱直径、比表面积，提出了个性化定制和微观结构调控方案。与其他方法相比，本文提出的设计方法优势在于引入了仿生的随机性但又提供了几何的可控性。该方法提供了一种直观且便捷的工作流来创建仿生多孔结构，并可进一步扩展至其他组织工程或其他多孔结构领域。