电磁场作用下奇粘性对薄膜稳定性影响的数值模拟

Numerical Simulation of the Effect of Odd Viscosity on Film Stability in Presence of Electromagnetic Field

摘要: 本文研究了在电磁场存在的情况下，时间反转对称性被打破时，奇粘性对沿倾斜平面流动的液体薄膜稳定性的影响。采用线方法数值模拟了Zhao和Jian得出的非线性气液界面演化方程。得到了固定时间下，薄膜厚度随奇粘性的变化情况。验证了奇粘性对薄膜不稳定性的抑制作用，并且分析了哈特曼数对奇粘性抑制作用的影响。通过数值模拟得到在不同奇数粘性下，薄膜随着时间和空间演化的图像。图像清晰的显示了不同奇数粘性下薄膜界面演化情况。所得结果能够更好地证明奇粘性的稳定性作用，与之前的研究结论相统一。

Abstract: In the presence of an electromagnetic field, the influence of odd viscosity on the stability of a liquid film flowing along an inclined plane when the time reversal symmetry is broken is analyzed. The nonlinear gas-liquid interface evolution equation obtained by Zhao and Jian was numerically simu-lated using line method. The variation of film thickness with odd viscosity at fixed time is obtained. The inhibition effect of odd-viscosity on film instability is verified and the influence of Hartmann number on odd-viscosity inhibition is analyzed. The time and space evolution images of thin film with different odd viscosity are obtained by numerical simulation. The image clearly shows the film interface evolution under different odd viscosity. The results can better prove the stability effect of odd viscosity, which is consistent with the conclusion of previous study.

1. 引言

薄膜在物理、化学和生物工业中得到广泛应用，其界面稳定性分析一直是流体力学中一个热门研究课题。薄膜技术在硬涂层和耐腐蚀涂层、激光切割工艺、生物技术和医学等多个领域中具有重要意义。例如，在激光切割过程中，不希望产生表面波。在涂层膜的表面产生的不稳定性会降低产品的质量。因此，对这种不稳定性的控制具有极大的实际意义。此外，随着导电液体薄膜被广泛应用到核能设备以及冶金技术等工业领域中，越来越多的学者开始研究电磁场存在时液体薄膜流动的稳定性。Dholey [1] 研究了均匀电磁场对沿斜面流动的导电粘弹性液体薄膜稳定性的影响，发现磁性参数具有稳定作用，粘弹性参数和电参数都具有不稳定作用。Tsai [2] 等人分析了在均匀磁场影响下，沿垂直平板流动的导电液体冷凝膜的非线性稳定性，发现磁场能够稳定薄膜流动。Mukhopadyay [3]，Korsunsky [4] 等人研究了在电磁场存在下沿斜面流动的粘性导电薄膜的稳定性。利用长波近似方法导出了液体自由面的非线性演化方程。演化方程的稳定性分析表明，磁场对流动起稳定的作用，而电场对流动是否具有稳定作用主要取决于电场的方向，即当电场为正时，它对流动有不稳定作用，当电场为负时，其有助于稳定流动。

众所周知，粘度是流体的一个基本性质，通常把它与耗散联系起来。在以往的稳定性分析中，为了理解和预测各个物理参数对系统的影响，在流体控制方程中总是应用标准应力张量。直到Avron [5] [6] 在量子霍尔效应的研究中开创性地发现，对于经典流体，由于自发地、外部磁场或旋转导致时间反转对称性被打破，粘度张量还存在一个无耗散的奇数部分，称为霍尔粘度或奇粘度。近几年，关于奇粘性对薄膜稳定性影响的研究不断有新进展。Bao和Jian [7] 研究了在外加电场作用下，奇粘性对液体薄膜不稳定性的影响，发现奇粘性具有稳定效应，而电场具有不稳定的作用。Chattopadhyay [8] 探索了在均匀法向电场作用下，非均匀加热斜面上具有奇粘性的流体薄膜的稳定性和动力学。研究表明，奇粘性对流动有稳定作用，而电场使得流动有不稳定倾向。

Zhao和Jian [9] 分析了电磁场作用下奇粘性对流体薄膜稳定性的影响，利用长波近似理论推导出含有奇粘性效应的气液界面演化方程，通过线性分析，发现奇粘性和磁场对流动有稳定影响，而电场则使流动变得不稳定。本文旨在对上述研究用数值计算对非线性演化方程进行模拟，采用线方法研究奇粘性在电磁场作用下对流体薄膜稳定性的影响。

2. 数学模型

模型示意图及图中参数说明参照Zhao和Jian [9] 中的图1。在打破时间反演对称性的液体中，柯西应力张量S由两部分组成：S = S^e + S^o，其中S^e和S^o分别是柯西应力张量的偶数部分和奇数部分。二维的液膜流动可以表示为 [10] ：

$S_{ij}^e=-p{\delta }_{ij}+{\mu }^e\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$ (1)

$S_{ij}^o=-{\mu }^o\left({\delta }_{i1}{\delta }_{j1}-{\delta }_{i2}{\delta }_{j2}\right)\left(\frac{\partial u_1}{\partial y}+\frac{\partial u_2}{\partial x}\right)+{\mu }^o\left({\delta }_{i1}{\delta }_{j2}+{\delta }_{i2}{\delta }_{j1}\right)\left(\frac{\partial u_1}{\partial x}-\frac{\partial u_2}{\partial y}\right)$ (2)

其中下标i，j = 1，2，μ^e和μ^o分别为偶数和奇数粘度系数。Navier-Stokes方程可以表示为：

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$ (3)

$\rho \left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)=-\frac{\partial p}{\partial x}+{\mu }^e\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)+\sigma B_0\left(E_0-u{B}_0\right)+\rho g\sin \theta -{\mu }^o\left(v_{xx}+v_{yy}\right)$ (4)

$\rho \left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)=-\frac{\partial p}{\partial y}+{\mu }^e\left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}\right)-\rho g\cos \theta +{\mu }^o\left(u_{xx}+u_{yy}\right)$ (5)

其中u和v分别是x方向和y方向的速度场，r为流体密度，p表示压强，s是流体的电导率，B₀是磁场强度，E₀代表电场强度。

在固-液界面y = 0处施加无滑移、无渗透边界条件

$u=v=0$ (6)

自由面 $y=h\left(x,t\right)$ 处的运动学边界条件为

$v=h_t+u{h}_x$ (7)

考虑在 $y=h\left(x,t\right)$ 处切向应力和法向应力平衡得到边界条件

$h_x\left(v_y-u_x\right)+\left(1-h_x^2\right)\left(u_y+v_x\right)+\frac{{\mu }^o}{{\mu }^e}\left[\left(1-h_x^2\right)\left(u_x-v_y\right)+2h_x\left(u_y+v_x\right)\right]=0$ (8)

$-p+\frac{{\mu }^e}{1+h_x^2}\left\{-2h_x\left(v_x+u_y\right)+2h_x^2{u}_x+2v_y+\frac{{\mu }^o}{{\mu }^e}\left[\left(1-h_x^2\right)\left(u_y+v_x\right)-2h_x\left(u_x-v_y\right)\right]\right\}=\frac{h_{xx}{\sigma }_0}{{\left(1+h_x^2\right)}^{3/2}}$ (9)

采用润滑理论，假设薄膜界面形变的波长λ要远远大于薄膜的平均厚度h₀，即 $\lambda \gg h_0$ 。定义薄膜参数 $\epsilon =h_0/\lambda \ll \text{1}$ [11] [12] [13]，并定义以下无量纲参数：

$x^{\ast }=\frac{x}{\lambda }$ , $\left(h^{\ast },y^{\ast }\right)=\frac{\left(h,y\right)}{h_0}$ , $t^{\ast }=\frac{t}{\lambda /U_0}$ , $u^{\ast }=\frac{u}{U_0}$ , $v^{\ast }=\frac{u}{\epsilon U_0}$ , $p^{\ast }=\frac{p}{\rho U_0^2}$ (10)

其中 $U_0=\rho g{h}_0^2\sin \theta /\left(3{\mu }^e\right)$ 为Nusselt速度。在之后的表达式中去掉星号，将无量纲变量代入控制方程和边界条件得到的方程参见Zhao和Jian [9]。其他无量纲参数雷诺数Re、弗劳德数Fr、韦伯数We、哈特曼数M、电参数E的形式分别为

$Re=\frac{U_0{h}_0\rho }{{\mu }^e}$ , $Fr=\frac{U_0^2}{g{h}_0}$ , $We=\frac{{\sigma }_0}{\rho U_0^2{h}_0}$ , $M=B_0{h}_0\sqrt{\sigma /{\mu }^e}$ , $E=\frac{E_0}{B_0{U}_0}$ (11)

并且在简化中利用了由Nusselt速度定义的sinθ/Fr = 3/Re关系。通过下列关于小参数ε的正则摄动展开：

$u=u_0+\epsilon u_1+o\left({\epsilon }^2\right)$ , $v=v_0+\epsilon v_1+o\left({\epsilon }^2\right)$ , $p=p_0+\epsilon p_1+o\left({\epsilon }^2\right)$ (12)

忽略Ο(ε)项和更高阶项，直接将展开后的变量代入模型的无量纲方程，推导出主导阶方程并求解，得

$u_0=\frac{w}{M^2}\left[1-\frac{\cosh M\left(h-y\right)}{\cosh \left(Mh\right)}\right]$ , $w=3+E{M}^2$ (13)

$v_0=\frac{w\mathrm{sech}{\left(Mh\right)}^2{h}_x}{M^2}\left[1-\cosh \left(My\right)\right]$ (14)

$p_0=\frac{\cos \theta }{FrRe}\left(h-y\right)-\frac{{\mu }^o}{{\mu }^{e}Re}\frac{w\mathrm{sech}\left(Mh\right)\sinh \left(h-y\right)}{M}-{\epsilon }^{2}We{h}_{xx}$ (15)

同理得到一阶方程并求解得到一阶解

$\begin{array}{c}{u}_1=R\left[1-\frac{\cosh M\left(h-y\right)}{\cosh \left(Mh\right)}-\frac{M}{2}\left(h-y{\cosh }^2\left(Mh\right)\right)\frac{\sinh \left(My\right)}{{\cosh }^2\left(Mh\right)}-\frac{M}{2}y\tanh \left(Mh\right)\cosh \left(My\right)\right]h_x\\ -\frac{3\cot \theta }{M^2}\left[1-\frac{\cosh M\left(h-y\right)}{\cosh \left(Mh\right)}\right]h_x-\frac{2{\mu }^{o}w\tanh \left(Mh\right)}{{\mu }^e{M}^2{\cosh }^2\left(Mh\right)}\sinh \left(My\right)h_x+\frac{{\epsilon }^{2}ReWe}{M^2}\left[1-\frac{\cosh M\left(h-y\right)}{\cosh \left(Mh\right)}\right]h_{xxx}\end{array}$ (16)

这里 $R=w^{2}Re\tanh \left(Mh\right)/\left(M^5{\cosh }^2\left(Mh\right)\right)$ 。u₁中包含了奇粘性效应，这是由于奇粘性导致系统中产生了额外的应力。此外，通过如下关系式定义流向流量

$q\left(x,t\right)={\displaystyle {\int }_0^{h\left(x,t\right)}u\left(x,y,t\right)\text{d}y}$ (17)

其中 $u\left(x,y,t\right)=u_0\left(x,y,t\right)+\epsilon u_1\left(x,y,t\right)$ 。运动学边界条件可以替换为如下形式

$h_t+q_x=0$ (18)

将式(17)代入式(18)后得到薄膜界面演化方程

$h_t+D\left(h\right)h_x+\epsilon {\left[E\left(h\right)h_x+{\epsilon }^{2}F\left(h\right)h_{xxx}\right]}_x=0$ (19)

再做变换 $\epsilon \left({\partial }_t,{\partial }_X\right)\to \left({\partial }_t,{\partial }_X\right)$ ，方程(19)可以转化为：

$h_t+D\left(h\right)h_x+{\left[E\left(h\right)h_x+F\left(h\right)h_{xxx}\right]}_x=0$ (20)

其中

$D\left(h\right)=w{\left(\frac{\tanh \left(Mh\right)}{M}\right)}^2$ (21)

$\begin{array}{c}E\left(h\right)=\frac{3}{2}R\left(h-\frac{\tanh \left(Mh\right)}{M}-\frac{h{\tanh }^2\left(Mh\right)}{3}\right)-\frac{3\cot \theta }{M^2}\left(h-\frac{\tanh \left(Mh\right)}{M}\right)\\ -\frac{2{\mu }^{o}w}{{\mu }^e{M}^2{\cosh }^2\left(Mh\right)}\left(\frac{\sinh \left(Mh\right)}{M}-\frac{\tanh \left(Mh\right)}{M}\right),\end{array}$ (22)

$F\left(h\right)=\frac{ReWe}{M^2}\left(h-\frac{\tanh \left(Mh\right)}{M}\right)$ (23)

式(19)是Zhao和Jian [9] 推导的结果。可以从系数E(h)中看出，非零的奇粘性μ^o会对薄膜的演化方程产生新的影响.式(19)与文献 [14] 中的式(2.22)之间唯一的差异是E(h)包含了奇粘性项。下面我们将对方程(20)进行数值模拟。

3. 数值模拟

本文采用线方法 [15] 来模拟薄膜的时空演化。演化方程(20)改写为

$h_t+q_x=0$ (24a)

其中

$q=w\left(\frac{Mh-\tanh \left(Mh\right)}{M^3}\right)+E\left(h\right)h_x+F\left(h\right)h_{xxx}$ (24b)

由于方程(24a)是一个四阶偏微分方程，故需要四个边界条件和一个初始条件。边界条件可以表示为：

$h\left(L,t\right)=0.1$ , $h_x\left(L,t\right)=0$ , $h_x\left(0,t\right)=0$ , $h_{xxx}\left(0,t\right)=0$ (25)

其中L为域的无量纲长度。初始条件表示为：

$h\left(x,0\right)=1+0.05\cos \left(kx\right)$ (26)

构造一个空间网格 $x_i=\left(i-1\right)\Delta x,i=1,2,\cdots ,N$ 离散非线性演化方程，其中Δx = L/N。网格点处的薄膜厚度值用h_i表示，h_i仅为时间函数，满足N个一阶常微分方程

$h_{it}+\frac{q_{i+\frac{1}{2}}-q_{i-\frac{1}{2}}}{\Delta x}=0$ (27a)

当i在3和N − 2之间时，

$\begin{array}{c}{q}_{i+\frac{1}{2}}=w\left(\frac{M\frac{h_{i+1}+h_i}{2}-\tanh \left(M\frac{h_{i+1}+h_i}{2}\right)}{M^3}\right)+(-\frac{3\cot \theta }{M^2}\left(\frac{h_{i+1}+h_i}{2}-\frac{\tanh \left(M\frac{h_{i+1}+h_i}{2}\right)}{M}\right)\\ +\frac{3}{2}R\left(\frac{h_{i+1}+h_i}{2}-\frac{\tanh \left(M\frac{h_{i+1}+h_i}{2}\right)}{M}-\frac{\frac{h_{i+1}+h_i}{2}{\tanh }^2\left(M\frac{h_{i+1}+h_i}{2}\right)}{3}\right)\\ -\frac{2{\mu }^{o}w}{{\mu }^e{M}^2{\cosh }^2\left(M\frac{h_{i+1}+h_i}{2}\right)}\left(\frac{\sinh \left(M\frac{h_{i+1}+h_i}{2}\right)}{M}-\frac{\tanh \left(M\frac{h_{i+1}+h_i}{2}\right)}{M}\right))\frac{h_{i+1}-h_i}{\Delta x}\\ +\frac{ReWe}{M^2}\left(\frac{h_{i+1}+h_i}{2}-\frac{\tanh \left(M\frac{h_{i+1}+h_i}{2}\right)}{M}\right)\frac{h_{i+2}-3h_{i+1}+3h_i-h_{i-1}}{\Delta x^3},\end{array}$ (27b)

$\begin{array}{c}{q}_{i-\frac{1}{2}}=w\left(\frac{M\frac{h_i+h_{i-1}}{2}-\tanh \left(M\frac{h_i+h_{i-1}}{2}\right)}{M^3}\right)+(-\frac{3\cot \theta }{M^2}\left(\frac{h_i+h_{i-1}}{2}-\frac{\tanh \left(M\frac{h_i+h_{i-1}}{2}\right)}{M}\right)\\ +\frac{3}{2}R\left(\frac{h_i+h_{i-1}}{2}-\frac{\tanh \left(M\frac{h_i+h_{i-1}}{2}\right)}{M}-\frac{\frac{h_i+h_{i-1}}{2}{\tanh }^2\left(M\frac{h_i+h_{i-1}}{2}\right)}{3}\right)\\ -\frac{2{\mu }^{o}w}{{\mu }^e{M}^2{\cosh }^2\left(M\frac{h_i+h_{i-1}}{2}\right)}\left(\frac{\sinh \left(M\frac{h_i+h_{i-1}}{2}\right)}{M}-\frac{\tanh \left(M\frac{h_i+h_{i-1}}{2}\right)}{M}\right))\frac{h_i-h_{i-1}}{\Delta x}\\ +\frac{ReWe}{M^2}\left(\frac{h_i+h_{i-1}}{2}-\frac{\tanh \left(M\frac{h_i+h_{i-1}}{2}\right)}{M}\right)\frac{h_{i+1}-3h_i+3h_{i-1}-h_{i-2}}{\Delta x^3},\end{array}$ (27c)

由于i = N + 1对应x = L，根据边界条件(24)，该端点处薄膜厚度值为0.1，故h_N+1 = 0.1。用域外的点(鬼点)来表示边界附近的导数，得到h_N+2 = h_N。在x = L，利用对称性条件得到h₀ = h₂，h₋₁ = h₃，从而可以用Matlab中标准微分方程求解器求解。

为便于讨论电磁场作用下奇粘性对薄膜演化过程的影响，参考文献 [9] 给出的物理参数范围：奇粘性与偶粘性之比m (μ^o/μ^e)为0~1.5，哈特曼数M为0~2。此外，在下文所有分析中考虑We = 430，Re = 0.5，E = 0.5。

图1显示了无量纲时间t = 80时，薄膜厚度随奇数粘度变化的图像。其中从图1(a)中可以发现，随着奇粘性比值的增加薄膜振幅变得更低。这证明奇粘性对薄膜的不稳定性具有抑制作用，这与之前Zhao和Jian [9] 的研究结论相同。从数值模拟上进一步验证了之前的结论。比较图1(a)~(d)可以得到，当雷诺数较小时，随哈特曼数M的增加，薄膜振幅下降，这说明磁场会抑制薄膜流动的不稳定性。

图2显示了在奇粘性取不同值时，薄膜厚度随时间演化的图像。其中无量纲的时间取值为t = 1~30。从图中可以观察到，随着时间的增加薄膜厚度不断增加，表明随着时间薄膜变得越发不稳定。比较图2(a)~(d)得到，奇粘性的增加使得薄膜厚度变的更低，随着时间演化振幅增加的速度也变的更慢。这进一步验证了奇粘性对薄膜不稳定性的抑制作用。

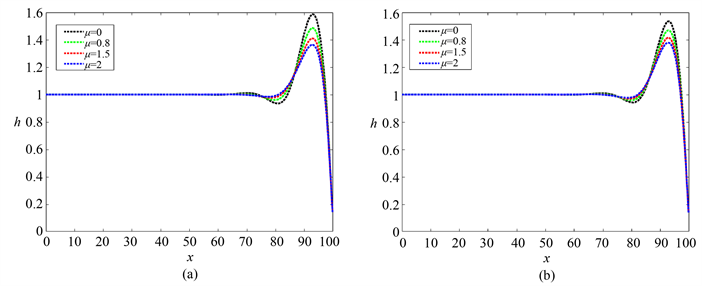
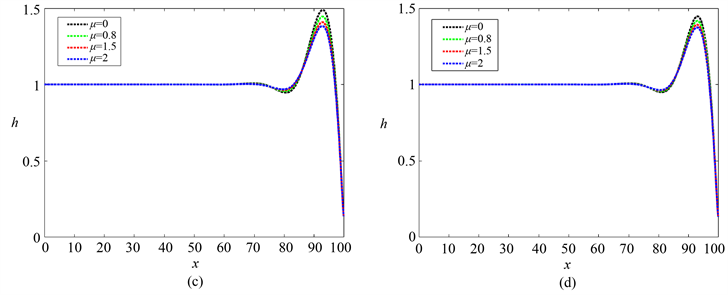
Figure 1. Images of film thickness varying with odd viscosity when the dimensionless time t = 80 with different values of Hartmann number. μ = 0, 0.8, 1.5, 2. (a) M = 0.5, (b) M = 1, (c) M = 1.5, (d) M = 2

图1. 在无量纲时间t = 80，哈特曼数取不同值时，薄膜厚度随奇粘性变化的图像。μ = 0，0.8，1.5，2。(a) M = 0.5，(b) M = 1，(c) M = 1.5，(d) M = 2

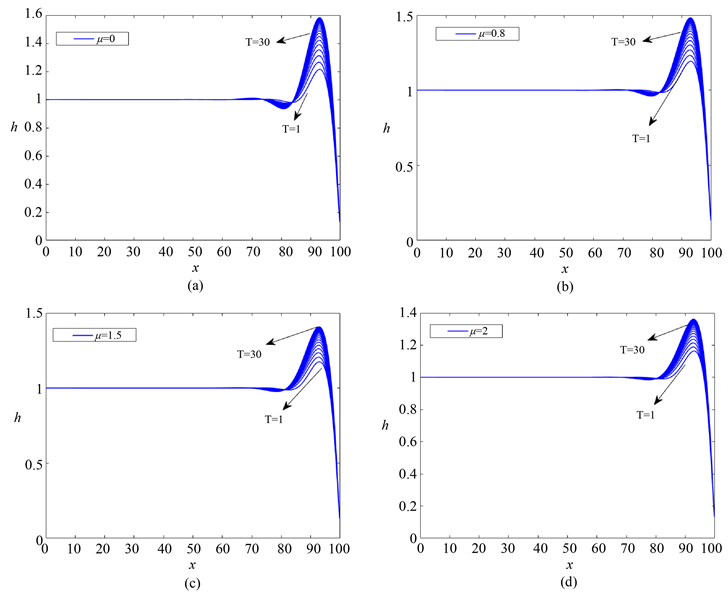
Figure 2. Images of film thickness evolution over time t = 1~30 at M = 0.5 with different odd viscosity: (a) μ = 0, (b) μ = 0.8, (c) μ = 1.5, (d) μ = 2

图2. M = 0.5时不同奇数粘度下，薄膜厚度随时间t = 1~30演化的图像：(a) μ = 0，(b) μ = 0.8，(c) μ = 1.5，(d) μ = 2

图3展示了在奇粘性取不同值时，薄膜厚度随时间和空间演化的三维图像。图中的颜色高亮部分表示更高的薄膜厚度，从图中右侧的标注我们可以得到，随着奇粘性的增加，薄膜振幅变得更低。这也更加验证了奇粘性对薄膜不稳定的抑制作用。

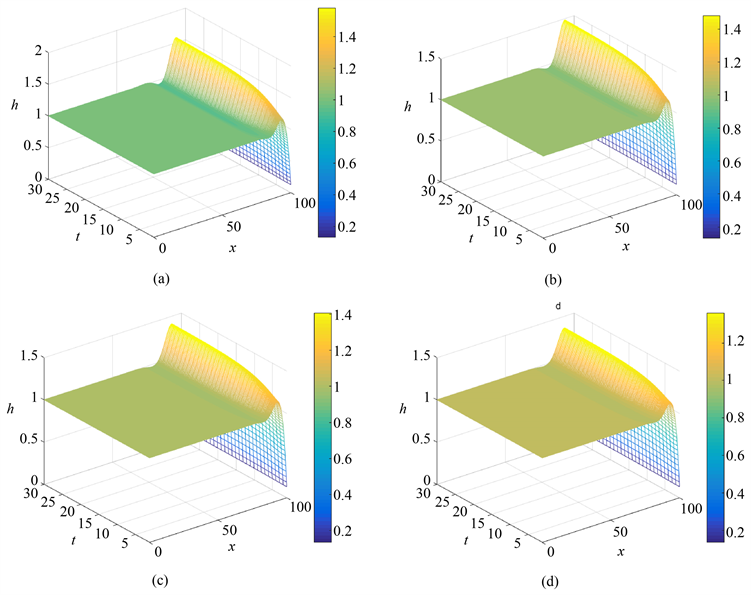
Figure 3. Three-dimensional images of film thickness evolution with time and space at M = 0.5 with different odd viscosity: (a) μ = 0, (b) μ = 0.8, (c) μ = 1.5, (d) μ = 2

图3. 不同奇粘性下，薄膜厚度随时间和空间演化的三维图像：(a) μ = 0，(b) μ = 0.8，(c) μ = 1.5，(d) μ = 2

4. 结论

以往关于薄膜稳定性的研究大多集中于具有标准粘性(偶粘性)的液体，直到Avron [5] [6] 在量子霍尔效应的实验中发现磁场等因素会导致流体的时间反演对称性被打破，从而产生第二个粘性系数，即奇粘性系数。本文研究了在电磁场存在的情况下，奇粘性对沿斜面流动的液体薄膜稳定性的影响。Zhao和Jian [9] 已经推导出气液界面非线性演化方程，并进行了线性和弱非线性稳定性分析，但未通过数值模拟去加强结论。因此本文采用线方法对非线性演化方程求解，通过数值模拟清晰的展示了自由表面演化过程随粘性比μ和哈特曼数M的变化情况。发现随着奇粘性比值的增加薄膜振幅变得更低，且当雷诺数较小时，薄膜振幅随哈特曼数M的增加而下降。从而成功地证实了奇粘性和磁场对液体薄膜流动具有稳定作用。在本研究的基础上，日后可以考虑薄膜界面有活性剂或外部施加周期振动时奇粘性对其稳定性的影响并进行数值模拟。

基金项目

本研究由国家自然科学基金地区项目(12262026)、内蒙古自然基金面上项目(2021MS01007)、内蒙古自治区党委组织部：2019年“草原英才”滚动支持项目(12000-12102408)和内蒙古自治区高等学校创新团队发展计划支持(NMGIRT2323)资助。

NOTES

^*通讯作者Email: [e-mail]