中国保险业规模的变动分析——基于时间序列模型的选择与优化

The Change Analysis of China’s Insurance Industry Scale—Based on ARIMA Model

摘要: 文章基于时间序列模型对我国保险业规模的变动进行了分析预测。在分析理论机制的基础上，主要选取从广度的角度体现保险规模的保险密度指标，通过对我国改革开放后1980~2019年的保险密度时间序列数据的分析，找出的最优模型是ARIMA (1, 1, (1, 4))模型，并进行了为期5年的预测，之后对比2020年、2021年度真实的保险密度值，发现该模型对短期中国保险密度年度数值有较好的预测效果。

Abstract: Based on the time series model, this paper analyzes and predicts the changes of the scale of our in-surance industry. Based on the analysis of the theoretical mechanism, the insurance density index which reflects the insurance scale from the perspective of breadth is selected. Through the analysis of the insurance density time series data from 1980 to 2019 after China’s reform and opening up, the optimal model is found to be ARIMA (1, 1, (1, 4)) model, and the five-year forecast is carried out. After comparing the real insurance density values in 2020 and 2021, it is found that the model has a good prediction effect on the short-term annual value of China’s insurance density.

1. 引言

改革开放以来，保险业在我国愈发盘踞了一席地位，保险业的发展在一定程度上支撑着我国经济发展的稳定性，我国各界对保险业的规模以及发展也愈发的重视。2014年《国务院关于加快发展现代保险服务业的若干意见》中明确指出：到2020年，我国保险业的深度要达5%，保险密度要向3500元/人的目标看齐 [1]。由此可见，我国对保险业的规模发展已经不再拘泥于基础性指标，而是拓展到对保险业覆盖的高广度以及高深度的目标中。据《中国保险年鉴2018》的基础统计信息知，我国保险行业2007年实现全年保费收入36581.01亿元，在数量上已成为全球第二大保险市场经济体 [2] ；从时间段变化数据来看，1997年我国的保费收入为1087亿元，经过数十年的发展，到2019年我国保费收入飞升为4.27亿元，年均增长速度达到了18%。以上统计数据表明我国保险业的发展取得了斐然的成绩，保险业的规模在一定程度上也取得了巨大的成就。

在“十四五”时期新的发展形势下，我国保险业的规模及发展将迎来更大的挑战和机遇，很多学者预测我国保险规模将进一步扩大、保费收入也将进一步增多，对我国保险业规模及发展水平的科学预测不仅有利于国家精准的完成“十四五”时期制定的保险指数目标，提高我国保险资源配置的效率，还能在一定程度上提高百姓对保险的重视程度，为百姓的生活争取到更大的保障 [3] [4]。对保险规模发展水平的预测主要分为对保费收入的预测、对保险密度的预测以及对保险深度的预测，其中对保费收入的预测是衡量保险业规模发展水平的基础性指标，对保险密度以及保险深度的预测相对来说更为深入。因此，本文将基于时间序列的ARIMA模型从广度的角度对体现我国保险规模的保险密度指标进行预测。

2. 文献综述

保险业是我国金融行业的重要组成部分，随着我国政府对保险业支持力度的不断加大，该行业在我国国民经济发展过程中发挥的作用愈发不可替代，对保险业规模的分析和预测也愈发重要。当前各界通常使用保费收入、保险深度(保费收入占GDP的比重)、保险密度(人均保费收入)等指标来衡量某地区保险业的规模发展水平的数字特征情况。其中，保费收入是用来体现保险业规模的基础性指标，保险深度和保险密度通常用来描述保险业规模发展的广度及深度，是保险业发展规模的高阶指标 [5] [6]，前者反映了该地区的保险普及率，后者则体现了保险业在该地区经济发展过程中的地位。本节将近年来对于我国保险业规模变动的研究进行梳理，主要从我国保险业规模预测研究等方面进行文献的回顾和评述。

保险业规模的预测作为我国保险领域的重要问题之一，已有部分学者采用各种定量分析方法对其进行了预测，其中，回归模型、灰色系统理论、时间序列模型等方法在保险业发展规模的预测中应用的最为广泛。另外，近些年来也有学者将上述方法结合在一起，使用组合预测的形势对保险问题进行定量预测。

基于回归模型对保险业规模预测是最为传统的一种方法，一般需要对影响保险规模的因素进行定量估计，然后将其带入到回归方程中，从而根据关系式可以对保险规模进行合理的预测，该方法最大的优点在于预测时可以考虑到各影响因素的影响程度。粟芳(2000)利用我国保险相关数据构造了人均GDP和保险密度的长短期模型，结果表明线性回归分析方法更适用于保险业规模的短期预测 [7]。吴开兵等(2000)结合我国经济发展的趋势，基于Logistic模型对我国保险业规模的保险深度指标进行了定量预测 [8]。黄佐钘等(2003)基于我国保险业发展现状，利用多元回归分析方法对我国年度保费收入以及分险种保费收入进行了预测 [9]。尹远成等(2008)利用回归模型将影响我国人身保险保费收入的存款余额等五个因素的作用分解出来，然后对未来五年我国人身保险保费收入进行了预测 [10]。需要指出的是，利用回归模型对保险业规模进行预测的做法在近几年减少了许多。

我国学者还使用了灰色预测模型对保险规模进行了预测。赵长利等(2007)、时乐乐等(2012)基于灰色预测模型的原理对我国保费收入进行了专门的分析，进而对保险业未来发展趋势做出了科学的定量预测 [11] [12]。张积林(2010)以我国1980年以来28年的全国保险业保费收入为基础，采用完全的灰色理论对我国未来7年的保费收入进行了定量的预测，并在定量分析的基础上对我国未来保险业规模的发展进行定性分析 [13]。张鑫等(2018)创新性地构建灰色最优预测模型DRGM(1,1)对东北三省地区的保费收入进行了合理地预测，此种改进提高了模型预测的精度 [14]。灰色预测模型最大的优点是不需要大样本空间数据就可以进行较为精确的预测，但在具体操作过程中可能会出现过度拟合等问题 [15]。

采集历史数据进行时间序列分析的预测方法在国内也较为常见。梁来存等(2006)基于数据特征建立了时间序列的ARIMA模型，进而对我国保费收入月度数据进行了短期定量预测 [16]。付宇涵(2010)利用求和自回归移动平均模型对我国保险业财产险收入的变化趋势进行了定量预测 [17]。李辉等(2012)基于X12-ARIMA加法模型对我国保费收入月度数据进行季节调整，进而建立了我国保费收入的短期预测模型 [18]。刘红亮(2013)将重庆市月度保费收入序列中的循环因素、不规则变动、趋势因素以及季节因素分解出，然后建立相应的ARIMA模型对其进行短期预测分析 [19]。时间序列模型最大的优点在于操作简便，根据数据特征构造合适的滞后项模型并对参数加以估计就可以对目标序列做出预测。

近些年来，也有越来越多的学者将上述的各种定量分析方法结合在一起，脱离单一预测的形式，运用组合预测方法对我国保险业规模进行预测研究。陆秋君(2006)运用协整回归模型对影响我国保险业密度的相关因素进行了分解，之后通过建立Gompertz模型对我国保险业的短期发展趋势进行了预测 [20]。包慧敏等(2006)在运用多元回归模型的基础上，将指数平滑法加入其中，从而对内蒙古地区年度保费收入增长的趋势进行了预测 [21]。吕卓等(2016)创新性地采用组合预测的方法将回归模型、移动平均模型、时间序列模型、以及时间趋势模型的预测结果进行综合分析，构造出一个新的预测指标，进而更加精准的对我国“十三五”时期保险行业的保费收入进行预测 [22]。周桦等(2020)基于时间序列SARIMA模型对我国月度保费收入的主要趋势进行拟合，接着利用TEI@I方法论，设计了一个非线性集成预测模型，并利用该模型科学、严谨地分析了中国保费收入的大致变动趋势 [23]。组合预测法的优点在于突破了单一预测方法可能存在的局限性，在一定程度上能够更加清晰的反映数据变化特征。

综上所述，已有部分学者利用多种定量分析方法对我国保险业发展规模进行了预测，事实证明这些预测结果都较为符合现实情况。但需要指出的是，当前对我国保险业规模的预测大多选用保费收入这一基础指标，鲜少有学者从保险规模发展的广度和深度的角度进行更深层次的预测。因此，本文在已有文献的基础上，选取保险密度指标，基于时间序列模型对其进行预测，也即从保险业规模广度的视角对未来我国保险普及率进行度量分析，并结合数据特点挑选出相对最优模型。

3. 数据来源与预处理

3.1. 数据来源

本文选取1980~2019年我国保费收入和人口总量的时间序列数据，构造反映保险普及率的保险密度指标进行时间序列建模分析。数据主要来源于《中国统计年鉴》，部分数据摘自历年的中国银行保险监督管理委员会的年度统计信息。其中，保险密度指标等于我国保费收入与人口总量的比值。

3.2. 数据预处理

由1980~2019年保险密度原始序列数据可知，在1980年的保险密度为人均0.4660元，而到了2019年保险密度增长为3024.2788元/人，可见这几十年来我国保险普及率的增长速度之快。为了避免数据巨大波动带来的异方差等问题，本文对原始序列做对数化处理得到序列 $\ln bxmid{u}_t$ 以消除可能存在的异方差问题。

对1980~2019年我国保险业对数化的保险密度时间序列做平稳性检验、异方差检验以及纯随机性检验的预处理工作 [24]。

3.2.1. 平稳性检验

首先，利用R软件画出保险密度序列 $\ln bxmid{u}_t$ 的时序图，对原序列的平稳性做初步的判断，结果如下图1所示。图1显示，保险密度时间序列具有明显的上升趋势，因此，初步判定该序列是非平稳的。

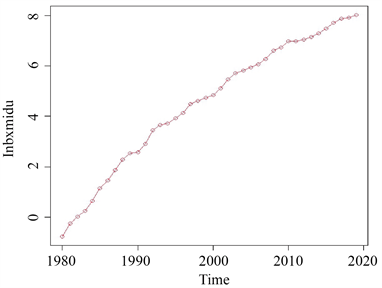
Figure 1. $\ln bxmid{u}_t$ sequence diagram

图1. $\ln bxmid{u}_t$ 序列时序图

其次，基于单位根检验对原序列的平稳性作进一步的分析。对 $\ln bxmid{u}_t$ 序列数据做ADF检验、PP检验，具体的检验结果如下表1所示。结果表明，上述两类单位根检验均不拒绝“H0：存在单位根”的原假设，也即进一步证实了我国1980~2019年保险密度时间序列具有非平稳性。

Table 1. Results of unit root test of original sequence

表1. 原始序列单位根检验结果

接着，由上述平稳性检验可知，我国1980~2019年保险密度的时间序列数据具有非平稳变化特征，因此，接下来需要对该序列进行差分处理以消除这种非平稳性。一阶差分后序列 $\nabla \ln bxmid{u}_t$ 的时序图如下图2所示。由时序图可知， $\nabla \ln bxmid{u}_t$ 序列已不具备明显的上升者下降的趋势，进而初步判断一阶差分后的保险密度序列平稳。

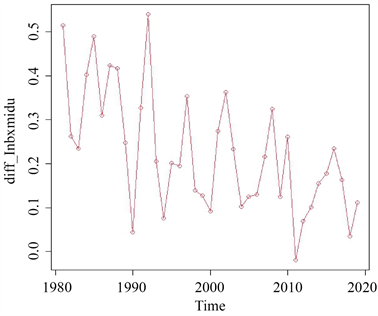
Figure 2. $\nabla \ln bxmid{u}_t$ sequence diagram

图2. $\nabla \ln bxmid{u}_t$ 序列时序图

最后，对一阶差分后的保险密度时间序列数据作进一步的平稳性检验。对该序列做ADF检验和PP检验，结果如下表2所示。结果表明，上述两类单位根检验均拒绝“H0：存在单位根”的原假设，也即进一步证实了一阶差分后的保险密度序列具有平稳的特性。

Table 2. Results of unit root test of ∇ ln b x m i d u t

表2. $\nabla \ln bxmid{u}_t$ 序列单位根检验结果

3.2.2. 自回归条件异方差检验

由图2 $\nabla \ln bxmid{u}_t$ 序列时序图可知，该序列在1990年前后存在上下较大的波动，合理怀疑 $\nabla \ln bxmid{u}_t$ 序列仍存在异方差问题，因此，对该序列做ARCH异方差检验，这里使用Portmanteau Q统计量来进行检验，检验结果如下表3所示。Portmanteau Q检验的结果表明残差序列显著方差齐性，因此，可认为 $\nabla \ln bxmid{u}_t$ 序列不存在异方差的问题。

Table 3. Results of heteroscedasticity test of ∇ ln b x m i d u t

表3. $\nabla \ln bxmid{u}_t$ 序列异方差检验结果

3.2.3. 纯随机性检验

通过上述平稳性检验的分析，得到了一组平稳的一阶差分保险密度时间序列，下面需要对其进行纯随机性检验，验证一阶差分后的序列各项之间是否还存在着相关性，若各项之间存在着相关性，说明有建模的必要性，否则，将不必对该序列进行后续的建模和预测工作。本文基于LB统计量对 $\nabla \ln bxmid{u}_t$ 序列进行纯随机性检验，检验的具体结果如下表4所示。

Table 4. Results of white noise test of ∇ ln b x m i d u t

表4. $\nabla \ln bxmid{u}_t$ 序列纯随机性检验结果

由上表4可知，在滞后6阶、12阶的情形下，P-value值均显著，因此拒绝原假设，认为一阶差分后的保险密度时间序列并不具有随机性，可以进行后续的建模和预测工作。

4. 模型的建立与预测

4.1. ARIMA模型的建立

对数据做完平稳性检验和纯随机性检验的预处理工作后，得到了一组可以进行建模的平稳的一阶差分保险密度时间序列，下面根据该序列的ACF图及PACF图对模型进行定阶，结果如下图3、图4所示。

下面根据序列的自相关函数图、偏自相关函数图的特征进行模型的识别以及定阶，可以尝试建立如下的5种ARIMA模型：ARIMA(0, 1, 4)模型、ARIMA(1, 1, 0)模型、ARIMA(1, 1, 4)模型、ARIMA(0, 1, 1)模型、ARIMA(1, 1, 1)模型，以及2种疏系数模型：ARIMA(0, 1, (1, 4))模型、ARIMA(1, 1, (1, 4))模型。利用R软件拟合以上七个模型，依据模型的显著性检验、参数的显著性检验以及AIC准则的结果进行综合性分析，最终选择一个相对最优模型来拟合序列，不同模型的拟合结果如下表5、表6所示。

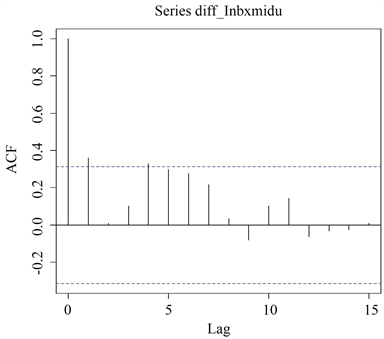
Figure 3. Autocorrelation function graph of $\nabla \ln bxmid{u}_t$

图3. $\nabla \ln bxmid{u}_t$ 序列自相关函数图

Figure 4. Partial autocorrelation function graph of $\nabla \ln bxmid{u}_t$

图4. $\nabla \ln bxmid{u}_t$ 序列偏自相关函数图

Table 5. Comparison of fitting results of ARIMA model

表5. ARIMA模型的拟合结果比较

注：***p < 0.01，**p < 0.05，*p < 0.1，括号内为标准误差。

由上表5的结果可知：根据df = 6的LB统计量的相伴概率值显示，仅ARIMA(0, 1, 1)模型的显著性检验未通过，因此，首先将该模型排除掉；ARIMA(1, 1, 4)模型和ARIMA(1, 1, 1)模型中，个别参数的显著性检验未通过；最后，比较以上模型的AIC值可知，ARIMA(1, 1, 4)模型对应的AIC值最小。因此，通过上述的综合分析认为ARIMA(1, 1, 4)模型能够更好地拟合一阶差分后的保险密度序列，又由于该模型的MA(3)项参数的显著性检验未通过，故将该项剔除在模型外，最终，ARIMA(1, 1, 4)模型的拟合结果为：

$\left(1-B\right)X_t=\frac{1+0.7647B+0.3190B^2-0.3643B^4}{1-0.9770B}{\epsilon }_t.$

Table 6. Comparison of fitting results of thinning coefficient model

表6. 疏系数模型的拟合结果比较

注：***p < 0.01，**p < 0.05，*p < 0.1，括号内为标准误差。

接着由上6的结果可知，两个模型均通过模型的显著性检验以及参数的显著性检验，且ARIMA(1, 1,(1, 4))模型的AIC值明显要更小。因此，通过上述的综合分析认为ARIMA(1, 1, (1, 4))模型能够更好地拟合一阶差分后的保险密度序列，最终，该模型的拟合结果为：

$\left(1-B\right)X_t=\frac{1-0.9125B-1.1260B^4}{1-0.4801B}{\epsilon }_t.$

下面对ARIMA(1, 1, 4)模型和ARIMA(1, 1, (1, 4))模型进行自回归条件异方差检验，仍然使用Portmanteau Q统计量，结果如下表7所示。结果表明，残差序列显著方差齐性，ARIMA(1, 1, 4)模型、ARIMA(1, 1, (1, 4))模型拟合成功。

Table 7. Results of autoregressive conditional heteroscedasticity test of ARIMA(1, 1, 4) and ARIMA(1, 1,(1, 4))

表7. ARIMA(1, 1, 4)模型、ARIMA(1, 1,(1, 4))模型自回归条件异方差检验结果

4.2. 模型的预测

上文已经挑选出拟合效果相对较好的ARIMA(1, 1, 4)模型以及ARIMA(1, 1, (1, 4))模型，下面利用这两个模型进行为期5年期的预测，然后对不同模型2020年、2021年的预测值与真实值进行比较，并计算相对误差，进而挑选出相对最优模型，得到的模型预测结果见下表8所示。

Table 8. Comparative analysis of model prediction results

表8. 模型预测结果比较分析

由上表8可知，相对而言，ARIMA(1, 1, 4)模型预测结果的相对误差都较大，而ARIMA(1, 1, (1, 4))模型的预测效果较好，相对误差集中在4.6%附近。因此，最终通过综合比较可知，ARIMA(1, 1, (1, 4))模型为我国保险密度年度数据的相对最优模型，利用该模型对保险密度序列作为其5年的预测图如下图5所示。

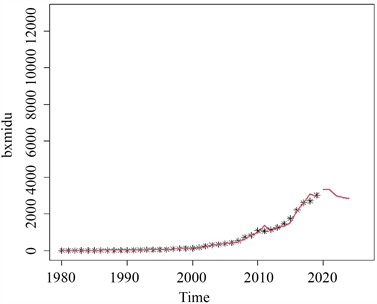
Figure 5. The prediction result of Chinese insurance density in the next five years

图5. 我国保险密度未来5年预测结果

5. 结论

本文基于时间序列模型对反映我国保险普及率的保险密度序列进行分析和预测，通过综合对比预设的几个模型的拟合精度以及预测的精度，选出拟合结果相对最优的ARIMA(1, 1, (1, 4))模型对未来5年我国保险密度进行预测，结果表明，该模型的预测效果最接近真实值，我国未来短期保险密度将呈现小幅度的下降趋势。