贮存剖面下考虑镀层厚度的电连接器接触性能退化模型研究

Study on Contact Degradation Model of Elec-trical Connectors Considering Plating Thickness under Storage Profile

摘要: 针对镀层厚度对电连接器接触件贮存可靠性的影响机制问题，分析了电连接器接触件在贮存剖面下的贮存应力及相应的接触失效机理，并基于Wiener过程建立了在温度应力下考虑镀层厚度的电连接器接触性能退化模型，量化了镀层厚度对接触件性能退化的影响程度；为了检验模型，设计了3组对比试验，对试验结果进行残差分析和正态性检验，结果验证了所建性能退化模型的正确性。运用扫描电镜对不同镀厚样品进行微观分析，验证失效机理分析和建模过程的合理性，证实镀金层厚度对接触性能退化的影响机制，进一步说明镀金层越厚越能有效延缓接触性能退化。为贮存剖面下的电连接器接触可靠性设计以及可靠性评估提供了理论基础。

Abstract: In view of the influence mechanism of plating thickness on the storage reliability of electrical con-nector contact parts, the storage stress and the corresponding contact failure mechanism of electri-cal connector contact parts under the storage section were analyzed. In addition, a contact perfor-mance degradation model of electrical connectors considering coating thickness under temperature stress is established based on the Wiener process, which is capable of quantifying the influence of coating thickness on the performance degradation of contacts. In order to test the model, three groups of comparative tests were designed, and residual analysis and normality test were conduct-ed on the test results. The results verified the correctness of the proposed performance degradation model. Scanning electron microscopy is leveraged to analyze various thickness samples to testify to the rationality of the failure mechanism analysis and modeling, confirm the influence mechanism of gold plating thickness on contact performance degradation, and further explain that the thicker the gold plating layer, the more effective it can serve as a decelerator to the contact performance deg-radation. It provides a theoretical basis for the contact reliability design and reliability evaluation of the electrical connector under the storage profile.

1. 引言

本电连接器在各类武器、航空航天等型号装备上大量使用，是实现装备内各部件之间电能、电信号传输的基础元件。同时电连接器也是系统内的薄弱环节之一，对型号装备的贮存可靠性有重要影响 [1] 。在长期的贮存环境下，电连接器的主要失效模式为接触失效。金作为稳定的惰性金属，几乎不随环境、时间变化，因此为了减缓环境应力和表面微观缺陷导致的接触性能退化，往往会在接触件的表面镀金。通过增大镀金层厚度，能有效减缓接触性能的退化速度。但是目前几乎没有镀金层厚度对贮存寿命影响的定量研究，无法通过确定镀金层厚度来评估贮存寿命。为此，考虑镀层厚度的电连接器接触性能退化模型研究很有工程价值及意义。

研究表明，镀层的厚度与质量对电接触性能有重要影响 [2] [3] 。尤其是镀层厚度会通过影响镀层表面的孔隙率、粗糙度、显微硬度等因素来影响电连接器接触件的接触性能。张义等 [3] 通过试验得出随着金层厚度增加，孔隙率下降，在厚度达到1.9 μm时，认为基本无孔隙。以及随着底镀层厚度增加，接触电阻有下降趋势。王思醇等 [4] 研究表明电接触转换器件的可靠性与镀层质量有关，以镀层的内应力、孔隙率为切入点，通过调整镀层结构可以提高产品性能。当然镀金层也不是越厚越好，芦娜等 [5] 提出镀金层过厚可能会出现由于镀层材料间的结合力下降导致的镀层剥落现象，不仅无法提高接触性能反而导致制造成本的增加。从这些研究可知，镀层厚度是电连接器接触件的一个重要设计参数，合理的选择镀层厚度对接触可靠性起关键影响。研究者们都致力于镀层结构对电接触性能影响的相关定性研究。但目前的研究依然存在问题：1) 镀层厚度对接触性能的影响机制尚未明确；2) 尚未定量的描述镀金层厚度对接触性能的影响程度。

本文以YF59-129型开槽收口式接触件为研究对象，分析氧化物堆积造成膜层电阻增长的失效机理，明确镀金层厚度对氧化物增长的影响机制，基于Wiener过程建立考虑镀金层厚度与温度环境应力的接触电阻性能退化模型，开展三个镀厚水平的加速退化试验，从数据分析和接触表面微观分析两个方面对模型的正确性进行检验。

2. 贮存剖面下接触件失效分析

2.1. 接触件失效机理

为了具有良好的导电性，并防止接触件表面的氧化和硫化腐蚀造成的接触不良，航天用电连接器的接触件一般采用青铜/黄铜作为基地材料，并在表面镀金。由于镀金层结晶成一种网状结构且厚度较薄，镀金层中不可避免地会出现一些微孔和裂纹。这些孔隙导致部分基体材料铜暴露于空气中，与氧气反应生成Cu₂O。

$4Cu+O_2=2C{u}_{2}O$

镀层表面的孔隙还会聚集环境中的水汽形成电解液环境，金属材料间的电位差导致在电解液环境下形成Au-Cu原电池。电解后的Cu⁺通过晶格缺陷快速通道 [6] 扩散至镀层表面，由于Cu⁺对氧气具有强烈的亲和力，易反应生成不导电的Cu₂O腐蚀物。

$4C{u}^{+}+O_2+4e^{-}\to 2C{u}_{2}O$

从微观层面看，基体表面Cu⁺、氧化物和氧化物表面O²⁻构成电容型双电层结构，Cu⁺的扩散依赖于双电层间的电场，氧化物越厚，电场强度越弱，Cu⁺扩散越困难，因此Cu₂O的增长随氧化膜厚度增加而受到抑制，氧化物生成速率随时间逐渐变缓。文献 [6] 证明200℃以下时，Cu₂O膜层厚度d的增长服从以下规律：

$d=k{t}^{\frac{\text{1}}{\text{3}}}$ (1)

式中，d为氧化膜层厚度；k为氧化腐蚀物体积增长系数；t为时间。

在长期贮存环境下随着Cu⁺不断扩散，绝缘氧化膜厚度持续增加，引起接触电阻逐渐增大，最终超过失效阈值发生接触失效。

2.2. 镀金层厚度对氧化物增长的影响

由上文可知，镀层的孔隙是氧化腐蚀物生成的主要诱因，则镀层表面孔隙的多少对氧化物增长速率起重要影响。而镀金层的孔隙率又与镀金层的厚度有关，镀金层越厚，孔隙率越低 [7] 。故以镀金层表面孔隙率为切入点，建立镀层厚度与氧化腐蚀物增长规律之间的关系。

相关研究 [8] 已给出了以单位面积上孔隙个数来定义的孔隙率表达式：

$P^{\prime }=\frac{b}{h^a}$ (2)

式中， $P^{\prime }$ 为个数比孔隙率，个/cm²；h为镀金层厚度，μm；a和b均为与镀金工艺有关的常数。

易见式(2)中，当镀层厚度h等于0时，个数比孔隙率 $P^{\prime }$ 趋于无穷，这与实际情况不符，因此个数比孔隙率不能较好描述当镀层厚度等于或趋近于0的情况。

本文以单位面积上的孔隙面积来定义孔隙率，记作面积比孔隙率P。由于目前关于面积比孔隙率的研究较少，故构造镀金层厚度h与面积比孔隙率P之间的拟合关系式：

$P={\left(\frac{b}{b+h}\right)}^a$ (3)

用相关实际面积比孔隙率研究数据 [9] 对所建面积比孔隙率表达式(3)进行拟合优度检验，如表1所示，决定系数 $R^2=0.995$ 接近于1，证明面积比孔隙率与镀层厚度之间的关系可用公式(3)进行描述。

Table 1. Goodness-of-fit test data table

表1. 拟合优度检验数据表

则接触表面上孔隙的总面积 $S_P$ 可由视在接触面积 $S_c$ 与面积比孔隙率P的乘积求得，即：

$S_P=P\cdot S_C={\left(\frac{b}{b+h}\right)}^a\cdot S_C$ (4)

由失效机理分析可知氧化腐蚀物主要在孔隙处生成，故氧化腐蚀物的总体积可认为是孔隙的总面积 $S_P$ 与膜层厚度d的乘积。结合式5和式1，可推得特定镀层厚度接触件的氧化腐蚀物体积增长规律：

$V\left(t\right)=k_T{\left(\frac{b}{b+h}\right)}^a{t}^{\frac{1}{3}}$ (5)

式中， $k_T=S_c\cdot k$ ，视在接触面积 $S_c$ 在插合贮存条件下保持不变， $k_T$ 主要受温度影响。

3. 接触性能退化模型建立

3.1. 氧化物体积与接触电阻的关系

接触件的接触电阻由体电阻 $r_V$ 、收缩电阻 $r_s$ 和膜层电阻 $r_f$ 组成。贮存剖面下接触电阻变化主要受膜层电阻影响，体电阻和收缩电阻均视为定值，故接触电阻r可表示为：

$r=r_0+r_f$ (6)

式中， $r_0=r_V+r_s$ 为定值。

根据电接触理论 [7] ，膜层电阻与膜层厚度的关系可表示为：

$r_f=\frac{\rho d}{S_a}=\frac{\rho d}{\pi a^2}$ (7)

式中， $\rho$ 为氧化腐蚀物隧道电阻率，d为膜层厚度， $S_a$ 为接触斑点总面积，a为接触斑点平均半径。

接触件表面是有一定粗糙度的，在微观层面可看作两个凹凸不平的表面，如图1所示，其中相互接触的部分便构成了接触斑点，只有当生成的氧化腐蚀物覆盖在接触斑点上时才会引起膜层电阻。

因此氧化腐蚀膜层厚度d可由覆盖在接触斑点上的氧化腐蚀物总体积公式推得：

$d=\frac{V_m}{S_a}=\frac{V_m}{\pi a^2}$ (8)

式中， $V_m$ 为覆盖在接触斑点上氧化腐蚀物总体积。

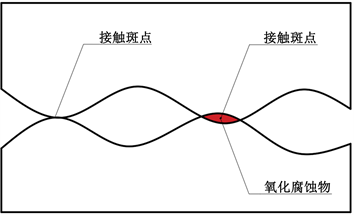
Figure 1. Micro schematic diagram of contact surface

图1. 接触表面微观示意图

为了更清晰地描述氧化腐蚀物是否覆盖在接触斑点上，可将插针与插孔的接触区域沿视在面展开，如图2所示。由于每个接触斑点和每份氧化腐蚀物在实际接触面所占的面积非常小，为便于研究可将其理想化视为圆，并随机分布在接触件表面。用两类圆的随机相遇模型来表征氧化腐蚀物随机覆盖在接触斑点上。

Figure 2. Unfolded drawing of contact surface

图2. 接触面展开图

假设有n份氧化腐蚀物覆盖在接触斑点上，此时覆盖在接触斑点上氧化腐蚀物总体积可表示为：

$V_n={\displaystyle \underset{i=1}{\overset{n}{\sum }}{v}_i=n\Delta v}$ (9)

式中， $v_i$ 是第i份氧化腐蚀物的体积， $\Delta v$ 为每份氧化物的平均体积。

将式(9)式(8)代入式(7)，推得n份氧化物覆盖在接触斑点上导致的膜层电阻为：

$r_f=\frac{n\rho \Delta v}{{\left(\pi a^2\right)}^2}$ (10)

3.2. 考虑镀厚的接触件性能退化模型

电连接器接触件一经插合，所有接触斑点的分布位置即确定，因此可认为在长期插合贮存的情况下所有接触斑点的位置保持不变。此时整个接触展开面分为由接触斑点组成的接触斑点区域以及其他非接触斑点区域如图3所示。进而可通过第i份氧化物是否落入接触斑点区域来判断氧化物是否覆盖在接触斑点上，并记作事件 $X_i$ ，氧化腐蚀物落入接触斑点区域时 $X_i=1$ ，氧化腐蚀物落入非接触斑点区域时 $X_i=0$ 。

Figure 3. Schematic diagram of probability model principle

图3. 概率模型原理示意图

则 $X_i$ 服从0~1分布，表示为：

$X_i=\{\begin{array}{cc}1,& p\\ 0,& 1-p\end{array}\begin{array}{cc}& i=0,1,2,\cdots ,n\end{array}$ (11)

其中，氧化腐蚀物覆盖接触斑点的概率p为接触斑点区域面积 $S_a$ 与视在面积 $S_c$ 的比值。

此时覆盖于导电斑点区域的氧化物总体积 $S_n$ 可表示为：

$S_n=\Delta v{\displaystyle \underset{i=1}{\overset{n}{\sum }}{X}_i}$ (12)

为进一步描述覆盖到接触件接触斑点上氧化腐蚀物的量，构造随机变量 ${\tilde{X}}_i=\Delta v\left(X_i-p\right)$ 。可求得随机变量 ${\tilde{X}}_i$ 的均值和方差为：

$E{\tilde{X}}_i=0;Var{\tilde{X}}_i=\Delta v^2\left(p-p^2\right)$ (13)

由于每个氧化腐蚀斑点之间相互独立， $\left\{{\tilde{X}}_n\right\}$ 为独立同分布的随机变量列，通过独立同分布列 $\left\{{\tilde{X}}_n\right\}$ 可构造含有所需变量 $S_n$ 的部分和序列 $\left\{{\tilde{S}}_n\right\}$ ，表示为：

${\tilde{S}}_n={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\tilde{X}}_i={\displaystyle \underset{i=1}{\overset{n}{\sum }}\Delta v\left(X_i-p\right)=\Delta v{\displaystyle \underset{i=1}{\overset{n}{\sum }}{X}_i-n\Delta vp}}}=S_n-n\Delta vp$ (14)

将该随机序列映射至区间 $\left[0,1\right]$ ，可得随机元列 $\left\{{\tilde{W}}_n\right\}$ ：

${\tilde{W}}_n\left(t,\omega \right)=\{\begin{array}{ll}\frac{{\tilde{S}}_i\left(\omega \right)}{\sqrt{nVar{\tilde{X}}_i}}\hfill & t=\frac{i}{n},i=0,1,\cdots n\hfill \\ 线性\hfill & \frac{i-1}{n}\le t\le \frac{i}{n}\hfill \end{array}$ (15)

式中， $\omega$ 是 ${\tilde{S}}_i$ 所对应的事件。

在满足式(13)与式(15)的情况下，由泛函中心极限定理 [10] 可得 $\left\{{\tilde{W}}_n\right\}$ 依分布收敛于维纳过程，表示为：

${\tilde{W}}_n\stackrel{d}{\to }W$ (16)

则

$\frac{{\tilde{S}}_n}{\sqrt{nVar{\tilde{X}}_i}}=\frac{S_n-np\Delta v}{\sqrt{nVar{\tilde{X}}_i}}\stackrel{d}{\to }W$ (17)

根据维纳过程的平移不变性和尺度不变性，对式(17)作变换，可得覆盖于导电斑点区域的氧化物总体积 $S_n$ 亦可由维纳过程描述：

$S_n\stackrel{d}{\to }n\Delta vp+W\left(nVar{\tilde{X}}_i\right)$ (18)

式中， $p=S_a/S_c$ ， $n\Delta v=V\left(t\right)=k_T{\left(\frac{b}{b+h}\right)}^a{t}^{\frac{1}{3}}$ 为n份氧化物在t时刻积累的氧化物总体积。

结合式(5)、式(13)和式(18)可得膜层电阻 $r_f$ 的表达式为：

$r_f=\frac{\rho }{{\left(\pi a^2\right)}^2}p{k}_T{\left(\frac{b}{b+h}\right)}^a{t}^{\frac{1}{3}}+W\left(\frac{{\rho }^2}{{\left(\pi a^2\right)}^4}\Delta v\left(p-p^2\right)k_T{\left(\frac{b}{b+h}\right)}^a{t}^{\frac{1}{3}}\right)$ (19)

为简化模型，可令

$\begin{array}{l}{\mu }_T=\frac{\rho }{{\left(\pi a^2\right)}^2}p{k}_T;\\ {\sigma }_T^2=\frac{{\rho }^2}{{\left(\pi a^2\right)}^4}\Delta v\left(p-p^2\right)k_T\end{array}$ (20)

代入式(19)，可得温度应力下考虑镀层厚度的电连接器接触件性能退化模型：

$r\left(t|h\right)=r_0+{\mu }_T{\left(\frac{b}{b+h}\right)}^a{t}^{\frac{1}{3}}+{\sigma }_T{\left(\frac{b}{b+h}\right)}^{\frac{a}{2}}W\left(t^{\frac{1}{3}}\right)$ (21)

其中， ${\mu }_T$ 和 ${\sigma }_T$ 受温度应力水平影响，可采用Arrhenius方程进行描述，即：

${\mu }_T=\exp \left(c+dx\right)$ (22)

${\sigma }_T=\exp \left({\gamma }_0+{\gamma }_{1}x\right)$ (23)

式中，温度应力水平 $x=\frac{1000}{273.15+T}$ 。

4. 模型验证

4.1. 试验方案

选取YF59-129型开槽收口式接触件作为试验样品。参考常见接触件镀厚值，设置两个不同镀厚水平的组别进行试验，两组镀层厚度水平分别为1.0 μm和1.4 μm，并额外增设一组0 μm作为参照组。每组投放5对接触件，共投放15对接触件。根据现有研究 [11] [12] ，158℃下电连接器接触件失效机理并未发生改变，能起到较好的加速效果。且设置一组温度应力水平能够满足研究需求，为降低试验成本，本文选择仅在158℃下开展试验。测试时间间隔定为24小时，测试指标为接触电阻。由于接触电阻阻值为毫欧级别，为消除导线阻值的干扰，采用“开尔文四端线法”进行测量 [13] 。

最终试验方案如表2所示。

Table 2. Constant stress accelerated test scheme of contact

表2. 接触件恒定应力加速试验方案

4.2. 性能退化模型验证

4.2.1. 试验数据

按照试验方案，对不同镀厚组的接触件样品进行定时接触电阻测试，得到158℃下0 μm，1.0 μm和1.4 μm三组的接触电阻性能退化轨迹箱线图，如图4所示。

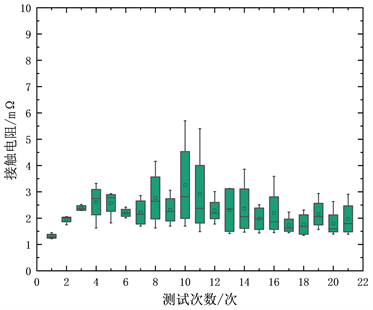(a) 镀层厚度0 μm (b) 镀层厚度1.0 μm 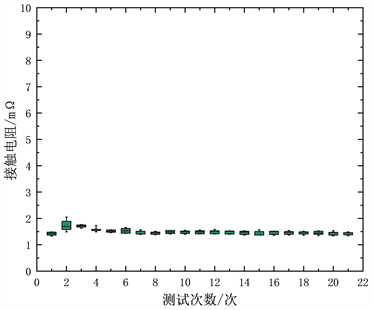(c) 镀层厚度1.4 μm

Figure 4. Box diagram of contact performance degradation of each coating thickness group at 158˚C

图4. 158℃下各镀厚组接触性能退化轨迹箱线图

从图中可以看出，在镀金层厚度为0 μm时，接触电阻增长速率较快；镀金层厚度为1.0 μm时，接触电阻增长速率减缓，对接触件已经能起到较好的保护作用；镀金层厚度为1.4 μm时，接触电阻增长十分缓慢。各组样品的接触电阻随时间均呈非线性波动增长的趋势，这一特点与Wiener过程漂移参数的描述相一致。并且接触电阻的增长随着镀金层的增厚具有明显的减缓，即镀金层越厚，漂移系数越小。

4.2.2. 残差分析

计算不同镀厚组的接触电阻残差，并绘制如图5所示的残差箱线图。可见各组接触件随着试验进行，所测接触电阻的波动程度逐渐增大，趋势基本呈现“喇叭口”形状，与维纳过程扩散系数的描述一致。初步说明维纳过程模型的适用性与正确性。同时镀层越厚，波动程度越小，扩散系数越小，说明镀金层能明显抑制接触电阻的波动。

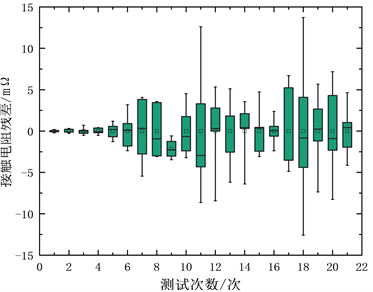(a) 镀层厚度0 μm (b) 镀层厚度1.0 μm (c)镀层厚度1.4 μm

Figure 5. Contact resistance residual box diagram of each plating thickness group at 158˚C

图5. 158℃下各镀厚组接触电阻残差箱线图

4.2.3. 正态性检验

由Wiener过程性质 [14] ，在漂移系数、扩散系数为常数时，相同温度、相同测试间隔、同组的样品的接触电阻增量 $\Delta r$ 应当服从正态分布：

$\Delta r~N\left({\mu }_T{\left(\frac{b}{b+h}\right)}^a\Delta t^{\frac{1}{3}},{\sigma }_{T,h}^2{\left(\frac{b}{b+h}\right)}^a\Delta t^{\frac{1}{3}}\right)$ (24)

因此本文采用Epps-Pulley数值检验 [15] 对模型进行正态性检验，检验结果如表3所示。由于三组的检验统计量 $T_{EP}$ 均小于在显著性水平 $\alpha =0.05$ 下Epps-Pulley检验统计量的分位数 $T_{0.95}$ ，可认为接触件的接触电阻增量服从正态分布，即证明式(17)的正确性。

Table 3. Test results of contact resistance increment normality

表3. 接触电阻增量正态性检验结果

4.3. 失效机理验证

运用扫描电镜对试验后的样品表面进行观测，如图6所示，在接触件的表面可以观测到镀金层表面存在明显的划痕与孔隙，同时附近也存在堆积的块状氧化腐蚀物，进而验证了上文中失效机理分析的合理性。但模型计算相较于实际情况更为理想化，两者之间依旧存在一定的差异。在建模过程中，本文假设氧化腐蚀物在孔隙处堆积并依据孔隙面积来求解膜层厚度，但在电镜实验结果中可以发现部分氧化腐蚀物并不是完全覆盖堆积在孔隙上，而是在孔隙的附近堆积；基于氧化腐蚀斑点与接触斑点随机相遇的机制统计建模过程中，将氧化腐蚀斑点理想化为圆，而在电镜观测结果中，可以发现氧化腐蚀物的形状是不规则的，往往与孔隙的形状有关，例如在划痕处的堆积物呈现条状，孔洞处呈现半球状。

Figure 6. Micro defects of contact surface

图6. 接触表面微观缺陷

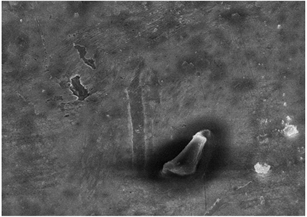
对比1.0 μm镀厚组和1.4 μm镀厚组的微观表面，如图7所示，1.0 μm镀厚组的接触件表面缺陷更为严重，具有较多的腐蚀物堆积，说明在镀层较薄时，表面孔隙多易发生氧化腐蚀。1.4 μm镀厚组表面相对光滑，仅存在少许细微孔隙，镀金层能有效隔绝了基底材料与氧气接触，证明增加镀金层厚度对防止接触件表面退化具有明显作用。

(a) 镀层厚度1.0 μm (b) 镀层厚度1.4 μm

Figure 7. Contact surface comparison diagram

图7. 接触表面对比图

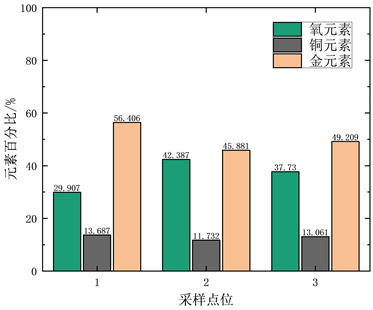
分别在1.0 μm镀厚组和1.4 μm镀厚组接触件表面各随机取三个点做能谱分析，对比接触件不同位置的Cu、O、Au的成分，结果如图8所示。对于同一镀金层厚度，不同采样点位，O元素和Cu元素的含量各不相同，证明氧化腐蚀物并不是以膜层的形式均匀依附在接触件表面，而是以堆积物的形式随机生成在接触表面，进而验证了上文接触斑点与腐蚀物斑点随机相遇的建模思路合理。1.0 μm镀厚组的O、Cu含量均高于1.4 μm镀厚组，但Au含量均低于1.4 μm镀厚组，再一次说明镀层较薄的组氧化腐蚀更为严重，证明镀金层厚度会影响接触件的氧化腐蚀，验证上文的失效分析与镀层影响分析的正确性。

(a) 镀层厚度1.0 μm (b)镀层厚度1.4 μm

Figure 8. Element content comparison

图8. 元素含量对比图

5. 总结

1) 本文基于贮存剖面下的失效机理，构造镀金层厚度与孔隙率的定量表达式，建立了温度应力条件下考虑镀金层厚度的电连接器接触性能退化模型，所建模型为包含镀层厚度这一设计参数的非线性Wiener过程，充分反应了镀金层厚度对电连接器接触性能退化的影响。

2) 开展了不同镀层厚度下的接触件恒定应力加速试验，通过残差分析和正态性检验，其结果符合Wiener过程的定义，证明了所建模型的正确性。通过微观表面分析和元素含量分析，验证镀金层厚度对接触件性能退化的影响机制。

3) 本文所建立的考虑镀层厚度的电连接器接触性能退化规律，为电连接器接触件的可靠性设计，可靠性增长及可靠性评估等提供一定的理论基础和参考价值。

基金项目

浙江省重点研发计划项目(项目号：2021C01133)；NSFC-浙江两化融合项目(项目号：U1709210)；浙江省重点研发计划项目(2019C03108)。