1. 引言
近年来,视频合成孔径雷达(Video Synthetic Aperture Radar, ViSAR)由于其自身优势受到了越来越多的关注。其能够实现对感兴趣区域(Regin of interest, ROI)的连续视频观察,在雷达平台飞行过程中以一定帧率将获得的一系列图像以视频形式播放。ViSAR使得SAR图像由“静态”向“动态”发展 [1] ,通过提高图像帧率可以实现对运动目标的持续跟踪,获得速度、运动方向等更丰富的场景信息 [2] 。ViSAR系统同时继承了传统SAR的优势,即不易受天气、环境等条件的影响,可以全天时、全天候工作,且分辨率高、穿透性强 [3] [4] 。随着对太赫兹(Terahertz, THz)波的研究 [5] - [11] ,工作于太赫兹波段的THzViSAR由于能够快速实现高分辨成像受到了越来越多的关注,并且在军用、民用等领域拥有广阔的应用前景和强大的发展潜力。
目前经典的成像算法包括后向投影算法(Back Projection Algorithm, BPA) [12] 和极坐标格式算法(Polar Format Algorithm, PFA) [13] 。BPA从时域逐脉冲积累能量,可以在任意成像网格上进行图像重建,具有精确的运动补偿能力,理论上适用于任意轨迹、任意成像模式,但其极高的运算复杂度严重限制了该算法的广泛应用。后来,学者们相继研究并提出了多种加速算法 [14] - [22] ,其中最为经典的是快速多级后向投影算法(Fast Factorized Back Projection Algorithm, FFBPA) [16] 。该算法将全孔径划分为若干子孔径,并在局部极坐标系下进行逐级相干积累,使得算法效率得到显著提高。然而,FFBPA通过大量的二位插值操作实现不同局部极坐标系之间的映射,这将不可避免地导致插值误差的引入和积累,并最终影响图像质量。为减小插值误差可增加子孔径长度,但由于FFBPA在初始阶段仍采用了低效的BP积分进行子图像重建,子孔径长度的增加会导致算法运算量的增加,并不断向传统BPA逼近;也可以通过提高插值核精度来减小插值误差,但这也将加大算法实现难度及运算量。因此,在实际应用中FFBPA难以兼顾图像质量和运算效率,通常会牺牲一部分图像质量以达到更高的运算效率。
PFA是一种高效的频域成像算法,且更适用于ViSAR成像。该算法基于平面波前假设,算法步骤简单,计算量小。但是其缺陷也正是因为采用了平面波前假设,引起了残余相位误差,主要包括线性相位误差(Linear Phase Error, LPE)和二次相位误差(Quadratic Phase Error, QPE)。前者会导致几何失真,即目标不会出现在PFA图像的实际位置;后者会引起图像散焦,且离场景中心越远的目标散焦越严重,进而导致有效场景半径受到限制。与传统波段相比,太赫兹ViSAR具有更大的QPE容许半径,因此可以忽略该误差引起的散焦。然而,LPE与雷达工作频段无关,只与成像几何模型有关,所以该误差不可忽视。同时,对于ViSAR图像来说,每一帧图像都应该建立在同一地面坐标系中。因此,本文针对传统PFA中存在的LPE给出了有效的校正方法,同时将不同帧图像旋转至同一坐标系中,最后通过仿真实验进行验证。
2. 成像算法介绍
2.1. ViSAR回波模型
ViSAR典型的工作模式是圆周聚束模式,即雷达平台做匀速圆周运动,且波束始终指向固定的成像区域。在该模式下,雷达可以对成像区域进行持续监测,在短时间内生成一系列图像并以一定帧率进行视频播放。该成像几何构型如图1所示,以场景中心为原点O建立三维直角坐标系,H为雷达平台飞行高度,
和
分别为俯仰角和方位积累角,
表示雷达到场景中心的斜距。
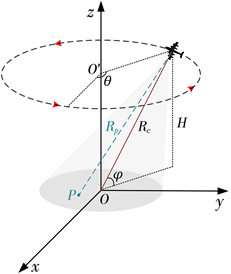
Figure 1. ViSAR imaging geometric model
图1. ViSAR成像几何模型
若以
表示雷达平台的瞬时位置,则根据几何关系,可以写为
(1)
天线发射大时宽带宽积的线性调频(Linear Frequency Modulation, LFM)信号 [23] ,其频率在一定时间内连续线性变化,如(2)所示。
(2)
其中,
为距离向快时间,
为矩形窗函数,
为脉宽,
为中心频率,调频率
,B为带宽。对于照射场景内任意点
,雷达到该点目标的瞬时斜距为
(3)
则该点目标的回波信号可以表示为
(4)
其中,
为方位向慢时间,从发射信号到接收回波之间的双程时延
,c为光速。
由于LFM信号的特殊性质,可以通过去调频(Dechirping)的方式对(4)进行脉冲压缩。通过选用一频率、调频率相同的LFM信号作为参考信号与回波信号进行差频处理,不仅运算简单,而且处理后的信号带宽大幅降低,进而减小雷达接收机的处理压力。
针对(4)所示的回波信号,并结合图1所示的几何构型,选取参考距离
,且调频率和中心频率相同的LFM信号作为参考信号,即
(5)
其中,
是参考信号的脉宽,一般略大于
,参考距离的双程时延
。
将回波信号(4)和参考信号(5)进行混频,即
,得到的差频信号为
(6)
其中,差分距离
。
2.2. 极坐标格式算法
极坐标格式算法(PFA)是一种典型的用于聚束模式的成像算法,该算法简洁高效,其处理流程如下。首先,将(6)做距离向傅里叶变换,得到距离频域信号(7)。
(7)
其中,
为距离向频率。
上式中的第二、三个相位项分别是斜置项和剩余视频相位(Residual Video Phase, RVP),需要将这两项进行去除,称为“去斜”操作。通过在距离频域乘以补偿函数(8)进行去除。
(8)
再进行距离向逆傅里叶变换,得距离时域信号如下
(9)
其中,波数
,且
可以重写为
(10)
基于平面波前假设对其进行泰勒展开,得到
(11)
则式(9)可以改写为
(12)
其中,距离向波数
和方位向波数
分别表示为
(13)
由式(13)可以看出,波数域采样点是分布在极坐标上的,需分别进行距离向插值和方位向插值使波数域采样点均匀地分布在直角坐标系中,该过程如图2所示。之后通过二维逆傅里叶变换即可得到PFA成像结果
。
(14)
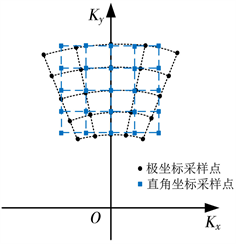
Figure 2. Coordinate transformation in wave number domain
图2. 波数域的坐标转换
3. 几何失真校正原理
3.1. 误差分析
平面波前假设是指远场情况下各阵元到点辐射源的射线近似为平行线,波前近似为平面波。然而实际波前是球面波,PFA在平面波前假设的基础上将
展开为(11),这将不可避免地导致线性和二次相位误差的存在。线性相位误差(Linear Phase Error, LPE)会导致图像失真,具体表现为PFA图像中的目标位置出现偏移;而二次相位误差(Quadratic Phase Error, QPE)会使图像发生散焦。本节将对PFA中存在的误差进行分析。
根据(9),相位
可以表示为
(15)
其中,
可以分解为两个正交分量
和
。因此,式(15)可以改写为二维波数域中心即
处的泰勒级数展开,得到
(16)
其中,C为常数项,
、
为一阶项系数,
、
为二阶项系数,
为交叉项系数。根据几何关系进行推导可以得到
(17)
其中,
。此时,一阶项系数
、
对应了目标在PFA图像中的几何位置,即
(18)
这意味着场景内目标位置发生偏移,且分布在一块扇形区域内。定义
为点目标真实位置
和偏移位置
之间的距离误差。图3所示为整个场景内的距离误差,图中分别绘制了距离误差为1 m和0.1 m的等高线。不难发现,离场景中心越远距离误差越大,也就是说离场景中心越远的目标偏移越明显。该几何失真情况是由LPE引起的,而LPE与雷达工作频段无关,只与成像几何构型有关,所以该误差不可忽视,须对其进行校正。

Figure 3. Range error in 300 GHz PFA image
图3. 300 GHz PFA图像距离误差
二阶项系数
、
是空变项,会导致图像发生散焦,且越靠近成像场景边缘,散焦就会越严重。因此,PFA的有效场景半径受到限制,且最大允许半径表示为
(19)
其中,
是理论方位分辨率,
是以
作为允许误差范围时的最大场景半径。不难看出,PFA的有效场景半径与波长
的开方成反比,即和中心频率
的开方成正比。对于斜距
、理论方位分辨率
、工作频率
的THzViSAR而言,其有效场景半径可达100 m。而THzViSAR成像区域小(如成像半径为60 m),QPE可以忽略,即认为场景内所有目标聚焦效果良好。
3.2. 几何失真校正原理
经分析,由于THzViSAR成像区域小、有效场景半径大的特点,可忽略QPE引起的散焦情况;而LPE与成像几何构型有关,与目标所在位置的横纵坐标有关,因此必须在图像域对该误差进行校正。该过程可以通过二维重采样实现,校正原理如图4所示,具体处理步骤如下:
1) 如图4所示,在地面xy坐标系中建立并划分校正网格,相邻校正点之间的横向和纵向间隔分别为
、
;

Figure 4. Principle of geometric distortion correction
图4. 几何失真校正原理
2) 针对每个校正点
,根据(18)计算其在PFA图像中的坐标
,完成几何失真映射;
3) 由该偏移坐标在PFA图像中通过插值找到其“像”,并将其返回校正点。该过程通过双线性插值实现,其核心思想是在两个方向上分别进行线性插值。如图5所示,已知
、
、
、
,那么
的值为
(20)

Figure 5. Principle of bilinear interpolation
图5. 双线性插值原理
4) 这样就完成了单个校正点的校正。重复以上步骤,直至完成校正区域中所有点的校正。
THzViSAR成像过程中,不同帧坐标系下获得的图像之间存在旋转,为了实现对同一块照射场景的持续观察,需将所有图像重建在统一的地面坐标系中。此时,可以在完成几何失真校正的同时完成图像的旋转,其实现过程如图6所示。首先将地面坐标系中的校正点
通过公式(21)进行旋转(其中
为旋转角度),再根据公式(18)进行几何失真映射,最后通过插值找到其“像”并返回校正点。综上所述,该几何失真校正流程如图7所示。
(21)

Figure 6. Geometric distortion correction combined with rotation
图6. 含图像旋转的几何失真校正

Figure 7. Flow chart of image correction
图7. 图像校正流程图
4. 仿真数据处理
为了验证PFA图像的几何失真校正效果,本节进行了点目标仿真实验,仿真参数设置如表1所示,仿真点目标分布如图8所示。在该参数条件下,PFA有效场景半径为100 m,成像区域范围未超过有效场景大小限制,因此仅考虑LPE引起的点目标位置偏移的校正。

Table 1. Simulation parameters setting
表1. 仿真参数设置
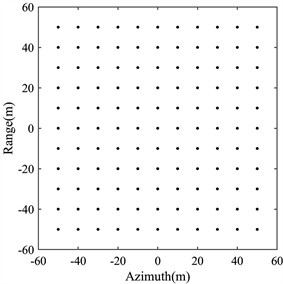
Figure 8. Simulation point target distribution
图8. 仿真点目标分布
采用本文所述的几何失真校正方法进行校正,得到的仿真结果如图9所示。其中图(a)为PFA算法成像结果,红点表示各点目标理论偏移位置,白点为实际成像位置,两者之间虽然存在误差,但可以接受。不难看出PFA图像中确实存在目标位置偏移,具体表现为点目标分布在一片扇形区域内;图(b)为几何失真校正结果,红点表示各点目标理论位置,白点为校正后的位置。从图中可以粗略地看出,本文所述的几何失真校正方法可以有效校正PFA中存在的线性相位误差(LPE)。
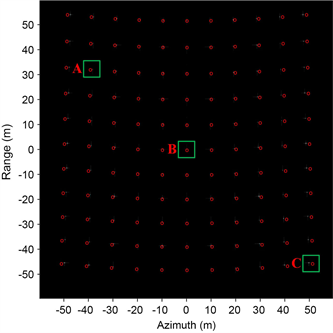 (a) PFA图像
(a) PFA图像 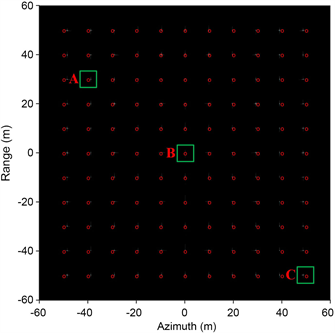 (b) 几何失真校正结果
(b) 几何失真校正结果
Figure 9. Imaging and geometric distortion correction results
图9. 成像及几何失真校正结果
为了进一步分析校正精度,表2给出了图像中A、B、C三个点目标的定位结果。从中可以看出,校正前的PFA图像中点目标存在较明显的偏移情况,而经过校正后,点目标位置能够有效且较精确地定位在其实际位置处。
同时,本文考虑了由不同帧坐标引起的图像旋转情况的校正,这里考虑的旋转角度为45˚,此时得到的仿真结果如图10所示,同样地用红点绘制了理论位置。其中图(a)为PFA算法成像结果,不难看出PFA图像中不但存在几何失真,同时存在旋转;图(b)为校正结果,从图中可以看出,本文所述的校正方法可以有效校正该旋转及几何失真情况。

Table 2. Geometric distortion correction results
表2. 几何失真校正结果
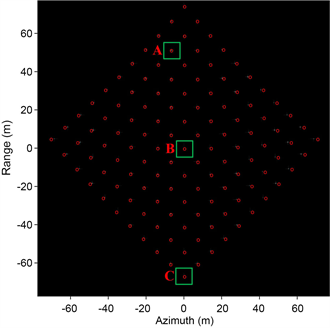 (a) 含旋转的PFA图像
(a) 含旋转的PFA图像 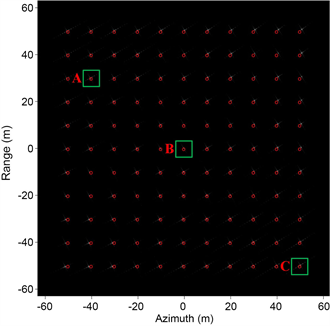 (b) 校正结果
(b) 校正结果
Figure 10. Imaging and correction results with rotation
图10. 含旋转的成像及校正结果
为了进一步验证校正效果,表3同样给出了A、B、C三个点目标的定位结果。从中可以看出,校正前的PFA图像中点目标位置严重偏移,而经过校正后的点目标能够有效且精确地位于在其实际位置处。

Table 3. Correction results with rotation
表3. 含旋转的校正结果
5. 结论
本文基于THzViSAR成像区域小、有效场景范围大的特点,同时考虑到不同帧坐标下的图像旋转,提出了一种图像域二维重采样的方法,完成对PFA图像的几何失真校正和旋转,将每帧图像重建在同一地面坐标系中。仿真结果表明,文中所提出的方法能够有效地校正PFA图像中存在的几何失真情况及旋转情况,验证了本文方法的可行性。因此该方法在THzViSAR高分辨连续成像中具有广泛的应用前景。
NOTES
*通讯作者。