一种基于牛顿法的约束最短路问题算法

An Algorithm Based on Newton Method for Constrained Shortest Path Problem

摘要: 针对通信网络中常见的信息传输路径规划问题，即约束最短路问题(Constrained Shortest Path, CSP)，由于该问题为NP-难问题，我们通过求解其拉格朗日对偶问题给出CSP问题的解。在求解对偶问题过程中，我们首先对于对偶问题的可行域进行限制，创新性地构造出了更紧的上界。其次，根据问题的特殊性，本文给出了求解对偶问题的新算法及牛顿迭代格式。其中每次迭代求解最短路问题，并通过所求的最短路径构造出对偶问题目标函数的梯度信息。此外我们采用超参数H来近似分段线性凸函数的二阶导数，从而构造出了牛顿迭代格式。新算法的数值实验表现出其求解CSP问题及其对偶问题的优势。

Abstract: Aiming at the information transmission path planning problem in communication networks, that is, the constrained shortest path problem, since the CSP problem is an NP-hard problem, we give the solution of the CSP problem by solving its Lagrange dual problem. In the process of solving the dual problem, we first limit the feasible fields of the dual problem and innovatively construct a tighter upper bound. Secondly, according to the particularity of the problem, a new algorithm for solving dual problems and Newtonian iteration format are given. Each iteration solves the shortest path problem, and constructs the gradient information of the objective function of the dual problem through the shortest path sought. In addition, we use the hyperparameter H to approximate the second derivative of the piecewise linear convex function, thus constructing the Newtonian iteration format. The numerical experiments of the new algorithm show its advantages in solving CSP problems and their duality problems.

1. 引言

随着通信网络的快速发展，用户对于信息传输需求也越来越高，通信正朝着低时延，大带宽的方向发展。由于传统的信息传输技术主要依赖于已有的路由协议进行，随着业务数的增多和信息交互频率的增加，传统技术会出现一系列的问题，如网络链路拥塞、传输时延过较大等。此外，在实际的通信网络路由中，常常要考虑网络的各个指标要满足一定要求，比如链路带宽有容量约束，总的端到端的传输时延和丢包率有上限约束等。在计算机硬件性能有限，而且网络规模以及数据传输需求较大时，快速而且高精度的路由算法显得尤为重要。传统的最短路算法在处理大规模路由问题仍然较为高效，但是该类算法只能处理网络权重固定，而且只有单一权重的问题。对于多个权重的路由问题来说，现存的算法仍然存在很多优化空间，比如精确算法时间复杂度过高，启发式算法难以给出解的质量保证等方面。在一定理论保证下，得到时间消耗较少而且质量较高的解是我们主要研究的出发点，因此，考虑在现行网络中的快速且高效的路由传输算法是一个现实问题。

通信网络中最短路问题是信息传路由选择的最基本问题之一，Dijkstra针对非负链路权重的网络中端到端最短路问题提出了多项式时间复杂度的求解算法，被称作Dijkstra算法 [1] 。在当下的更高带宽、业务更频繁的通信网络中依然作为最基本的路由算法被广泛的使用。而约束最短路问题是在满足一定线性约束条件下寻找端到端的最短路径，这类问题被证明是NP-难问题。针对约束最短路问题，有以下几类求解方法，启发式方法在求解速度上有明显优势，但解的质量不够稳定；精确算法则会消耗过多的计算资源，信息传输的时效性不够；此外，有一类基于拉格朗日对偶理论的求解算法，通过求解约束最短路问题的对偶问题，从而解决原问题，这类方法通常可以为原问题提供具有理论保证的近似解，在一些特殊问题中可以直接得到约束最短路问题的最优解。本文采用这种求解思路来解决约束最短路问题，并给出了一种全新的对偶问题的求解方法：基于牛顿法的约束最短路问题算法。利用约束最短路问题的特点给出对偶问题最优解的初始上界和下界，再利用牛顿法给出新的迭代点，利用Dijkstra算法求解最短路并通过其可行性更新上届或下届。

考虑CSP问题，给定网络拓扑图G (V, E)，V表示图上的所有节点构成的集合，E表示图上的所有的边构成的集合，给定起点s和终点t。对于图的每一条边上有两个权重，(例如：(c(e), d(e))， $\forall e\in E$ 表示边e上的费用和时延)。CSP问题是找到一条路径使得其中一个权重最小(如 $c\left(p\right)={\displaystyle {\sum }_{e\in p}c\left(e\right)c\left(p\right)}={\displaystyle {\sum }_{e\in p}c\left(e\right)c\left(p\right)}={\displaystyle {\sum }_{e\in p}c\left(e\right)}$ )，同时另一个权重不超过给定的阈值Δ (如 $d\left(p\right)={\displaystyle {\sum }_{e\in p}d\left(e\right)}\le \Delta$ )。针对CSP问题的求解算法主要包括精确算法、近似算法、启发式算法以及基于拉格朗日松弛的求解算法。

2. 背景

2.1. 相关工作

精确算法：解决CSP问题的精确算法可以采用系统地测试每一条路径进行检查(枚举)，但其中最大的问题就是路径数会随着问题的规模变大而指数增长，所以该方法的应用性并不强。Widyono等人提出了(Constrained Bellman-Ford) CBF算法 [2] ，可以找到从一个起点到多个终点的独立极小成本路径。主要思想是随着时延的递增，系统地发现最小成本路径。另外，伪多项式时间算法也可以作为一种精确算法。

伪多项式时间算法可以解决一个整数约束的最短路问题，这里给出的伪多项式时间按算法可以看作是EBF (Extended Bellman-Ford) [3] 算法的特殊形式，即不包含负权重的情形，最外层循环只有一次。其算法复杂度也对应为O(ΔE)。EBF算法的复杂度为O(ΔVE)，EDSP (Extended Dijkstra Shortest Path)算法 [3] 复杂度为O(Δ²V²)。如果网络比较稀疏，尤其Δ较大的情况下，该算法比EDSP算法 [3] 在理论上有更好的性能。

启发式算法：由于CSP问题是NP-困难的，所以一般来讲不存在多项式时间的精确算法进行求解，实际应用中，为了得到更快的计算效果，启发式搜索算法由于其执行时间较短，而且通常有较好的求解质量，所以经常被使用。H_MCOP (Heuristic Mulit-Constrained Optimal Path) [4] 算法用非线性费用权重来处理多个约束，其复杂度与Dijkstra算法同阶，具有较快的求解速度，但不保证求解成功。

其他方法：Jaffe [5] 提出一种针对两个约束的可行路径问题的算法，首先将两个约束对应的链路权重加权组合， $d\left(e\right)={\alpha }_1\ast d_1\left(e\right)+{\alpha }_2\ast d_2\left(e\right),\forall e\in E$ ，将两个约束的可行路径问题转化为无约束的最短路问题来求解。Andrew [6] 等人将Jaffee的算法推广到多个约束的路由问题，定义的新权重为 $d\left(e\right)={\displaystyle {\sum }_{i=1}^m{\alpha }_i\ast d_i}\left(e\right),\forall e\in E$ 。随后，在文献 [7] 中，提出TAMCRA (A Tunable Accuracy Multiple Constraints Routing Algorithm)算法，主要考虑以下三个角度，路径的非线性度量、k最短路径方法，非占优路径。在此基础上，文献 [8] 对TAMCRA进行改进，提出了SAMCRA算法。

2.2. 拉格朗日对偶方法

基于拉格朗日的求解算法 [9] [10] [11] ：将CSP问题将时延权重和费用权重进行线性组合，构成一个新的链路权重，线性组合的系数为拉格朗日乘子。该方法不能保证得到的解可以满足时延约束或者满足成本最小。寻找最优的乘子是求解对偶问题的关键，LARAC算法 [9] 是针对CSP问题提出的一种寻找最优乘子的方法：算法采用迭代的方法寻找最短路，每次迭代调整乘子，最终求得对偶最优解，而对于该算法的多项式复杂度的证明没有给出。在此基础上，文献 [10] 中提出了一种新的求解CSP问题拉格朗日对偶问题的方法BiLAD算法，采用截断的方式更新乘子，从而证明了算法是多项式的，并在此基础上给出了精确求解原问题的高效算法。文献 [11] 基于LARAC算法进行推广，设计出可以求解多个约束的最短路问题的拉格朗日对偶问题，但不保证路径的可行性。

本文对CSP问题的拉格朗日对偶问题给出一种全新的求解方法：基于牛顿法的求解算法。原CSP问题 ${\min }_{p}c\left(p\right)={\displaystyle {\sum }_{e\in p}c}\left(e\right),\text{s}\text{.t}.d\left(p\right)\le \Delta$ 的拉格朗日对偶问题为： ${\max }_{\lambda }L\left(\lambda \right)$ ，其中 $L\left(\lambda \right)={\min }_{p}c\left(p\right)+\lambda \ast \left(d\left(p\right)-\text{Δ}\right)$ 。

3. 基于牛顿法的求解算法

3.1. 算法思路

基于牛顿法的思想，为解决CSP问题的拉格朗日对偶问题，本文提出的新的求解算法。其基本思想是：由于CSP问题的特殊性，拉格朗日对偶问题的目标函数 $L\left(\lambda \right)$ 为分段线性凸函数见图1(左)，几乎处处可导，除有限不可微点外，其一阶导函数为如下：

$L^{\prime }\left(\lambda \right)=d\left(\arg {\min }_{p}c\left(p\right)+\lambda \ast \left(d\left(p\right)-\Delta \right)\right)-\Delta$

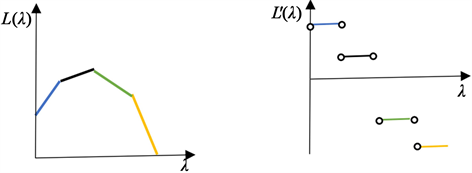
Figure 1. Lagrange dual function and its derivative function

图1. 拉格朗日对偶函数及其导数

由于 $L\left(\lambda \right)$ 的一阶导函数 $L^{\prime }\left(\lambda \right)$ 为分段常值函数见图1(右)，不具备连续性，因此我们利用参数H来近似对偶问题目标函数 $L\left(\lambda \right)$ 的二阶导数，再利用牛顿法更新拉格朗日乘子 $\lambda$ ：

${\lambda }_{n+1}={\lambda }_n-\frac{L^{\prime }\left({\lambda }_n\right)}{H}$

3.2. 拉格朗日乘子的初始上界设置

LARAC算法与BiLAD算法未指定乘子 $\lambda$ 的上届，或初始上届为 $+\infty$ 。我们在几何上考虑CSP问题，并分析费用和时延所构成的二维平面，将端到端的路径所对应的费用以及时延构成的数对作为坐标点，可以将端到端的路径映射到费用–时延平面上。如图2，假设存在5条路径对应图中5个点。通过分析CSP问题的特殊性以及二维平面中的路径位置关系，结合Dijkstra算法求解最短路的方式，本文给出

初始拉格朗日乘子的上届 $\bar{\lambda }=\frac{d\left(p^{-}\right)-\text{Δ}}{c\left(p^{-}\right)-c\left(p^{+}\right)}$ ，其中：

$p^{+}=\arg {\min }_{p}c\left(p\right);p^{-}=\arg {\min }_{p}d(\; p\; )$

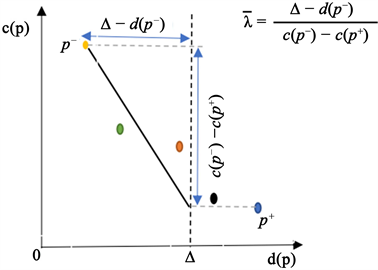
Figure 2. Initial upbound of Lagrange multiplier

图2. 拉格朗日乘子的初始上界

3.3. 算法步骤

Step 0：求解最短路问题： $p^{+}={\min }_{p}c\left(p\right)$ ，判断 $p^{+}$ 是否可行(即： $d\left(p_c\right)\le \text{Δ}$ )，若可行则返回{ $p_c,{\lambda }^{*}=0$ }，否则转Step 1。

Step 1：求解最短路问题： $p^{-}={\min }_{p}d\left(p\right)$ ，判断 $p^{-}$ 是否可行，若不可行则CSP问题不可行，返回{~, ~}，否则转Step 2。

Step 2：计算乘子上下界： $\bar{\lambda }=\frac{d\left(p^{-}\right)-\text{Δ}}{c\left(p^{-}\right)-c\left(p^{+}\right)}$ ， ${\lambda }_0=\underset{\_}{\lambda }=0$ ， $L^{\prime }\left({\lambda }_0\right)=d\left(p_c\right)-\text{Δ}$ 。

Step 3：判断停机条件： $\bar{\lambda }-\underset{\_}{\lambda }<ϵ$ ，若满足，则算法终止，否则转Step 4。

Step 4：计算牛顿迭代点： ${\lambda }_{n+1}={\lambda }_n-\frac{L^{\prime }\left({\lambda }_n\right)}{H}$ ，并计算最短路问题： $p_{n+1}={\min }_{p}c\left(p\right)+{\lambda }_{n+1}\ast d\left(p\right)$ 。若 $p_{n+1}$ 可行，更新 $\bar{\lambda }={\lambda }_{n+1}$ ，否则更新 $\bar{\lambda }={\lambda }_{n+1}$ 。计算 $L^{\prime }\left({\lambda }_{n+1}\right)=d\left(p_{n+1}\right)-\Delta$ ， $n=n+1$ ，转Step 3。

4. 数值实验

本次数值实验部分，我们使用Windows 10操作系统。用C++语言分别编写了BiLAD算法以及本文提出的基于牛顿法的新算法程序。

4.1. 选用的测试数据

本文采用随机生成的网络拓扑来近似真实场景信息传输网络，节点数为{20, 40, ∙∙∙, 500}，每个对应节点数随机生成50个拓扑，计算结果取平均值。此外，为更好地模拟真实通信网络的稀疏性与阶梯时延，节点平均度设置为5，并且将链路时延权重设置为三类：短时延(1 ms~10 ms)、中时延(10 ms~20 ms)、长时延(20 ms~30 ms)，并且链路费用设置与时延成负相关。

4.2. 数值结果

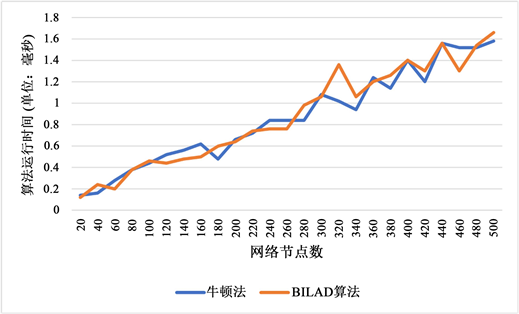
Figure 3. Time consumming comparison between Newton method and BiLAD algorithm

图3. 牛顿法与BiLAD算法运行时间对比

本文比较了CSP的拉格朗日对偶问题求解算法BiLAD算法与本文提出的基于牛顿迭代的新算法的运行时间见图3，从实验结果中可以看出新算法与BiLAD算法相比在网络规模较大的情况下会表现出更高的求解速率，在节点数低于300时，本文新算法与BiLAD算法运行时间相当，说明新算法在求解CSP问题的拉格朗日对偶问题上具有一定优势。

5. 结论

本文针为求解CSP问题的拉格朗日对偶问题，提出一种新的求解算法。一种基于牛顿法的迭代更新格式，我们通过分析CSP问题及其对偶问题的特殊结构，发现对偶问题是分段线性的凸函数，除有限个不可微点外几乎处处可微，且可以通过求解最短路问题来构造出其梯度。对于二阶导数，我们通过利用超参数H进行近似，从而构造出牛顿法的迭代格式。此外，与BiLAD算法不同，本文对于拉格朗日对偶问题的可行域创新性地构造出了更紧的上界。数值实验表明，我们的新算法在算法运行时间等性能上具有一定的优势。