液压S形软管长度计算研究

Research on Length Calculation of Hydraulic S-Type Hose

摘要: 在大型液压系统中，软管作为活动和振动部位的柔性连接件，是管路中不可或缺的一部分。本文结合钻机液压管路装配的实际工程需求，对软管S形弯曲的长度规律进行了理论分析，并根据软管长度规律完成装配。规律表明，在S形管路中，预留的长度处于两种形态的长度范围内时，可以避免软管弯曲小于最小弯曲半径。研究结果有助于想在实际工程中精准计算软管长度范围以防止因为长度误差导致软管寿命降低、增加装配应力等情况。

Abstract: This article proposes a long calculation law for the length of the hose S-shaped shape to solve the calculation of the length of the hose connection between any two oil ports in the case of high pres-sure and large flow in the project. Combining the actual engineering needs of the drilling machine hydraulic tube road assembly, the length range is calculated according to the law of multiple and the hoses at the same time between different oil ports, and the assembly is completed. The assem-bly results show that when the reserved length is within the length range of the two forms in the S-shaped tube road, it can prevent the hose from being bent less than the minimum bending radius while meeting the assembly requirements. The conclusion of the research helps to accurately cal-culate the length of the hydraulic hose in actual engineering to avoid decreased hose life, increased assembly stress, and unable to complete assembly due to the length error.

1. 引言

软管在液压管路系统中被广泛作为活动和振动部位的柔性连接件。与金属硬管不同的是，软管具有一定的柔韧性，适用于在机械结构紧凑的特殊连接处以及相对部位之间使用软管进行连接。在管路系统中布置软管在穿越障碍时笔弯曲、安装硬管简易，同时也会降低成本 [1] 。

在实际工程中，对软管长度进行计算时，通常计算出两端油口的直线距离，然后在直线距离基础上简单增加部分长度后得出总长，以便覆盖软管弯曲时所需的额外长度范围，如长安大学的张奕，刘桦认为软管长度应该增加至总长的102%以作为补偿 [2] 。

简单的增加长度补偿有可能造成许多问题，若软管长度取值过短，则会造成无法装配，或强行装配导致应力过大，降低性能与使用寿命；若软管过长则会导致成本增加，同时在两端油口短距离连接时，软管过长会导致管路弯曲半径减小或扭转，也会造成使用寿命降低 [3] 。

因此，在本文中提出了一种对于软管S形弯曲形状下的长度计算规律，用以解决工程中高压大流量情况下解决任意两油口之间软管连接长度计算。软管的S形弯曲理论包括对软管的基准长度计算以及预留量计算，基准长度即能够满足软管正常连接情况下的最小轴向长度，预留量即软管弯曲的最大适用长度与基准长度间的范围量。通过计算得出软管的基准长度与预留量，可以覆盖软管不同弯曲情况以及制造上的长度偏差，在完成装配的同时避免装配应力和扭转。

2. 液压S形软管长度计算理论

液压管路中，管路将油口与油口建立连通关系，油口通常在液压元件上，常用的油口可分为螺纹型油口、法兰型油口等，管路通过相匹配的接头实现油口之间的连接，管路可由液压软管总成、液压钢管总成或两者的组合构成，其中对于液压软管总成，其两端为刚性扣压接头、中间段为柔性可各向弯曲的软管。通常软管路径可简单切分为S形与L型(图1)，其余复杂管路可以分割转化为这两种基本类型的组合。

本文主要探究S形管路模型的误差范围与长度计算方法，S形管路的长度误差主要来自于液压软管总成长度偏差，以及不同弯曲形态下的长度计算，长度计算主要需要参数为两端油口坐标与软管最小弯曲半径。

2.1. 液压软管长度误差与最小弯曲半径

计算软管的长度原因是因为不同内径与长度下软管有制造偏差和最小弯曲半径要求。不同的制造偏差会造成实际装配中软管的长度与预期长度不同，最小弯曲半径则限制了实际装配中软管的弯曲程度，从而限制软管的长度与转向。

Figure 1. Basic type of hose bending

图1. 软管弯曲基本类型

1) 液压软管长度偏差范围

影响液压软管总成长度的因素在于：制造许可偏差、压力脉动软管胀缩弹性长度变化等。JB/T 8727、GB/T 10544对液压软管总成长度制造许可偏差进行了规范，相关说明如表1所示，可以看出，软管越长、内径越大则许可偏差范围越大，反之越小 [4] 。

Table 1. Manufacturing permissible deviation of hydraulic hose assembly length (Excerpt from JB/T 8727-2017, GB/T 10544)

表1. 液压软管总成长度制造许可偏差(摘自JB/T 8727-2017, GB/T 10544)

液压软管总成长度在制造上满足许可偏差、一定压力下存在胀缩长度变化，两者叠加后其长度具有更多不确定性。油口与油口间的管路连接以软管为主，各类偏差均反映在软管的轴向长度上，软管长度需具备兼容各类偏差的能力。

2) 液压软管最小弯曲半径

液压软管弯曲半径即弯曲部位内侧表面的半径，当弯曲半径达到规定的最小值时称为最小弯曲半径。GB/T 3683、GB/T 10544分别对各类钢丝编织增强层软管、钢丝缠绕增强层软管的增强层外径D、软管外径d进行了较详细的规范，进而对最小爆破压力(最大承压能力值)、最大工作压力、最小弯曲半径等进行了详细限定，基于这些标准生产的软管应对其相关性能进行说明，应用中需根据实际需求进行选定，作为示例，如下表2列出某企R13型四层钢丝缠绕高压软管的相关性能参数 [5] [6] 。

Table 2. Related performance parameters of R13 four-layer wire wound high pressure hose for a company

表2. 某企R13型四层钢丝缠绕高压软管相关性能参数

从上表中可以看出，不同通径规格的高压软管最小弯曲半径与外径的比值在7.5~8.9区间。

2.2. 液压软管基准长度及预留量计算

为计算油口的准确长度，需要建立空间坐标，空间坐标符合笛卡尔左手定则，如图2所示，左手拇指指向Y轴正向、食指指向Z轴正向，中指指向X轴正向。三个坐标轴相互垂直，含负方向在内三个坐标轴共指向六个方向。

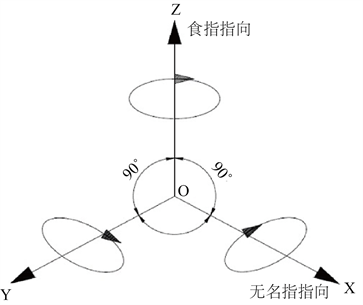
Figure 2. Cartesian left-hand rule spatial coordinates

图2. 笛卡尔左手定则空间坐标

液压元件可能分布在空间任意位置，为便于坐标定位及数值统一，首先应设定一个全局基准坐标，用符号(x₀, y₀, z₀)表示，全局基准坐标的空间坐标值为(x₀, y₀, z₀) = (0, 0, 0)。全局基准坐标作为空间的尺寸零点，仅有一个，在选取时应放置在几何中心或容易作为基点对其他元件进行定位。

液压元件上有连接管路的油口，油口坐标根据其对应的子坐标取值，此时将子坐标作为原点基准，油口坐标应以其管路连接的中心为位置点，油口坐标设定为符号(x_ni, y_ni, z_ni)，其中 $i=1,2,3,\cdots$ 为油口数量，n为前述子坐标数量。

基于空间坐标对管路路径合理性进行配置后，需要对软管长度在理论上进行确定。软管的理论长度不考虑各类尺寸偏差，是理论上的准确值，将其称为软管的基准长度。用于计算软管基准长度的路径形式常用的为S形、L弯曲形等，其他计算形式的路径可由这两种形式转换得到。

建立如图3所示的空间模型，设定有两个油口O₁₁ (x₁₁, y₁₁, z₁₁)、O₂₁ (x₂₁, y₂₁, z₂₁)，将S形管路油口看作是一个空间立方体的对角线两端点，考虑接头尺寸后的坐标作为软管路径的起始/终止点并按对角点绘制，则S形路径所在的平面为ABMN，其中L为路径棱边AB的长度，H为棱边BC和CM组成的三角形斜边BM长度，即：

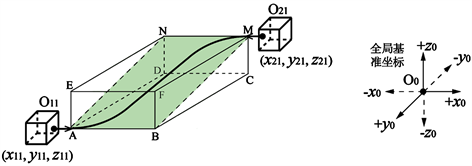
Figure 3. S-shaped hose path space model

图3. S形软管路径空间模型

$L=\left|AB\right|=y_{21}-y_{11}$ (1.1)

$H=\sqrt{{\left|BC\right|}^2+{\left|CM\right|}^2}=\sqrt{{\left(x_{21}-x_{11}\right)}^2+{\left(z_{21}-z_{11}\right)}^2}$ (1.2)

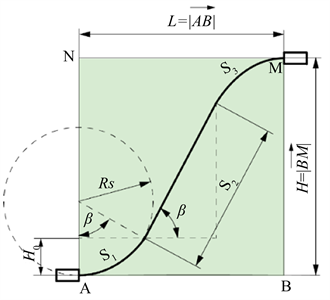
易知ABMN为一个长方形平面，S形路径位于其上，S形路径转换为ABMN平面上的模型如图4所示，R_S为软管中心线弯曲半径，β为弯曲段弧度角且 $0\le \beta \le \pi /2$ 。

(a) (b) (c) (d)

Figure 4. Geometry of S-shaped hose path planning

图4. S形软管路径规划几何图

S形路径总长度为：

$S=S_1+S_2+S_3$ (1.3)

由几何关系，可得：

$S_1=S_3=R_S\cdot \beta$ (1.4)

$S_2=\frac{H-2H_0}{\sin \beta }$ (1.5)

其中 $H_0=R_S\left(1-\cos \beta \right)$ ，联立式(2.37)~(2.39)可得

$S=2R_S\cdot \beta +\frac{H-2R_S\left(1-\cos \beta \right)}{\sin \beta },0\le \beta \le \frac{\pi }{2}$ (1.6)

另外，根据几何关系还可得到

$L=2R_S\sin \beta +S_2\cos \beta =2R_S\sin \beta +\frac{H-2R_S\left(1-\cos \beta \right)}{\sin \beta }\cdot \cos \beta$ (1.7)

令 $\sin \beta =m$ ，且 $0\le m\le \text{1}$ ，则 $\cos \beta =\sqrt{1-m^2}$ ，式(2.41)可变换为

$L=2R_S\cdot m+\frac{H-2R_S\left(1-\sqrt{1-m^2}\right)}{m}\cdot \sqrt{1-m^2}$ (1.8)

不难看出，R_S取最小弯曲半径时，S形路径长度最小，设定为S_min，如图4(a)所示路径；软管路径最大长度则需要根据H，L长度情况进行划分：若H > 2R_s时，如图4(b)所示路径， $R_S=0.5L=0.5\left|AB\right|$ 时S形路径长度最大；若H < 2R_s且L/H < tanβ时，如图4(c)所示，取R_s为最小弯曲半径，路径长度为两个圆弧弧长之和时，路径长度最大；若H < 2R_s且L/H > tanβ时，如图4(d)所示，取R_s为最小弯曲半径，路径长度为两个圆弧弧长以及剩余直线端之和时，路径长度最大，为S_max。若软管路径长度应在S_min~S_max之间取值，取较大值时软管长度有较大的预留量、对尺寸偏差兼容性好，取较小值时预留量就小、对尺寸偏差兼容性差，预留量应在合理范围内。作为不考虑偏差的理论值，选用S_min作为基准长度，即

$S=S_{\min }=2r_{\min }\cdot \beta +\frac{H-2r_{\min }\left(1-\cos \beta \right)}{\sin \beta },0\le \beta \le \frac{\pi }{2}$ (1.9)

其中：r_min为软管最小弯曲半径；H为图4中线段长度；β为图4中弧度角。

2.3. 液压软管长度及其预留量

液压软管长度预留量即是用来兼容管路中的各类尺寸偏差。

从图5可以看出，若无尺寸偏差，软管长度取为基准长度l便可将其对应的液压软管总成进行装配，且没有多余的长度尺寸；考虑尺寸偏差后，软管长度为l₀，两者之间的差值即为液压软管长度预留量，设定为符号 $\delta$ ，可表达为

$\delta =l_0-l$ (1.10)

软管长度预留量用于抵消尺寸偏差，偏差可能为正、也可能为负，为同时兼顾各类因素，采用中间值的方式推荐给定软管长度预留量，其表达式为

$\delta =0.5{\delta }_{\max }=\frac{S_{\max }+S_{\min }}{2}$ (1.11)

其中： ${\delta }_{\max }$ 为由式(1.11)得到的软管长度最大预留量。

Figure 5. Length of hydraulic hose

图5. 液压软管长度

通过式(1.9)计算，得出在软管以最小弯曲半径与直线段结合所规划出最小长度路径S_min和保持软管在最大弯曲幅度下的最大长度路径S_max。在任意两个油口之间都能够得出长度范围，并覆盖安装误差、装配误差以及制造误差等情况。

3. S形管路理论实际应用

3.1. 背景概述

旋挖钻机的液压系统中一部分元件如下图所示，需要在M7阀与多通块之间进行连接，多通块四个入口连接上水平、竖直方向上的M7阀出油口。连接的软管总称型号为V87612-FS20-20/V87612- FS20-20/1100，两端连接油口为SAE 11/4重型法兰油口，M7阀与多通块的垂直距离为1063 mm，连接油口如下图6所示：

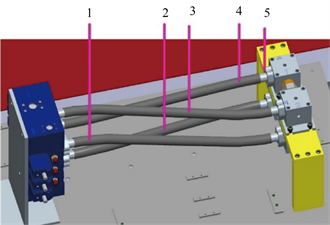
Figure 6. Oil port model at both ends of rotary drilling rig

图6. 旋挖钻机两端油口模型

四对连接油口分别为：A3连接油口3，A2连接油口4，B3连接油口1，B2连接油口2。

3.2. 软管长度和预留量计算

以A3连接油口3为例，进行长度计算。

首先以A3和油口3为两端为O₁₁和O₁₂建立空间坐标系，设定直线坐标，如下图7所示：

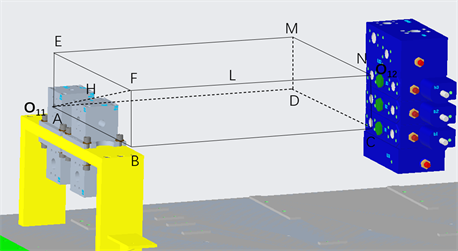
Figure 7. Oral space coordinate system at both ends

图7. 两端油口空间坐标系

其中H为AF长度，L为FN长度，计算拉直总长度L_s，长度由接头长度a₁，a₂与软管长度l决定：

$L_s=a_1+l+a_2$ (2.1)

$l=\sqrt{H^2+L^2}$ (2.2)

其中两边接头均为SAE 11/4重型法兰接头，因此a₁与a₂均为58.8 mm；H和L为已知量，分别为924.7 mm与230.24 mm，计算可得油口直线长度L_s为1070.53 mm，软管的直线距离l为952.93 mm。

中间S形路径胶管基准长度S根据式1.3计算。根据表2可知软管最小弯曲半径R_s为405 mm，根据式1.8可以算出β的值为0.273，即在最小情况下，β角度为15.642˚，根据式1.9计算得出软管部分基准长度S_min为963.81 mm。

由于H < 2R_s，且L/H < tanβ，因此选择软管最大长度S_max计算公式为：

$S_{\max }=S_1+S_2+S_3=2R_s\cdot \beta +l$ (2.3)

其中软管弯曲角度β和直线段长度l根据下式求出：

$H=2R_s\cdot \left(1-\cos \beta \right)$ (2.4)

$L=2R_s\cdot \sin \beta +l$ (2.5)

可以得出，β的值0.773，即为44.31˚，直线段l为358.87 mm，根据式2.3可计算得出S_max为985.00 mm。

根据软管基准长度S_min为963.81 mm，最大总长度S_max为985.00 mm，则软管预留量为

${\delta }_{\max }=S_{\max }-S_{\min }=21.19\text{mm}$ (2.6)

根据式1.11可得选取预留量 $\delta$ 为总预留量一半，则最终选取软管长度为：

$S=S_{\min }+\delta =974.41\text{mm}$ (2.7)

其余三根软管计算方法同上，得出软管总长度分别为978.46 mm，961.23 mm，936.94 mm，根据求出软管长度与弯曲半径，在三维图中装配情况如下图8所示：

Figure 8. Three-dimensional assembly model

图8. 三维装配模型

实际安装效果如下图9所示：

Figure 9. Pipeline system engineering application example of rotary drilling rig

图9. 旋挖钻机管路系统工程应用实例

可以看出经过计算得出总长度的四根软管，经过安装之后能够在避免过度弯曲在最小弯曲半径内的情况下，精准的连接在M7阀和液压多通块之间，既防止了软管长度过小导致的安装困难甚至无法连接，也避免了软管长度过大导致过分弯曲扭转造成的软管承压能力和使用寿命下降。并且在进行实际装配之前，根据理论得出的长度、弯曲半径与设计路径，在三维模型中进行模拟装配，验证各软管之间没有干涉后，再进行实际应用，装配效果较好。

4. 结语

针对S形液压软管的长度计算问题，本文基于空间坐标系的管路路径计算方法，将软管的长度计算转换为在一个空间立方体对角线两端的连接长度计算。首先根据软管总成型号确认最小弯曲半径，并根据油口两端直线距离估算软管总称长度偏差。然后基于空间坐标，由管路路径规划后获得不考虑偏差影响下的软管基准长度。在考虑偏差后软管需要有合理的预留量，提出一种最小限度弯曲的软管长度预留量计算方法，在最小弯曲半径限度内计算软广长度预留量的最大值，为同时兼顾偏差可为正、可为负的可能性，取最大预留量的一半即中间值作为软管长度的预留量，基准长度与预留量之和即为软管的长度，再考虑软管扣压接头长度即得到液压软管总成的长度。最后，通过旋挖钻机动力头管路路径规划实例，对其S形管路路径长度进行了计算，获得有充足预留量的软管长度。

本文提出的S形软管长度计算理论，可以计算得出实际工程中任意两油口之间的软管长度最大值最小值间范围。在实际工程中，在设计阶段通过S形软管长度计算理论进行长度计算，同时配合三维建模模拟装配，可以为国内软管长度设计、装配提供一种更精确、便捷的解决方法。