不同直径和流量对层叠式微通道散热器热性能的影响研究

Effects of Diameters and Flow Rates on Thermal Performance of Multi-Layered Microchannel Heat Sink

摘要: 本文基于PCHE板提出层叠式微通道散热器，并对其在不同直径和流量下进行了数值模拟分析。结论表明，增大流量可以增强散热器换热性能，当散热器一个分析单元的流量从20 ml/min增至40 ml/min时，热阻可降低约35%，但随着流量的进一步升高热阻的减小率也会逐渐下降。流量保持一定时减小通道直径也可以达到增强换热的效果，但增大流量以及减小通道直径都会引起压降的增加。层叠式微通道散热器各层通道的换热情况不相同，底层流体在入口处附近换热较强，而高层部分的流体在入口处换热很弱。在充分发展段，各层通道流体与壁面换热的Nu数趋于一致。

Abstract: In this work, a multi-layered microchannel heat sink is proposed based on PCHEs, and the numerical simulation analysis is carried out under different diameters and volume flow rates. Increasing the flow rate can enhance the heat transfer performance of the heat sink. When the flow rate increases from 20 ml/min to 40 ml/min, the thermal resistance can be reduced by 35%, but as the flow rate further increases, the reduction rate of thermal resistance will gradually decrease. And when the volume flow rate remains constant, reducing the channel diameter can also achieve the effect of enhancing heat transfer, but both increasing the flow rate and reducing the channel diameter will increase the pressure drop. The heat transfer conditions of each layer of the multi-layered microchannel heat sink are different. The heat transfer of the bottom fluid is strong near the inlet, while the heat transfer of the fluid in the upper layer is weak at the inlet. In the fully developed region, the Nusselt number of the heat transfer between the fluid and the channel wall in each layer tends to be consistent.

1. 引言

随着电子技术的不断革新，电力电子器件及其装置系统也朝着高度集成化的方向发展。结构紧凑且性能优越的电子设备不仅可以大幅提升运行效率，同时还可降低系统对于空间的占有率，但这也会带来在高功率密度下，系统可靠性低、寿命缩短等问题。这类问题大多是由于温度分布不均，致使局部温度过高而超过允许最高温度，或是在热应力作用下发生变形引起。有文献表明，电力电子设备超过50%的故障是由于温度过高引起 [1] 。普渡大学CTRC研究中心大胆预测，未来全数字雷达T/R组件的热流密度将可能超过500 W/cm² [2] ，在特殊领域的高功率系统，如国防电子中的高功率防御雷达、微波武器等，电力电子行业的大功率IGBT (Insulated Gate Bipolar Transistor，绝缘栅双极晶体管)模块其功率密度可达10²~10³ W/cm²量级 [3] [4] [5] 。因此，为确保电子器件能够安全稳定地运行，亟需要发展高效可靠的散热技术。在现阶段的电子器件领域，散热技术已经成为了整个系统的核心技术之一，同时也是制约电子设备进一步发展的技术瓶颈，成为了近些年来的研究热点。

1981年，Tuckerman和Pease [6] 首次提出具有微小通道的紧凑型散热器，充分利用了通道内层流换热的对流换热系数与通道水力直径成反比的特点，将通道截面尺寸减小到微米量级，既能显著增强换热，还能减低散热器的重量和尺寸。从此，微通道散热器便引起了广泛学者的研究，为进一步拓展微通道散热器性能，Vafai和Zhu [7] 提出具有双层通道的微通道散热器，进而由Wei等 [8] 扩展为多层式。常见的微通道散热器为矩形截面通道，截面纵横比较高的矩形通道可以尽可能提供更大的散热面积，但相比之下其压降也很大 [9] 。且散热器的制造方式多为表面刻蚀、挤压和铸造等，从制作工艺上来看高纵横比的通道难以加工 [10] [11] 。另一方面，PCHE (Printed Circuit Heat Exchanger, PCHE)加工技术成熟，作为高度紧凑的热交换器，已经在各个工业领域得到了应用 [12] 。因此，将成本低廉、性能优越的PCHE推广于电力电子设备的散热成为可能。本文基于成熟的PCHE制造技术，提出层叠式微通道散热器，利用数值模拟方法考虑其在高热流、大尺寸散热场景下的热性能。

2. 层叠式微通道散热物理数学模型

2.1. 物理模型

本文所研究的层叠式微通道散热器几何示意图如图1所示，通道截面为刻蚀工艺下典型的半圆形状。冷却水从入口各通道均匀流入，与通道内表面换热后经出口流出，达到散热的效果。底部是厚度为t的基板，其底部为受热面，尺寸为W × L = 50 mm × 100 mm，热流密度为q = 200 W/cm²；散热器为厚度为b的PCHE板经扩散键合的方式拼接而成，半圆通道的直径记为d，考虑到实际传热过程中沿散热器高度H方向存在温度梯度，为降低该温度梯度形成的热应力对各PCHE板连接面上的影响，因而选择将PCHE板在散热器宽度W方向上进行拼接。从热阻的角度来看，基板厚度越小其热阻也越低，本文将基板设置为固定厚度1 mm。由于散热器由多块PCHE板拼接而成，在宽度方向上具备周期性的特点，因此在分析的过程中可以选取其中的一个单元以简化计算，如图1中虚线所示。

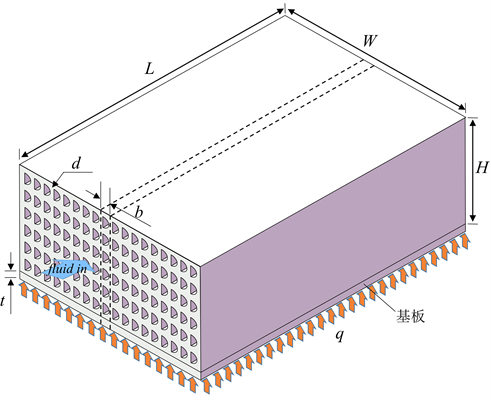
Figure 1. Schematic diagram of the multi-layered microchannel heat sink

图1. 层叠式微通道散热器结构示意图

2.2. 数学模型及边界条件

对于通道内的流体流动，层叠式微通道散热器因其巨大的换热面积使得其可以在小流量条件下应对较高的热负荷，因而通道内流动通常处于层流状态，为进一步简化问题，可结合实际做出如下假设：

1) 通道内的流动为稳定的不可压缩层流流动；

2) 流体介质为牛顿流体，且为单相流动；

3) 流体与固体的物性参数为常数；

4) 忽略重力、辐射等因素的影响；

5) 忽略因流体粘性作用由机械能转化成的热能。

根据以上假设，关于流体域质量、动量和能量的控制方程可简化为如下张量形式：

质量方程：

$\frac{\partial u_{\text{i}}}{\partial x_{\text{i}}}=0$ (1)

动量方程：

$\frac{\partial u_{\text{i}}{u}_{\text{j}}}{\partial x_{\text{j}}}=-\frac{1}{{\rho }_{\text{f}}}\frac{\partial p}{\partial x_{\text{j}}}+\frac{{\mu }_{\text{f}}}{{\rho }_{\text{f}}}\frac{{\partial }^2{u}_{\text{i}}}{\partial x_{\text{j}}\partial x_{\text{j}}}$ (2)

能量方程：

$\frac{\partial T{u}_{\text{j}}}{\partial x_{\text{j}}}=\frac{{\lambda }_{\text{f}}}{{\rho }_{\text{f}}{c}_{\text{pf}}}\frac{{\partial }^{2}T}{\partial x_{\text{j}}\partial x_{\text{j}}}$ (3)

式中ρ_f为流体的密度，kg/m³；μ_f为流体动力粘度，kg/(m·s)；λ_f为流体导热系数，W/(m∙K)；c_pf为流体比热容，J/(kg∙K)。对于固体区域，内部只存在导热过程，只需将能量方程式(3)中速度取为0，物性参数取为固体的即可。对于传热单元数值模拟的边界条件设置如图2所示：

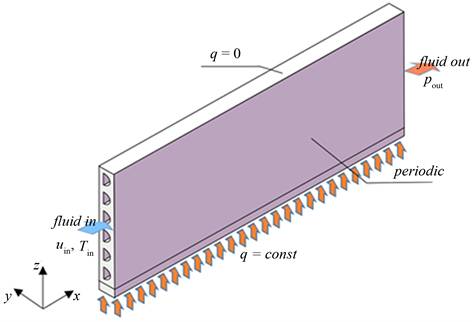
Figure 2. Schematic diagram of numerical simulation cell

图2. 数值模拟单元简图

各个工况下进入通道的流体速度和温度保持稳定，出口设置为压力出口：

$x=0,T=T_{\text{in}}=293.15\text{K},u=u_{\text{in}};x=L,p=p_{\text{out}}$ (4)

所有的流固交界面为热耦合壁面，且速度无滑移：

${-\lambda \frac{\partial T}{\partial n}|}_{\text{s}}={-\lambda \frac{\partial T}{\partial n}|}_{\text{f}},{T|}_{\text{s}}={T|}_{\text{f}},u=v=w=0$ (5)

顶部为绝热边界：

${\frac{\partial T}{\partial z}|}_{z=t+H}=0$ (6)

底部为恒热流边界：

${-\lambda \frac{\partial T}{\partial z}|}_{z=0}=q=200{\text{W/cm}}^2$ (7)

单元两侧为周期性导热边界：

$T\left(y=0\right)=T\left(y=b\right),{-\lambda \frac{\partial T}{\partial y}|}_{y=0}={-\lambda \frac{\partial T}{\partial y}|}_{y=b}$ (8)

对于散热器和冷却剂材料的选择，目前常用的散热器材料为铝、铜等，其他如银、金、金刚石也都是良好的导热材料，但因其高昂额成本则少被采用。本文选用导热性能更高的铜作为散热器材料，选用水作为冷却介质，铜和水的热物性参数如表1所示。

Table 1. Thermal properties of copper and water

表1. 铜和水的热物性参数

2.3. 散热器热性能评价参数

本文取散热器最大温差下对应的单位面积热阻作为热性能评价参数，其具体表达式定义为：

$R^{″}=\frac{T_{\max }-T_{\text{in}}}{q}$ (9)

其中T_max表示受热面最高温度，T_in则表示散热器最低温度，也即冷却介质的入口温度。

另一个性能参数为散热器通道流体的压降，其表达式为：

$\Delta p=f\frac{L}{D_{\text{h}}}\frac{1}{2}{\rho }_{\text{f}}{u}_{\text{m}}^2=\frac{Po}{Re}\frac{L}{D_{\text{h}}}\frac{1}{2}{\rho }_{\text{f}}{u}_{\text{m}}^2$ (10)

其中Re为雷诺数，Po为泊肃叶数，D_h为水力直径，半圆截面的水力直径为：

$D_{\text{h}}=\frac{\text{π}}{\text{π}+2}d$ (11)

2.4. 网格无关性及模型验证

由于数值模拟单元在长度方向和截面方向上尺度相差两个数量级，需要选用合适的网格尺寸以控制网格数量并保证计算精度。选用GAMBIT软件通过扫掠面网格的方式进行体网格划分，长度方向的网格精密程度会影响压力场的计算精度，选用压力为监控量做网格无关性检验。如图3所示，随着网格数量的增多，通道的压降趋于平缓，最终选取第三套网格的划分方法。即沿流动方向布置600个网格节点，端面上对于固体域与流体域各自采用尺寸约0.02 mm和0.01 mm大小的面网格。

模型的准确性验证是数值模拟工作的重要环节，由于缺乏半圆截面的层叠式微通道散热器的相关文献，本文选用文献 [13] 中优化后的双层式矩形截面微通道进行模型验证，在与文献相同工况下对散热器取一个分析单元进行数值模拟，对比散热器总热阻。如表2所示，对于双层式矩形微通道，散热器总热阻验证值与文献值偏差为3.6%。偏差在工程可接受范围内，由此可确保本文数值模拟的准确性。

Table 2. Verification of double-layer rectangular channel

表2. 双层矩形通道模型验证

Figure 3. Grid independence test

图3. 网格无关性测试

3. 数值模拟分析

层叠式微通道散热器的传热性能不仅与流体的工作参数有关，还与散热器的几何尺寸相关。本文对具有8层通道的微通道散热器进行数值模拟，探究通道在不同直径d、以及流量Q_V下的散热器的性能。将分析单元的宽度控制为0.4 mm，单元的总体积流量取为20 ml/min，40 ml/min，60 ml/min，80 ml/min，100 ml/min，通道直径d从0.2 mm到0.5 mm变化。

图4展示了散热器单位面积的热阻随流量和通道直径的变化关系。在直径大小一定时，散热器内的导热热阻不发生变化，随着通道流量的增加，流体与壁面之间的换热强度得到提升，大流量的流体也可以吸收更多的热量，对应的流体沿流动方向因吸热带来的温升热阻可以有效降低，从而使散热器热阻有效地呈现下降趋势。以直径为0.2mm的通道为例，流量从20 ml/min增大至40 ml/min，相应的热阻值由0.4 K/(W/cm²) 减小至0.26K/(W/cm²)，减小了约35%。但随着通道流量的进一步增大，强化换热的效果也在逐步减弱，因为在大流量下流体与散热器换热的过程已经得到了足够的强化，对于传热过程的强化应该着重于改善传热热阻更大的环节。同样，对于固定的流量，如果通道的直径减小，通道表面的对流换热系数成反比例增大，进而达到增强换热的目的。但是，在散热器层数和高度固定时减小微通道直径意味着将会有更多的固体作为导热介质，也即通道之间的固体导热热阻也会随之增加。因此，从图4中可以看到，通道直径减小所带来的热阻降低的效应也在逐步变弱，在流量较小的时候，相比于改变通道尺寸，增大流量是更为有效且更加便捷的方法。

值得注意的是，增强传热往往以更多的泵功或则更大的压降为代价，将雷诺数Re以及水力直径Dh的定义式带入式(10)，可得出压降关于流量和直径的显式表达式：

$\Delta p=\frac{4Po}{\text{π}}{\left(\frac{\text{π}+2}{\text{π}}\right)}^2{\mu }_{\text{f}}L\frac{Q_{\text{V0}}}{d^4}$ (12)

其中Q_V0指单个通道的体积流量。图5展示了在不同流量和直径下，散热器压降的变化情况，由于压降与流速正相关，在流量增大时，压降也会呈线性方式增加，而在流量一定的条件下减小通道直径时，压降的增幅则更快，因为它与直径的4次方呈显式的反比关系。

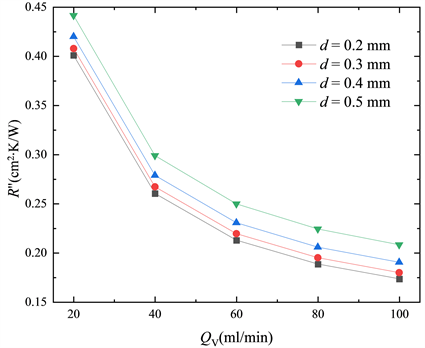
Figure 4. Variation of thermal resistance with volume flow

图4. 热阻随流量的变化

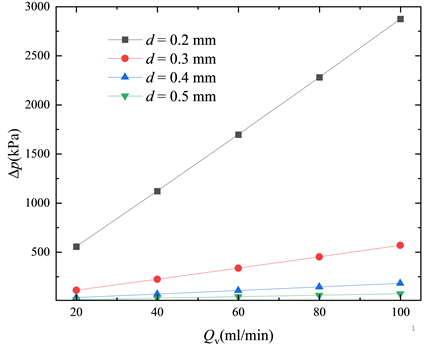
Figure 5. Variation of pressure drop with volume flow

图5. 压降随流量的变化

对于通道内部的传热，热量从散热器底部输入，经下层通道的流体吸热后传导至上层通道。对于所分析的散热单元，由于肋片效应使得每一层通道的换热强度也有所不同，且对于通道内流体来说无法直接断定通道壁面是什么样的热边界条件。将各层通道沿流向划分为20小段，取每一段壁面上平均热流密度代表该段的局部热流密度，可做出壁面热流沿流动方向的变化曲线。如图6中显示了在直径为0.2 mm，散热单元总流量为20 ml/min时，各层通道表面的热流密度沿流动方向的分布情况。对于底层通道的入口部分，由于离热源面最近，因此流体可以吸收大量的热量，表现出较高的热流密度，在最底层通道入口处热流密度可超过300,000 W/m²，而随着流动过程中不断地吸热升温，其吸收热量的能力也逐渐下降，换热强度有所降低，也即热流密度的大小逐渐减小。而对于上层通道却恰恰相反，由于入口处附近从加热面输入的热量已经被底层流体充分吸收，使得传递至上层通道入口处的热量很少，即热流密度在入口附近的值较低。图6中还能看到上层部分的通道表面热流密度沿流动方向逐渐增加，这是因为底层流体沿流动方向吸热能力降低，因此热量得以传递至上层通道。同样地，针对每一小段提取热流和换热温差可得出对流换热系数变化情况，图7显示了通道表面局部换热系数沿流动方向的变化。可以看到，由于入口段效应，各通道内换热系数整体在入口附近相对更高，但每一层通道表面的换热系数有所区别，尤其是在入口附近，层数越高的通道对应的局部换热系数也越大，这主要是因为各层流体的热边界不同的影响。底层通道虽然具备更高的热流密度，但相应的壁面与流体温差也更高，上层部分相比于下层部分的通道在入口附近的热流密度更低，但同样的流量下低换热量使得壁面和流体的温差也更小，因此造成其换热系数相对更高。各层通道流体换热系数在充分发展阶段趋于一个定值，约为20,000 W/(m²∙K)，此时以水力直径作为特征尺寸可折算出努塞尔数Nu约为4.03。

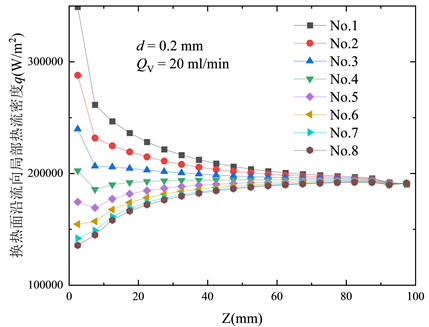
Figure 6. Distribution of channel surface heat flux along flow direction

图6. 通道表面热流密度沿流向分布情况

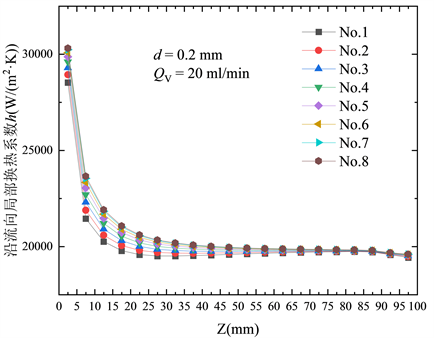
Figure 7. Distribution of convective heat transfer coefficient along flow direction

图7. 通道表面对流换热系数沿流向分布情况

4. 结论

本文基于成熟的PCHE制造技术提出适用于电力电子设备的层叠式微通道散热器。并对具有不同直径和流量的散热器单元进行了数值模拟分析。结论得出，增大流量和减小直径均可增强散热器热性能，但随着流量的持续增大，热阻减小的趋势也趋于平缓，而减小直径所带来的强化换热效果相比之下并不明显，且小直径大流量的情况下会导致压降激增。在实际情况中，应兼顾热阻和压降选择合适尺寸的散热器。结合模拟结果，以散热单元流量为20 ml/min，直径为0.2 mm时的工况为例详细讨论了层叠式微通道散热器内的换热过程。散热器上下部分的通道换热方式有所区别，主要是因为底层流体在入口处率先吸收入口附近的热量，而从散热器后程部分输入的热量则通过底层流体传递至上层流体。各层通道流体换热系数在充分发展阶段趋于一个定值，此时折算的努塞尔数Nu约为4.03。