多重边复杂网络牵制同步控制节点集优化

Optimal Pinning Control Synchronization of Node Groups for Multi-Edges Complex Networks

摘要: 针对多重边复杂网络的牵制同步控制节点选取问题，提出一种基于图论的优化牵制节点组选择的策略。根据网络中边的性质不同，基于网络拆分的思想，通过引入时延将网络进行拆分。根据李雅普诺夫稳定性理论，使用自适应牵制控制器以及图论和矩阵分析等知识，得到可以优化多重边复杂网络牵制节点组选择的方案：当牵制节点个数固定时，从网络的对称拉普拉斯矩阵中删除受控节点所对应行和列后所得子矩阵的最大特征值，用此来衡量牵制方案的有效性。即：网络中单个节点的动力学系统与耦合强度给定时，最大特征值越大，牵制方案越有效。与此同时，对最大特征值的谱特性进行分析，以此对优化牵制方案提供理论支持。

Abstract: Aiming at pinning synchronization control node’s selection in multi-edges complex networks, a strategy based on graph theory to optimize the selection of pinning node groups is proposed. According to the edges’ properties that is different in the network, based on the network splitting’s idea, the network is split by introducing delay. According to Lyapunov stability theory, using adaptive pinning controller, graph theory and matrix analysis’s knowledge, a scheme that can optimize pinning node groups’ selection in multi-edges complex networks is obtained: When the pinning nodes’ number is fixed, the maximum eigenvalue of the sub matrix obtained by deleting the rows and columns corresponding to the controlled nodes from the symmetric Laplacian matrix of the network is used to measure the pinning scheme’s effectiveness. That is, when the dynamic system and nodes’ coupling strength in the network are given, the larger the maximum eigenvalue, the better the effectiveness of the pinning scheme. At the same time, the spectral characteristics of the maximum eigenvalue are analyzed, which provides a theoretical support for the optimization of the pinning scheme.

1. 引言

随着研究人员对各个领域研究的不断深入，其中对于复杂网络的研究已经成为人们关注的热点话题。复杂网络是根据网络中的连接拓扑结构将众多节点相互连接，从而表现其动力行为的一门新兴的交叉学科。自复杂网络产生开始，学者们就将目光投射到了它的身上，并且沿着图论继续发展从而成为了一门交叉学科，因此可以将图论作为复杂网络发展的源头。自1736年“哥尼斯堡七桥问题”被Euler研究后，在数学方面一个全新的领域被图论和几何拓扑所打开，但是在研究复杂网络方面图论虽然是一个非常实用的数学工具，但是它却局限于规则网络模型；直到1960年随机图理论被数学家Erdős和Rényi [1] 建立，这是一个可以通过概率来衡量两个节点之间是否存在连接关系的新方法，为人们研究随机网络提供了理论基础；在接下来的几十年里，随着社会科学发展和研究者们的不断深入，小世界网络模型在1998年时被Watts和Strogatz [2] 提出，并对网络的小世界效应进行了分析；随后在1999年Barabási和Albert [3] 又提出了网络连接具有幂律分布规律的无标度网络模型 [4] ，新研究的这些成果无疑为复杂网络的发展提供了强大的推动力，为研究者们之后的探索提供了坚实的基础，使得复杂网络理论开始迅猛发展。

由于复杂网络在现实生活中被不断应用，那么控制复杂网络便成为了研究复杂网络的终极目标，所以使复杂网络同步逐渐提升为网络科学中的热门话题。同步 [5] 是一种集体行为，在现实生活中是一类备受关注的非线性现象，它展现了复杂系统之间一种互相合作的关系，即起始状态不同的系统可以在经过一段时间的调整后最终呈现出相同模式的状态。现如今，在很多通信系统、激光系统等领域，同步已经占领着非常重要的地位。对此，很多同步控制方法随之产生 [6] ：自适应控制 [7] 、牵制控制 [8] 、线性反馈控制 [9] 、脉冲控制 [10] 等。

在实际网络中，一方面大多数策略侧重于设计方法和实现手段，而牵制控制着重于对网络的结构进行研究；另一方面随着复杂网络结构的复杂性不断提高，如果对网络中的所有节点全部施加控制，这无疑是一个既浪费成本又浪费人力资源的一种手段，所以如果通过恰当的使用牵制方法，以此加入控制器给网络中的一部分点，使得全部节点之间相互作用，从而对网络整体进行控制。牵制控制首次被Chen [11] 提出，并且使无标度网络达到了同步状态。Chen [12] 发现当牵制控制增益足够大时，复杂网络可以通过一个控制器就可使整个系统达到同步。Zhou [13] 等人提出了在一般的复杂网络中，牵制自适应同步的一些局部和全局的准则。Chen [14] 通过使用自适应技术，在找到合适的耦合强度下实现了复杂网络的同步，并且发现在任何的线性牵制方案下，复杂网络都可以通过自适应调整耦合强度来实现同步。

以往在研究复杂网络同步时，我们主要针对的是节点的选择，对此学者们已经做了大量的研究。其中针对复杂网络的牵制控制策略有很多的研究成果：随机牵制控制策略 [15] 、基于度的牵制控制策略 [16] [17] 、基于中介数(BC)的牵制策略 [18] 等。Rong和Li [18] 提出了基于中介数的牵制策略，决定优先选择介数中心度较大的节点进行牵制；文献 [19] 通过利用K-shell分解法对复杂网络中心位置的节点进行查找，发现牵制k-core数大的节点可以使复杂网络同步的效果更好；一种基于数据流的牵制控制策略被Wang和Liu [20] 提出，它使复杂网络达到同步的效果与基于中介数的牵制方案很接近，但是可以使计算量减少。以上众多成果都是对于单个节点选择进行不断优化，但是当牵制节点个数给定时，如何选择一组合适的节点组来优化牵制效果却没有过多的研究。对此，在本文我们将对多重边的网络进行研究，因为在以往大多数文章中多偏向于对单边复杂网络进行研究，但是在现实生活中，如：交通网、人际网、通信网等都是由多种性质的子网络构成的多重边融合复杂网络 [21] ，这种网络相对于单边复杂网络而言有更加复杂的拓扑结构、节点动力学特征，所以对于两个节点之间的多重边不能进行简单的合并，需要找到稳妥的方式对其进行划分。不仅如此，我们还引入了时延，因为在真实的网络中，由于信号在传播的过程中的速度是有限的、节点和节点之间的物理距离有些时候也会变得很远、有些时候也会受到网络宽带速度等限制等多种原因，会导致在自然界和社会的很多真实的网络中出现时延 [22] [23] ，因此时延在日常生活中是一种普遍存在的客观现象。在此我们以交通网为例：一个交通网是由很多种不同的交通运输工具所构成的大型网络，如：航空网、地铁网、公交网等等，为了便于管理，研究者们将这种含有多种交通方式的网络进行划分，将具有相同运输方式的网络，即传输速度相同的作为一个子网，传输速度最快的网络被称为“零子网”，其他网络的传输速度相比它总是慢的，所以在传输过程中产生时延，即其他网络传输速度都是低于零子网的。基于上述原因，笔者基于边之间传输速度的不同对复杂网络进行划分，建立了多重边的复杂网络模型，并对其优化牵制效果的节点组选择方案进行了系统深入的研究。

本文其他章节的安排如下：第二部分讲解了多重边复杂网络模型，并且对全文所能应用到的假设和引理进行梳理；第三部分对多重边复杂网络牵制同步控制进行研究，得到了在自适应牵制控制器作用下复杂网络全局同步的准则，并且对对称子拉普拉斯矩阵的最大特征值的谱特性展开研究；第四部分进行了数值仿真，对所得到的理论成果进行验证。

2. 模型准备及描述

本考虑由N个节点构成的连续时间线性耦合动态网络模型：

$\stackrel{\dot{}}{x}\left(t\right)=f\left(x_i\left(t\right)\right)-c{\displaystyle \underset{j=1}{\overset{N}{\sum }}{P}_{ij}}H{x}_j\left(i=1,2,\cdots ,N\right)$ (1)

其中 $x_i\left(t\right)={\left(x_{i1}\left(t\right),x_{i2}\left(t\right),\cdots ,x_{in}\left(t\right)\right)}^{\text{T}}\in R^n$ 是节点i在t时刻的状态变量，f为连续可微函数，常数c为网络的耦合强度，H为各个节点状态变量之间的内耦合矩阵 [24] ，矩阵 $P_N={\left[p_{ij}\right]}_{N\times N}$ 表示网络中的外部耦合

矩阵，可以用来展示网络间的拓扑结构，并且满足耗散耦合条件 ${\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{ij}}=0$ ，其中网络的拓扑结构还可以

用图 $G=\left(\upsilon ,\epsilon \right)$ 来进行描述，节点集为 $\upsilon =\left\{1,2,\cdots ,N\right\}$ ，边缘集为 $\epsilon \subseteq \upsilon \times \upsilon$ ，矩阵 $P_N={\left[p_{ij}\right]}_{N\times N}$ 是图G的相应拉普拉斯矩阵，定义为：如果节点i和节点j之间有边连接，则 $p_{ij}=-1$ ，否则为0 [25] 。

本文针对的是多重边的复杂网络，根据节点之间信息传输速度的不同，通过引入时延对该网络进行拆分。在本文我们基于网络中边的不同性质的拆分原则，以许多子网络组合在一起的形式将多重边复杂网络进行拆分 [26] 。在此网络中有N个相同动力学系统的节点，假设网络中不同性质的边有 $k+1$ 种，w表示网络两个节点之间的最大重边数，拆分后的网络也可能具有多重边 [26] ，第l个子网的最大重边数为 $z_l\left(l=1,2,\cdots ,k\right)$ 且 $z_l\le w$ ，那么具有相同性质的边和N个节点所构成的子网络就会有 $k+1$ 个。其中对于传输速度最快的边和N个节点构成的网络为基准网络，即 ${\tau }_0=0$ ，其他剩余的边和N个节点所构成的l个子网络对于基准网络来说都存在时延 $\left(l=0,1,\cdots ,k\right)$ ，因此， $k+1$ 个子网络就划分成功。

下面是具有N个相同动力学系统的节点构成的含w重边的时延复杂网络模型，其中含有 $k+1$ 个不同性质的边。基于上述的拆分思想，我们将该网络 [21] 划分成 $k+1$ 个子网络，其中第i个节点的网络状态方程为：

$\begin{array}{c}{\stackrel{\dot{}}{x}}_i\left(t\right)=f\left(x_i\left(t\right),t\right)-c_0{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(0\right)}{}_{ij}}H{x}_j\left(t\right)-c_1{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(1\right)}{}_{ij}}H{x}_j\left(t-{\tau }_1\right)-c_2{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(2\right)}{}_{ij}}H{x}_j\left(t-{\tau }_2\right)\\ +\cdots -c_k{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(k\right)}{}_{ij}}H{x}_j\left(t-{\tau }_k\right)\end{array}$ (2)

其中： $x_i\left(t\right)={\left(x_{i1}\left(t\right),x_{i2}\left(t\right),\cdots ,x_{in}\left(t\right)\right)}^{\text{T}}\in R^n$ 是节点i在t时刻的状态变量， $i=1,2,\cdots ,N$ ， $f:R^n\to R^n$ 为连续可微的非线性向量函数； $c_l>0,l=1,\cdots ,k$ 为第l个子网络的耦合强度； $H\in R^n\times R^n$ 代表子网络中各个节点之间的内耦合矩阵(本文假设所有拆分后的子网络的内部耦合矩阵是相同的)，且为正定矩阵；矩阵

$P_{N\left(r\right)}={\left[p_{\left(r\right)}{}_{ij}\right]}_{N\times N}$ 表示第r个子网络的外部耦合矩阵，此处我们将其以拉普拉斯矩阵的形式表现出来， $r=0,1,\cdots ,k$ ，可以用来展示网络间的拓扑结构，并且满足耗散耦合条件，其中矩阵 $P_N={\left[p_{ij}\right]}_{N\times N}$ 定义如

下：如果节点i和节点j之间有边连接，则 $p_{\left(r\right)}{}_{ij}=p_{\left(r\right)}{}_{ji}=-1$ ，否则为0。

定义1当 $t\to \infty$ 时，孤立节点 $s\left(t\right)$ [14] 和各个节点 $x_i\left(t\right)$ 之间满足 $x_1\left(t\right)\to x_2\left(t\right)\to \cdots \to x_N\left(t\right)\to s\left(t\right)$ ，即：

$\underset{t\to \infty }{\lim }\Vert x_i\left(t\right)-s\left(t\right)\Vert =0,i=1,2,\cdots ,N.$ (3)

则称复杂网络趋于同步状态，其中对于孤立节点 $s\left(t\right)$ ，有：

$\stackrel{\dot{}}{s}\left(t\right)=f\left(s\left(t\right),t\right)$ (4)

定义误差向量为：

$e_i\left(t\right)=x_i\left(t\right)-s\left(t\right),i=1,2,\cdots ,N.$ (5)

接下来为使网络模型中的所有节点可以在一定的时间段内达到同步状态，我们选择对节点 $i=1,2,\cdots ,l$ 施加自适应牵制同步控制器( $1\le l<N$ )，因此被牵制的复杂网络模型(1)可以被重新描述为：

${\stackrel{\dot{}}{x}}_i\left(t\right)=f\left(x_i\left(t\right),t\right)-c_0{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(0\right)}{}_{ij}}H{x}_j\left(t\right)-{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(r\right)}{}_{ij}}H{x}_j\left(t-{\tau }_r\right)+u_i\left(t\right),i=1,2,\cdots ,l$

${\stackrel{\dot{}}{x}}_i\left(t\right)=f\left(x_i\left(t\right),t\right)-c_0{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(0\right)}{}_{ij}}H{x}_j\left(t\right)-{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(r\right)}{}_{ij}}H{x}_j\left(t-{\tau }_r\right),i=l+1,l+2,\cdots ,N.$ (6)

其中自适应牵制同步控制器为：

$u_i\left(t\right)=\{\begin{array}{l}-d_i\left(t\right)H{e}_i\left(t\right),1\le i\le l\\ 0,l+1\le i\le N\end{array}$ (7)

其中自适应更新律为： ${\stackrel{\dot{}}{d}}_i\left(t\right)=p_i{e}_i^{\text{T}}\left(t\right)H{e}_i\left(t\right)$ ， $p_i$ 是正常数( $1\le i\le l$ )。

因此，我们得到误差系统为：

${\stackrel{\dot{}}{e}}_i\left(t\right)=f\left(x_i\left(t\right),t\right)-f\left(s\left(t\right),t\right)-c_0{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(0\right)}{}_{ij}}H{e}_j\left(t\right)-{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(r\right)}{}_{ij}}H{e}_j\left(t-{\tau }_r\right)}+u_i(\; t\; )$

${\stackrel{\dot{}}{e}}_i\left(t\right)=f\left(x_i\left(t\right),t\right)-f\left(s\left(t\right),t\right)-c_0{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(0\right)}{}_{ij}}H{e}_j\left(t\right)-{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(r\right)}{}_{ij}}H{e}_j\left(t-{\tau }_r\right)}$ (8)

假设1 [14] 此处存在一个常数 $\vartheta$ ，有以下的不等式成立：

${\left(x-y\right)}^{\text{T}}\left(f\left(x\right)-f\left(y\right)\right)\le \vartheta {\left(x-y\right)}^{\text{T}}H\left(x-y\right),\forall x,y\in R^m$ (9)

其中 $\vartheta$ 为常数，所有向量 $x,y\in R^n$ 。

引理1 [27] 若 $B=\left[b_{ij}\right]$ 为一个 $N\times N$ 的实对称矩阵，则：

${\lambda }_1\left(B\right)\le \underset{1\le i\le N}{\min }\left[b_{ii}\right]\le \underset{1\le i\le N}{\max }\left[b_{ii}\right]\le {\lambda }_N\left(B\right)$ (10)

${\lambda }_1\left(B\right)$ 和 ${\lambda }_N\left(B\right)$ 分别表示矩阵B的最小特征值和最大特征值。

引理2 (Schur补引理 [20] )：假设矩阵 $U\left(x\right)=U^{\text{T}}\left(x\right)$ ， $W\left(x\right)=W^{\text{T}}\left(x\right)$ ，如果有以下的线性矩阵不等式给出：

$\left(\begin{array}{cc}U\left(x\right)& S\left(x\right)\\ S^{\text{T}}\left(x\right)& W\left(x\right)\end{array}\right)<0,$ (11)

与下面的条件之一等价：

$(1)U\left(x\right)<0,W\left(x\right)-S{\left(x\right)}^{\text{T}}U{\left(x\right)}^{-1}S\left(x\right)<0,$

$(2)W\left(x\right)<0,U\left(x\right)-S\left(x\right)W{\left(x\right)}^{-1}S{\left(x\right)}^{\text{T}}<0.$ (12)

引理3 (柯西交错定理 [28] )：A为一个 $N\times N$ 的实对称矩阵，B为实对称矩阵A通过删除行和列所对应的 $N-1$ 阶主子矩阵。在此处，让 ${\lambda }_i$ 和 ${\mu }_i$ 分别表示矩阵A和B的特征值，且 ${\lambda }_1\le {\lambda }_2\le \cdots \le {\lambda }_N$ ， ${\mu }_1\le {\mu }_2\le \cdots \le {\mu }_{N-1}$ 。则：

${\lambda }_1\le {\mu }_1\le {\lambda }_2\le {\mu }_2\le \cdots \le {\lambda }_{N-1}\le {\mu }_{N-1}\le {\lambda }_N$ (13)

引理4 [29] 对于任何的向量， $x,y\in R^m$ ，并且存在一个正定的矩阵 $W\in R^{m\times m}$ ，则会有以下的矩阵不等式成立：

$2x^{\text{T}}y\le x^{\text{T}}Wx+y^{\text{T}}{W}^{-1}y$ (14)

引理5 [30] 对于克罗内克积，满足如下性质：其中 $U\in R^{m\times n},Y\in R^{r\times s},Z\in R^{n\times p}$ ，其中 $P\in R^{s\times t}$ 。

$(1){\left(U\otimes Y\right)}^{\text{T}}=U^{\text{T}}\otimes Y^{\text{T}};$

$(2)\left(U\otimes Y\right)\left(Z\otimes P\right)=\left(UZ\right)\otimes \left(YP\right).$ (15)

引理6 [22] 若 $B=\left[b_{ij}\right]$ 为一个 $N\times N$ 的实对称矩阵且 ${\lambda }_1\left(B\right)\le \cdots \le {\lambda }_N\left(B\right)$ 。让 $\Vert x\Vert ={\left({\displaystyle {\sum }_{i=1}^N{x}_i^2}\right)}^{1/2}$ 。则：

${\lambda }_N\left(B\right)=\underset{\Vert x\Vert =1}{\max }\left[x^{\text{T}}Bx\right]$ (16)

3. 多重边复杂网络同步分析

3.1. 同步稳定性分析

定理1 在假设1成立的条件下，且存在适当的正常数 ${\gamma }_r\left(r=1,2,\cdots ,k\right)$ ，如果满足下面的条件：

${\lambda }_N\left(-c_0{P}_{\left(0\right)N-l}+\frac{{\lambda }_{\tau }}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r{P}_{\left(r\right)N-l}^2}\right)<-\vartheta -\frac{1}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}-{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\gamma }_r}$ (17)

( ${\lambda }_N$ 表示对称矩阵 $-c_0{P}_{\left(0\right)N-l}+\frac{\lambda }{2}{c}_r{\displaystyle \underset{r=1}{\overset{k}{\sum }}{P}_{\left(r\right)N-l}^2}$ 的最大特征值， ${\lambda }_{\tau }$ 表示矩阵H的最大特征值。)

那么多重边的复杂网络模型(6)在自适应牵制同步控制器(7)的作用下可以实现同步：

证明：构造Lyapunov-Krasovskii泛函为：

$V\left(t\right)=\frac{1}{2}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}\left(t\right)e_i}\left(t\right)+{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\displaystyle \underset{j=1}{\overset{N}{\sum }}{\gamma }_r{\displaystyle {\int }_{t-{\tau }_l}^t{e}_i^{\text{T}}}\left(t\right)H{e}_i}}\left(t\right)\text{d}t+\frac{1}{2}{\displaystyle \underset{i=1}{\overset{l}{\sum }}\frac{{\left(d_i\left(t\right)-d_{*}\right)}^2}{p_i}}$

沿误差系统(8)的任意轨线，并结合假设1， $V\left(t\right)$ 关于时间的导数为：

$\begin{array}{c}\stackrel{\dot{}}{V}\left(t\right)={\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}\left(t\right)}\left[f\left(x_i\left(t\right)\right)-f\left(s\left(t\right)\right)-c_0{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(0\right)ij}H{e}_j\left(t\right)}-{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}{\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(r\right)}H{e}_j\left(t-{\tau }_r\right)}-d_i\left(t\right)H{e}_i\left(t\right)\right]\\ +{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\displaystyle \underset{j=1}{\overset{N}{\sum }}{\gamma }_r}}{e}_i^{\text{T}}\left(t\right)H{e}_i\left(t\right)-{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\displaystyle \underset{j=1}{\overset{N}{\sum }}{\gamma }_r{e}_i^{\text{T}}}}\left(t-{\tau }_r\right)H{e}_i\left(t-{\tau }_r\right)+{\displaystyle \underset{i=1}{\overset{l}{\sum }}\left(d_i\left(t\right)-d_{*}\right)e_i^{\text{T}}\left(t\right)H{e}_i\left(t\right)}\\ \le \vartheta {\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}\left(t\right)H{e}_i\left(t\right)-c_0{\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}}\left(t\right){\displaystyle \underset{j=1}{\overset{N}{\sum }}{p}_{\left(0\right)}{}_{ij}H{e}_j\left(t\right)}-{\displaystyle \underset{i=1}{\overset{N}{\sum }}{e}_i^{\text{T}}\left(t\right)}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\displaystyle \underset{j=1}{\overset{N}{\sum }}{c}_r{p}_{\left(r\right)ij}}}H{e}_j\left(t-{\tau }_r\right)\\ -{\displaystyle \underset{i=1}{\overset{l}{\sum }}{d}_{*}}\left(t\right)e_i^{\text{T}}\left(t\right)H{e}_i\left(t\right)+{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\displaystyle \underset{j=1}{\overset{N}{\sum }}{\gamma }_r}}\cdot e_i^{\text{T}}\left(t\right)H{e}_i\left(t\right)-{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\displaystyle \underset{j=1}{\overset{N}{\sum }}{\gamma }_r{e}_i^{\text{T}}}}\left(t-{\tau }_r\right)H{e}_i\left(t-{\tau }_r\right)\end{array}$ (18)

此处使用引理4和引理5，可将上式变成如下形式：

$\begin{array}{c}\stackrel{\dot{}}{V}\left(t\right)\le \vartheta e^{\text{T}}\left(t\right)\left(I_N\otimes H\right)e\left(t\right)-c_0{e}^{\text{T}}\left(t\right)\left(P_{\left(0\right)N}\otimes H\right)e\left(t\right)+\frac{{\lambda }_{\tau }}{2}{\displaystyle \underset{l=1}{\overset{k}{\sum }}{c}_r{e}^{\text{T}}\left(t\right)\left(P_{\left(r\right)N}^2\otimes H\right)e\left(t\right)}\\ +\frac{1}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r{e}^{\text{T}}\left(t\right)\left(I_N\otimes H\right)e\left(t\right)}-e^{\text{T}}\left(t\right)\left(D_{*}\otimes H\right)e\left(t\right)+{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\gamma }_r{e}^{\text{T}}\left(t\right)}\left(I_N\otimes H\right)e\left(t\right)\\ -{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\gamma }_r{e}^{\text{T}}\left(t-{\tau }_r\right)}\left(I_N\otimes H\right)e\left(t-{\tau }_r\right)\\ \le -{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\displaystyle \underset{j=1}{\overset{N}{\sum }}{\gamma }_r{e}_i^{\text{T}}}}\left(t-{\tau }_r\right)H{e}_i\left(t-{\tau }_r\right)\\ +e^{\text{T}}\left(t\right)\left[\left(\vartheta I_N-c_0{P}_{\left(0\right)N}+\frac{{\lambda }_{\tau }}{2}{c}_r{\displaystyle \underset{r=1}{\overset{k}{\sum }}{P}_{\left(r\right)N}^2+\frac{1}{2}}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}{I}_N-D_{*}+{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\gamma }_r{I}_N}\right)\otimes H\right]e\left(t\right)\end{array}$ (19)

(其中 $e\left(t\right)=\left(e_1\left(t\right),e_2\left(t\right),\cdots ,e_N\left(t\right)\right)$ ， $D_{*}=diag\left(\underset{l}{\underset{︸}{\bar{d},\bar{d},\cdots ,\bar{d}}},0_{l+1},\cdots ,0_N\right)$ 。)

易知 $-{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\displaystyle \underset{j=1}{\overset{N}{\sum }}{\gamma }_r{e}_i^{\text{T}}}}\left(t-{\tau }_r\right)H{e}_i\left(t-{\tau }_r\right)<0$ ，并且基于李亚普诺夫稳定性理论，如果微分不等式 $\stackrel{\dot{}}{V}\left(t\right)<0$ ，那么便可证明复杂网络达到同步状态：当存在足够大的正常数 $d_{*}$ 使得对称矩阵 $\left(\vartheta I_{N-l}-c_0{P}_{\left(0\right)N-l}+\frac{{\lambda }_{\tau }}{2}{c}_r{\displaystyle \underset{r=1}{\overset{k}{\sum }}{P}_{\left(r\right)N-l}^2+\frac{1}{2}}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}{I}_{N-l}+{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\gamma }_r{I}_{N-l}}\right)\otimes H<0$ ，则复杂网络达到全局同步的状态。

令

$F=\vartheta I_N-c_0{P}_{\left(0\right)N}+\frac{{\lambda }_{\tau }}{2}{c}_r{\displaystyle \underset{r=1}{\overset{k}{\sum }}{P}_{\left(r\right)N}^2+\frac{1}{2}}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}{I}_N+{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\gamma }_r}{I}_N-D_{*}$ $F=\left[\begin{array}{cc}{F}_l-{\hat{D}}_{*}& M\\ M^T& F_{N-l}\end{array}\right]$ (20)

根据引理2，可以得到：

$\vartheta I_{N-l}+{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\gamma }_r{I}_{N-l}}-c_0{P}_{\left(0\right)N-l}+\frac{{\lambda }_{\tau }}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}{P}_{\left(r\right)N-l}^2+\frac{1}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}\cdot I_{N-l}<0$ ，即

${\lambda }_N\left(-c_0{P}_{\left(0\right)N-l}+\frac{{\lambda }_{\tau }}{2}{c}_r{\displaystyle \underset{r=1}{\overset{k}{\sum }}{P}_{\left(r\right)N-l}^2}\right)<-\vartheta -\frac{1}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}-{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\gamma }_r}$ ，由此得到多重边复杂网络模型(6)同步的准则，由此来衡量牵制方案的有效性。

(其中： $M={\left(m_{ij}\right)}_{l\times \left(N-l\right)}$ ， $\left(m_{ij}\right)=f_{ij}$ ， ${\hat{D}}_{*}=c\times diag\left(\underset{l}{\underset{︸}{d_1,d_2,\cdots ,d_l}}\right)$ ， $P_{\left(r\right)N-l}$ 表示删除受控节点后的对称子拉普拉斯矩阵， ${\lambda }_N$ 表示对称矩阵 $-c_0{P}_{\left(0\right)N-l}+\frac{{\lambda }_{\tau }}{2}{c}_r{\displaystyle \underset{r=1}{\overset{k}{\sum }}{P}_{\left(r\right)N-l}^2}$ 的最大特征值。)

定理2如果满足以下条件：

${\lambda }_{\max }\left(\frac{{\lambda }_{\tau }}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r{P}_{\left(r\right)N}^2}\right)+\frac{1}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}<-\vartheta -{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\gamma }_r}$ (21)

$\vartheta <-\frac{1}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}-{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\gamma }_r}$ (22)

则受控复杂网络(6)将会达到同步状态。

证明：

由 $F=\vartheta I_N-c_0{P}_{\left(0\right)N}+\frac{{\lambda }_{\tau }}{2}{c}_r{\displaystyle \underset{r=1}{\overset{k}{\sum }}{P}_{\left(r\right)N}^2+\frac{1}{2}}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}\cdot I_N+{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\gamma }_r{I}_N-D_{*}}$ 可以得到：

$F\le \left(\vartheta +c_0{\lambda }_{\max }\left(-P_{\left(0\right)N}\right)+{\lambda }_{\max }\left(\frac{{\lambda }_{\tau }}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r{P}_{\left(r\right)N}^2}\right)+{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\gamma }_r}+\frac{1}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}\right)I_N<0$ (23)

注1由条件看出当 $\vartheta <-\frac{1}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r}-{\displaystyle \underset{r=1}{\overset{k}{\sum }}{\gamma }_r}$ 时受控的含时延多重边的复杂网络才可以达到同步，但是在文

献 [14] 中由条件看出当 $\vartheta <0$ 的时候网络不需要施加任何的控制器就可以自身达到同步，而当 $\vartheta >0$ 时需要对部分节点加上控制器才可以使得网络达到同步，这一点与具有时延的多重边复杂网络是不同的。说明含时延的多重边复杂网络对网络的动力学要求比较严苛，同时也说明了普通复杂网络的牵制控制策略对于含时延的多重边复杂网络并不是完全适用的。

3.2. 牵制节点组的选择

定理3 令受控节点集 $v=\left\{i_1,i_2,\cdots ,i_l\right\}$ ，下面给出了删除受控节点集后对称子拉普拉斯矩阵和原矩阵的特征值关系：

${\lambda }_{N-1}\left[-c_0{P}_{\left(0\right)N-l}+\frac{{\lambda }_{\tau }}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r{P}_{\left(r\right)N-l}^2}\right]\ge {\lambda }_{N-l}\left[-c_0{P}_{\left(0\right)N}+\frac{{\lambda }_{\tau }}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r{P}_{\left(r\right)N}^2}\right]$ (24)

证明：结合引理3得到：

${\lambda }_{N-1}\left(P_{N-l}\right)\ge {\lambda }_{N-1}\left(P_N\right)\ge \cdots \ge {\lambda }_1\left(P_N\right)$ (25)

所以我们可以得出：

${\lambda }_{N-1}\left(P_{N-l}\right)\ge {\lambda }_{N-i}\left(P_N\right)\left(i=1,2,\cdots ,N-l\right)$ (26)

定理4 针对牵制不同的受控节点数，发现子矩阵的最大特征值随着受控节点个数的增多而减小。

$\max \left[{\lambda }_N\left(-c_0{P}_{\left(0\right)N-l}+\frac{{\lambda }_{\tau }}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r{P}_{\left(r\right)N-l}^2}\right)\right]\ge \max \left[{\lambda }_N\left(-c_0{P}_{\left(0\right)N-l-1}+\frac{{\lambda }_{\tau }}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r{P}_{\left(r\right)N-l-1}^2}\right)\right]$ (27)

证明：根据引理3得出：

${\lambda }_N\left(P_{N-l}\right)\ge {\lambda }_N\left(P_{N-l-1}\right)$ (28)

由此可以得到：

${\lambda }_N\left(-c_0{P}_{\left(0\right)N-l}+\frac{{\lambda }_{\tau }}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r{P}_{\left(r\right)N-l}^2}\right)\ge {\lambda }_N\left(-c_0{P}_{\left(0\right)N-l-1}+\frac{{\lambda }_{\tau }}{2}{\displaystyle \underset{r=1}{\overset{k}{\sum }}{c}_r{P}_{\left(r\right)N-l-1}^2}\right)$ (29)

定理5 在用来表示网络拓扑结构的图G中，其中 $DI\left(N\right)$ 表示所有节点的入度和， $D{k}_i$ 表示受控节点i的出入度和， ${\displaystyle \underset{i=1}{\overset{N-l}{\sum }}{p}_{ii}}$ 表示 $P_{N-l}$ 矩阵的对角线元素之和。则有：

$D{k}_i\le DI\left(N\right)+\left(N-l\right)\times {{\lambda }^{″}}_N-{\displaystyle \underset{i=1}{\overset{N-l}{\sum }}{\tilde{h}}_{ii}}-{\displaystyle \underset{i=1}{\overset{l-1}{\sum }}D{k}_i}$ (30)

证明：此处， $a_0=\left(1/\left(N-l\right)\right){\left(1,\cdots ,1\right)}^{\text{T}}$ 为一个 $\left(N-l\right)$ 行1列的向量，由引理6我们得到：

$\begin{array}{c}{\lambda }_N\left(P_{N-l}\right)=\underset{\Vert x\Vert =1}{\max }\left[a^{\text{T}}L\left(J\right)a+a^{\text{T}}\Lambda a\right]\\ \ge x_0^{\text{T}}L\left(J\right)x_0+x_0^{\text{T}}\Lambda x_0\\ \ge \frac{DO\left(I\right)-b}{N-l}\\ \ge \frac{DO\left(I\right)}{N-l}\end{array}$

$\iff DO\left(I\right)\le \left(N-l\right)\times {\lambda }_N\left(P_{N-l}\right)$

$\iff DO\left(N\right)-DS\left(N\right)+DI\left(M\right)+DS\left(I\right)\le \left(N-l\right)\times {{\lambda }^{″}}_N$

$\iff DS\left(I\right)\le DI\left(N\right)-DI\left(M\right)-\left(N-l\right)\times {{\lambda }^{″}}_N$

$\iff DS\left(I\right)\le DI\left(N\right)-{\displaystyle \underset{i=1}{\overset{N-l}{\sum }}{\tilde{l}}_{ii}}+\left(N-l\right)\times {{\lambda }^{″}}_N$

$\iff D{k}_1+D{k}_2+\cdots +D{k}_l\le DI\left(N\right)-{\displaystyle \underset{i=1}{\overset{N-l}{\sum }}{\tilde{l}}_{ii}}+\left(N-l\right)\times {{\lambda }^{″}}_N$ (31)

(DO表示节点的出度和，DS表示节点的出入度和，I、M、N分别表示受控节点集、未受控节点集和所有节点，b表示受控节点集之间的出度和。 $L\left(J\right)$ 表示未受控节点的对称拉普拉斯矩阵。 $\Lambda =diag\left(DO\left(i{m}_1\right),\cdots ,DO\left(i{m}_{N-l}\right)\right)$ ，其中 $DO\left(i{m}_j\right)$ 表示受控节点集到未受控节点的出度和。)

注2

1) 将实对称矩阵 $B\in N\times N$ 的特征值按照依次递增的顺序进行排列：

${\lambda }_1\left(B\right)\le {\lambda }_2\left(B\right)\le \cdots \le {\lambda }_{N-l}\left(B\right)\le {\lambda }_N\left(B\right)$ (32)

2) 在节点总数为N的复杂网络中， $I=\left\{i_1,\cdots ,i_l\right\}$ 表示多重边复杂网络中受牵制的节点集， $M=\left\{m_{l+1},\cdots ,m_{N-l}\right\}$ 表示该网络中未受牵制的节点集。

3) 通过该定理，我们可以对一些不符合条件的节点进行筛选，从而减少计算量。从中我们可以看出，针对时延复杂网络，会优先选择度比较小的节点而放弃度比较大的节点，这与一般复杂网络是不同的。

算法步骤：

步骤1：在找到满足牵制条件的候选节点的基础上，由此可以对节点进行排序：首先是 $DI\left(i\right)=0$ 的节点，接下来的节点按照 $DO\left(i\right)$ 依次递减的的顺序进行排列。如果其中有某些节点的 $DO\left(i\right)$ 相同，那么这些节点按照 $DS\left(i\right)$ 依次递减的顺序进行排列。这样对网络中的节点进行初步筛选后，继续对节点组的重要性排序进行研究。(其中 $DS\left(i\right)=DO\left(i\right)-DI(\; i\; ))$

步骤2：按照步骤1对节点进行排序后，结合此时所需要的牵制节点数量，将排序的前l个节点作为初始节点，计算这些节点对应的 ${\lambda }_N$ ，依此作为最初的 ${{\lambda }^{″}}_N$ 。

步骤3：基于多重边复杂网络中受控节点的度对所有节点进行筛选，从而找到符合定理5的节点集。

步骤4：对所有节点进行筛选后，对剩余的节点进行组合，计算不同节点组所对应的 ${\lambda }_N$ ，从而找到最大的 ${\lambda }_N$ ，进而优化网络的牵制效果。

4. 数值仿真

为了验证前面的理论结果，在本章节我们考虑有三种性质的复杂网络来进行仿真研究。

${\stackrel{\dot{}}{x}}_i\left(t\right)=f\left(x_i\left(t\right),t\right)-c_0{\displaystyle \underset{j=1}{\overset{10}{\sum }}{p}_{\left(0\right)}{}_{ij}}H{x}_j\left(t\right)-c_1{\displaystyle \underset{j=1}{\overset{10}{\sum }}{p}_{\left(1\right)}{}_{ij}}H{x}_j\left(t-{\tau }_1\right)-c_2{\displaystyle \underset{j=1}{\overset{10}{\sum }}{p}_{\left(2\right)}{}_{ij}}H{x}_j\left(t-{\tau }_2\right)$ (33)

该网络由10个节点组成，第i个节点的动力学方程为：

$f\left(x_i\right)=\{\begin{array}{c}-30x_{i1}\\ -60x_{i2}+x_{i1}{x}_{i3}\\ -30x_{i3}-x_{i1}{x}_{i2}\end{array}$ (34)

结合假设1我们可以得到：

$\begin{array}{l}{\left(x_i-s\right)}^{\text{T}}\left(f\left(x_i\right)-f\left(s\right)\right)\\ =\left[e_{i1}{e}_{i2}{e}_{i3}\right]\left[\begin{array}{c}-30e_{i1}\\ -60e_{i2}+s_1{e}_{i3}+s_3{e}_{i1}+e_{i1}{e}_{i3}\\ -30e_{i3}-s_1{e}_{i2}-s_2{e}_{i1}-e_{i1}{e}_{i2}\end{array}\right]\\ =-30e_{i1}^2-60e_{i2}^2-30e_{i3}^2+s_3{e}_{i1}-s_2{e}_{i1}\\ =-30\left(e_{i1}^2+2e_{i2}^2+e_{i3}^2\right)\le \vartheta e_i^{\text{T}}H{e}_i\end{array}$ (35)

在该仿真系统中，内部耦合矩阵 $H=diag\left(1,2,1\right)$ ，选择 $\vartheta =-20$ 满足假设1的条件。耦合强度 $c_0=c_1=0.2$ ， $c_2=0.1$ ， ${\gamma }_1={\gamma }_2=1$ ，信息传输的时延 ${\tau }_1=1$ ， ${\tau }_2=2$ ，最大重边数 $w_0=w_1=w_2=1$ ，外部耦合矩阵 $P_{\left(0\right)},P_{\left(1\right)},P_{\left(2\right)}$ 分别为

$P_{\left(0\right)}=P_{\left(1\right)}=\left[\begin{array}{cccccccccc}2& 0& 0& -1& 0& 0& 0& -1& 0& 0\\ 0& 4& -1& -1& 0& 0& -1& 0& -1& 0\\ 0& -1& 6& -1& 0& -1& -1& 0& -1& -1\\ -1& -1& -1& 3& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 2& 0& -1& 0& -1& 0\\ 0& 0& -1& 0& 0& 1& 0& 0& 0& 0\\ 0& -1& -1& 0& -1& 0& 5& -1& 0& -1\\ -1& 0& 0& 0& 0& 0& -1& 3& -1& 0\\ 0& -1& -1& 0& -1& 0& 0& -1& 5& -1\\ 0& 0& -1& 0& 0& 0& -1& 0& -1& 3\end{array}\right]$

$P_{\left(2\right)}=\left[\begin{array}{cccccccccc}4& -1& 0& -1& 0& -1& 0& 0& -1& 0\\ -1& 3& 0& 0& -1& 0& 0& -1& 0& 0\\ 0& 0& 6& -1& -1& 0& -1& -1& -1& -1\\ -1& 0& -1& 2& 0& 0& 0& 0& 0& 0\\ 0& -1& -1& 0& 5& 0& -1& 0& -1& -1\\ -1& 0& 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& -1& 0& -1& 0& 5& -1& -1& -1\\ 0& -1& -1& 0& 0& 0& -1& 5& -1& -1\\ -1& 0& -1& 0& -1& 0& -1& -1& 6& -1\\ 0& 0& -1& 0& -1& 0& -1& -1& -1& 5\end{array}\right]$

基于上述算法，我们将所有节点进行排列：3、9、7、8、10、2、5、1、4、6。

通过仿真，我们验证了对于时延复杂网络的节点组的选择不同于一般的网络，为使牵制效果更好，它会优先牵制度比较小的节点。下面画出了当牵制七个节点时候的同步误差图1，以及随着受控节点个数的增加特征值谱特性的变化趋势图2。

Figure 1. Synchronization error diagram of complex network (6) under adaptive controller (7) when the number of pinning nodes $l=7$

图1. 牵制节点数 $l=7$ 时，复杂网络(6)在自适应控制器(7)下的同步误差图

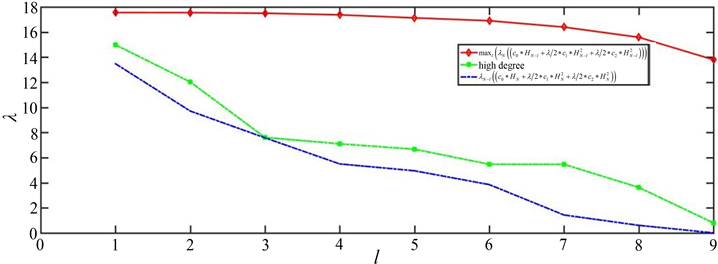
Figure 2. With the increase of the number of controlled nodes l, $\max \left({\lambda }_N\right)$ large nodes and ${\lambda }_{N-l}$ change trend chart

图2. 随着受控节点个数l的增加， $\max \left({\lambda }_N\right)$ 、度大的节点和 ${\lambda }_{N-l}$ 变化趋势图

1) 当牵制3个节点时，选取排序中的前3个节点{3、9、7}，此时 ${\lambda }_N=7.6100$ ；但是根据上述算法，我们计算出当牵制节点组{10、2、1}时， ${\lambda }_N=17.6647$ 更大，此时牵制效果会更好。

2) 当牵制5个节点时，选取排序中的前5个节点{3、9、7、8、10}，此时 ${\lambda }_N=6.6727$ ；但是根据上述算法，我们计算出当牵制节点组{10、2、5、1、6}时， ${\lambda }_N=17.2756$ ；更大，此时牵制效果会更好。

下面给出了牵制节点个数为 $l=7$ 自适应控制器下的同步误差图以及相应的最优受控节点集。

当 $l=7$ 时： $\max \left[{\lambda }_N\left(c_0{P}_{\left(0\right)N-l}+\frac{{\lambda }_{\tau }}{2}{c}_1{P}_{\left(1\right)N-l}^2+\frac{{\lambda }_{\tau }}{2}{c}_2{P}_{\left(2\right)N-l}^2\right)\right]=16.5264$ ，当选取排序中的前7个节点{3、9、7、8、10、2、5}进行牵制时，其所对应的： ${\lambda }_N\left(c_0{P}_{\left(0\right)N-l}+\frac{{\lambda }_{\tau }}{2}{c}_1{P}_{\left(1\right)N-l}^2+\frac{{\lambda }_{\tau }}{2}{c}_2{P}_{\left(2\right)N-l}^2\right)=5.4686$ ，然而基于本文的理论，我们发现当节点8、10、2、5、1、4、6时， ${\lambda }_N$ 更大，使得牵制效果更好。

5. 结论

本文针对多重边网络的节点集优化进行了研究，并且引入了时延，使得所研究的模型更加广泛、符合实际。通过应用Lyapunov稳定性理论、自适应控制方法，在给出具有时延的多重边复杂网络全局同步的准则后，又结合图论和矩阵分析等工具，通过删除网络的对称拉普拉斯矩阵中需要牵制节点所对应的行和列，从而得到新矩阵的最大特征值，同时结合网络的拓扑信息分析了最大特征值的谱特性，找到最优的受控节点组，以此来实现更好的牵制同步效果。最后通过数值仿真对本文得到的理论结果的准确性和有效性进行了验证。

致谢

本文受到了辽宁省教育厅科学研究项目(Injc202018)，全国大学生创新创业训练计划校级项目(D202203180905324690)的支持。