具有不同故障和延迟维修的重试队列的优化分析

Optimization Analysis of Retrial Queues with Different Breakdowns and Delayed Repairs

摘要: 本文研究具有两种类型故障和延迟维修的M/M/1重试队列。在稳态条件下，我们得到了服务台状态和轨道顾客数的概率母函数的表达式。建立了以期望成本最小化和顾客期望等待时间最小化为目标的双目标优化模型。拟议的分析办法使我们能够在成本费用和服务质量之间取得适当的平衡。

Abstract: In this paper we study M/M/1 retrial queues with two types of breakdowns and delayed repairs. Under steady-state conditions, we obtain expressions for the probability generating functions of the server state and the number of orbital customers. A bi-objective optimization model with the objectives of minimizing the expected cost and minimizing the expected waiting time of the customers is developed. The proposed analytical approach allows us to achieve an appropriate balance between operational costs and service quality.

1. 引言

重试排队的通用模型、方法、结果，示例和应用可以在Artalejo和Corral [1] 以及Tian和Zhang [2] 中找到。由于现实中一些不可预知的因素，如服务器寿命有限、外部干扰、服务器故障、启动失败等，在空闲或忙碌期间，服务器可能会出现故障并需要维修。Kulkarni和Choi [3] 介绍了服务器受到故障和维修的重试队列，并得出了系统的稳定条件和稳态分布。此后，对故障和可修的重试排队从稳定性和可靠性的角度进行广泛研究。Zhang等 [4] 研究了具有两类故障和延迟修复的M/G/1重试队列分析，通过补充变量法计算出一些重要的性能指标和可靠性指标。Krishna等 [5] 研究了具有两种故障和维修的马尔科夫重试队列。

大多数关于排队模型优化的研究都集中在单目标问题上，然而现实世界中有许多优化问题需要同时考虑多个目标函数。Tavakkoli等 [6] 提出了一种新的多目标模型，用于解决具有拥堵和定价策略的设施位置问题。该模型考虑了不移动服务设施因M/M/m/k队列之后的随机需求而拥堵的情况。Wu和Yang [7] 研究了具有两阶段异构服务排队模型的双目标优化问题。Khodemani等 [8] 提出了一个双目标分层枢纽选址问题，旨在同时使总成本和总行程时间最小化。他们分别使用M/M/C和M/M/1排队系统来模拟中心和本地枢纽的队列。Hajipour [9] 研究具有固定服务器和随机需求为M/M/M/K的拥塞系统队列的双目标优化问题。更多关于多目标优化的问题，可以参阅文献 [10] [11] [12] 。

2. 模型描述

在具有负顾客、被动故障和延迟维修的重试队列中。顾客根据速率 $\lambda$ 的泊松过程到达系统。服务台的服务速率服从参数为 $\mu$ 的指数分布。到达顾客发现服务台不可用就会以概率q加入轨道或以互补概率 $1-q$ 离开系统。重试时间服从参数为v的指数分布。服务台可能会遇到两种类型的故障，即被动故障和主动故障。被动故障意味着当服务台处于空闲状态时系统根据速率为 $\eta$ 的泊松过程发生故障。被动故障的修复时间服从参数为 $\theta$ 的指数分布，由于在空闲期间缺乏对服务台的监控，当发生被动故障时服务台无法立即获得修复，而处于延迟修复状态。延迟维修服从参数为 $\delta$ 的指数分布。主动故障意味着当服务台繁忙时，负面顾客的到来会影响系统，导致服务台故障，同时迫使正在服务的顾客离开系统。负顾客根据速率为 $\phi$ 的泊松过程到达。主动修复时间服从参数为 $\beta$ 指数分布。

最后，假设到达、服务、故障、修复、延迟维修和重试过程相互独立。

令 $N\left(t\right)$ 表示时刻t轨道中的顾客数， $I\left(t\right)$ 表示时刻t系统的状态(0：服务台空闲，1：服务台繁忙，2：服务台处于被动故障状态，3：服务台处于主动故障状态，4：服务台处于延迟修复状态)。

3. 稳态分析

$\pi \left(j,i\right)$ 表示系统处于状态的加入概率。

$\pi \left(j,i\right)=\underset{t\to \infty }{\lim }P\left\{N\left(t\right)=j,I\left(t\right)=i\right\},\left(j,i\right)\in \Omega .$

为了获得系统稳态分布，我们定义概率母函数

$G_i\left(z\right)={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\pi \left(j,i\right)z^j},\left|z\right|<1,i\in \left\{0,1,2,3,4\right\}.$

服务台处于空闲状态的概率为

$P_0=G_0\left(1\right)=\frac{\mu \nu \theta \delta {\kappa }_1\left(\lambda q+\theta \right)\left(\lambda q+\delta \right)+\beta \phi \theta \delta \mu {\kappa }_2}{{\kappa }_2\left[\theta \delta {\kappa }_1\left(\lambda +\nu \right)-\beta \mu \lambda {\kappa }_3\right]}\pi \left(0,1\right)$ (1)

服务台繁忙的概率为

$P_1=G_1\left(1\right)=\frac{\beta \mu \lambda \nu {\kappa }_3\left(\lambda q+\theta \right)\left(\lambda q+\delta \right)+\beta \phi \theta \delta \mu {\kappa }_2\left(\lambda +\nu \right)}{{\kappa }_2\left[\theta \delta {\kappa }_1\left(\lambda +\nu \right)-\beta \mu \lambda {\kappa }_3\right]}\pi \left(0,1\right)$ (2)

服务台处于被动修复状态的概率为

$P_2=G_2\left(1\right)=\frac{\mu \nu \delta \eta {\kappa }_1\left(\lambda q+\theta \right)\left(\lambda q+\delta \right)+\beta \phi \delta \mu \eta {\kappa }_2}{{\kappa }_2\left[\theta \delta {\kappa }_1\left(\lambda +\nu \right)-\beta \mu \lambda {\kappa }_3\right]}\pi \left(0,1\right)$ (3)

服务台处于主动修复状态的概率为

$P_3=G_3\left(1\right)=\frac{\phi \mu \lambda \nu {\kappa }_3\left(\lambda q+\theta \right)\left(\lambda q+\delta \right)+{\phi }^2\theta \delta {\kappa }_2\left(\lambda +\nu \right)}{{\kappa }_2\left[\theta \delta {\kappa }_1\left(\lambda +\nu \right)-\beta \mu \lambda {\kappa }_3\right]}\pi \left(0,1\right)$ (4)

服务台处于延迟修复状态的概率为

$P_4=G_4\left(1\right)=\frac{\mu \nu \theta \eta {\kappa }_1\left(\lambda q+\theta \right)\left(\lambda q+\delta \right)+\beta \phi \theta \eta \mu {\kappa }_2}{{\kappa }_2\left[\theta \delta {\kappa }_1\left(\lambda +\nu \right)-\beta \mu \lambda {\kappa }_3\right]}\pi \left(0,1\right)$ (5)

其中

${\kappa }_1=\beta \left(\phi +\mu \right)-\lambda q\left(\beta +\phi \right)$

${\kappa }_2=\lambda \left[\lambda q\left(\lambda q+\eta q+\theta +\delta \right)+\eta q\left(\theta +\delta \right)+\theta \delta \right]$

${\kappa }_3=\eta q\left(\theta +\delta \right)+\theta \delta$

$A_1=\nu {\kappa }_1\left(\lambda q+\theta \right)\left(\lambda q+\delta \right)+\beta \phi {\kappa }_2$

$A_2=\lambda \mu \nu {\kappa }_3\left(\lambda q+\theta \right)\left(\lambda q+\delta \right)+\phi \theta \delta {\kappa }_2\left(\lambda +\nu \right)$

$\pi \left(0,1\right)=\frac{{\kappa }_2\left[\theta \delta {\kappa }_1\left(\lambda +\nu \right)-\beta \mu \lambda {\kappa }_3\right]}{\mu \left[\theta \delta +\eta \left(\theta +\delta \right)\right]A_1+\left(\beta +\phi \right)A_2}$ (6)

服务台空闲、繁忙、被动修复、主动修复、延迟修复时的平均轨道大小 $N_i$ 分别为

$N_0={G^{\prime }}_0\left(1\right)={\left({\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\pi \left(j,0\right)z^j}\right)}^{\prime }$ (7)

$N_1={G^{\prime }}_1\left(1\right)={\left({\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\pi \left(j,1\right)z^j}\right)}^{\prime }$ (8)

$N_2={G^{\prime }}_2\left(1\right)={\left({\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\pi \left(j,2\right)z^j}\right)}^{\prime }$ (9)

$N_3={G^{\prime }}_3\left(1\right)={\left({\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\pi \left(j,3\right)z^j}\right)}^{\prime }$ (10)

$N_4={G^{\prime }}_4\left(1\right)={\left({\displaystyle \underset{j=0}{\overset{\infty }{\sum }}\pi \left(j,4\right)z^j}\right)}^{\prime }$ (11)

设 $E\left(N\right)$ 表示轨道中顾客的平均数量。因此，

$E\left(N\right)=N_0+N_1+N_2+N_3+N_4$ (12)

假设被标记顾客在到达时发现服务台不可用，并决定加入重试轨道，他在轨道上的预期等待时间为

$W=\frac{E\left(N\right)}{{\lambda }_{ret}}=\frac{E\left(N\right)}{\lambda q\left[G_1\left(1\right)+G_2\left(1\right)+G_3\left(1\right)+G_4\left(1\right)\right]}$ (13)

4. 双目标优化

大多数关于排队模型优化设计的研究都集中在单目标问题上，其中成本或利润函数是优化目标。然而，现实世界中有许多优化问题需要同时优化多个目标函数。多方面考虑是决策所必需的。预期等待时间是决定顾客对服务质量满意度的最重要因素。在排队系统中，成本往往与服务质量相冲突。另一方面，系统对成本和服务质量的要求是不同的。通过分析我们观察到服务率 $\mu$ 和延迟修复率 $\delta$ 对预期等待时间W的影响较大，同时也会影响系统的预期成本。在本节中，我们借助遗传算法寻找同时满足最小成本和最少等待时间的Pareto最优解集。制定了一个双目标优化模型，旨在同时最小化期望成本 $F_p$ 和预期等待时间 $W_p$ 。

单位时间的期望成本函数为

$F\left(\mu ,\delta \right)=C_{h}E\left(N\right)+C_s\mu +C_e\delta +C_o{P}_1+C_f{P}_2+C_a{P}_3+C_i{P}_4$ (14)

其中 $C_h$ 是系统中每个顾客的持有成本， $C_s$ 是单位时间内提供服务的成本， $C_e$ 是单位时间延迟修复的成本， $C_o$ 是保持系统运行的单位时间成本， $C_f$ 是服务台处于被动故障状态的单位时间成本， $C_a$ 是服务由于负顾客而处于故障状态的单位时间成本， $C_i$ 是服务台处于延迟修复状态的单位时间成本。

双目标优化问题表述为

$\min \left[F_p{W}_p\right]$ (15)

多目标遗传算法是用来分析和解决多目标优化问题的一种进化算法，是以遗传算法为基础并基于Pareto最优概念得到的。其核心就是协调各个目标函数之间的关系，找出使得各个目标函数都尽可能达到比较小的(或者比较大的)函数值的最优解集。我们选择以下系统参数 $q=0.4$ ， $\phi =0.5$ ， $\beta =1.4$ ， $\eta =0.2$ ， $\theta =1.5$ ， $\nu =1.8$ ， $C_h=0.5$ ， $C_s=2$ ， $C_e=2.5$ ， $C_o=3$ ， $C_f=4$ ， $C_a=4$ ， $C_e=4.5$ 。图1给出了 $\lambda =2.2,2.4,2.6$ 时使用多目标遗传算法得到的非支配解，各种 $\lambda$ 值下的Pareto最优解汇总在表1中。这些结果为决策者提供了有用的指导方针。由图1和表1可以看出：

1) 这三条曲线表明，成本的增加导致顾客等待时间的减少。当 $W_p$ 固定时， $F_p$ 随着平均到达率 $\lambda$ 的增加而增加。

2) 当 $W_p$ 趋近无穷大时，最小期望成本 $F_p$ 收敛于某一值，该值可视为最小成本。

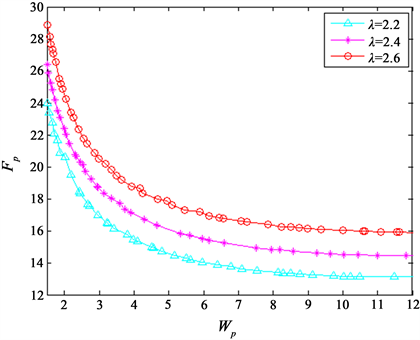
Figure 1. Pareto front solution found by genetic algorithm

图1. 遗传算法找到的Pareto前沿解

Table 1. The Pareto optimal solutions for various values of λ

表1. 不同参数 $\lambda$ 下的Pareto最优解

从表2中可以看出，单个自变量t检验的P值都小于0.01，回归方程F检验的P值小于0.01，因此，在0.01的显著水平下，各自变量对因变量的影响和回归方程都有显著的统计学意义。调整后的拟合优度为 $R^2=0.996$ ，模型拟合效果良好。

Table 2. Regression results

表2. 回归结果

注：^***表示系数在1%的水平下显著，括号内为标准误差。

从图1中可以看出 $F_p$ 与 $W_p$ 之间的关系是呈反比关系，近似为一个负指数的指数函数， $F_p$ 与 $\lambda$ 成正比关系。从图2回归残差的直方图中可以看出左右两侧对称，从K-S正态性检验图中可以看出，散点基本靠近直线。明预期累计概率与实测累计概率十分吻合，说明服从正态分布，满足回归的假设条件，可以建立回归关系。

因此，建立多元线性回归模型如下

$F_P=-8.039+8.846\lambda +13.694W_P^{-1}+18.712e^{-W_p}$ (16)

这个回归模型将有助于管理人员寻求在给定的 $\lambda$ 估计值下达到满意的服务水平所需的最小成本。

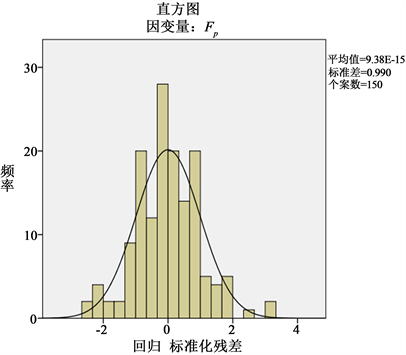
Figure 2. Histogram and K-S normality test for the regression residuals

图2. 回归残差的直方图和K-S正态性检验

5. 结论

我们研究了M/M/1重试排队系统，该系统具有延迟维修的被动故障和繁忙时期由负顾客引起的主动故障。利用概率母函数，我们得到了重要的性能指标。制定了一个基于性能指标和成本要素的成本函数，考虑了双目标优化问题，使用遗传算法最小化期望成本函数和预期等待时间，最后得到的Pareto最优解集。表明需要在运营成本和顾客等待时间之间进行权衡。