1. 引言
地下水封洞室在爆破开挖时，爆破附近区域内的岩体内部质点产生振动，引起岩体质点产生振动的弹性波称为地震波。当采用爆破方式开挖时，常常会通过增大爆破炸药量或提高爆破频率的方式提高效率 [1] 。在爆源区的一定范围内，爆破地震波会引起洞室邻近围岩的劣化，从而造成安全隐患甚至安全事故 [2] [3] ，这种由爆破产生的地震波引起的破坏现象称为爆破地震效应。
关于地下水封洞室爆破开挖产生的围岩振动效应，国内外学者进行了大量的研究。Nima Babanouri等 [4] 采用线性叠加与数值仿真模拟分析，提出一种研究爆破地震波传播的方法；Ma G. W等 [5] 运用数值仿真软件，研究爆破地震波在围岩中的传播规律；曹攀 [6] 利用离散元数值模拟软件，研究了岩体中爆炸应力波的衰减变化规律；谢烽 [7] 等建立了隧道爆破附近区域的振速计算模型，得出了爆破附近区域围岩的振动规律；史秀志等 [8] 监测施工现场的振动信号，得出了抵抗线大小和单段药量对爆破振动幅值及频率的影响；Resende等 [9] 结合现场监测与数值模拟结果，得出应力波传播途径和局部峰值在爆破地震波传播过程中起到关键控制作用；Mobaraki B [10] 研究了不同断面形状隧道在爆破荷载作用下的动态响应；Kim S等 [11] 研究了岩体节理方向与多条节理之间间距对于地震波及其衰减规律的影响；赵坚 [12] 通过采用AUTO-DYNA与UDEC两种软件研究了爆炸应力波在预存节理岩体中的传播过程；杨建华 [13] 对存在不同自由面的工况下爆破产生振动规律进行分析，得出了不同自由面对振动频率的影响规律；郑心铭等 [14] 通过现场实测数据，研究了隧洞爆破开挖产生围岩质点振速与频率的衰减规律；闫长斌 [15] 借助FLAC 3D软件分析了爆破震动对地下采空区的稳定性，模拟得到了围岩的塑性区范围、位移量以及应力分布等情况；杨建华 [16] 等运用ANSYS/LS-DYNA进行数值模拟，发现爆炸动荷载作用下，围岩主要呈现张拉破坏，但本身的地应力对爆破张拉效应起到一定的抑制作用；范宇 [17] 等运用3DEC开展了爆破动力荷载作用下水平层状岩层隧道成型影响因素研究，讨论了不同结构面间距、结构面结合程度以及岩体强度对隧道超挖量的影响；杨建华 [18] 等运用LS-DYNA有限元数值模拟研究了不同地应力水平下，爆破开挖诱发围岩损伤机理以及爆破损伤PPV阈值的变化规律。
2. 研究方法与试验设计
2.1. 研究思路
本文依托某地下水封洞室施工巷道爆破施工工程，结合项目工程地质条件与现场爆破方案，获取爆破动力时程曲线，研究依托工程施工巷道单洞围岩动力响应，具体研究思路如下：
(1) 对工程现场进行地质勘测调查，分析施工巷道施工中最危险横断面，同时通过钻孔取芯试验获取该横断面岩层分布情况及岩体力学参数。
(2) 结合现场实际爆破设计方案，采用动力有限元软件进行爆破数值仿真，获取爆破响应时程曲线。
(3) 运用离散元数值模拟软件，对施工巷道模型爆破开挖过程进行数值模拟，探索爆破扰动作用下施工巷道围岩塑性区、位移量、最大主应力及最大剪应变分布情况，及不同爆心距的各向振速峰值衰减曲线及规律。
2.2. 依托工程概况
本文依托的某地下水封洞库建设规模为300 × 104 m3，现场施工共布置2条施工巷道，施工巷道截面为直墙圆工形，洞室高度为9 m，跨度为10 m。
本次数值模拟选取K0 + 500.70 m横断面，该横断面岩层分布情况如图1所示，各岩体力学参数如表1所示。
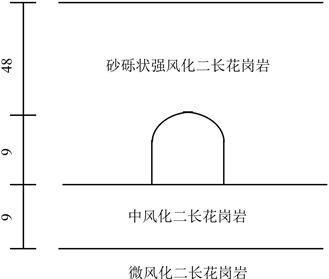
Figure 1. Schematic diagram of distribution of strata in K0 + 500.70 m cross-section
图1. K0 + 500.70 m横断面岩层分布示意图
Table 1. Related parameters of rock mechanics
表1. 岩体力学相关参数
3. 爆破响应时程曲线获取
3.1. 现场爆破方案设计
根据本工程的环境、地质及设计要求，洞口可能出现的中风化二长花岗岩，采用露天浅孔爆破法开挖；洞身采用新奥法开挖，应用光面爆破技术控制洞壁的超欠挖。施工巷道由于断面较小，采用全断面一次爆破，采用三臂凿岩台车水平向钻孔，钻孔深度一般为2.5 m~3.5 m，孔径一般为45 mm。平台作业车辅助人工安装炸药，非电毫秒雷管起爆。一次爆破的进尺一般在2.3 m~3.5 m。爆破采用2#岩石成品乳化炸药，所使用的炸药直径主要为φ32 mm，标准长度均为30 cm/节。雷管采用非电毫秒雷管及部分电子雷管，起爆采用非电毫秒雷管起爆方式。
根据施工巷道、连接巷道断面规格及施工经验采用楔形复式掏槽，掏槽眼深度为1.75 m、2.82 m、3.94 m、3.73 m、3.59 m、3.51 m，掏槽眼布置在断面中下部。主掏槽眼眼口间距2.4米，掏槽眼爆破角度为59˚、63˚、63˚、70˚、77˚；周边眼间距取0.5 m，深度取3.5 m；辅助眼间距取0.8 m~1.1 m，深度取3.5 m；底板眼间距取0.8 m，深度取3.5 m。
经过计算，此次爆破方案每循环进尺为3 m，循环爆破量：237.9 m3、炸药单耗：1.345 kg/m3。
根据萨式公式计算允许最大单段装药量：
取R = 110、K = 129.9053、α = 1.6088、V = 1.4
(1)
最大单段装药量为辅助孔17段49.35 kg < 允许量。
爆破设计图与开挖爆破参数如图2与表2所示。
Figure 2. Blasting design diagram (unit: cm)
图2. 爆破设计图(单位：cm)
Table 2. Excavation blasting parameter list
表2. 开挖爆破参数表
3.2. 爆破参数选取
在传统数值模拟中，将爆源近点实测质点振动速度时程波形作为动荷载输入到洞室开挖轮廓面周边，这种方法更贴近于实际情况，但也更加复杂。要实现炮孔周边处的围岩振速数据监测，现有的现场检测技术手段很难实现。于是基于上述现场实际工况及爆破方案，通过动力有限元软件获取爆源附近孔壁质点的三向振动速度时程曲线，为后续的数值模拟分析提供依据。
本次数值模拟炸药选取*MAT_HIGH_EXPLOSIVE_BURN模型，JWL状态方程得出爆轰压力的表达式为：
(2)
式中，P为爆轰压力；A、B、R1、R2为炸药相关常数；E0为炸药单位体积内能；V为相对体积。
由于现场爆破炸药采用了2#岩石乳化炸药，本文数值模拟选取的高能炸药材料相关参数设置以及JWL状态方程相关参数如表3、表4所示：
Table 3. Relevant parameters of high explosives
表3. 高能炸药相关参数
Table 4. JWL state equation related parameters
表4. JWL状态方程相关参数
采用*MAT_NULL材料模型来模拟空气材料，状态方程*EOS_LINEAR_POLYNOMIAL来描述具有流体行为的材料。E0，V0多项式状态方程的压力表达式如下：
(3)
式中：μ为空气当前密度与初始密度的比值；C0~C6为相关参数。
本次数值模拟设置空气模型及状态方程的参数值如表5、表6所示：
Table 5. Air model material related parameters
表5. 空气模型材料相关参数
Table 6. State equation related parameters
表6. 状态方程相关参数
3.3. 爆破响应时程曲线获取
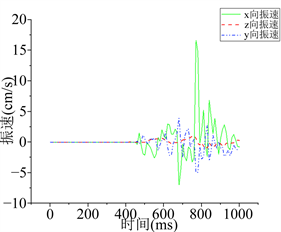(a) x、y、z各向速度时程曲线图 
(b) 三向合成速度时程曲线图
Figure 3. K0 + 500.70 m cross-section three-dimensional velocity time history curve
图3. K0 + 500.70 m横断面三向速度时程曲线图
图3所示为K0 + 500.70 m横断面工况下，分段延时爆破后洞室轮廓面所提取的三向速度时程曲线图。由图3可知，由于采用分段延时爆破，在雷管第15段(450 ms)起爆前，三向速度未产生较大波动，在雷管第15段起爆后，三向速度均产生了较大波动，随着后续分段爆破起爆产生的叠加效应，三向速度均逐渐增大，随着分段爆破全部完成，三向速度在达到峰值后逐渐减小趋于平衡。在爆破开始后768.41 ms处三向合成速度出现峰值，峰值速度为17.33 cm/s，其中三向速度中x向速度最大，x向峰值速度为16.58 cm/s。
4. 施工巷道单洞围岩动力响应分析
4.1. 计算模型建立
地下工程施工中，由于施工扰动的产生，岩层由地应力平衡状态发生应力释放，而应力释放区域大小为施工区域的3~5倍，因此在模拟中计算模型尺寸需为开挖区域的3倍及以上，即以开挖部分尺寸为基准，坐标原点选取洞口底部中心位置，模型x向为垂直隧道轴线水平方向，z向为竖直方向，y向为隧道进深方向，故本次模型在x、z方向分别延长3倍开挖洞室尺寸。本次施工巷道单洞模型高度取84 m，水平宽度取70 m，纵向进深取10 m。为了简化模型计算以及最大限度消除计算过程中不确定因素的影响，对地下水的影响不予考虑。
在爆破荷载输入时，将计算模型底部与前后左右边界设置为无反射边界，从而消除人为边界处的反射波对结构动力响应的影响。
4.2. 模拟爆破开挖过程
根据现场实际爆破开挖方案，采用全断面一步开挖，具体开挖过程如下：
(1) 第一步：对模型进行地应力平衡，模拟岩体在自然环境下稳定沉降，确保模型在进行爆破开挖前，自身处于平衡状态。
(2) 第二步：对洞室进行开挖，将第二章不同工况下所获取的三向振动速度时程曲线编写成离散元数值仿真软件中可识别的Table函数表，通过自编Fish函数，用Boundary命令将三向振动速度时程曲线输入在洞室开挖轮廓面的结点上，分析爆破扰动对洞室附近围岩的动力响应规律。
爆破动力输入节点示意图如图4所示。
Figure 4. Schematic diagram of blasting power input
图4. 爆破动力输入示意图
4.3. 围岩动力响应分析
图5所示为爆破载荷作用下施工巷道K0 + 500.70 m横断面围岩特征变量云图。爆破开挖后，施工巷道在地应力与爆破应力共同作用下，洞室顶部围岩整体产生竖向沉降，最大沉降量约为6.50 cm，出现在洞室顶板位置；施工巷道洞口处出现底板隆起，最大位移量约为2.39 cm；围岩总位移量最大值出现在洞室顶板及底板附近，最大总位移量约为6.51 cm。爆破开挖后，施工巷道洞室顶部与底板附近围岩呈拉主应力(图中所示拉应力为正，压应力为负)，最大拉应力值约为9.50 × 104 Pa，最大压主应力出现在洞室左右两侧直墙底角位置，最大压应力值约为9.42 × 105 Pa；洞室剪应变区域主要由洞室临空面向竖直方向发展，最大剪应变出现在洞室底板靠近直墙边处，最大剪应变增量约为1.49 × 10−2；围岩塑性区主要集中在洞室底板、顶部及两侧直墙处，洞室附近围岩体主要呈张拉破坏，洞室底板与直墙边交接处出现剪切破坏。洞室底板处相对于两侧边墙和洞顶处的塑性区影响范围略大，主要是因为在爆破开挖成洞的过程中，洞室顶部的拱形结构有着较好的承压能力，抵抗拱顶上方围岩自重与压力，而巷道洞室底部为平直结构，已形成应力集中，因此相对来说塑性区影响范围略大。
(a) x向峰值振速时程曲线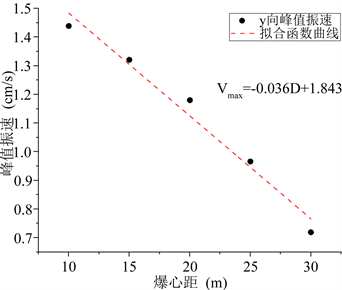 
(b) y向峰值振速时程曲线
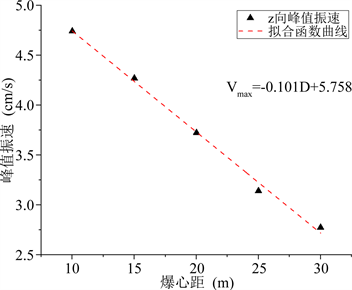(c) z向峰值振速时程曲线 
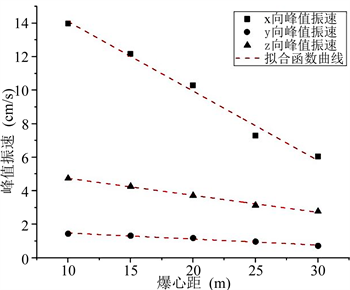(d) 三向峰值振速时程曲线
Figure 6. The three-way peak vibration velocity curves of different detonation center distances
图6. 不同爆心距的三向峰值振速曲线图
在对巷道洞室轮廓面施加爆破应力后，对围岩中各质点进行了振速时程监测，不同爆心距的三向峰值振速曲线如图6所示。其中三向振速峰值中最大值出现在x向，z向其次，y向最小，x向、y向、z向振速峰值最大值分别为14.0 cm/s、1.4 cm/s与4.7 cm/s；同时根据图中Vmax (峰值振速)与D (爆心距)线性拟合公式可知，随着爆心距的增加，振速峰值衰减幅度最大也出现在x向，x向振速峰值的衰减幅度分别为13.0%、26.4%、47.8%、56.3%，y向与z向振速峰值最大衰减幅度分别为50.0%和41.5%。
5. 结论
本文以某地下水封洞室施工巷道爆破施工为研究背景，结合项目工程地质条件与现场爆破方案，获取爆破动力时程曲线，研究依托工程施工巷道单洞围岩动力响应，并得出如下结论：
(1) 围岩塑性区主要集中在洞室底板、顶部及两侧直墙处，洞室附近围岩体主要呈张拉破坏，洞室底板与直墙边交接处出现剪切破坏。洞室底板处相对于两侧边墙和洞顶处的塑性区影响范围略大。
(2) 在对巷道洞室轮廓面施加爆破应力后，对围岩中的各质点进行了振速时程监测，单向最大振速峰值为x向，峰值为14.0 cm/s；同时振速峰值衰减幅度最大也出现在x向，随着爆心距的增加，x向振速峰值的衰减幅度分别为13.0%、26.4%、47.8%、56.3%。
基金项目
华东勘测设计研究院科技项目KY2021-ZX-09。