1. 引言
在1937年,意大利物理学家马约拉纳提出了一种新粒子,叫做马约拉纳费米子。马约拉纳费米子是一种特殊类型的费米子,其反粒子就是它本身 [1] 。马约拉纳零能模(MZM)也遵循描述马约拉纳费米子的马约拉纳方程,但它不是一种基本粒子,而是凝聚态物理中的准粒子。MZM具有三个基本特性:第一,它服从非阿贝尔统计,在量子计算中有着潜在的应用 [2] [3] 。其次,MZM具有非平庸的拓扑特性,它等价于拓扑超导体的边缘态,并且MZM的出现伴随着非平庸的全局拓扑不变量。第三,它具有粒子–空穴对称性,准粒子呈现电中性 [4] [5] [6] [7] 。由于MZM在物理学和量子计算机的应用中具有重要的意义,因此人们在实验中对MZM的寻找付出了巨大的努力。起初,人们意识到在手性p波超导体中可能有MZM的存在 [8] [9] [10] [11] [12] ,但手性p波超导体在实验上却很难实现 [13] 。在2008年,Fu和Kane提出在拓扑绝缘体和s波超导体的界面上可能存在MZM [14] 。Fu和Kane的工作启发了很多关于在实验中寻找MZM的研究 [15] 。近年来,人们研究了许多方案来寻找MZM,包括在金属Pb上嵌入一维Fe原子链和一维Rashba半导体线的实验 [16] [17] [18] [19] [20] 。已有实验在铁基超导体中发现了MZM [21] [22] [23] ,并且在铁基超导体中也报道了手性马约拉纳边缘模的存在 [24] 。由此可见铁基超导体具有很大的研究价值,这也是本文的主要出发点。
本文的其余部分组织如下:在第2节中,我们介绍了模型的8 × 8 Bogoliubov-de Gennes哈密顿量。在第3节中,我们介绍了该系统的拓扑相图 [25] ,并分析了系统最低束缚态能量与角动量的关系 [26] [27] 。在第4节中,我们求解了系统在拓扑平庸和非平庸情况下的零能量解。最后一节是结论部分。
2. 模型哈密顿量
我们采用Nambu基
来研究问题,这里的1和2是层指标,分别表示顶部和底部的表面状态,↑和↓分别表示自旋向上和自旋向下的伪自旋状态,
代表动量。在动量空间中,该系统的8 × 8 Bogoliubov-de Gennes哈密顿量如下所示:
(1)
(2)
(3)
这里的
表示Zeeman项,
表示化学势,t是底部和顶部表面态的耦合常数,
是表面内的自旋单态配对强度。
和
分别是表面间的自旋单态和自旋三重态配对强度。并且我们将费米速度
设成1。二维动量为
,这里的
和
以及
是Pauli矩阵,分别作用在自旋空间和表面空间以及粒子空穴空间。哈密顿量(1)式具有粒子空穴对称性,即:
,其中
,这里的
是作用在粒子空穴空间的Pauli矩阵,K代表复共轭算符。(1)式还具有转置对称性,即:
,其中
。当Zeeman项
时,(1)式还具有时间反演对称性,即:
,其中
,表示时间反演算符。除此之外,哈密顿量(1)式还有着关于xy平面的镜像对称性,即:
,其中
。
3. 拓扑相图和表面束缚态
3.1. 拓扑相图
对于正常态的哈密顿量
,同样有关于xy平面的镜像对称性
,即:
,并且满足:
,
(4)
镜像对称性
能被一般化为BdG哈密顿量形式,定义如下:
(5)
我们用下面的幺正变换来对角化
,
(6)
即:
(7)
哈密顿量(1)式变为:
(8)
当
时,哈密顿量(8)式可以块对角化为
,
(9)
(10)
拓扑相边界是由
点处的能隙所决定的,哈密顿量
和
在
点处的能隙分别如下:
(11)
(12)
其中
。当
,
时,我们得到的拓扑相图如下,
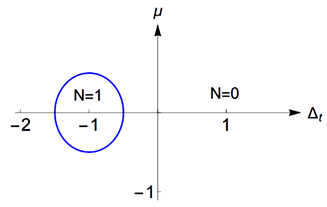 (a)
(a) 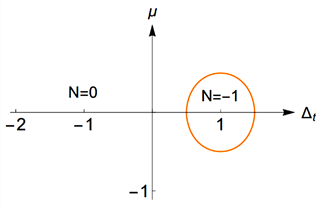 (b)
(b)
Figure 1. Topological phase diagrams of (a)
, (b)
in the
plane, we adopt this parameters:
,
,
,
图1.
和
的拓扑相图图(a),(b) 在
坐标系中,我们采用这些参数:
,
,
,
这里的N是陈数,当
时系统是拓扑平庸的,当
时系统是拓扑非平庸的。哈密顿量(1)的拓扑相图是
和
的相图之和,所以由图1可得到哈密顿量(1)的拓扑相图如下:

Figure 2. Topological phase diagrams of h in the
plane, we adopt this parameters:
,
,
,
图2. h的拓扑相图在
坐标系中,我们采用这些参数:
,
,
,
在接下来的讨论中,我们将利用图2来选取参数
和
。
3.2. 表面束缚态
在本章节中,我们将研究表面束缚态最低能量与角动量的关系。我们将在实空间中处理该问题,为
了计算方便我们将采用极坐标系
,配对项可以写成
,
,其中
是相干长度,在下面的计算中我们取
。动量算符
可以被写成:
,
(13)
并且满足:
(14)
(15)
上式的n取整数代表角动量,
是第一类Bessel函数。能量本征方程如下:
(16)
这里的
是哈密顿量(1)式在实空间的形式,本征态
其中
,
代表电子波函数,
代表空穴波函数,且都可以写成下列形式:
(17)
(18)
我们固定角动量n,然后在每个子空间去求解能量本征方程(16),将波函数分量
和
,(
)投影到半径为R的圆盘上,并用归一化的Bessel函数表示,那么
和
可以展开成下列形式:
(19)
(20)
这里的
,其中
是
的第k个零点,
和
是展开系数。通过这样做我们把求解能量本征方程(16)的问题变成了一个求解
的矩阵本征值问题,然后我们能得到能量本征值
,通过数值计算,最低本征能量
与角动量n的关系如下:
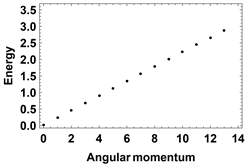 (a)
(a) 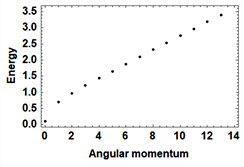 (b)
(b)
Figure 3. Numerical calculate results (a) and (b). (a) We adopted topological non-trivial parameters as:
,
,
,
,
,
. (b) We adopted topological trivial parameters as:
,
,
,
,
,
图3. 数值计算结果(a)和(b)。图(a)我们采用的是拓扑非平庸的参数:
,
,
,
,
,
。图(b)我们采用的是拓扑平庸的参数:
,
,
,
,
,
4. MZM
在图3(a)中我们注意到:当
时
,也就是说存在MZM。而图3(b)中,我们注意到:当
时
,即不存在MZM。为了更详细的讨论,接下来我们将求解波函数
和
。当
时,方程(16)可化为8个微分方程构成的方程组,我们采用数值求解计算来处理该问题,得到的波函数如下:
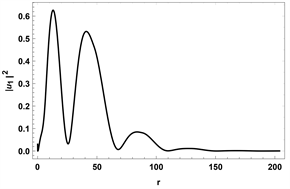 (a)
(a) 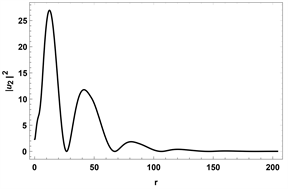 (b)
(b)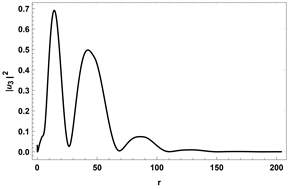 (c)
(c) 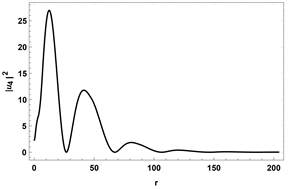 (d)
(d)
Figure 4. The wave function
,
,
,
, we adopted topological non-trivial parameters as:
,
,
,
,
,
. Note that all wave functions are not normalized. And
,
,
,
we can obtain by particle-hole symmetry
图4. 波函数
,
,
,
的图像,我们采用拓扑非平庸的参数:
,
,
,
,
,
。需要注意的是这里的波函数并未归一化,并且
,
,
,
我们可以通过粒子空穴对称性得到
 (a)
(a) 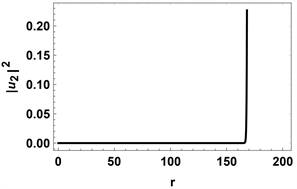 (b)
(b)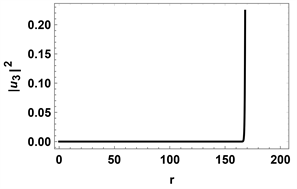 (c)
(c) 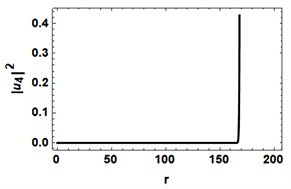 (d)
(d)
Figure 5. The wave function
,
,
,
, we adopted topological trivial parameters as:
,
,
,
,
,
. Note that all wave functions are not normalized. And
,
,
,
we can obtain by particle-hole symmetry
图5. 波函数
,
,
,
的图像,我们采用拓扑平庸的参数:
,
,
,
,
,
。需要注意的是这里的波函数并未归一化,并且
,
,
,
我们可以通过粒子空穴对称性得到
5. 结论
在本文中,我们研究了一个具有8 × 8 Bogoliubov-de Gennes 哈密顿量的系统,通过数值计算得到了最低束缚态能量与角动量的关系,并且我们还求解了零能态的波函数。由图3(a)和图4我们可以确定MZM存在于涡核附近,由图3(b)和图5我们可以确定在拓扑非平庸时,涡核附近不存在MZM,并且在远离涡核的地方波函数极度发散。因此,我们可以确定在拓扑非平庸的情况下,涡核附近存在MZM,平庸的情况则没有,并且最低束缚态能量与角动量成线性关系。