粒子群支持向量回归在金融时间序列预测中的应用

Application of Particle Swarm Support Vector Regression in Financial Time Series Prediction

摘要: 金融时间序列一直以来以其非线性、非平稳、信噪比低等特性成为时间序列预测中的难题。支持向量回归(SVR)在对时间序列进行预测时会有模型不稳定、预测精度不高等问题。上述问题的部分原因是模型中的参数选取可能会对预测结果造成影响，因此对于支持向量回归的参数选取问题给出粒子群支持向量回归模型(PSO-SVR)。该模型用粒子群优化算法代替传统的k折交叉验证法求出支持向量回归中的参数，再构建出PSO-SVR模型对金融时间序列进行预测。通过与传统k折交叉验证支持向量回归、BP神经网络以及随机森林模型(RF)预测后得到的均方误差、决定系数等比对，比对各项指标发现PSO-SVR模型要优于其余两者。鉴于PSO-SVR在稳定度和预测精度两方面的优势，表明该模型在金融时间序列的预测上有较好的体现。

Abstract: Financial time series has been a difficult problem in time series prediction with its non-linear, non-stationary and low signal to noise ratio. Support vector regression (SVR) has the problems of model instability and low prediction accuracy when predicting the time series. Part of the above problem is that the parameter selection in the model may affect the prediction results, so the par-ticle swarm support vector regression model (PSO-SVR) is given for the parameter selection problem of support vector regression. This model uses the particle swarm optimization algorithm instead of the traditional k-fold cross-validation method to find the parameters in the support vector regression, and then constructs the PSO-SVR model to predict the financial time series. The comparison shows that the PSO-SVR model is better with the traditional k-fold cross-validation support vector regression, BP neural network and random forest model (RF) prediction than the other two. Given the advantages of PSO-SVR in both stability and prediction accuracy, it shows that the model is well represented in the prediction of financial time series.

1. 引言

金融时间序列是时间序列的一种，对于金融时间序列的预测分为线性预测和非线性预测。近年来，非线性预测在预测领域逐渐代替线性预测成为主流，而支持向量回归(support vector regression, SVR)作为机器学习的非线性预测的主要方法，已被广泛应用于金融时间序列的研究中。彭丽芳等 [1] 利用SVM模型对股票价格进行了预测，取得了不错的实验结果。张伟 [2] 等提出了一种遗传算法(genetic algorithm, GA)与SVM相结合的方法，将其用来预测时间序列等。但上述文献对于SVM模型中的特征参数选取不够明确。本文利用粒子群算法(PSO)优化SVR模型参数，并将之用于金融时间序列预测中。李楠楠等 [3] 利用PSO-SVM模型对供水管网爆管位置和爆管程度的诊断准确程度是可以接受的。蔡正梓等 [4] 通过PSO-SVM模型实验得出该方法能有效识别变电站视频监控火灾。

本文先阐述该模型的构建理论 [5] ；再利用该模型对金融时间序列中的股票收盘价进行预测 [6] ，用取自东方财富网的A股东北制药、沪深300指数、美股道琼斯指数作实验数据，用MATLAB作实验程序；最后将预测结果以及误差指标与传统支持向量回归(SVR)、BP神经网络和随机森林(Random Forest, RF)的预测结果以及误差指标比对，突出了该模型对金融时间序列的预测能力。

2. 研究方法

2.1. SVR模型

支持向量回归(SVR)是支持向量机(SVM)的一个重要分支，其与SVM的不同在于SVM所追求的最优超平面是使得两类以及两类以上的样本点分得更开。而SVR的样本点最终只有一类，是使所有样本点距离超平面的偏差最小。由于金融时间序列通常是非线性的，给定训练样本集：

$S=\left\{\left(x_1,y_1\right),\cdots ,\left(x_l,y_l\right)\right\}\in {\left(X\times Y\right)}^l,X=R^n,Y=R$ (1)

训练样本集S是 $\epsilon$ -非线性近似的，若存在一个超平面：

$f\left(x\right)=\langle w,\varphi \left(x\right)\rangle +b,w\in R^n,b\in R$ (2)

下面的式子成立：

$\left|\langle w,\varphi \left(x_i\right)\rangle +b-y_i\right|\le \epsilon ,i=1,\cdots ,l$ (3)

考虑到误差的存在，所以引用松弛变量 $\xi ,{\xi }_i^{*}\ge 0,i=1,\cdots ,l$

优化方程为：

$\min \frac{1}{2}{\Vert w\Vert }^2+C{\displaystyle \underset{i=1}{\overset{1}{\sum }}\left({\xi }_i+{\xi }_i^{*}\right)}$ (4)

约束为

$\langle w,\varphi \left(x_i\right)\rangle +b-y_i\le {\xi }_i^{*}+\epsilon ,i=1,\cdots ,l$ (5)

$y_i-\langle w,\varphi \left(x_i\right)\rangle -b\le {\xi }_i+\epsilon ,i=1,\cdots ,l$ (6)

${\xi }_i,{\xi }_i^{*}\ge 0,i=1,\cdots ,l$ (7)

其中 $\frac{1}{2}{\Vert w\Vert }^2$ 使函数更为平坦，进而提高泛化能力。C为惩罚系数，即对误差的容忍度，C越大，说明越不

能容忍出现误差，容易过拟合；C越小，说明模型对于误差比较宽容，但容易欠拟合。对上述优化问题引用拉格朗日函数并写出对偶形式：

$\underset{\alpha ,{\alpha }^{*}}{\text{max}}-\frac{1}{2}{\displaystyle \underset{i,j=1}{\overset{l}{\sum }}\left({\alpha }_i-{\alpha }_i^{*}\right)\left({\alpha }_j-{\alpha }_j^{*}\right)K\left(x_i,x_j\right)+{\displaystyle \underset{i=1}{\overset{l}{\sum }}\left({\alpha }_i-{\alpha }_i^{*}\right)y_i-{\displaystyle \underset{i=1}{\overset{l}{\sum }}\left({\alpha }_i+{\alpha }_i^{*}\right)\epsilon }}}$ (8)

约束为：

${\displaystyle \underset{i=1}{\overset{l}{\sum }}\left({\alpha }_i-{\alpha }_i^{*}\right)=0}$ (9)

$0\le {\alpha }_i,{\alpha }_i^{*}\le C,i=1,\cdots ,l$ (10)

其中 ${\alpha }_i,{\alpha }_i^{*}$ 为拉格朗日算子， $f\left(x\right)$ 的表达式为：

$f\left(x\right)={\displaystyle \underset{i=1}{\overset{l}{\sum }}\left(a_i-a_i^{*}\right)K\left(x_i,x\right)+b}$ (11)

其中核函数 $K\left(x_i,x\right)$ 用来代替内积 $\langle \varphi \left(x_i\right),\varphi \left(x\right)\rangle$ ， $w={\displaystyle \underset{i=1}{\overset{l}{\sum }}\left({\alpha }_i-{\alpha }_i^{*}\right)\varphi \left(x_i\right)}$ ，核函数取高斯径向基核函数：

$K\left(x_i,x\right)=\text{exp}\left(-\frac{d{\Vert x-x_i\Vert }^2}{2{\sigma }^2}\right)=\text{exp}\left(-\gamma {\Vert x-x_i\Vert }^2\right)$ (12)

其中 $\gamma$ 作为参数，决定了数据映射到特征空间的分布， $\gamma$ 越大，支持向量越少， $\gamma$ 越小，支持向量越多，支持向量的个数影响着训练与预测的速度。在SVR中，选择合适的参数C和 $\gamma$ 尤为重要。

2.2. PSO算法

粒子群优化算法(Particle Swarm Optimization)是通过模拟鸟类觅食过程中的行为演化而得到的一种群体智能算法。假设鸟类群体觅食，每只鸟都共享有食物的位置的信息，寻找的过程中不断记录并依据信息更新自己的飞行方向，最后找到一个食物最多的位置。类比鸟类群体觅食，把鸟看成粒子，把食物的量看成目标函数值(适应度函数值)，每只鸟所处的位置看作空间中的一个解，食物量最多的位置看成全局最优解。

假设在D维搜索空间中，有N个粒子，粒子有两个重要属性：速度和位置，速度表示粒子下一步迭代时移动的方向和距离，位置是所求解问题的一个解。则有如下速度更新公式：

$v_{id}^{k+1}=\omega v_{id}^k+c_1{r}_1\left(p_{id,pbest}^k-x_{id}^k\right)+c_2{r}_2\left(p_{d,gbest}^k-x_{id}^k\right),i=1,\cdots ,N;d=1,\cdots ,D$ (13)

位置公式：

$x_{id}^{k+1}=x_{id}^k+v_{id}^{k+1},i=1,\cdots ,N;d=1,\cdots ,D$ (14)

公式(13)中第一项为惯性部分，第二项为自我认知部分，第三项为群体信息部分。k为迭代次数； $\omega$ 为惯性权重； $c_1,c_2$ 分别为个体与群体学习因子； $r_1,r_2$ 为区间 $\left[0,1\right]$ 内的随机数，增加搜索的随机性； $v_{id}^k$ 为粒子i在第k次迭代中第d维的速度向量； $x_{id}^k$ 为粒子i在第k次迭代中第d维的位置向量； $p_{id,pbest}^k$ 为第i个粒子在第k次迭代中第d维的最优位置，即个体最优解； $p_{d,gbest}^k$ 为群体在第k次迭代中第d维的最优位置，即群体最优解；以及能够计算出的个体最优适应值 $f_p$ 与群体最优适应值 $f_g$ 。

3. PSO-SVR模型

对于上文所提到的SVR模型中的参数C与 $\gamma$ ，二者会影响SVR预测模型的精度。先用PSO优化算法去得到最优参数C与 $\gamma$ ，再带入到SVR中就会提高模型的精度。给出如下步骤，如图1所示：

Figure 1. Flow-process diagram

图1. 流程图

1) 确定样本数据，输入粒子群规模N,粒子维度D，惯性权重 $\omega$ ，学习因子 $c_1,c_2$ ，最大迭代次数。

2) 初始化个体的位置 $x_{id}^0$ 与速度 $v_{id}^0$ ，并计算出初始个体与群体适应度函数值。

3) 运用公式(13)与公式(14)更新每个粒子的速度和位置并计算个体与群体适应度函数值，选出历史最优适应度函数值。

4) 判断是否满足迭代终止条件，若不满足，返回步骤3)。

5) 若满足，输出最优解。把输出的最优解作为SVR模型的参数进行建模。

6) 用步骤5)优化后的SVR模型进行预测回归。

4. 实证研究

4.1. 数据来源

选取来源于东方财富网的A股东北制药2022年1月至2022年12月、沪深300指数2021年1月至2022年12月、美股道琼斯指数1月至2022年12月的收盘价作为实验数据。用前三期收盘价作为输入，第四期收盘价作为输出训练模型。取前4/5为训练集，取后1/5为测试集。

4.2. 评价指标

本文采用平均绝对误差(MAE)、均方误差(MSE)、平均绝对百分比误差(MAPE)、决定系数(R方)、测试时间作为模型评价指标。

$\text{MAE}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|f\left(x_i\right)-y_i\right|}$ (15)

$\text{MSE}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(f\left(x_i\right)-y_i\right)}^2}$ (16)

$\text{MAPE}=\frac{100\%}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|\frac{f\left(x_i\right)-y_i}{y_i}\right|}$ (17)

${\text{R}}^2=1-\frac{{\displaystyle \underset{i}{\sum }{\left(f\left(x_i\right)-y_i\right)}^2}}{{\displaystyle \underset{i}{\sum }{\left({\bar{y}}_i-y_i\right)}^2}}$ (18)

4.3. 实验结果与分析

对数据进行归一化处理后采用粒子群优化算法来优化SVR中的参数C与 $\gamma$ ，这里由于只需要优化两个参数，所以粒子群维数 $D=2$ ，取学习因子 $c_1=c_2=1.5$ ，粒子群规模 $N=20$ ，最大迭代次数为100，将数据带入到PSO模型后得到适应度曲线如图2所示，最优参数如表1所示。

利用上述得到的最优参数对SVR进行建模得到PSO-SVR模型。用传统k折交叉验证求得的SVR模型、BP神经网络以及RF模型与本文模型进行实验比对，评价指标比对结果如表2所示，预测结果如图3所示，残差如图4所示。

Table 1. Optimal parameters for the different experimental data

表1. 不同实验数据最优参数

Figure 2. Fitness curve

图2. 适应度曲线

Table 2. Comparison diagram of the evaluation indicators of the different models

表2. 不同模型评价指标对比图

由表2可以看出相比于SVR，PSO-SVR不仅各项评价指标要优于前者，而且能大大缩短测试时间；本文模型除了测试时间，其余各项指标均优于BP神经网络与RF模型。

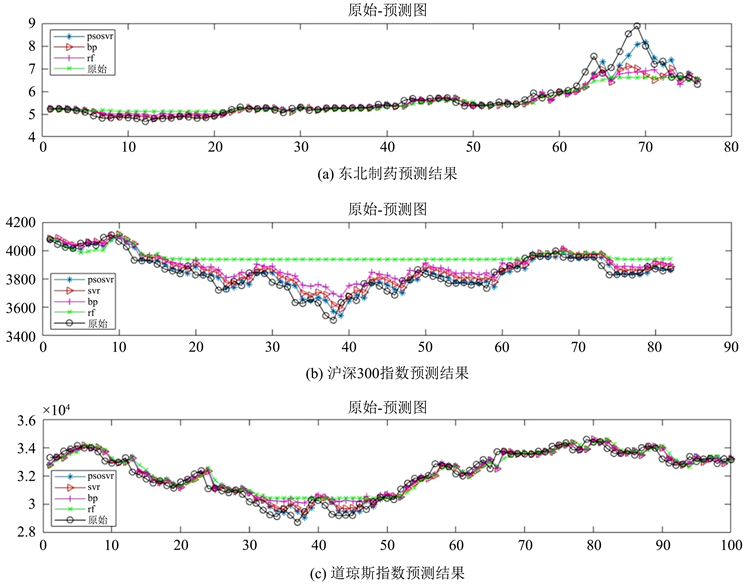
Figure 3. Comparison of the prediction results of the different models

图3. 不同模型预测结果对比

由图3可以观测出，对于平稳金融时间序列而言，四种模型的预测能力都令人满意，但在东北制药第60个测试数据之后、沪深300指数第10至第65个测试数据之间以及道琼斯指数第30至第50个测试数据之间，四种模型都有不同程度的预测误差，但也能看出PSO-SVR模型误差最小，其次是SVR模型和BP神经网络，最后是RF模型。模型精度还不够高的原因可能有：1) 实验中使用的金融时间序列的特征指标有限，仅仅使用了实验数据的收盘价。2) 实验中使用的金融时间序列的数据的范围有限，对预测的数据有一定影响。3) 实验中使用的金融时间序列没有考虑到政策、疫情等因素对股票收盘价的影响。结合图4也能发现，虽然在三组数据中的某一部分都有四种模型的误差整体偏大的情况，但能明显观测出PSO-SVR的残差点的分布更为紧凑，可以认为该模型比较有效。

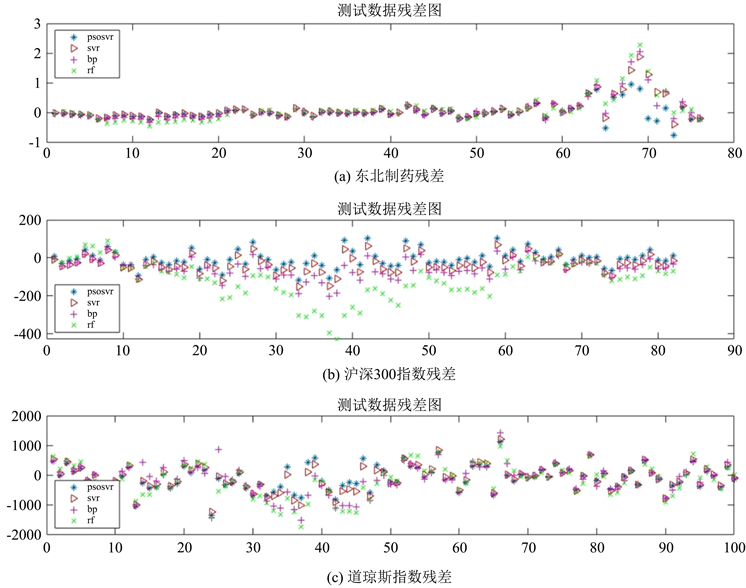
Figure 4. Comparison of residuals for different models

图4. 不同模型残差对比

5. 结果与展望

粒子群优化算法支持向量回归模型包含着PSO算法中参数少、计算快以及SVR模型学习能力强、学习速度快的优点，更重要的是PSO算法能提高SVR模型的精度。

不足之处在于该模型的实验中只是选取了前几期的收盘价作为输入，若取前期的开盘价、最高价、KJD等指标作为输入，也许会有不同的效果。所以在该模型的基础上，可从特征选取、特征降维等方面进行加深实验研究。

总之采用该模型对金融时间序列进行预测，有着减少误差降低风险的效果，仍具有良好的应用前景。

基金项目

项目名称：深度学习在数据分析中的应用研究。

项目类别：省教育厅项目。

项目批号：LJKMZ20221424。