摘要: 本文研究半正二阶问题
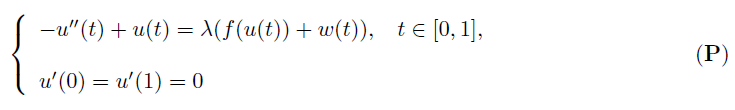
正解的存在性,其中 λ 为正参数,w∈C([0,1], ℝ) 满足 |w(t)| ≤ c, t ∈ [0, 1], c 为任意正常数,
f ∈ C([0, ∞), [0, ∞)),且满足超线性条件,即
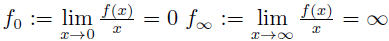
。通过运用锥上的不动点定理证明了存在常数 λ
0 > 0,当 0 < λ < λ
0 时,问题 (P) 存在一个正解。
Abstract:
We are concerned with existence of positive solutions of semi-positone second order problems
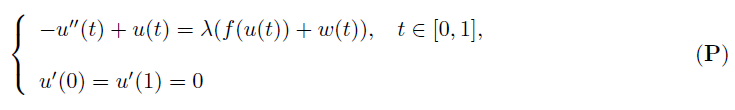
where λ is a positive parameter, w∈C([0,1], ℝ), and |w(t)| ≤ c, t ∈ [0, 1],c is a positive constant, f ∈ C([0, ∞), [0, ∞)), and f is superlinear, i.e,
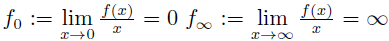
. By using fixed point theorem in cones, we show that there exists a constant λ
0 > 0 such that (P) has a positive solution for 0 < λ < λ
0.