脉冲切换系统有限时间输入到状态稳定性研究

Study on Finite-Time Input-to-State Stability of Impulsive Switched Systems

摘要: 我们将有限时间输入到状态稳定性(FTISS)的分析扩展到脉冲切换系统。给出了基于李雅普诺夫理论和固定驻留时间条件下的有限时间输入到状态稳定性的充分条件。本文的结果还包括脉冲频率、系统结构和外部输入的关系，以保证脉冲切换系统的有限时间输入到状态稳定性。在有限时间框架下，研究表明，满足有限时间输入到状态稳定性的系统的运动轨迹将在有限时间内进入最终界限，此后不会超过这一界限。并通过实例说明了该理论的正确性。

Abstract: We extend the analysis of finite-time input-to-state stability to impulsive switched systems. Based on Lyapunov theory and fixed residence time, a sufficient condition for the stability of finite-time input-to-state is given. The results of this paper also include the relationship between pulse fre-quency, system structure and external input to ensure the finite-time input-to-state stability of pulse switched systems. In the finite-time frame, it is shown that the trajectory of the system with finite-time input-to-state stability will enter the final limit in a finite time, and will not exceed the limit thereafter. The correctness of the theory is illustrated by an example.

1. 引言

切换系统是一类重要的混杂动力系统。它由两部分组成：微分方程或差分方程描述的一系列子系统和控制它们之间切换的切换信号。在切换系统中，我们通常称每一个子系统为一种模式。切换系统可以用来模拟许多现象，而这些现象不能用纯粹的连续或纯粹的离散过程来描述。例如生物系统 [1] ，具有不同齿轮的汽车和机车 [2] ，制造工艺 [3] 等。所以切换系统在具体生活和研究中是不可忽视的，在近些年中，许多学者在切换系统的分析和研究方面付出了相当大的努力。切换系统的一个基本研究问题是稳定性。由于切换系统的混合特性，很难单独处理与连续时间系统或离散时间系统的比较，因此成为一个具有挑战性的任务。对于任意切换下的稳定性，所有子系统都需要公共李亚普诺夫函数 [4] 。依赖于时间的切换系统，驻留时间和平均驻留时间方法已被用来研究稳定性和稳定性问题 [5] [6] 。混杂系统的另一个重要类型是脉冲系统，它由三部分组成：一个连续的过程，它控制着系统在脉冲之间的连续演化；一个离散的过程，它控制着系统状态突然改变脉冲时间的方式；以及一个脉冲定律，它决定着脉冲发生的时间。关于脉冲系统的早期工作可以在 [7] 中找到。这些工作已经成功地建立了一个具有形式定义和初始假设的脉冲系统的理论。因此，关于脉冲系统方面的理论研究和具体应用具有很重要的现实意义，已经成为控制理论方面和数学等领域中许多学者十分感兴趣的一个研究课题。另一方面，现实世界中的一些切换系统，如经济学中的最优控制模型，调频信号处理系统，病理学中的突发节奏模型和飞行物体运动，在切换点显示出某种具有脉冲效应的动力学 [8] [9] 。这些类型的切换系统对应于一个更加全面的模型，即所谓的脉冲切换系统，它不能很好地用纯粹连续或纯粹离散的模型来描述。在过去的十年中，脉冲切换系统已经得到了相当多的关注 [10] 。

迄今为止，大多数关于切换系统稳定性的结果都与李雅普诺夫渐近稳定性或指数稳定有关，这种稳定性定义在一个无限时间区间内。然而，在许多实际情况下，我们感兴趣的是系统在固定的有限时间间隔内的稳定性。这种稳定性称为有限时间稳定性(FTS)。如果系统的状态在一个固定的时间间隔内没有超过规定的区域，那么系统就是有限时间稳定的。应该明确指出，有限时间稳定性和李雅普诺夫渐近稳定性是两个独立的概念：一个有限时间稳定的系统可能不是李雅普诺夫渐近稳定的，反之亦然。近年来，许多学者对切换系统的有限时间稳定性进行了研究。在 [11] 中，研究了一类具有时变外部扰动的切换线性系统的有限时间有界性和镇定问题。基于线性矩阵不等式(LMI)，给出了切换线性系统有限时间有界和一致有限时间有界的一些充分条件。然而，在切换点的脉冲效应没有被考虑。正如我们所知，许多进化过程，特别是一些生物系统，是拥有属性状态的转换和转换瞬间的突然变化。因此，我们有必要去对脉冲切换系统方面进行研究。对于脉冲系统的有限时间稳定性，一些结果已经在 [12] 中研究。在输入系统中，输入到状态稳定(ISS)描述了外部输入对系统稳定性的影响，除了作为分析工具之外，在非线性控制系统的设计中具有核心作用，使其在过去几年也引起了许多关注 [13] 。除了作为分析工具之外，ISS理论在非线性控制系统的设计中具有核心作用，特别是在非线性系统的鲁棒镇定，跟踪设计，非线性系统的小增益定理和非线性观测器的设计中 [14] [15] 。文献 [16] 中首次引入了FTISS，并提出了非线性系统FTISS的几个充分条件和必要条件。文献 [17] 利用平均驻留时间方法，结合代数矩阵理论讨论了具有脉冲效应的扰动切换系统的有限时间稳定性问题。文献 [18] 通过李雅普诺夫方法和平均驻留时间方法研究了脉冲切换系统的输入输出到状态稳定。

基于上述工作和实际背景，本文对于实际系统来说，扰动和脉冲效应是不可避免的，它们会降低系统的性能甚至使系统失稳。因此，研究这些系统的稳定性是非常有意义和迫切的。据我们所知，对于脉冲切换系统的有限时间输入到状态稳定这个问题还没有得到探索，这也激发了我们的研究。文献 [19] 利用李雅普诺夫理论和驻留时间法给出了非线性脉冲系统FTISS的充分条件，具体地说，存在具有局部Lipschitz连续函数 $V:{ℝ}^n\to {ℝ}_{+}$ 使得

$D^{+}V\left(x\left(t\right)\right)\le -c{V}^{\alpha }\left(x\left(t\right)\right)$ ，当 $V\left(x\left(t\right)\right)\ge \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$ ，

其中 $c>0$ ， $\alpha \in \left(0,1\right)$ ， $\omega$ 为外部输入。但是，现实中很多问题仅仅通过非线性脉冲系统建模很难准确研究和解决相应的问题。所以本节将其推广到脉冲切换系统中。即存在具有局部Lipschitz连续函数 $V_i:{ℝ}^n\to {ℝ}_{+}$ 使得

$D^{+}{V}_i{\left[x\left(t\right)\right]}_f\le -c{V}_i{}^{\alpha }\left(x\left(t\right)\right)$ ，当 $V_i\left(x\left(t\right)\right)\ge \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$ 。

本文的目的是研究脉冲切换系统的有限时间输入到状态稳定性，基于李雅普诺夫理论和固定驻留时间方法，得到了与脉冲频率、系统结构和外部输入有关的脉冲切换时间序列。在子系统都是稳定且脉冲不稳定的情况下，满足这样的脉冲切换时间序列，我们可以得到有限时间输入到状态稳定的结论。本文的其余部分组织如下：在第二节中介绍了一些预备知识，在第三节中给出了脉冲切换系统有限时间输入到状态稳定的充分条件，在第四节中给出了实例来证明其有效性。

2. 预备知识

令 $ℝ$ 为实数集； ${ℝ}_{+}$ 为非负实数集； $\mathbb{N}$ 为正整数集； ${\mathbb{Z}}_0$ 为非负整数集； ${ℝ}^n$ 为n维欧氏空间； $\left|\cdot \right|$ 为二维欧氏范数； $a\vee b$ 和 $a\wedge b$ 分别为a和b的最大值和最小值；对于 $I\subseteq ℝ$ ， $m\ge 1$ ，令 $\omega :I\to {ℝ}^m$ 是一个可测的基本有界函数且 ${\Vert \omega \Vert }_I:=\sup \left\{\left|\omega \left(t\right)\right|:t\in I\right\}$ 为最大范数，特别地 ${\Vert \omega \Vert }_{\infty }:={\Vert \omega \Vert }_{[0,\infty )}$ ，对于 $\rho >0$ ， $U_{\rho }:=\left\{x\in {ℝ}^n|\left|x\right|<\rho \right\}$ 。

考虑下列脉冲切换系统

$\{\begin{array}{l}\stackrel{\dot{}}{x}=f_{\sigma \left(t\right)}\left(x,\omega \right),t\ne t_n,n\in {\mathbb{Z}}_{+},\\ x\left(t\right)=g_{\sigma \left(t^{+}\right)}\left(x\left(t^{-}\right)\right),t=t_n,n\in {\mathbb{Z}}_{+},\end{array}$ (1)

这里 $x\left(t\right)\in {ℝ}^n$ 为系统状态； $\omega \left(t\right)\in {ℝ}^m$ 是一个可测的基本有界的外部输入； $\sigma \left(t\right):[0,\infty )\to S\triangleq \left\{1,2,\cdots ,r,r+1,\cdots ,l\right\}$ 是一个确定的右连续的分段常数函数，l是子系统的个数；切换序列可以表示为 $\sigma :\left\{\left(t_0,\sigma \left(t_0\right)\right),\left(t_1,\sigma \left(t_1\right)\right),\cdots ,\left(t_k,\sigma \left(t_k\right)\right),\cdots \right\}$ ，当 $t\in [t_k,t_{k+1})$ 时，则 $\sigma \left(t_k\right)$ 子系统激活。 $f:{ℝ}^n\times {ℝ}^m\to {ℝ}^n$ 和 $g:{ℝ}^n\times {ℝ}^m\to {ℝ}^n$ 是满足 $f\left(0,0\right)=g\left(0,0\right)=0$ 的连续函数；脉冲时间序列 ${\left\{t_k\right\}}_{k\in \mathbb{N}}$ 满足 $0:=t_0<t_1<\cdots <t_k<\cdots$ 且 ${\lim }_{k\to +\infty }{t}_k=+\infty$ ；假设函数f满足适当的条件使得解 $x\left(t\right)=x\left(t,x_0\right)$ 在相关时间间隔内存在唯一正向解；假设 $x\left(t\right)$ 和 $\omega \left(t\right)$ 是左连续；对于给出的脉冲时间序列 $\left\{t_k\right\}$ ， $N\left(t,s\right)$ 表示系统(1)在半开区间 $(s,t]$ 上的脉冲次数。

给定一个局部Lipschitz连续函数 $V_i:{ℝ}^n\to {ℝ}_{+}$ ， $i\in S$ ，定义了 $V_i$ 关于系统(1)的第i个右上导数为

$D^{+}{V}_i{\left[x\left(t\right)\right]}_f=\lim {\sup }_{h\to 0^{+}}\frac{1}{h}\left(V_i\left(x\left(t\right)+h{f}_i\left(x\left(t\right),\omega \left(t\right)\right)\right)-V_i\left(x\left(t\right)\right)\right)$ .

定义1.1 [19] ：如果函数 $\gamma :{ℝ}_{+}\to {ℝ}_{+}$ 是连续的，严格递增并且 $\gamma \left(0\right)=0$ ，则称函数 $\gamma$ 是 $\mathcal{K}$ 类函数。如果函数 $\gamma \in \mathcal{K}$ 也是无界的，则称函数 $\gamma$ 是 ${\mathcal{K}}_{\infty }$ 类函数。

定义1.2 [19] ：如果函数 $\beta :{ℝ}_{+}\times {ℝ}_{+}\to {ℝ}_{+}$ 满足：

(i) 对每一个固定 $t\ge 0$ ， $\beta \left(\cdot ,t\right)$ 关于第一个变量是 $\mathcal{K}$ 类函数；

(ii) 对于每一个固定 $s\ge 0$ ，且当 $t\to \infty$ 时， $\beta \left(s,t\right)$ 递减趋于0；

则称 $\beta$ 是 $\mathcal{K}\mathcal{L}$ 类函数。

定义1.3 [19] ：如果函数 $\beta :{ℝ}_{+}\times {ℝ}_{+}\to {ℝ}_{+}$ 满足：

(i) 对于每一个固定 $s\ge 0$ ，存在 $T\left(s\right)<\infty$ ，使得当 $t\to T\left(s\right)$ 时， $\beta \left(s,t\right)$ 递减趋于0；

(ii) $\beta \left(0,0\right)=0$ ；

(iii) 对于每一个固定 $t\ge 0$ 有

$\{\begin{array}{l}\beta \left(s_1,t\right)>\beta \left(s_2,t\right),\text{if}\beta \left(s_1,t\right)>0,s_1>s_2,\\ \beta \left(s_1,t\right)=\beta \left(s_2,t\right),\text{if}\beta \left(s_1,t\right)=0,s_1>s_2,\end{array}$

则称函数 $\beta :{ℝ}_{+}\times {ℝ}_{+}\to {ℝ}_{+}$ 是 $\mathcal{K}{\mathcal{L}}_0$ 类函数。

定义1.4：设 $U\subseteq {ℝ}^n$ 是一个包含原点的开集，如果存在 $\beta \in \mathcal{K}{\mathcal{L}}_0$ ， $\gamma \in {\mathcal{K}}_{\infty }$ 使得对任意 $x_0\in U$ 和 $\omega \left(t\right)\in {ℝ}^m$ ，系统(1)的解 $x\left(t,x_0\right)$ 满足

$\left|x\left(t,x_0\right)\right|\le \beta \left(\left|x_0\right|,t\right)+\gamma \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$ ，对 $\forall t\ge 0$ ， (2)

则系统(1)是FTISS。

与传统的ISS相比，FTISS的主要区别在于对于给定的初始状态 $x_0\in {ℝ}^n$ ， $x\left(t,x_0\right)$ 将在有限时间内进入最终界限，并且此后不超过这个界限。

假设 $\mathcal{F}$ 表示一类可容许的脉冲时间序列， ${\mathcal{F}}_{\tau }$ 表示一类满足固定驻留时间(FDT)条件的脉冲时间序列，即 ${\inf }_{k\in {\mathbb{Z}}_0}\left\{t_{k+1}-t_k\right\}\ge \tau$ ， $\forall \left\{t_k\right\}\in {\mathcal{F}}_{\tau }$ 。

3. 主要结果

定理2.1：假设 $V_i:{ℝ}^n\to {ℝ}_{+}$ 是一个局部Lipschitz连续函数，如果存在函数 ${\phi }_1,{\phi }_2,\chi \in {\mathcal{K}}_{\infty }$ ，常数 $c>0$ ， $\alpha \in \left(0,1\right)$ ， $\mu \ge 1$ ， $\vartheta >0$ ，使得：

(A₁) ${\phi }_1\left(\left|x\right|\right)\le V_i\left(x\right)\le {\phi }_2\left(\left|x\right|\right)$ ， $x\in {ℝ}^n$ ；

(A₂) $V_i\left(x\left(t_k\right)\right)\le \mu V_j\left(x\left(t_k^{-}\right)\right)$ ， $x\in {ℝ}^n$ ， $\forall \left(\sigma \left(t_k\right)=i,\sigma \left(t_k^{-}\right)=j\right)\in S\times S$ ， $i\ne j$ ；

(A₃) 当 $V_i\left(x\left(t\right)\right)\ge \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$ 时：

$D^{+}{V}_i{\left[x\left(t\right)\right]}_f\le -c{V}_i{}^{\alpha }\left(x\left(t\right)\right)$ , $t\ne t_k$ , (3)

其中 $x\left(t\right)$ 为系统(1)初值为 $x\left(0\right)=x_0$ 的解，这里 $x_0\in U_{\vartheta }$ ；

(A₄) $c\left(1-\alpha \right)\tau >\left(1-\frac{1}{{\mu }^{1-\alpha }}\right){\psi }^{1-\alpha }\left(\vartheta \right)$ ，

这里 $\psi \left(\vartheta \right):=\left({\phi }_2\left({\phi }_1^{-1}\left(\mu {\phi }_2\chi \left({\Vert \omega \Vert }_{\infty }\right)\right)\right)\right)\vee {\phi }_2\left(\vartheta \right)$ ，则系统(1)在 ${\mathcal{F}}_{\tau }$ 上是FTISS。

证明：对于任意满足条件(A₄)的 $\tau >0$ ，可以找到一个充分小的常数 $\delta >0$ 使得

$c\left(1-\alpha \right)\tau \ge \left(1-\frac{1}{{\mu }^{1-\alpha }}\right){\psi }^{1-\alpha }\left(\vartheta \right)+\delta$ 。特别地， $c\left(1-\alpha \right)\tau \ge \delta$ (4)

令 $\left\{t_k\right\}\in {\mathcal{F}}_{\tau }$ 为任意脉冲时间序列。假设 $x\left(t\right)=x\left(t,x_0\right)$ 是系统(1)以 $x\left(0\right)=x_0$ 为初值的解，这里 $x_0\in U_{\vartheta }$ 。为了方便，我们令 ${\nu }_i\left(t\right):=V_i\left(x\left(t\right)\right)$ 。对于任意 $s\ge 0$ ，定义：

${\beta }_1\left(s,t\right):={\psi }^{1-\alpha }\left(s\right)-k\delta -\frac{t-t_k}{t_{k+1}-t_k}\delta$

这里 $t\in [t_k,t_{k+1})$ 且 $k\in {\mathbb{Z}}_0$ 。定义

${\beta }_2\left(s,t\right):=\{\begin{array}{ll}{\beta }_1^{\frac{1}{1-\alpha }}\left(s,t\right),\hfill & t\in [0,T\left(s\right)),\hfill \\ 0,\hfill & t\ge T\left(s\right),\hfill \end{array}$

这里 $T\left(s\right):=\inf \left\{t\ge 0|{\beta }_1\left(s,t\right)\le 0\right\}$ 。下面证明

${\nu }_{\sigma \left(t\right)}\left(t\right)\le {\beta }_2\left(\left|x_0\right|,t\right)\vee \chi \left({\Vert \omega \Vert }_{\infty }\right)$ ，对 $\forall t\ge 0$ 。 (5)

因为 $x\left(t\right)$ 和 $\omega \left(t\right)$ 在脉冲点上右连续，所以存在一个时间序列 $0:=t_0^{\vee }\le t_1^{\wedge }<t_1^{\vee }<t_2^{\wedge }<t_2^{\vee }<\cdots$ 使得对于 $l\in {\mathbb{Z}}_0$ 有

${\nu }_{\sigma \left(t\right)}\left(t\right)\ge \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$ , $\forall t\in \left[t_{l-1}^{\vee },t_l^{\wedge }\right)$ , (6a)

${\nu }_{\sigma \left(t\right)}\left(t\right)\le \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$ , $\forall t\in \left[t_l^{\wedge },t_l^{\vee }\right)$ .(6b)

定义在区间 $\left[t_{l-1}^{\vee },t_l^{\wedge }\right)$ 上的脉冲点为 $t_{{\xi }_l+1},\cdots ,t_{{\xi }_l+N\left(t_l^{\wedge },t_{l-1}^{\vee }\right)}$ ，这里 ${\xi }_l=N\left(t_{l-1}^{\vee },t_0^{\vee }\right)$ 。

为此，我们首先将区间 $[0,\infty )$ 分解为子区间的并。

下面我们分两种情况考虑：情况(i) $t_1^{\wedge }>0$ ，即 $\left[0,t_1^{\wedge }\right)\ne \varnothing$ ；情况(ii) $t_1^{\wedge }=0$ ，即 $\left[0,t_1^{\wedge }\right)=\varnothing$ 。若情况(i)成立，对于 $\forall t\in \left[0,t_1^{\wedge }\right)$ ，当 $N\left(t_1^{\wedge },0\right)=0$ 时，即在区间 $\left[0,t_1^{\wedge }\right)$ 上没有脉冲，由(A₁)、(3)和(4)得

$\begin{array}{c}{\nu }_{\sigma \left(t_0\right)}^{1-\alpha }\left(t\right)\le {\nu }_{\sigma \left(t_0\right)}^{1-\alpha }\left(t_0\right)-c\left(1-\alpha \right)\left(t-t_0\right)\\ \le {\phi }_2^{1-\alpha }\left(\left|x_0\right|\right)-c\left(1-\alpha \right)\left(t-t_0\right)\\ \le {\phi }_2^{1-\alpha }\left(\left|x_0\right|\right)-\frac{t-t_0}{t_1-t_0}\delta .\end{array}$ (7)

当 $N\left(t_1^{\wedge },0\right)>0$ 时，在区间 $\left[0,t_1^{\wedge }\right)$ 上的脉冲点为 $t_{{\xi }_1+i}=t_i$ ， $i\in \left\{1,\cdots ,N\left(t_1^{\wedge },0\right)\right\}$ 。所以由(6)得

${\nu }_{\sigma \left(t_0\right)}^{1-\alpha }\left(t\right)\le {\phi }_2^{1-\alpha }\left(\left|x_0\right|\right)-\frac{t-t_0}{t_1-t_0}\delta$ , $t\in [t_0,t_1)$ .

当 $t\in \left[t_1,t_2\wedge t_1^{\wedge }\right)$ 时，结合(4)和(7)得

$\begin{array}{c}{\nu }_{\sigma \left(t_1\right)}^{1-\alpha }\left(t\right)\le {\nu }_{\sigma \left(t_1\right)}^{1-\alpha }\left(t_1\right)-c\left(1-\alpha \right)\left(t-t_1\right)\\ \le {\mu }^{1-\alpha }{\nu }_{\sigma \left(t_0\right)}^{1-\alpha }\left(t_1^{-}\right)-c\left(1-\alpha \right)\left(t-t_1\right)\\ \le {\mu }^{1-\alpha }\left({\phi }_2^{1-\alpha }\left(\left|x_0\right|\right)-c\left(1-\alpha \right)\left(t_1-t_0\right)\right)-c\left(1-\alpha \right)\left(t-t_1\right)\\ \le {\mu }^{1-\alpha }\left({\phi }_2^{1-\alpha }\left(\left|x_0\right|\right)-c\left(1-\alpha \right)\tau \right)-c\left(1-\alpha \right)\left(t-t_1\right)\end{array}$

$\begin{array}{l}\le {\mu }^{1-\alpha }\left({\phi }_2^{1-\alpha }\left(\left|x_0\right|\right)-\left(1-\frac{1}{{\mu }^{1-\alpha }}\right){\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\delta \right)-c\left(1-\alpha \right)\left(t-t_1\right)\\ \le {\mu }^{1-\alpha }\left({\phi }_2^{1-\alpha }\left(\left|x_0\right|\right)-{\psi }^{1-\alpha }\left(\left|x_0\right|\right)+\frac{1}{{\mu }^{1-\alpha }}{\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\delta \right)-c\left(1-\alpha \right)\left(t-t_1\right)\\ \le {\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\delta -c\left(1-\alpha \right)\left(t-t_1\right)\\ \le {\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\delta -\frac{t-t_1}{t_2-t_1}\delta .\end{array}$

当 $t\in \left[t_2,t_3\wedge t_1^{\wedge }\right)$ 时，我们有

$\begin{array}{c}{\nu }_{\sigma \left(t_2\right)}^{1-\alpha }\left(t\right)\le {\nu }_{\sigma \left(t_2\right)}^{1-\alpha }\left(t_1\right)-c\left(1-\alpha \right)\left(t-t_2\right)\\ \le {\mu }^{1-\alpha }{\nu }_{\sigma \left(t_1\right)}^{1-\alpha }\left(t_2^{-}\right)-c\left(1-\alpha \right)\left(t-t_2\right)\\ \le {\mu }^{1-\alpha }\left({\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\delta -c\left(1-\alpha \right)\left(t_2-t_1\right)\right)-c\left(1-\alpha \right)\left(t-t_2\right)\\ \le {\mu }^{1-\alpha }\left({\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\delta -c\left(1-\alpha \right)\tau \right)-c\left(1-\alpha \right)\left(t-t_2\right)\end{array}$

$\begin{array}{c}\le {\mu }^{1-\alpha }\left({\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\delta -\left(1-\frac{1}{{\mu }^{1-\alpha }}\right){\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\delta \right)-c\left(1-\alpha \right)\left(t-t_2\right)\\ \le {\psi }^{1-\alpha }\left(\left|x_0\right|\right)-2\delta -c\left(1-\alpha \right)\left(t-t_2\right)\\ \le {\psi }^{1-\alpha }\left(\left|x_0\right|\right)-2\delta -\frac{t-t_2}{t_3-t_2}\delta .\end{array}$

下面我们将证明

当 $t\in \left[t_k,t_{k+1}\wedge t_1^{\wedge }\right)$ 时，

${\nu }_{\sigma \left(t_k\right)}^{1-\alpha }\left(t\right)\le {\psi }^{1-\alpha }\left(\left|x_0\right|\right)-k\delta -\frac{t-t_k}{t_{k+1}-t_k}\delta$ (8)

现在假设在区间 $\left[0,t_k\right)$ 上，k满足 $1<k<N\left(t_1^{\wedge },0\right)$ 并且 $\forall t\in [t_m,t_{m+1})$ ， $m=1,\cdots ,k-1$ ，可以得到

$\begin{array}{c}{\nu }_{\sigma \left(t_m\right)}^{1-\alpha }\left(t\right)\le {\nu }_{\sigma \left(t_m\right)}^{1-\alpha }\left(t_m\right)-c\left(1-\alpha \right)\left(t-t_m\right)\\ \le {\psi }^{1-\alpha }\left(\left|x_0\right|\right)-m\delta -\frac{t-t_m}{t_{m+1}-t_m}\delta \end{array}$

在 $t\in \left[t_k,t_{k+1}\wedge t_1^{\wedge }\right)$ 时，

$\begin{array}{c}{\nu }_{\sigma \left(t_k\right)}^{1-\alpha }\left(t\right)\le {\nu }_{\sigma \left(t_k\right)}^{1-\alpha }\left(t_k\right)-c\left(1-\alpha \right)\left(t-t_k\right)\\ \le {\mu }^{1-\alpha }{\nu }_{\sigma \left(t_{k-1}\right)}^{1-\alpha }\left(t_k^{-}\right)-c\left(1-\alpha \right)\left(t-t_k\right)\\ \le {\mu }^{1-\alpha }\left({\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\left(k-1\right)\delta -c\left(1-\alpha \right)\left(t_k-t_{k-1}\right)\right)-c\left(1-\alpha \right)\left(t-t_k\right)\\ \le {\mu }^{1-\alpha }\left({\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\left(k-1\right)\delta -c\left(1-\alpha \right)\tau \right)-c\left(1-\alpha \right)\left(t-t_k\right)\end{array}$

$\begin{array}{l}\le {\mu }^{1-\alpha }\left({\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\left(k-1\right)\delta -\left(1-\frac{1}{{\mu }^{1-\alpha }}\right){\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\delta \right)-c\left(1-\alpha \right)\left(t-t_k\right)\\ \le {\psi }^{1-\alpha }\left(\left|x_0\right|\right)-k\delta -c\left(1-\alpha \right)\left(t-t_k\right)\\ \le {\psi }^{1-\alpha }\left(\left|x_0\right|\right)-k\delta -\frac{t-t_k}{t_{k+1}-t_k}\delta .\end{array}$

所以在 $\forall t\in \left[t_k,t_{k+1}\wedge t_1^{\wedge }\right)$ 上成立。通过归纳法得出，当 $N\left(t_1^{\wedge },0\right)>0$ 时，对 $\forall t\in \left[0,t_1^{\wedge }\right)$ 都成立。

如果 $t_1^{\wedge }=\infty$ ，则(8)式在 $\left[0,\infty \right)$ 上成立。如果 $t_1^{\wedge }<\infty$ ，则当 $t\in \left[t_l^{\wedge },t_l^{\vee }\right)$ 上时，由(6b)式得

${\nu }_{\sigma \left(t\right)}\left(t\right)\le \chi \left({\Vert \omega \Vert }_{[0,t]}\right)\le {\beta }_2\left(\left|x_0\right|,t-t_0\right)\vee \chi \left({\Vert \omega \Vert }_{[0,t]}\right)$

对于 $\forall t\in \left[t_{l-1}^{\vee },t_l^{\wedge }\right)$ 时，

若 $t_{l-1}^{\vee }$ 是脉冲切换时刻，则 $t_{l-1}^{\vee }<t_{{\xi }_l+1}<t_{{\xi }_l+2}<\cdots \le t_l^{\wedge }$ 。那么由(A₁)和(A₂)得

${\phi }_1\left(t_{l-1}^{\vee }\right)\le {\nu }_{\sigma \left(t_{l-1}^{\vee }\right)}\left(t_{l-1}^{\vee }\right)\le \mu v_{\sigma \left(t_{l-1}^{\vee }-1\right)}\left(t_{l-1}^{\vee -}\right)\le \mu {\phi }_2\left(\chi \left({\Vert \omega \Vert }_{\left[0,t_{l-1}^{\vee }\right)}\right)\right)$

我们有

$\left|x\left(t_{l-1}^{\vee }\right)\right|\le {\phi }_1^{-1}\left(\mu {\phi }_2\left(\chi \left({\Vert \omega \Vert }_{\left[0,t_{l-1}^{\vee }\right)}\right)\right)\right)$ (9)

若 $t_{l-1}^{\vee }$ 不是脉冲切换时刻，由(6a)和(6b)得 $\nu \left(t_{l-1}^{\vee -}\right)\le \chi \left({\Vert \omega \Vert }_{\left[0,t_{l-1}^{\vee }\right)}\right)\le \chi \left({\Vert \omega \Vert }_{\left[0,t_{l-1}^{\vee }\right]}\right)\le \nu \left(t_{l-1}^{\vee }\right)$ 。

则 $\nu \left(t_{l-1}^{\vee }\right)=\chi \left({\Vert \omega \Vert }_{\left[0,t_{l-1}^{\vee }\right]}\right)$ ，否则 $t_{l-1}^{\vee }$ 为脉冲切换时刻。又因为对于 $\forall t\in \left[t_{l-1}^{\vee },t_l^{\wedge }\right)$ ，有 $\chi \left({\Vert \omega \Vert }_{[0,t]}\right)\le \nu \left(t\right)$ 。所以我们有 $\nu \left(t_{l-1}^{\vee }\right)\le \nu \left(t\right)$ ，这与条件(A₃)矛盾，所以 $t_{l-1}^{\vee }$ 一定是脉冲切换时刻。

所以对于 $\forall t\in \left[t_{l-1}^{\vee },t_l^{\wedge }\right)$ 时，

当 $t\in [t_{l-1}^{\vee },t_{{\xi }_l+1}\wedge t_l^{\wedge })$ 时，由(7)和(9)我们可以得到

$\begin{array}{c}{\nu }_{\sigma \left(t_{l-1}^{\vee }\right)}^{1-\alpha }\left(t\right)\le {\nu }_{\sigma \left(t_{l-1}^{\vee }\right)}^{1-\alpha }\left(t_{l-1}^{\vee }\right)-c\left(1-\alpha \right)\left(t-t_{l-1}^{\vee }\right)\\ \le {\phi }_2^{1-\alpha }\left(t_{l-1}^{\vee }\right)-c\left(1-\alpha \right)\left(t-t_{l-1}^{\vee }\right)\\ \le {\phi }_2^{1-\alpha }\left({\phi }_1^{-1}\left(\mu {\phi }_2\left(\chi \left({\Vert \omega \Vert }_{\left[0,t_{l-1}^{\vee }\right)}\right)\right)\right)\right)-c\left(1-\alpha \right)\left(t-t_{l-1}^{\vee }\right)\\ \le {\psi }^{1-\alpha }\left(\left|x_0\right|\right)-c\left(1-\alpha \right)\left(t-t_{l-1}^{\vee }\right)\end{array}$

当 $t\in [t_{{\xi }_l+1},t_{{\xi }_l+2}\wedge t_l^{\wedge })$ 时，则

$\begin{array}{c}{\nu }_{\sigma \left(t_{{\xi }_l+1}\right)}^{1-\alpha }\left(t\right)\le {\nu }_{\sigma \left(t_{{\xi }_l+1}\right)}^{1-\alpha }\left(t_{{\xi }_l+1}\right)-c\left(1-\alpha \right)\left(t-t_{{\xi }_l+1}\right)\\ \le {\mu }^{1-\alpha }{\nu }_{\sigma \left(t_{l-1}^{\vee }\right)}^{1-\alpha }\left(t_{{\xi }_l+1}^{-}\right)-c\left(1-\alpha \right)\left(t-t_{{\xi }_l+1}\right)\\ \le {\mu }^{1-\alpha }\left({\phi }_2^{1-\alpha }\left({\phi }_1^{-1}\left(\mu {\phi }_2\left(\chi \left({\Vert \omega \Vert }_{\left[0,t_{{\xi }_l+1}\right)}\right)\right)\right)\right)-c\left(1-\alpha \right)\left(t_{{\xi }_l+1}-t_{l-1}^{\vee }\right)\right)-c\left(1-\alpha \right)\left(t-t_{{\xi }_l+1}\right)\\ \le {\mu }^{1-\alpha }\left({\phi }_2^{1-\alpha }\left({\phi }_1^{-1}\left(\mu {\phi }_2\left(\chi \left({\Vert \omega \Vert }_{\left[0,t_{{\xi }_l+1}\right)}\right)\right)\right)\right)-c\left(1-\alpha \right)\tau \right)-c\left(1-\alpha \right)\left(t-t_{{\xi }_l+1}\right)\\ \le {\mu }^{1-\alpha }\left({\phi }_2^{1-\alpha }\left({\phi }_1^{-1}\left(\mu {\phi }_2\left(\chi \left({\Vert \omega \Vert }_{\left[0,t_{{\xi }_l+1}\right)}\right)\right)\right)\right)-\left(1-\frac{1}{{\mu }^{1-\alpha }}\right){\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\delta \right)-c\left(1-\alpha \right)\left(t-t_{{\xi }_l+1}\right)\\ \le {\psi }^{1-\alpha }\left(\left|x_0\right|\right)-\delta -c\left(1-\alpha \right)\left(t-t_{{\xi }_l+1}\right).\end{array}$

所以，类似上面归纳结论，当 $t\in [t_{{\xi }_l+k},t_{{\xi }_l+k+1}\wedge t_l^{\wedge })$ ，则

$\begin{array}{c}{\nu }_{\sigma \left(t_{{\xi }_l+k}\right)}^{1-\alpha }\left(t\right)\le {\psi }^{1-\alpha }\left(\left|x_0\right|\right)-k\delta -c\left(1-\alpha \right)\left(t-t_{{\xi }_l+k}\right)\\ \le {\psi }^{1-\alpha }\left(\left|x_0\right|\right)-k\delta -\frac{t-t_{{\xi }_l+k}}{t_{{\xi }_l+k+1}-t_{{\xi }_l+k}}\delta .\end{array}$

综上所述，对于 $\forall t\in [0,\infty )$

${\nu }_{\sigma \left(t\right)}\left(t\right)\le {\beta }_2\left(\left|x_0\right|,t-t_0\right)\vee \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$ .

若情况(ii)成立，在这种情况下，证明方法与上面相同，我们最终可以证得

${\nu }_{\sigma \left(t\right)}\left(t\right)\le {\beta }_2\left(\left|x_0\right|,t-t_0\right)\vee \chi \left({\Vert \omega \Vert }_{[0,t]}\right)$ .

联立(A₁)和(6)式可以得到

${\phi }_1\left(\left|x\left(t\right)\right|\right)\le {\nu }_{\sigma \left(t\right)}\left(t\right)\le {\beta }_2\left(\left|x_0\right|,t-t_0\right)\vee \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$

即

$\left|x\left(t\right)\right|\le \beta \left(\left|x_0\right|,t\right)+\gamma \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$

这里 $\beta \left(s,t\right)={\phi }_1^{-1}\circ {\beta }_2\left(s,t\right)$ 是一个 $\mathcal{K}{\mathcal{L}}_0$ 函数， $\gamma \left(s\right)={\phi }_1^{-1}\left(\chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)\right)$ 是一个 ${\mathcal{K}}_{\infty }$ 函数。因此系统(1)在 $U_{\vartheta }$ 上对于任意脉冲序列 $\left\{t_k\right\}\in {\mathcal{F}}_{\tau }$ 是FTISS。得证。

注1：假设(A₃)保证了不具有脉冲效应时系统(1)是FTISS。故，当系统(1)受到稳定的脉冲扰动，即 $\mu \le 1$ 时，对于任意的脉冲频率 $\tau >0$ ，系统(1)都是FTISS的；当系统(1)受到不稳定的脉冲扰动影响，即 $\mu >1$ 时，定理2.1得到了系统(1)仍然保持FTISS性质的脉冲频率的下界，即

$\text{τ}\ge \left(1-\frac{1}{{\mu }^{1-\alpha }}\right)\frac{{\psi }^{1-\alpha }\left(\vartheta \right)}{c\left(1-\alpha \right)\tau }$ .

注2：文献 [18] 给出了在连续部分在满足 $D^{+}{V}_i{\left[x\left(t\right)\right]}_f\le -c{V}_i\left(x\left(t\right)\right)$ 时的输入输出到状态稳定。当存在不稳定的脉冲时 $\left(\mu >1\right)$ ，则脉冲切换时间序列需满足 $\tau \ge \frac{\ln \mu }{c}$ 。定理2.1的连续部分满足 $D^{+}{V}_i{\left[x\left(t\right)\right]}_f\le -c{V}_i{}^{\alpha }\left(x\left(t\right)\right)$ 且 $\alpha \in \left(0,1\right)$ ，当存在不稳定的脉冲情况时，我们可以得到FTISS的结论。

4. 数值模拟

本节给出一个数值例子说明本文中定理的正确性。

$\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)=A{x}^{\frac{1}{3}}\left(t\right)+Bx\left(t\right)+{\omega }^2\left(t\right),t\ne t_k,\\ x\left(t\right)=1.2x\left(t^{-}\right),t=t_k.\end{array}$ (10)

这里 $S\in \left\{1,2\right\}$ ， $A_1=-1.5$ ， $A_2=-2$ ， $B_1=-1.1$ ， $B_2=-1$ ， $V_1\left(x\right)=V_2\left(x\right)=\left|x\right|$ ， ${\phi }_1\left(\left|x\right|\right)={\phi }_2\left(\left|x\right|\right)=\left|x\right|$ ，根据定理，当 $t=t_k$ 时， $V_i\left(g\left(x\left(t\right)\right)\right)=\left|1.2x\left(t^{-}\right)\right|\le 1.2x\left(t^{-}\right)$ ， $i\in S$ 。

对于所有的 $\left\{1,2\right\}\in S$ ，当 $V_i\left(x\left(t\right)\right)\ge {\omega }^2\left(t\right)$ 时，我们有

$\begin{array}{c}{\stackrel{\dot{}}{V}}_1\left(x\left(t\right)\right)\le -1.5{\left|x\left(t\right)\right|}^{\frac{1}{3}}-1.1\left|x\left(t\right)\right|+{\omega }^2\left(t\right)\\ \le -1.5{\left|x\left(t\right)\right|}^{\frac{1}{3}}-0.1\left|x\left(t\right)\right|-\left(\left|x\left(t\right)\right|-{\omega }^2\left(t\right)\right)\\ \le -1.5V_1{\left(x\left(t\right)\right)}^{\frac{1}{3}}-0.1V_1\left(x\left(t\right)\right),\end{array}$

$\begin{array}{c}{\stackrel{\dot{}}{V}}_2\left(x\left(t\right)\right)\le -2{\left|x\left(t\right)\right|}^{\frac{1}{3}}-1\left|x\left(t\right)\right|+{\omega }^2\left(t\right)\\ \le -2{\left|x\left(t\right)\right|}^{\frac{1}{3}}-\left(\left|x\left(t\right)\right|-{\omega }^2\left(t\right)\right)\\ \le -2V_2{\left(x\left(t\right)\right)}^{\frac{1}{3}},\end{array}$

${\stackrel{\dot{}}{V}}_{\sigma \left(t\right)}\left(x\left(t\right)\right)\le -1.5V_{\sigma \left(t\right)}{\left(x\left(t\right)\right)}^{\frac{1}{3}},t\ne t_k$ .

所以条件(A₁)、(A₂)和(A₃)都成立。 $c=1.5$ ， $\mu =1.2$ ， $\alpha =\frac{1}{3}$ 。因此，对于 $\forall \left\{t_k\right\}\in {\mathcal{F}}_{\tau }$ 且

$\tau \ge \frac{\left(1-\frac{1}{{\mu }^{1-\alpha }}\right){\psi }^{1-\alpha }\left(\vartheta \right)}{c\left(1-\alpha \right)}=2\left(1-\frac{1}{1.13}\right){\psi }^{1-\alpha }(\; \vartheta \; )$

则系统(11)是FTISS，这里 $\psi \left(\vartheta \right)$ 在定理2.1中已定义。取 $\vartheta =5$ ， $\omega \left(t\right)=0.5\left(1+\sin t\right)$ 。此时， ${\Vert \omega \Vert }_{\infty }=1$ 和 $\psi \left(\vartheta \right)=5$ ，从而我们有冲频率 $\tau \ge 0.39$ 。在数值模拟中，取 $t_k=k$ ， $k\in {\mathbb{Z}}_0$ 时， $\tau =1\ge 0.39$ 。此时图1显示了系统(10)在初始状态 $x_0=5$ 时的轨迹在有限时刻进入 $\gamma \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$ 的界，此后并没有超过这个界。另一方面，在相同条件下，取 $t=0.3k$ ， $k\in {\mathbb{Z}}_0$ ，这不满足FDT的约束条件，从图2上可以看出轨道不时超过界 $\gamma \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$ 。图3和图4分别给出了t = k和t = 0.3k时系统的切换信号。

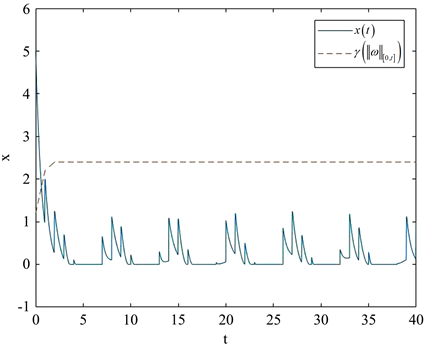
Figure 1. The trajectory of the system when t = k

图1. 当t = k时的系统轨迹

Figure 2. The trajectory of the system when t = 0.3k

图2. 当t = 0.3k时的系统轨迹

Figure 3. The switching signal of the system when t = k

图3. 当t = k时系统的切换信号

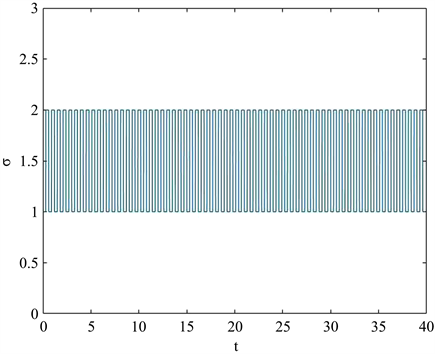
Figure 4. The switching signal of the system when t = 0.3k

图4. 当t = 0.3k时系统的切换信号

注3：文献 [19] 中研究了非线性脉冲系统的有限时间输入到状态稳定，本例扩展到脉冲切换系统。在存在多个子系统的情况下，虽然存在不稳定的脉冲，但在满足脉冲切换时间序列的条件下仍然可以做到有限时间输入到状态稳定。