具有Beddington-DeAngelis型功能反应的离散捕食者–食饵系统的动力学行为

Dynamical Behavior of Discrete Predator-Prey System with Beddington-Deangelis Functional Response

摘要: 在本文中，我们提出了一个离散的具有Beddington-DeAngelis型功能反应的捕食者–食饵系统。研究了该模型不动点的稳定性。同时，利用分支理论和近似流的方法，证明了离散模型经历了折分支和翻转分支。数值模拟不仅证明了我们的理论分析的一致性，而且还展示了复杂的动力学行为，如周期为2的倍周期分支级联和混沌集。数值计算了最大李雅普诺夫指数，进一步证实了动力学行为的复杂性。结果表明，离散模型比连续模型具有更丰富的动力学特性。

Abstract: In this paper, we propose a discrete Beddington-DeAngelis predator-prey system. The stability of the fixed points of this model is studied. At the same time, it is shown that the discrete model un-dergoes fold bifurcation and flips bifurcation by using bifurcation theory and the method of ap-proximation by a flow. Numerical simulation are presented not only to demonstrate the consistence with our theoretical analyses, but also to exhibit the complex dynamical behaviors, such as the cas-cade of period-doubling bifurcation in period-2 and the chaotic sets. The Maximum Lyapunov expo-nents are numerically computed to confirm further the complexity of the dynamical behaviors. These results show that the discrete model has more rich dynamic behaviors than the continuous model.

1. 引言

捕食者与猎物之间的相互作用一直是生态学和数学生态学研究的课题。近年来，离散动力学模型得到了广泛的研究。与连续动力系统相比，离散动力系统具有以下三大优点：首先，当种群的代数不重叠或种群数量较小时，离散动力系统比连续动力系统更合适；其次，离散动力系统的数值模拟结果比连续动力系统的数值模拟结果更准确。最后，离散模型比相应的连续模型表现出更复杂的动力学行为。例如，单物种离散Logistic模型具有更复杂的动力学行为，如分支和混沌。

功能反应函数是描述单位时间内捕食者对猎物消耗率的函数，通常有两种类型：仅依赖于猎物的函数和同时依赖于猎物及捕食者密度的函数。依赖于猎物的功能反应函数，如Holling-I [1] 型功能反应函数是基于捕食者之间除了猎物消耗之外不相互竞争的假设。然而，一方面，竞争是存在的，特别是在猎物资源短缺的情况下，另一方面，捕食者不仅需要时间来寻找和处理猎物，而且与其他捕食者相遇也需要耗费一定的时间。为了描述捕食者之间的相互作用，Beddington [2] 和DeAngelis [3] 在1975年分别提出了下面的功能反应函数(现称之为Beddington-DeAngelis功能反应函数)。

$p\left(x,y\right)=\frac{mx}{ax+by+c}$ (1.1)

其中 $x\left(t\right)$ 和 $y\left(t\right)$ 分别表示在离散时间t下的食饵和捕食者的种群密度； $by$ 描述捕食者之间的干扰；

在1975年，Beddington [2] 和DeAngelis [3] 研究了下列捕食者–食饵模型：

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=rx\left(1-\frac{x}{k}\right)-p\left(x,y\right)y,\\ \frac{\text{d}y}{\text{d}}=ep\left(x,y\right)y-dy,\end{array}$ (1.2)

其中 $p\left(x,y\right)$ 采用(1.1)的形式。这类具有Beddington-DeAngelis型功能反应的模型被广泛研究，其全局动力学行为得到了很好的研究 [4] [5] [6] [7] [8] 。Hwang [5] 利用散度判据证明了当正平衡点是局部渐近稳定时，系统(1.2)不存在周期解。沈怡心 [7] 利用上下解、logistic方程以及比较原理研究了具有Beddington-DeAngelis型功能反应的非自治捕食–被捕食系统的渐进行为。Zhang [8] 研究了一个具有Beddington-DeAngelis型功能反应和捕食者竞争的捕食者–食饵模型，证明了模型存在Bogdanov-Takens分支和余维至少为2的退化Hopf分支。

为了得到一个简化的离散模型，我们先进行以下缩放

$x=\frac{bd}{a}X$ , $y=dY$ , $t=\frac{1}{d}\tau$ ,

则模型(1.2)变成了(为了简单起见，我们仍然分别用x，y和t表示X，Y和 $\tau$ )

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=\delta x-\eta x^2-\frac{\alpha xy}{x+y+\gamma },\\ \frac{\text{d}y}{\text{d}t}=-y+\frac{\beta xy}{x+y+\gamma },\end{array}$ (1.3)

其中

$\alpha =\frac{m}{bd}$ , $\beta =\frac{em}{ad}$ , $\delta =\frac{r}{d}$ , $\eta =\frac{rb}{ak}$ , $\gamma =\frac{c}{bd}$ ,

且 $\alpha$ ， $\beta$ ， $\delta$ ， $\eta$ 和 $\gamma$ 都是正数。

对系统(1.3)应用欧拉一步迭代方法(该方法已在文献 [9] 中使用)，我们得到离散系统

$\{\begin{array}{l}x\left(n+1\right)=x\left(n\right)+\delta x\left(n\right)-\eta x^2\left(n\right)-\frac{\alpha x\left(n\right)y\left(n\right)}{x\left(n\right)+y\left(n\right)+\gamma },\\ y\left(n+1\right)=\frac{\beta x\left(n\right)y\left(n\right)}{x\left(n\right)+y\left(n\right)+\gamma }.\end{array}$ (1.4)

本文研究上述离散的具有Beddington-DeAngelis型功能反应的捕食者–食饵系统，利用分支理论和近似流的方法，得到了边界平衡点存在折分支和翻转分支的条件，并通过数值模拟证明了相应的理论分析。

2. 预备知识

本章主要介绍了相关的定义、定理等基本理论知识，为后面章节的研究工作做准备。

定义2.1 [9]

1) 若 $\left|{\lambda }_1\right|<1$ 且 $\left|{\lambda }_2\right|<1$ ，则称不动点E为汇点，并且不动点是局部渐近稳定的。

2) 若 $\left|{\lambda }_1\right|>1$ 且 $\left|{\lambda }_2\right|>1$ ，则称不动点E为源点，并且不动点是局部不稳定的。

3) 若 $\left|{\lambda }_1\right|<1$ 且 $\left|{\lambda }_2\right|>1$ (或 $\left|{\lambda }_1\right|>1$ 且 $\left|{\lambda }_2\right|<1$ )，则称不动点E为鞍点。

4) 若 $\left|{\lambda }_1\right|=1$ 或者 $\left|{\lambda }_2\right|=1$ ，则称不动点E为非双曲点。

定理2.2 [10] 令 $F\left(\lambda \right)={\lambda }^2+B\lambda +C$ ， ${\lambda }_1$ 和 ${\lambda }_2$ 为 $F\left(\lambda \right)=0$ 的两个根，则下列结论成立：

1) 如果 $F\left(1\right)>0$ ，那么

(1.1) 当且仅当 $F\left(-1\right)>0$ 且 $C<1$ 时，有 $\left|{\lambda }_1\right|<1$ 且 $\left|{\lambda }_2\right|<1$ 成立；

(1.2) 当且仅当 $F\left(-1\right)<0$ 时，有 $\left|{\lambda }_1\right|<1$ 且 $\left|{\lambda }_2\right|>1$ (或者 $\left|{\lambda }_1\right|>1$ 且 $\left|{\lambda }_2\right|<1$ )成立；

(1.3) 当且仅当 $F\left(-1\right)>0$ 且 $C>1$ 时，有 $\left|{\lambda }_1\right|>1$ 且 $\left|{\lambda }_2\right|>1$ 成立；

(1.4) 当且仅当 $F\left(-1\right)=0$ 且 $B\ne 0,2$ 时，有 ${\lambda }_1=-1$ 且 $\left|{\lambda }_2\right|\ne 1$ 成立；

(1.5) 当且仅当 $F\left(-1\right)=0$ 且 $B=2$ 时，有 ${\lambda }_1=-1$ 且 ${\lambda }_2=-1$ 成立；

(1.6) 当且仅当 $B^2-4C<0$ 且 $C=1$ 时， ${\lambda }_1$ 和 ${\lambda }_2$ 是复数且 $\left|{\lambda }_1\right|=\left|{\lambda }_2\right|=1$ 。

2) 如果 $F\left(1\right)=0$ ，那么

(2.1) 当且仅当 $\left|C\right|\ne 1$ 时，有 ${\lambda }_1=1$ 且 $\left|{\lambda }_2\right|\ne 1$ 成立；

(2.2) 当且仅当 $\left|C\right|=1$ 时，有 ${\lambda }_1=1$ 且 $\left|{\lambda }_2\right|=1$ 成立；

3) 如果 $F\left(1\right)<0$ ，那么 ${\lambda }_1>1$ 且

(3.1) 当且仅当 $F\left(-1\right)<0$ 时，有 ${\lambda }_1>1$ 且 $\left|{\lambda }_2\right|>1$ 成立；

(3.2) 当且仅当 $F\left(-1\right)>0$ 时，有 ${\lambda }_1>1$ 且 $\left|{\lambda }_2\right|<1$ 成立；

(3.3) 当且仅当 $F\left(-1\right)=0$ 时，有 ${\lambda }_1>1$ 且 ${\lambda }_2=1$ 成立。

3. 不动点的存在性和稳定性

在本节中，我们给出了系统(1.4)在 $R_{+}^2$ 空间的不动点存在的条件，以及讨论了不动点的稳定性。

显然，系统(1.4)的不动点满足如下方程组：

$\{\begin{array}{l}x=x+\delta x-\eta x^2-\frac{\alpha xy}{x+y+\gamma },\\ y=\frac{\beta xy}{x+y+\gamma }.\end{array}$ (3.1)

通过简单的计算，我们得到如下引理。

引理3.1系统(3.3)有三个不动点 $O=\left(0,0\right)$ ， $A=\left(\frac{\delta }{\eta },0\right)$ 和 $B=\left(x^{\ast },y^{\ast }\right)$ ，其中 $x^{\ast }=\frac{-\left(\alpha \beta -\delta \beta -\alpha \right)+\sqrt{\Delta }}{2\beta \eta }$ ， $y^{\ast }=\left(\beta -1\right)x^{\ast }-\gamma$ 和 $\Delta ={\left(\alpha \beta -\delta \beta -\alpha \right)}^2+4\alpha \beta \eta \gamma$ 。

接下来，我们研究系统(1.4)在不动点处的稳定性。系统(1.4)在 $E\left(x,y\right)$ 处的Jacobian矩阵如下：

$J\left(x,y\right)=\left(\begin{array}{cc}1+\delta -2\eta x-\frac{\alpha y\left(y+\gamma \right)}{{\left(x+y+\gamma \right)}^2}& -\frac{\alpha x\left(x+\gamma \right)}{{\left(x+y+\gamma \right)}^2}\\ \frac{\beta y\left(y+\gamma \right)}{{\left(x+y+\gamma \right)}^2}& \frac{\beta x\left(x+\gamma \right)}{{\left(x+y+\gamma \right)}^2}\end{array}\right),$ (3.2)

矩阵的特征方程可表示为

${\lambda }^2+p\left(x,y\right)\lambda +q\left(x,y\right)=0$ ,

其中

$p\left(x,y\right)=-1-\delta +2\eta x+\frac{\alpha y\left(y+\gamma \right)}{{\left(x+y+\gamma \right)}^2}-\frac{\beta x\left(x+\gamma \right)}{{\left(x+y+\gamma \right)}^2}$ ,

$q\left(x,y\right)=\left(1+\delta -2\eta x\right)\frac{\beta x\left(x+\gamma \right)}{{\left(x+y+\gamma \right)}^2}$ .

命题3.2对于任意参数，平衡点 $O=\left(0,0\right)$ 为鞍点。

命题3.3系统(3.3)存在边界平衡点 $A=\left(\frac{\delta }{\eta },0\right)$ ，并且

1) 当 $0<\delta <2$ 和 $0<\beta <\frac{\gamma \eta }{\delta }+1$ 时，不动点A是汇点；

2) 当 $\delta >2$ 和 $\beta >\frac{\gamma \eta }{\delta }+1$ 时，不动点A是源点；

3) 当 $\delta =2$ 或 $\beta =\frac{\gamma \eta }{\delta }+1$ 时，不动点A是非双曲的；

其他条件下，不动点A是鞍点。

证明 不动点A的Jacobian矩阵是

${J|}_A=\left(\begin{array}{cc}1-\delta & -\frac{\alpha \delta }{\gamma \eta +\delta }\\ 0& \frac{\beta \delta }{\gamma \eta +\delta }\end{array}\right).$ (3.3)

特征方程的两个特征值为：

${\lambda }_1=1-\delta$ ; ${\lambda }_2=\frac{\beta \delta }{\gamma \eta +\delta }$ .

当 $\left|{\lambda }_i\right|<1$ ( $i=1,2$ )时，不动点 $A=\left(\frac{\delta }{\eta },0\right)$ 为汇聚点。则有

$\left|{\lambda }_1\right|=\left|1-\delta \right|<1\Rightarrow 0<\delta <2$ ,

$\left|{\lambda }_2\right|=\left|\frac{\beta \delta }{\gamma \eta +\delta }\right|<1\Rightarrow 0<\beta <\frac{\gamma \eta }{\delta }+1$ .

因此，满足以下条件，不动点 $A=\left(\frac{\delta }{\eta },0\right)$ 是稳定的：

$0<\delta <2,0<\beta <\frac{\gamma \eta }{\delta }+1.$

其他三个命题用上述方法可证，命题3.2得证。

条件(3)可以写成如下形式：

$F{B}_A^1=\left\{\left(\alpha ,\beta ,\gamma ,\eta ,\delta \right)\in \left(0,+\infty \right):\beta =\frac{\gamma \eta }{\delta }+1,\delta \ne 1,2\right\},$ (3.4)

$F{B}_A^2=\left\{\left(\alpha ,\beta ,\gamma ,\eta ,\delta \right)\in \left(0,+\infty \right):\delta =2,\beta \ne \frac{\gamma \eta }{\delta }+1\right\}.$ (3.5)

为了后面计算方便，令

$\Delta ={\left(\alpha \beta -\delta \beta -\alpha \right)}^2+4\alpha \beta \eta \gamma$ 和 $R_1=\frac{\alpha \beta -\delta \beta -\alpha -\sqrt{\Delta }}{2\beta \eta }-\frac{\beta }{2\eta }+\frac{\left(\delta +1\right){\beta }^2}{2\eta \left[\alpha \beta -\alpha +\beta -\sqrt{\Delta }\right]}$

$R_2=\frac{\alpha \beta -\delta \beta -\alpha -\sqrt{\Delta }}{2\beta \eta }+\frac{\left(\sqrt{\Delta }-2\beta \right)\left[-\left(\alpha \beta -\delta \beta -\alpha \right)+\sqrt{\Delta }\right]}{2\eta \left[2\left(\alpha \beta -\alpha +\beta \right)-\sqrt{\Delta }\right]}$ .

命题3.4 系统(1.4)存在正平衡点 $B=\left(x^{\ast },y^{\ast }\right)$ ，其中 $x^{\ast }=\frac{-\left(\alpha \beta -\delta \beta -\alpha \right)+\sqrt{\Delta }}{2\beta \eta }$ ， $y^{\ast }=\left(\beta -1\right)x^{\ast }-\gamma$ ，并且

1) 当 $\beta \ne 1$ ， $\delta >\frac{\gamma \eta }{\beta -1}$ 和 $R_2<\gamma <R_1$ 时，不动点B是汇点。

2) 满足以下条件之一时，不动点B是源点：

(2.1) $\beta \ne 1$ ， $\delta >\frac{\gamma \eta }{\beta -1}$ 和 $\gamma >\max \left\{R_1,R_2\right\}$ ；

(2.2) $\beta >1$ ， $\delta <\frac{\gamma \eta }{\beta -1}$ 和 $\gamma <R_2$ ；

(2.3) $\beta =1$ 和 $\gamma <R_2$ ；

3) 满足以下条件之一时，不动点B是非双曲的：

(3.1) $\gamma =R_1$ ；

(3.2) $\gamma =R_2$ ；

(3.3) $\beta \ne 1$ 和 $\delta =\frac{\gamma \eta }{\beta -1}$ 。

4) 其他条件下，不动点B是鞍点。

证明不动点B的Jacobian矩阵是

${J|}_B=\left(\begin{array}{cc}1+\delta -2\eta x^{\ast }-\frac{\alpha y^{\ast }\left(y^{\ast }+\gamma \right)}{{\left(x^{\ast }+y^{\ast }+\gamma \right)}^2}& -\frac{\alpha x^{\ast }\left(x^{\ast }+\gamma \right)}{{\left(x^{\ast }+y^{\ast }+\gamma \right)}^2}\\ \frac{\beta y^{\ast }\left(y^{\ast }+\gamma \right)}{{\left(x^{\ast }+y^{\ast }+\gamma \right)}^2}& \frac{\beta x^{\ast }\left(x^{\ast }+\gamma \right)}{{\left(x^{\ast }+y^{\ast }+\gamma \right)}^2}\end{array}\right),$ (3.6)

经过计算，得到 $J\left(x^{\ast },y^{\ast }\right)$ 的特征方程如下：

${\lambda }^2+B\lambda +C=0$ ,

其中 $B=-1+\frac{\sqrt{\Delta }-\alpha -1}{\beta }+\frac{\alpha }{{\beta }^2}-\frac{2\gamma \eta \left(\beta -\alpha +\alpha \beta \right)}{-\beta \left(\alpha \beta -\delta \beta -\alpha \right)+\beta \sqrt{\Delta }}$ ，

$C=\frac{\alpha +1}{\beta }-\frac{\alpha +\sqrt{\Delta }}{{\beta }^2}+\frac{2\gamma \eta \left(\beta -\alpha +\alpha \beta -\sqrt{\Delta }\right)}{-\beta \left(\alpha \beta -\delta \beta -\alpha \right)+\beta \sqrt{\Delta }}$ .

为了方便计算，令

$F\left(\lambda \right)={\lambda }^2+B\left(x^{\ast },y^{\ast }\right)\lambda +C\left(x^{\ast },y^{\ast }\right)$ .

则， $F\left(1\right)=\frac{\sqrt{\Delta }}{\beta }\left(1-\frac{1}{\beta }-\frac{2\gamma \eta }{-\left(\alpha \beta -\delta \beta -\alpha \right)+\sqrt{\Delta }}\right)$ ，

$F\left(-1\right)=2+\frac{2\left(\alpha +1\right)-\sqrt{\Delta }}{\beta }-\frac{2\alpha +\sqrt{\Delta }}{{\beta }^2}+\frac{4\gamma \eta \left(\alpha \beta -\alpha +\beta \right)-2\gamma \eta \sqrt{\Delta }}{-\beta \left(\alpha \beta -\delta \beta -\alpha \right)+\beta \sqrt{\Delta }}$ ,

根据定理2.2可知， $\left|{\lambda }_1\right|<1$ 和 $\left|{\lambda }_2\right|<1$ 当且仅当 $F\left(1\right)>0$ ， $F\left(-1\right)>0$ 和 $C<1$ 。则 $F\left(1\right)>0\Rightarrow \left(\beta -1\right)\left[-\left(\alpha \beta -\delta \beta -\alpha \right)+\sqrt{\Delta }\right]>2\beta \gamma \eta$ ，

如果 $\beta >1$ ，那么 $\delta >\frac{\gamma \eta }{\beta -1}$ ；

如果 $\beta =1$ ，则不等式不成立；

如果 $\beta <1$ ，由于 $-\left(\alpha \beta -\delta \beta -\alpha \right)+\sqrt{\Delta }>0$ ，而 $\frac{2\gamma \eta \beta }{\beta -1}<0$ ，那么不等式不成立；

$\begin{array}{c}F\left(-1\right)>0\Rightarrow \gamma \eta \left[4\left(\alpha \beta -\alpha +\beta \right)-2\sqrt{\Delta }\right]>\left(\sqrt{\Delta }-2\beta \right)\left[-\left(\alpha \beta -\delta \beta -\alpha \right)+\sqrt{\Delta }\right]\\ +\frac{\left[-2\left(\alpha \beta -\alpha +\beta \right)+\sqrt{\Delta }\right]\left[-\left(\alpha \beta -\delta \beta -\alpha \right)+\sqrt{\Delta }\right]}{\beta }\\ \Rightarrow \gamma >R_2,\end{array}$

$\begin{array}{c}C>1\Rightarrow 2\gamma \eta \left(\alpha \beta -\alpha +\beta -\sqrt{\Delta }\right)>\frac{\left(\alpha \beta -\alpha +\beta -\sqrt{\Delta }\right)\left(\alpha \beta -\delta \beta -\alpha -\sqrt{\Delta }\right)}{\beta }\\ -\beta \left(\alpha \beta -\alpha +\beta -\sqrt{\Delta }\right)+\left(\delta +1\right){\beta }^2\\ \Rightarrow \gamma >R_1,\end{array}$

由 $F\left(1\right)>0$ ， $F\left(-1\right)>0$ 和 $C<1$ 得到结论(1)，同理可得结论(2)和(3)。命题3.4得证。

4. 折分支

由命题3.3 (3)可知，当 $\beta =\frac{\gamma \eta }{\delta }+1$ 和 $\delta \ne 2$ 时， $A\left(\frac{\delta }{\eta },0\right)$ 处的特征值为 ${\lambda }_1=1-\delta$ 和 ${\lambda }_2=1$ 。

为了将不动点 $A\left(\frac{\delta }{\eta },0\right)$ 转移至原点 $O\left(0,0\right)$ 研究，令 $u\left(n\right)=x\left(n\right)-\frac{\delta }{\eta }$ ， $v\left(n\right)=y\left(n\right)$ 和 ${\beta }^{\ast }=\beta -\frac{\gamma \eta }{\delta }-1$ 。经过泰勒展开，系统(1.4)转换为

$\left(\begin{array}{l}u\left(n+1\right)\\ v\left(n+1\right)\end{array}\right)=\left(\begin{array}{cc}1-\delta & -\frac{\alpha \delta }{\gamma \eta +\delta }\\ 0& 1\end{array}\right)\left(\begin{array}{l}u\left(n\right)\\ v\left(n\right)\end{array}\right)+\left(\begin{array}{l}{F}_1\left(u\left(n\right),v\left(n\right),{\beta }^{\ast }\right)\\ F_2\left(u\left(n\right),v\left(n\right),{\beta }^{\ast }\right)\end{array}\right),$ (4.1)

其中 $U={\left(u\left(n\right),v\left(n\right)\right)}^{\text{T}}$ ，

$\begin{array}{c}{F}_1\left(u\left(n\right),v\left(n\right),{\beta }^{\ast }\right)=-\eta u^2\left(n\right)+\frac{\alpha \eta \delta }{{\left(\gamma \eta +\delta \right)}^2}{v}^2\left(n\right)-\frac{\alpha {\eta }^2\gamma }{{\left(\gamma \eta +\delta \right)}^2}u\left(n\right)v\left(n\right)-\frac{\alpha {\eta }^2\delta }{{\left(\gamma \eta +\delta \right)}^3}{v}^3\left(n\right)\\ -\frac{\alpha {\eta }^2\left(\delta -\eta \gamma \right)}{{\left(\gamma \eta +\delta \right)}^3}u\left(n\right)v^2\left(n\right)+\frac{\alpha {\eta }^3\gamma }{{\left(\gamma \eta +\delta \right)}^3}u\left(n\right)v\left(n\right)+O\left({\Vert U\Vert }^4\right),\end{array}$

$\begin{array}{c}{F}_1\left(u\left(n\right),v\left(n\right),{\beta }^{\ast }\right)=\frac{{\beta }^{\ast }\delta }{\gamma \eta +\delta }v\left(n\right)-\frac{\eta \left({\beta }^{\ast }\delta +\gamma \eta +\delta \right)}{{\left(\gamma \eta +\delta \right)}^2}{v}^2\left(n\right)+\frac{{\eta }^2\gamma \left({\beta }^{\ast }\delta +\gamma \eta +\delta \right)}{\delta {\left(\gamma \eta +\delta \right)}^2}u\left(n\right)v\left(n\right)\\ +\frac{{\eta }^2\left({\beta }^{\ast }\delta +\gamma \eta +\delta \right)}{{\left(\gamma \eta +\delta \right)}^3}{v}^3\left(n\right)-\frac{{\eta }^3\gamma \left({\beta }^{\ast }\delta +\gamma \eta +\delta \right)}{\delta {\left(\gamma \eta +\delta \right)}^3}{u}^2\left(n\right)v\left(n\right)\\ +\left[\frac{{\eta }^2\left({\beta }^{\ast }\delta +\gamma \eta +\delta \right)}{{\left(\gamma \eta +\delta \right)}^3}-\frac{{\eta }^3\gamma \left({\beta }^{\ast }\delta +\gamma \eta +\delta \right)}{\delta {\left(\gamma \eta +\delta \right)}^3}\right]u\left(n\right)v^2\left(n\right)+O\left({\Vert U\Vert }^4\right),\end{array}$

当 $\delta \ne 2$ 时，我们构造了一个可逆矩阵

$T_1=\left(\begin{array}{cc}1& -\alpha \\ 0& \gamma \eta +\delta \end{array}\right)$ .

令 $\left(\begin{array}{c}u\left(n\right)\\ v\left(n\right)\end{array}\right)=T_1\left(\begin{array}{c}\tilde{x}\left(n\right)\\ \tilde{y}\left(n\right)\end{array}\right)$ 。在此非退化变换下，将系统(4.1)转换为如下标准形式：

$\left(\begin{array}{l}\tilde{x}\left(n+1\right)\\ \tilde{y}\left(n+1\right)\end{array}\right)=\left(\begin{array}{cc}1-\delta & 0\\ 0& 1\end{array}\right)\left(\begin{array}{l}\tilde{x}\left(n\right)\\ \tilde{y}\left(n\right)\end{array}\right)+\left(\begin{array}{l}{g}_1\left(\tilde{x}\left(n\right),\tilde{y}\left(n\right),{\beta }^{\ast }\right)\\ g_2\left(\tilde{x}\left(n\right),\tilde{y}\left(n\right),{\beta }^{\ast }\right)\end{array}\right),$ (4.2)

其中

$\begin{array}{c}{g}_1\left(\tilde{x}\left(n\right),\tilde{y}\left(n\right),{\beta }^{\ast }\right)=\frac{{\beta }^{\ast }\alpha \delta }{\gamma \eta +\delta }\tilde{y}\left(n\right)-\eta {\tilde{x}}^2\left(n\right)+\left[\frac{\alpha {\eta }^2\gamma {\beta }^{\ast }}{{\left(\gamma \eta +\delta \right)}^2}+\frac{\left(1-\delta \right)\alpha {\eta }^2\gamma }{\delta \left(\gamma \eta +\delta \right)}+2\alpha \eta \right]\tilde{x}\left(n\right)\tilde{y}\left(n\right)\\ +\left[\alpha \eta \left(\delta -\alpha -1\right)-\frac{\alpha \eta \delta {\beta }^{\ast }}{\gamma \eta +\delta }-\frac{{\alpha }^2{\eta }^2\gamma {\beta }^{\ast }}{{\left(\gamma \eta +\delta \right)}^2}+\frac{\left(\delta -1\right){\alpha }^2{\eta }^2\gamma }{\delta \left(\gamma \eta +\delta \right)}\right]{\tilde{y}}^2\left(n\right)\\ +\left[\frac{\alpha {\eta }^2{\beta }^{\ast }\left[\left(\delta -\gamma \eta \right)\left(\gamma \eta +\delta \right)+\alpha \eta \gamma \left(2-\alpha \right)\right]}{{\left(\gamma \eta +\delta \right)}^2}-\frac{\alpha {\eta }^2\left(\delta -1\right)\left(\gamma \eta -\delta \right)}{\delta \left(\gamma \eta +\delta \right)}\right]\tilde{x}\left(n\right){\tilde{y}}^2\left(n\right)\\ +\frac{\left(2-2\delta -\alpha \right){\alpha }^2{\eta }^3\gamma }{\delta {\left(\gamma \eta +\delta \right)}^2}\tilde{x}\left(n\right){\tilde{y}}^2\left(n\right)+\left[\frac{\alpha {\eta }^3\gamma \left(\delta -1\right)}{\delta {\left(\gamma \eta +\delta \right)}^2}-\frac{\alpha {\eta }^3\gamma {\beta }^{\ast }}{{\left(\gamma \eta +\delta \right)}^3}\right]{\tilde{x}}^2\left(n\right)\tilde{y}\left(n\right)\\ +\left[\frac{\alpha {\eta }^2\delta {\beta }^{\ast }}{\gamma \eta +\delta }+\frac{{\alpha }^2{\eta }^2{\beta }^{\ast }\left(\gamma \eta -\delta \right)}{{\left(\gamma \eta +\delta \right)}^2}-\frac{{\alpha }^3{\eta }^3\gamma {\beta }^{\ast }}{{\left(\gamma \eta +\delta \right)}^3}\right]{\tilde{y}}^3\left(n\right)\\ +\left[\alpha {\eta }^2+\frac{{\alpha }^2{\eta }^2\left(\delta -1\right)\left(\delta -\gamma \eta \right)}{\delta \left(\gamma \eta +\delta \right)}+\frac{{\alpha }^3{\eta }^3\gamma \left(\delta -1\right)}{\delta {\left(\gamma \eta +\delta \right)}^2}\right]{\tilde{y}}^3\left(n\right),\end{array}$

$\begin{array}{c}{g}_2\left(\tilde{x}\left(n\right),\tilde{y}\left(n\right),{\beta }^{\ast }\right)=\frac{{\beta }^{\ast }\delta }{\gamma \eta +\delta }\tilde{y}\left(n\right)+\left[\frac{{\eta }^2\gamma {\beta }^{\ast }}{{\left(\gamma \eta +\delta \right)}^2}+\frac{{\eta }^2\gamma }{\delta \left(\gamma \eta +\delta \right)}\right]\tilde{x}\left(n\right)\tilde{y}\left(n\right)\\ +\left[-\eta -\frac{\eta \delta {\beta }^{\ast }}{\gamma \eta +\delta }-\frac{\alpha {\eta }^2\gamma {\beta }^{\ast }}{{\left(\gamma \eta +\delta \right)}^2}+\frac{\alpha {\eta }^2\gamma }{\delta \left(\gamma \eta +\delta \right)}\right]{\tilde{y}}^2\left(n\right)+\frac{{\eta }^3\gamma \left(\gamma \eta +2\delta \right)}{\delta {\left(\gamma \eta +\delta \right)}^3}{\tilde{x}}^2\left(n\right)\tilde{y}\left(n\right)\\ +\left[\frac{{\eta }^2{\beta }^{\ast }\left({\delta }^2-{\gamma }^2{\eta }^2+2\alpha \eta \gamma \right)}{{\left(\gamma \eta +\delta \right)}^2}+\frac{{\eta }^2\left(\delta -\gamma \eta \right)}{\delta \left(\gamma \eta +\delta \right)}+\frac{2\alpha {\eta }^3\gamma }{\delta {\left(\gamma \eta +\delta \right)}^3}\right]\tilde{x}\left(n\right){\tilde{y}}^2\left(n\right)\\ +\left[\frac{{\eta }^2\delta {\beta }^{\ast }}{\gamma \eta +\delta }+\frac{\alpha {\eta }^2{\beta }^{\ast }\left({\gamma }^2{\eta }^2-{\delta }^2-\alpha \gamma \eta \right)}{{\left(\gamma \eta +\delta \right)}^3}+{\eta }^2+\frac{\alpha {\eta }^2\left({\gamma }^2{\eta }^2-{\delta }^2-\alpha \gamma \eta \right)}{\delta {\left(\gamma \eta +\delta \right)}^2}\right]{\tilde{y}}^3\left(n\right).\end{array}$

通过中心流形定理和文献 [1] 的方法可知，在原点处 ${\beta }^{\ast }=0$ 的小邻域内存在系统(4.2)的中心流形 $M^c\left(0\right)$ ，其近似表示如下：

$M^c\left(0\right)=\left\{\left(\tilde{x}\left(n\right),\tilde{y}\left(n\right),{\beta }^{\ast }\right)\in R^3|\tilde{x}\left(n\right)=h\left(\tilde{y}\left(n\right),{\beta }^{\ast }\right),h\left(0,0\right)=0,Dh\left(0,0\right)=0\right\}$ .

对所有充分小的 $\tilde{y}\left(n\right)$ 和 ${\beta }^{\ast }$ ，假设中心流形的形式为

$h\left(\tilde{y}\left(n\right),{\beta }^{\ast }\right)=b_0{\beta }^{\ast }+b_1{\beta }^{\ast }\tilde{y}\left(n\right)+b_2{\left({\beta }^{\ast }\right)}^2+b_3{\tilde{y}}^2\left(n\right)+O\left({\left(\left|\tilde{y}\left(n\right)\right|+\left|{\beta }^{\ast }\right|\right)}^3\right)$ ,

其中 $O\left({\left(\left|\tilde{y}\left(n\right)\right|+\left|{\beta }^{\ast }\right|\right)}^3\right)$ 是一个至少有三个变量阶的函数。下面我们通过待定系数法求出系数 $b_i\left(i=0,1,2,3\right)$ ，由中心流形的近似表示可知

$\begin{array}{c}\tilde{x}\left(n+1\right)=h\left(\tilde{y}\left(n+1\right),{\beta }^{\ast }\right)\\ =b_0{\beta }^{\ast }+b_1{\beta }^{\ast }\tilde{y}\left(n\right)+b_2{\left({\beta }^{\ast }\right)}^2+b_3{\tilde{y}}^2\left(n\right)+O\left({\left(\left|\tilde{y}\left(n\right)\right|+\left|{\beta }^{\ast }\right|\right)}^3\right).\end{array}$ (4.3)

而且由(4.2)式可知

$\begin{array}{c}\tilde{x}\left(n+1\right)=\left(1-\delta \right)\tilde{x}\left(n\right)+g_1\left(\tilde{x}\left(n\right),\tilde{y}\left(n\right),{\beta }^{\ast }\right)\\ =\left(1-\delta \right)h\left(\tilde{y}\left(n\right),{\beta }^{\ast }\right)+g_1\left(h\left(\tilde{y}\left(n\right),{\beta }^{\ast }\right),\tilde{y}\left(n\right),{\beta }^{\ast }\right)\\ =\left(1-\delta \right)b_0{\beta }^{\ast }+\left[\left(1-\delta \right)b_1+\frac{\alpha \delta }{\gamma \eta +\delta }+b_0\left(\frac{\left(1-\delta \right)\alpha {\eta }^2\gamma }{\delta \left(\gamma \eta +\delta \right)}+2\alpha \eta \right)\right]{\beta }^{\ast }\tilde{y}\left(n\right)\\ +\left[\left(1-\delta \right)b_3+\alpha \eta \left(\delta -\alpha -1\right)+\frac{{\alpha }^2{\beta }^2\gamma \left(\delta -1\right)}{\delta \left(\gamma \eta +\delta \right)}\right]{\tilde{y}}^2\left(n\right)\\ +\left[\left(1-\delta \right)b_2-\eta b_0^2\right]{\left({\beta }^{\ast }\right)}^2+O\left({\left(\left|\tilde{y}\left(n\right)\right|+\left|{\beta }^{\ast }\right|\right)}^3\right).\end{array}$ (4.4)

比较(4.3)和(4.4)的系数，我们有

$b_0=0$ , $b_1=\frac{\alpha }{\gamma \eta +\delta }$ , $b_2=0$ , $b_3=\frac{\alpha \eta \left(\delta -\alpha -1\right)}{\delta }+\frac{{\alpha }^2{\eta }^2\gamma \left(\delta -1\right)}{{\delta }^2\left(\gamma \eta +\delta \right)}$ .

即 $\tilde{x}\left(n\right)=\frac{\alpha }{\gamma \eta +\delta }{\beta }^{\ast }\tilde{y}\left(n\right)+\left(\frac{\alpha \eta \left(\delta -\alpha -1\right)}{\delta }+\frac{{\alpha }^2{\eta }^2\gamma \left(\delta -1\right)}{{\delta }^2\left(\gamma \eta +\delta \right)}\right){\tilde{y}}^2\left(n\right)$ 。

限制在中心流形上的系统(4.2)可表示为

$\begin{array}{c}\tilde{y}\left(n+1\right)=\left[-\eta -\frac{\alpha {\eta }^2\gamma }{\delta \left(\gamma \eta +\delta \right)}-\frac{\eta \delta {\beta }^{\ast }}{\gamma \eta +\delta }+\frac{\alpha \gamma {\eta }^2{\beta }^{\ast }\left(1-\delta \right)}{\delta {\left(\gamma \eta +\delta \right)}^2}+\frac{\alpha \gamma {\eta }^2{\left({\beta }^{\ast }\right)}^2}{{\left(\gamma \eta +\delta \right)}^3}\right]{\tilde{y}}^2\left(n\right)\\ +\left(1+\frac{{\beta }^{\ast }\delta }{\gamma \eta +\delta }\right)\tilde{y}\left(n\right)+O\left({\left(\left|\tilde{y}\left(n\right)\right|+\left|{\beta }^{\ast }\right|\right)}^3\right).\end{array}$ (4.5)

令

$F\left(\tilde{y}\left(n\right),{\beta }^{\ast }\right)=\tilde{y}\left(n+1\right)$ ,

于是

${\frac{\partial F}{\partial \tilde{y}\left(n\right)}|}_{\left(0,0\right)}=1\ne 0$ , ${\frac{\partial F}{\partial {\beta }^{\ast }}|}_{\left(0,0\right)}=0$ , ${\frac{{\partial }^{2}F}{\partial \tilde{y}\left(n\right)\partial {\beta }^{\ast }}|}_{\left(0,0\right)}=\frac{\delta }{\gamma \eta +\delta }$ ,

${\frac{{\partial }^{2}F}{\partial {\tilde{y}}^2\left(n\right)}|}_{\left(0,0\right)}=-2\eta -2\frac{\alpha {\eta }^2\gamma }{\delta \left(\gamma \eta +\delta \right)}<0$ , ${\frac{{\partial }^{2}F}{\partial {\left({\beta }^{\ast }\right)}^2}|}_{\left(0,0\right)}=0$ .

根据文献[11]中的结论可得下列定理。

定理4.1 当参数 $\beta$ 在 $F{B}_A^1$ 的一个小邻域内变化时，系统(1.4)在点 $A\left(\frac{\delta }{\eta },0\right)$ 处发生折分支。

5. 翻转分支

由命题3.3 (3)可知，当 $\delta =2$ 和 $\beta \ne \frac{\gamma \eta }{2}+1$ 时， $A\left(\frac{\delta }{\eta },0\right)$ 处的特征值为 ${\lambda }_1=-1$ 和 ${\lambda }_2=\frac{2\beta }{\gamma \eta +2}$ 。

令 $u\left(n\right)=x\left(n\right)-\frac{a-1}{b}$ ， $v\left(n\right)=y\left(n\right)$ 和 ${\delta }^{\ast }=\delta -2$ 。在此变换下，将不动点 $A\left(\frac{\delta }{\eta },0\right)$ 转移至原点 $O\left(0,0\right)$ 研究。经过泰勒展开后，系统(1.4)转换为

$\left(\begin{array}{l}u\left(n+1\right)\\ v\left(n+1\right)\end{array}\right)=\left(\begin{array}{cc}-1& -\frac{2\alpha }{\gamma \eta +2}\\ 0& \frac{2\beta }{\gamma \eta +2}\end{array}\right)\left(\begin{array}{l}u\left(n\right)\\ v\left(n\right)\end{array}\right)+\left(\begin{array}{l}{F}_1\left(u\left(n\right),v\left(n\right),{\delta }^{\ast }\right)\\ F_2\left(u\left(n\right),v\left(n\right),{\delta }^{\ast }\right)\end{array}\right),$ (5.1)

其中 $U={\left(u\left(n\right),v\left(n\right)\right)}^T$ ，

$\begin{array}{c}{F}_1\left(u\left(n\right),v\left(n\right),{\delta }^{\ast }\right)=-{\delta }^{\ast }u\left(n\right)-\frac{\alpha \gamma \eta {\delta }^{\ast }}{\left(\gamma \eta +2\right)\left(\gamma \eta +{\delta }^{\ast }+2\right)}v\left(n\right)-\eta u^2\left(n\right)+\frac{\alpha \eta \left({\delta }^{\ast }+2\right)}{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^2}{v}^2\left(n\right)\\ -\frac{\alpha {\eta }^2\gamma }{{\left(\gamma \eta +{\delta }^{*}+2\right)}^2}u\left(n\right)v\left(n\right)-\frac{\alpha {\eta }^2\left({\delta }^{\ast }+2-\gamma \eta \right)}{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^3}u\left(n\right)v^2\left(n\right)\\ -\frac{\alpha {\eta }^2\left({\delta }^{\ast }+2\right)}{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^3}{v}^3\left(n\right)+\frac{\alpha {\eta }^3\gamma }{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^3}{u}^2\left(n\right)v\left(n\right)+O\left({\Vert U\Vert }^4\right),\end{array}$

$\begin{array}{c}{F}_2\left(u\left(n\right),v\left(n\right),{\delta }^{\ast }\right)=\frac{\beta \gamma \eta {\delta }^{\ast }}{\left(\gamma \eta +2\right)\left(\gamma \eta +{\delta }^{\ast }+2\right)}v\left(n\right)-\frac{\beta \eta \left({\delta }^{\ast }+2\right)}{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^2}{v}^2\left(n\right)-\frac{\beta {\eta }^2\gamma }{{\left(\gamma \eta +{\delta }^{*}+2\right)}^2}u\left(n\right)v\left(n\right)\\ -\frac{\beta {\eta }^2\left({\delta }^{\ast }+2-\gamma \eta \right)}{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^3}u\left(n\right)v^2\left(n\right)-\frac{\beta {\eta }^2\left({\delta }^{\ast }+2\right)}{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^3}{v}^3\left(n\right)+\frac{\beta {\eta }^3\gamma }{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^3}{u}^2\left(n\right)v\left(n\right)+O\left({\Vert U\Vert }^4\right),\end{array}$

当 $\beta \ne \frac{\gamma \eta }{2}+1$ ，我们可以构造下列可逆矩阵

$T_2=\left(\begin{array}{cc}1& -2\alpha \left(\gamma \eta +{\delta }^{\ast }+2\right)\\ 0& \left(\gamma \eta +{\delta }^{\ast }+2\right)\left(\gamma \eta +2\beta +2\right)\end{array}\right)$ .

令 $\left(\begin{array}{c}u\left(n\right)\\ v\left(n\right)\end{array}\right)=T_2\left(\begin{array}{c}\tilde{x}\left(n\right)\\ \tilde{y}\left(n\right)\end{array}\right)$ 。在此非退化变换下，将系统(5.1)转换为如下标准形式：

$\left(\begin{array}{l}\tilde{x}\left(n+1\right)\\ \tilde{y}\left(n+1\right)\end{array}\right)=\left(\begin{array}{cc}-1& 0\\ 0& \frac{2\beta }{\gamma \eta +2}\end{array}\right)\left(\begin{array}{l}\tilde{x}\left(n\right)\\ \tilde{y}\left(n\right)\end{array}\right)+\left(\begin{array}{l}{g}_1\left(\tilde{x}\left(n\right),\tilde{y}\left(n\right),{\delta }^{\ast }\right)\\ g_2\left(\tilde{x}\left(n\right),\tilde{y}\left(n\right),{\delta }^{\ast }\right)\end{array}\right),$ (5.2)

其中

$\begin{array}{c}{g}_1\left(\tilde{x}\left(n\right),\tilde{y}\left(n\right),{\delta }^{\ast }\right)=-{\delta }^{\ast }\tilde{x}\left(n\right)+\alpha {\delta }^{\ast }\left(\gamma \eta +2{\delta }^{\ast }+4\right)\tilde{y}\left(n\right)-\eta {\tilde{x}}^2\left(n\right)-2{\alpha }^2\gamma {\eta }^2\left(\gamma \eta +6+4{\delta }^{\ast }\right){\tilde{y}}^2\left(n\right)\\ +\left[4\alpha \eta \left(\gamma \eta +{\delta }^{\ast }+2\right)-\frac{\alpha {\eta }^2\gamma \left(\gamma \eta +2\right)}{\gamma \eta +{\delta }^{\ast }+2}\right]\tilde{x}\left(n\right)\tilde{y}\left(n\right)\\ +\alpha \eta \left({\delta }^{\ast }+2\right)\left(\left(1-2\beta \right)\left(\gamma \eta +2\beta +2\right)-4\alpha \left({\delta }^{\ast }+2\right)\right){\tilde{y}}^2\left(n\right)\\ +\frac{\alpha {\eta }^2\left(2\beta -1\right)\left({\delta }^{\ast }+2-\gamma \eta \right)\left(\gamma \eta +2\beta +2\right)}{\gamma \eta +{\delta }^{\ast }+2}\tilde{x}\left(n\right){\tilde{y}}^2\left(n\right)\\ -\frac{4{\alpha }^2{\eta }^3\gamma \left(\gamma \eta +2\right)}{\gamma \eta +{\delta }^{\ast }+2}\tilde{x}\left(n\right){\tilde{y}}^2\left(n\right)+\frac{\alpha {\eta }^3\gamma \left(\gamma \eta +2\right)}{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^2}{\tilde{x}}^2\left(n\right)\tilde{y}(\; n\; )\end{array}$

$\begin{array}{c}+\left[4{\alpha }^3{\eta }^3\gamma \left(\gamma \eta +2\right)-\alpha {\eta }^2\left(\gamma \eta +2\right)\left({\delta }^{\ast }+2\right){\left(\gamma \eta +2\beta +2\right)}^2\right]{\tilde{y}}^3\left(n\right)\\ +2{\alpha }^2{\eta }^2\left(1-2\beta \right)\left({\delta }^{\ast }+2-\gamma \eta \right)\left(\gamma \eta +2\beta +2\right){\tilde{y}}^3\left(n\right),\end{array}$

$\begin{array}{c}{g}_2\left(\tilde{x}\left(n\right),\tilde{y}\left(n\right),{\delta }^{\ast }\right)=\frac{\beta \eta \gamma {\delta }^{\ast }}{\left(\gamma \eta +2\right)\left(\gamma \eta +{\delta }^{\ast }+2\right)}\tilde{y}\left(n\right)+\frac{\beta \eta \left[2\alpha \gamma \eta -\left({\delta }^{\ast }+2\right)\left(\gamma \eta +2\beta +2\right)\right]}{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^2}{\tilde{y}}^2\left(n\right)\\ +\frac{\beta {\eta }^2\gamma }{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^2}\tilde{x}\left(n\right)\tilde{y}\left(n\right)-\frac{\beta {\eta }^3\gamma }{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^3}{\tilde{x}}^2\left(n\right)\tilde{y}\left(n\right)\\ +\frac{\beta {\eta }^2\left[4\alpha \gamma \eta +\left({\delta }^{\ast }+2-\gamma \eta \right)\left(\gamma \eta +2\beta +2\right)\right]}{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^2}\tilde{x}\left(n\right){\tilde{y}}^2\left(n\right)\\ +\frac{\beta {\eta }^2\left(\gamma \eta +2\beta +2\right)\left[2\alpha \gamma \eta +\left({\delta }^{\ast }+2\right)\left(\gamma \eta +2\beta -2\alpha +2\right)\right]-4{\alpha }^2\beta {\eta }^3\gamma }{\gamma \eta +{\delta }^{\ast }+2}{\tilde{y}}^3\left(n\right),\end{array}$

通过中心流形定理和文献 [1] 的方法可知，在原点处 ${\delta }^{\ast }=0$ 的小邻域内存在系统(5.2)的中心流形 $M^c\left(0\right)$ ，其近似表示如下：

$M^c\left(0\right)=\left\{\left(\tilde{x}\left(n\right),\tilde{y}\left(n\right),{\delta }^{\ast }\right)\in R^3|\tilde{y}\left(n\right)=h\left(\tilde{x}\left(n\right),{\delta }^{\ast }\right),h\left(0,0\right)=0,Dh\left(0,0\right)=0\right\}$ .

对所有充分小的 $\tilde{x}\left(n\right)$ 和 ${\delta }^{\ast }$ ，假设中心流形的形式为

$h\left(\tilde{x}\left(n\right),{\delta }^{\ast }\right)=b_0{\delta }^{\ast }+b_1{\delta }^{\ast }\tilde{x}\left(n\right)+b_2{\left({\delta }^{\ast }\right)}^2+b_3{\tilde{x}}^2\left(n\right)+O\left({\left(\left|\tilde{x}\left(n\right)\right|+\left|{\delta }^{\ast }\right|\right)}^3\right)$ ,

其中 $O\left({\left(\left|\tilde{x}\left(n\right)\right|+\left|{\delta }^{\ast }\right|\right)}^3\right)$ 是一个至少有三个变量阶的函数。下面我们通过待定系数法求出系数 $b_i\left(i=0,1,2,3\right)$ ，由中心流形的近似表示可知

$\begin{array}{c}\tilde{y}\left(n+1\right)=h\left(\tilde{x}\left(n+1\right),{\delta }^{\ast }\right)\\ =b_0{\delta }^{\ast }-b_1{\delta }^{\ast }\tilde{x}\left(n\right)+b_2{\left({\delta }^{\ast }\right)}^2+b_3{\tilde{x}}^2\left(n\right)+O\left({\left(\left|\tilde{x}\left(n\right)\right|+\left|{\delta }^{\ast }\right|\right)}^3\right).\end{array}$ (5.3)

而且由(5.2)式可知

$\begin{array}{c}\tilde{y}\left(n+1\right)=\frac{2\beta }{\gamma \eta +2}\tilde{y}\left(n\right)+g_1\left(\tilde{x}\left(n\right),\tilde{y}\left(n\right),{\delta }^{\ast }\right)\\ =\frac{2\beta }{\gamma \eta +2}h\left(\tilde{x}\left(n\right),{\delta }^{\ast }\right)+g_1\left(\tilde{x}\left(n\right),h\left(\tilde{x}\left(n\right),{\delta }^{\ast }\right),{\delta }^{\ast }\right)\\ =\frac{2\beta }{\gamma \eta +2}{b}_0{\delta }^{\ast }+\left(\frac{2\beta }{\gamma \eta +2}{b}_1+\frac{b_0\beta {\eta }^2\gamma }{{\left(\gamma \eta +{\delta }^{\ast }+2\right)}^2}\right){\delta }^{\ast }\tilde{x}\left(n\right)+\frac{2\beta }{\gamma \eta +2}{b}_3{\tilde{x}}^2\left(n\right)\\ +\left(\frac{2\beta }{\gamma \eta +2}{b}_2+\frac{b_0\beta \eta \gamma }{\left(\gamma \eta +2\right)\left(\gamma \eta +{\delta }^{\ast }+2\right)}\right){\left({\delta }^{\ast }\right)}^2\\ +\frac{b_0^2\beta \eta \left[2\alpha \gamma \eta -\left({\delta }^{\ast }+2\right)\left(\gamma \eta +2\beta +2\right)\right]}{\gamma \eta +{\delta }^{\ast }+2}{\left({\delta }^{\ast }\right)}^2+O\left({\left(\left|\tilde{x}\left(n\right)\right|+\left|{\delta }^{\ast }\right|\right)}^3\right).\end{array}$ (5.4)

比较(5.3)和(5.4)的系数，我们有

$b_0=0$ , $b_1=0$ , $b_2=0$ , $b_3=0$ .

即 $\tilde{y}\left(n\right)=0$ 。则限制在中心流形上的系统(5.2)可表示为

$\tilde{x}\left(n+1\right)=-\tilde{x}\left(n\right)-{\delta }^{\ast }\tilde{x}\left(n\right)-\eta {\tilde{x}}^2\left(n\right)+O\left({\left(\left|\tilde{x}\left(n\right)\right|+\left|{\delta }^{\ast }\right|\right)}^3\right).$ (5.5)

令

$F\left(\tilde{x}\left(n\right),{\delta }^{\ast }\right)=\tilde{x}\left(n+1\right)$ ,

于是

$F\left(0,0\right)=0$ , ${\frac{\partial F}{\partial \tilde{x}\left(n\right)}|}_{\left(0,0\right)}=-1$ ,

$\alpha ={\left(\frac{{\partial }^{2}F}{\partial \tilde{x}\left(n\right)\partial {\delta }^{\ast }}+\frac{1}{2}\frac{\partial F}{\partial {\delta }^{\ast }}\frac{{\partial }^{2}F}{\partial {\tilde{x}}^2\left(n\right)}\right)|}_{\left(0,0\right)}=-1\ne 0$ ,

$\beta ={\left[\frac{1}{6}\frac{{\partial }^{3}F}{\partial {\tilde{x}}^3\left(n\right)}+{\left(\frac{1}{2}\frac{{\partial }^{2}F}{\partial {\tilde{x}}^2\left(n\right)}\right)}^2\right]|}_{\left(0,0\right)}={\eta }^2>0$ .

根据文献 [11] 中的结论可得下列定理。

定理5.1当参数 $\delta$ 在 $F{B}_A^2$ 的一个小邻域内变化时，系统(1.4)在点 $A\left(\frac{\delta }{\eta },0\right)$ 处发生翻转分支。

6. 数值模拟

在本节中，我们使用系统(1.4)的分支图和最大李雅普诺夫指数图来验证上述分析结果。接下来考虑以下两种情况下的分支参数。

情形1. 假设系统(1.4)中的参数 $\alpha =1$ ， $\delta =1$ ， $\eta =1$ 和 $\gamma =1$ 。我们发现，当 $\beta =\frac{\gamma \eta }{\delta }+1=2$ 时，在不动

(a)(b)

Figure 1. (a) Bifurcation diagram of the system (1.4) in $\left(\beta ,x\right)$ -plane when $\alpha =1$ , $\delta =1$ , $\eta =1$ , $\gamma =1$ and $\beta$ varies in [1,3], the initial value is (0.9,0.1). (b) Bifurcation diagram of the system (1.4) in $\left(\beta ,y\right)$ -plane with same parameters in (a)

图1. (a) 当 $\alpha =1$ ， $\delta =1$ ， $\eta =1$ ， $\gamma =1$ ， $\beta$ 在[1,3]范围内变化时，系统(1.4)的 $\left(\beta ,x\right)$ -平面分支图，初始值为(0.9,0.1)。(b) 系统(1.4)在(a)中相同参数的条件下的 $\left(\beta ,y\right)$ -平面分支图

点 $\left(\frac{\delta }{\eta },0\right)$ 处出现了折分支。这证实了定理4.1。

图1为系统(1.4)的分支图。可以看出，当 $1<\beta \le 2$ 时，不动点 $A\left(1,0\right)$ 在中心流形上是稳定的。当 $\beta >2$ 时，中心流形上的定点 $A\left(1,0\right)$ 变得不稳定。因此，跨临界类型的折分支发生了。

情形2. 假设系统(1.4)中的参数 $\alpha =1$ ， $\beta =1$ ， $\eta =1$ 和 $\gamma =1$ 。我们发现，当 $\delta =2$ 时，在不动点 $\left(2,0\right)$ 处出现了翻转分支。这证实了定理5.1。

图2(a)为系统(1.4)的分支图。可以看出，当 $\delta <2$ 时，不动点 $A\left(\delta ,0\right)$ 在中心流形上是稳定的。当 $\delta =2$ 时，系统(1.4)在不动点 $A\left(\delta ,0\right)$ 处发生跨临界翻转分支。当 $\delta$ 增加到2.6时，系统(1.4)发生逆周期加倍分支。因此，在不动点 $A\left(\delta ,0\right)$ 附近的系统(1.4)是具有窄周期窗口的混沌系统。图2(a)对应的最大Lyapunov指数计算在图2(b)中。

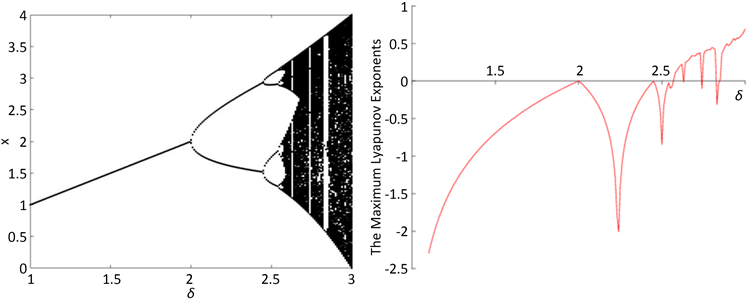(a)(b)

Figure 2. (a) Bifurcation diagram of the system (1.4) in $\left(\delta ,x\right)$ -plane when $\alpha =1$ , $\beta =1$ , $\eta =1$ , $\gamma =1$ and $\delta$ varies in [1.1,3], the initial value is (1.9,0.1). (b) Maximum Lyapunov exponents corresponding to (a)

图2. (a) 当 $\alpha =1$ ， $\beta =1$ ， $\eta =1$ ， $\gamma =1$ 时， $\delta$ 在[1.1, 3]范围内变化时，系统(1.4)的 $\left(\delta ,x\right)$ -平面分支图，初始值为(1.9, 0.1)。(b) (a)对应的最大李雅普诺夫指数图

7. 总结与展望

本文在 ${ℝ}^{+}$ 空间内建立了一个具有Beddington-DeAngelis型功能反应的离散捕食者–食饵模型。我们得到了系统(1.4)的平衡点及其存在的条件。利用中心流形定理和分支理论，证明了系统(1.4)的边界平衡点可以发生翻转分支和折分支。系统(1.4)表现出倍周期级联，周期窗口较窄的混沌和周期为2的轨道等有趣的动力学行为，这意味着系统(1.4)的边界平衡点通过分支而失去稳定性。然而，正平衡点的分支问题尚未讨论。如何设置合理的参数对正平衡点上的分支进行分析是进一步研究的课题。