交叉验证法在模型比较中的应用

Application of Cross-Validation in Model Comparison

摘要: 在模型比较中，有很多评价标准，如p-值等，都受制于数据的分布假定。而利用交叉验证法进行数据处理，然后比较归一化均方误差Normalized Mean Squared Error (NMSE)是目前最流行的模型评价的标准，不受任何数据分布的限制。本文详细介绍了交叉验证法，并给出了其具体的应用。通过对实际的问题建立了6种不同的模型，并利用10折交叉验证法对不同模型的归一化均方误差(NMSE)进行比较，选择出了最优的预测精度最高的模型。

Abstract: In model comparison, there are many evaluation criteria, such as p-value, which are subject to the distribution assumptions of the data. The use of cross-validation method for data processing and then comparison of normalized mean squared error (NMSE) is currently the most popular standard for model evaluation, which is not limited by any data distribution. This article introduces the cross-validation method in detail and gives its specific application. By establishing six different models for the actual problem, and comparing the normalized mean squared error (NMSE) of dif-ferent models by using the 10-fold cross-validation method, the optimal model with the highest prediction accuracy was selected.

1. 引言

随着互联网技术的发展，机器学习愈发火热，在对一个实例进行分析时，我们可以应用不同的模型来处理数据，最终选择哪一种模型去应用，成为了我们解决问题的关键。利用交叉验证法处理数据，并比较归一化均方误差(NMSE)是目前机器学习中最流行的选择模型的标准。本文采用R语言程序，分析气缸数、排量、马力、重量、型号等因素对汽车油耗的影响，利用10折交叉验证法，去比较6种模型的优劣，根据预测精度–归一化均方误差(NMSE)的大小，选择出最优的模型。

2. 交叉验证法

在机器学习中，我们需要通过实验测试来对不同模型(学习器)的泛化误差进行比较。因此，需要一个测试集，根据测试集上的测试误差来判别模型对新样本的判别能力，即模型的好坏。测试样本要求从样本真实分布中独立同分布得到，并且尽可能的与训练集互斥。假定我们的数据集为 $D=\left\{\left(x_1,y_1\right),\cdots ,\left(x_m,y_m\right)\right\}$ [1] ，一般需要对数据集D进行恰当的处理，产生训练集S和测试集T。

交叉验证法是机器学习中最常用的实验评估方法。下面以K折交叉验证为例，说明交叉验证的具体实验过程。K折交叉验证即把数据集D划分成K个数据量大小相似的互斥子集，并且要求这些子集的数据分布尽量保持一致。然后先用K − 1份子集做为训练模型的训练集，剩下一份子集用来做测试集，这样我们就得到了K对训练集和测试集 [2] 。

利用训练集训练出来的模型对测试集进行模型评估后，计算这K个测试集的均方误差(MSE)：

$\text{MSE}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-{\hat{y}}_i\right)}^2}$

其中测试集中样本量为n， $y_i$ 为测试集中的样本值， ${\hat{y}}_i$ 是训练模型得到的值。对这K个MSE求均值即MeanMSE，显然MeanMSE越小，模型拟合的越好。因此以MeanMSE的值作为标准来判断模型的好坏 [3] 。

一般在做交叉验证时，我们可以发现，随着数据集划分的方式不同，我们做交叉验证的结果也会不同，因此还要对上述K折交叉验证再重复几次，而且每一次用不同的方式划分数据集。例如做5次10折交叉验证，再求出它们的均值，这样消除了大部分偶然的误差情况，使因划分方式的不同带来的结果差异得到减小，使得模型测试结果更加客观。K折交叉验证法有着避免过拟合和欠拟合的优势。但是K值的最佳选取是它的最大问题 [4] 。

另一种常见的交叉验证法，是留一法，它是K折交叉验证的另一种形式。如果样本数据量为n，那么此时令K = n，即每一份数据只有一个样本数据，在某些情况下它相较于K折交叉验证更加精确，因为留一法不用考虑样本数据随机划分的影响，而且留一法所采用的训练集只比原始样本集少一个数据。然而留一法也有一个很明显的缺陷，当样本数据集的个数很大时，训练n个模型的速度与效率大大降低，计算成本也随着样本数据量的增大而增大，从而多了更多的麻烦。

3. 实例分析

汽车的油耗和车型、马力、排量等有关，下面我们以一组实验数据为例，训练不同的学习模型，探讨汽车油耗和各种因素之间的关系。本文的实验数据是一组汽车的油耗数据，其中，mpg (耗油量：每加仑英里数)为因变量，自变量有cylinders (气缸数)、displacement (排量)、horsepower (马力)、weight (重量)、acceleration (加速)、model.year (型号年)、origin (来源：3个之一) [5] ，本实例的部分数据见表1。

Table 1. Car fuel consumption data

表1. 汽车油耗数据

我们对汽车油耗数据分别建立了决策树模型、线性回归模型、bagging回归、随机森林模型、mboost模型、支持向量机模型，使用R语言程序，采用10折交叉验证法对数据进行处理，根据预测精度来评估以上模型的好坏。评估标准采用NMSE即归一化均方误差，NMSE的表达式为：

$\text{NMSE}=\frac{1}{M}\text{MSE}$

其中 $M=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-\bar{y}\right)}^2}$ ， $\bar{y}$ 为测试集中因变量的样本均值，n为测试集中样本量， $y_i$ 为测试集中因变量的样本值 [6] 。

在进行交叉验证时，关键在于对数据进行分组。由于第8个变量origin是分类变量，我们分组时需要在其3个水平中进行平衡。下面是数据分析中我们编制的分组函数FOLD()。

Fold=function(10,w,8,seed=8888){# w是用到的数据集

n=nrow(w);d=1:n;dd=list()

e=levels(w[,8]);T=length(e)#定性变量origin共T类

set.seed(seed)

for(i in 1:T){

d0=d[w[,8]==e[i]];j=length(d0)

ZT=rep(1:10,ceiling(j/10))[1:j]

id=cbind(sample(ZT,length(ZT)),d0);dd[[i]]=id}

#上面每个dd[[i]]是随机1:10及第i类的下标集组成的矩阵

mm=list()

for(i in 1:10){u=NULL;

for(j in 1:T)u=c(u,dd[[j]][dd[[j]][,1]==i,2])

mm[[i]]=u} #mm[[i]]为第i个下标集i=1,...,10

return(mm)} #输出10个下标集

我们进行了1次10折交叉验证，最终得到6种模型的NMSE结果见表2，通过结果可以看出，对于汽车油耗这个实际问题，预测效果最好的是支持向量机模型，它的平均标准化均方误差最小，其次是随机森林与mboost模型，再然后是bagging模型与传统的线性回归，拟合效果最差的模型是回归树模型。

Table 2. 10-fold cross-validated NMSE for 6 models

表2. 6种模型的10折交叉验证的NMSE

其中Tree代表决策树模型，lm代表线性回归模型，bagging为bagging回归，RF是随机森林模型，boost是mboost模型，SVM是支持向量机模型。

折线图结果见图1，柱形图结果见图2。

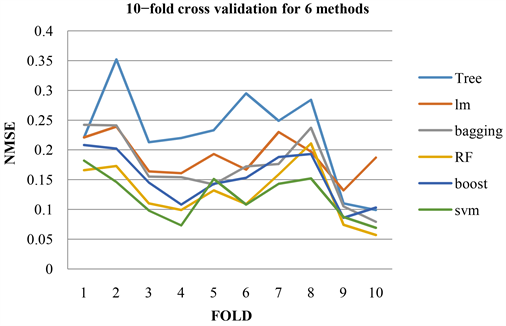
Figure 1. 10-fold cross-validated NMSE for 6 models

图1. 6种模型的10折交叉验证的NMSE

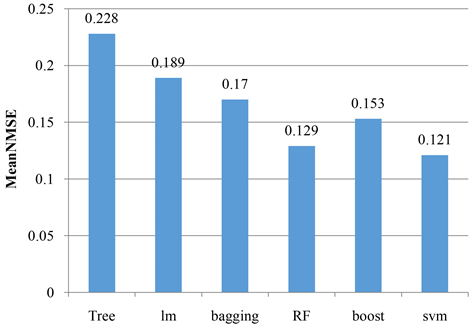
Figure 2. 10-fold cross-validated mean NMSE for 6 models

图2. 6种模型的10折交叉验证的平均NMSE

4. 结论

从上述实例分析结果可以看到，数学上非常精密的线性回归模型在数据预测精度上并不是最好的，机器学习方法中比较流行的回归树模型预测精度也不好。模型的好坏不能由数据分布的假定来决定，比如完全依赖于数据分布的线性回归模型，也不能由模型的复杂度来决定，比如比较简单的回归树模型。根据预测精度对模型好坏进行评判的交叉验证法是比较客观的判断方法，因为其完全根据数据本身来决定模型的好坏，并且通过使用10折交叉验证法计算每个模型的平均NMSE，可以直接判断出解决此问题的最佳模型，并对每一个模型的精度进行了直观的比较与区分。

附录

程序：

w=read.csv(auto.mpg.csv)

w[,8]=factor(w[,8])

library(missForest)

w=missForest(w[,-9])$ximp

#读取数据集，使第8个变量因子化，并删除数据第9列汽车名字。

Fold=function(Z,w,D,seed=8888){

n=nrow(w);d=1:n;dd=list()

e=levels(w[,8]);T=length(e)#origin有T类

set.seed(seed)

for(i in 1:T){

d0=d[w[,D]==e[i]];j=length(d0)

ZT=rep(1:Z,ceiling(j/Z))[1:j]

id=cbind(sample(ZT,length(ZT)),d0);dd[[i]]=id}

#上面每个dd[[i]]是随机1:Z及i类的下标集组成的矩阵

mm=list()

for(i in 1:Z){u=NULL;

for(j in 1:T)u=c(u,dd[[j]][dd[[j]][,1]==i,2])

mm[[i]]=u} #mm[[i]]为第i个下标集i=1,...,Z

return(mm)}#输出Z个下标集

#构建FOLD函数对数据集进行交叉验证的分折

library(rpart); #回归树

library(ipred); #bagging

library(mboost); #mboost

library(randomForest); #随机森林

library(kernlab) #svm

library(e1071); #svm

#加载各个模型所需的程序包

C=1;Z=10

mm=Fold(10,w,8,8888);gg=mpg~.

gg1=mpg~btree(cylinders)+btree(displacement)+btree(horsepower)+btree(weight)+

btree(acceleration)+btree(model.year)+btree(origin)

MSE=matrix(99,Z,6)->NMSE;

#构建回归方程，其中gg1代表应用mboost模型时的回归方程，采用btree学习器，每个变量对一颗决策树。

J=1;for(i in 1:Z)

{m=mm[[i]];M=mean((w[m,C]-mean(w[m,C]))^2);a=rpart(gg,w[-m,])

MSE[i,J]=mean((w[m,C]-predict(a,w[m,]))^2)

NMSE[i,J]=MSE[i,J]/M};

#决策树模型的NMSE

J=J+1;for(i in 1:Z)

{m=mm[[i]];M=mean((w[m,C]-mean(w[m,C]))^2);a=lm(gg,w[-m,])

MSE[i,J]=mean((w[m,C]-predict(a,w[m,]))^2)

NMSE[i,J]=MSE[i,J]/M};

#线性回归的NMSE

J=J+1;set.seed(1010)

for(i in 1:Z)

{m=mm[[i]];M=mean((w[m,C]-mean(w[m,C]))^2);a=bagging(gg,w[-m,])

MSE[i,J]=mean((w[m,C]-predict(a,w[m,]))^2)

NMSE[i,J]=MSE[i,J]/M};

#bagging模型的NMSE

J=J+1;set.seed(1010)

for(i in 1:Z)

{m=mm[[i]];M=mean((w[m,C]-mean(w[m,C]))^2);a=randomForest(gg,w[-m,])

MSE[i,J]=mean((w[m,C]-predict(a,w[m,]))^2)

NMSE[i,J]=MSE[i,J]/M};

#随机森林模型的NMSE

J=J+1;set.seed(1010)

for(i in 1:Z)

{m=mm[[i]];M=mean((w[m,C]-mean(w[m,C]))^2)

a=mboost(gg1,w[-m,])

MSE[i,J]=mean((w[m,C]-predict(a,w[m,]))^2)

NMSE[i,J]=MSE[i,J]/M};

#mboost模型的NMSE

J=J+1;set.seed(1010);

for(i in 1:Z)

{m=mm[[i]];M=mean((w[m,C]-mean(w[m,C]))^2)

a=svm(gg,w[-m,])

MSE[i,J]=mean((w[m,C]-predict(a,w[m,]))^2)

NMSE[i,J]=MSE[i,J]/M};

#支持向量机模型的NMSE

NMSE=data.frame(NMSE)

names(NMSE)=c(TreelmbaggingRFboostsvm)

(MNMSE=apply(NMSE,2,mean))

#输出10折交叉验证的平均NMSE，单独输出NMSE可得到交叉验证每一折的NMSE

NOTES

^*通讯作者。