1. 引言
在时间序列模型的建模分析过程中,诊断检验是非常重要的一步,具体体现在检验拟合模型的残差序列是否存在自相关。
假设时间序列
由平稳可逆的自回归移动平均模型ARMA(p,q)生成,具体公式为:
(1)
其中
、
,L为滞后算子,
。则
为估计值,许多诊断检验方法的提出基于残差的自相关系数,
(2)
其中
。
最初,Box和Pierce (1970) [1] 用残差的自相关系数构造了如下统计量:
(3)
m是选取的残差自相关系数的个数。在残差序列是白噪声序列(
)的原假设下,Q近似服从自由度为m的
分布。使用这个统计量,明显可以发现较多的残差自相关系数将导致较大的Q值。Ljung和Box (1978) [2] 在研究中提出了更优且对小样本同样适用的修正的Q统计量,它的结构如下:
(4)
在原假设条件下,
近似服从自由度为m-p-q的
分布。
Ljung-Box检验(简记为L-B检验)自提出以来被广泛应用于实证研究中,但是,一些学者在后续的研究过程中发现L-B检验本身存在局限性并在实际检验中表现不佳,例如Mcleod (1978) [3] 证明其统计量的卡方渐近分布依赖于某种特定的线性形式;Lee (2016) [4] 发现对于波动性建模,由于条件方差的存在会使L-B检验的实际检验水平发生严重扭曲。对于此类针对模型结识别果的检验过程,如果在检验上出现偏差,就很有可能造成模型识别错误,进而影响后续对实证问题的分析与研究。因此,实证工作者应提起注意。
由于L-B检验容易理解且大多数统计软件都提供了该统计量的计算结果,使得有关时间序列分析的实证研究过分依赖于L-B检验。但是,随着理论研究的进展,基于L-B检验所发展出来的新的检验不断被提出,并且在计算和使用上也比较便利。本文选取的四种基于L-B检验的改进方法,包括Monti检验、Mahdi-Mcleod检验以及Fisher和Gallagher提出的两种检验方法。它们基于残差的自相关系数或偏相关系数构建检验统计量。从计算方面来说,这两种相关系数均可以在常用的统计软件中提取,改进方法不需要进行额外的计算;从有限样本的渐近分布来看,新的检验统计量都服从常用分布,也不需要重新计算检验的临界值。
此外,L-B检验以及本文选取的四种改进方法中,都需要自行设定m的取值。针对这一问题,Ljung (1986) [5] 提出对于常用的时间序列m = 5较为合适。Battaglia (1990) [6] 研究了m对L-B检验的影响,提出
更为合适。Hyndman (2014) [7] 从残差自相关系数中包含的信息的角度出发,认为m应该足够大,并提出对于非季节性时间序列
,对于季节性时间序列
,h为季节性滞后。Hassani和Yeganegi (2019) [8] 从理论上证明了m的选取会对检验造成影响。此后,Hassani和Yeganegi (2020) [9] 进一步在先满足实际检验水平不高于名义检验水平的前提下,研究使检验功效尽可能大的m的取值,得出在样本容量低于500时,m取3。分析以上m的取值建议可以发现,各位学者都考虑了小样本情况的m的选取问题。但是在其文章和其他的相关研究的模拟实验中,小样本情况并没有被充分的考虑到。针对m的取值,本文考虑到相关研究的常用取值方法,以及不同样本量应取不同值,本文选择Battaglia (1990) [6] 的方法。
综上,本文着重研究有限样本条件下,各个检验方法的性能。样本大小的界定按照常规的界定方法,N ≤ 30为小样本,N > 30为大样本。首先,使用蒙特卡罗模拟实验法,从检验功效与实际检验水平的角度对其进行比较分析,筛选检验效果更佳的检验方法,为实证工作提供参考;其次,从实际检验水平的角度研究小样本情况下各检验方法对m的敏感性;最后,进行总结性阐述。文章安排如下,第二部分简单介绍了四种改进方法的检验统计量推导过程和对应的分布函数。第三部分利用蒙特卡罗模拟的方法,在有限样本的情况下,对五种检验统计量的实际检验水平进行了对比研究;同时研究了小样本情况下,不同m对实际检验水平的影响;并对模拟的异常情况进行了分析与解释。第四部分模拟了有限样本条件下,各个检验统计量的检验功效。第五部分进行总结。
2. 四种基于L-B检验的改进方法的介绍
2.1. Monti检验
Monti (1994) [10] 提出用残差的偏自相关系数代替自相关系数。两种相关系数大同小异,在计算相关性时偏自相关系数移除了中间变量的间接影响。如果残差项为白噪声过程,则残差的偏自相关系数应与零没有显著差异。因此模型拟合的充分性检验可与基于统计量:
(5)
令
,
。通过Durbin-Levinson算法,向量
可以用
的函数表示,
,对于第k个元素而言:
(6)
其中,
是k × k的托普利茨矩阵,
,
。
是m个残差偏自相关系数组成的向量,然后将式(6)中的误差的偏自相关系数替换为残差的偏自相关系数就可以得到
,对于残差的滞后k阶的偏自相关系数就是指剔除了中间k − 1残差项的干扰后,
对
影响的相关度量。Monit证明了
的近似分布为均值为0,方差为
。进而
服从自由度为
的卡方分布。
2.2. Mahdi-Mcleod检验
Mahdi和Mcleod (2012) [11] 在将Pena和Rodriguez (2002, 2006) [12] [13] 提出的检验方法拓展至多元时间序列模型的同时,对其在单变量时间序列模型下的检验统计量进行了修正。
Pena和Rodriguez (2002) [12] 指出估计的残差可以被认为是来自某个分布的多元数据的样本。在多元分析中,检验一组正态随机变量是否具有标量协方差矩阵的似然比检验与多元变量相关矩阵的行列式成正比。对于平稳的时间序列,m阶的残差相关矩阵可以表示为:
(7)
残差自相关的检验统计量可以由
的一种转换形式构造,这样可以获得在零假设下更简单的分布形式。检验统计量结构如下:
(8)
该统计量近似服从伽马分布,为了使该统计量的分布更加近似于伽马分布,将矩阵中的每个自相关系数进行了标准化,
。得到新的检验统计量:
(9)
后续的研究中Lin和Mcleod (2006) [14] 强调了自相关系数矩阵
是非负定的,但将其中的自相关系数标准化后,新的矩阵
不一定是非负定的。而且根据Pena和Rodriguez (2002) [12] 得到的统计数据经常是无定义的,他们建议使用蒙特卡洛模拟构造分布的临界值。虽然,这将会使检验过程更加复杂。
该统计量的一种理解可以是式(7)的递归表达式,如果定义
,则
。利用分块矩阵行列式的性质:
,其中
是残差的多重相关系数的平方。通过多次重复使用这个性质,可以得到:
(10)
是依赖性的一种度量,
是这些度量的几何平均值。因此
可以解释为平均的平方相关系数。再根据方差分析中残差平方和的性质可以得到,
(11)
式(10)和式(11)联立可解得:
(12)
Mahdi和Mcleod (2012) [11] 提出了自相关系数的托普利茨矩阵的行列式的对数形式,利用式(12)的结果,提出检验统计量:
(13)
使用近似于Pena和Rodriguez (2002, 2006) [12] [13] 中的方法以及Box (1954) [15] 的一个重要结果,他们证明了Qmm的领分布近似为自由为
的卡方分布。
2.3. Fisher-Gallagher检验
Fisher和Gallagher (2012) [16] 利用高维数据分析的思想,推导出新的基于m阶自相关矩阵的迹的平方的组合检验。
假设
表示矩阵
的概率极限,为了检验独立同分布的相关结构,检验H0:
,这等价于检验
中的每一个特征值是否为1。在实践中,可以使用矩阵
和它的特征值
检验H0。似然比准则使用特征值的几何平均值。如果矩阵
是奇异或接近奇异的,则可以提出基于特征值的算术平均值的统计量,其中需注意
,通过一些代数转化,可以等价为:
。再通过计算矩阵
的迹,可以考虑基于不等式
对假设进行检验。
不等式两边同乘
,再对残差的自相关系数进行标准化,可以得到统计量:
(14)
该统计量可以理解为一个加权的Ljung-box统计量,滞后1期的残差自相关系数的权重为1,滞后m期的权重为1/m。使用残差的偏自相关系数进行类似的推导,可以得到一个加权的Monit统计量:
(15)
为了便于计算,使用与Pena和Rodriguez (2002) [12] 相同的理论与方法,得到统计量的近似分布为伽马分布,shape和scale参数分别为:
(16)
(17)
通过介绍可以看出,QMT与QLB在零假设的条件下,是渐近等价的,但因为相关系数的选择不同,它们在小样本下的表现会不同;QMM的渐近分布具有比较保守的自由度,这会使它不容易犯第一种错误;QWLB和QWMT是给QLB和QMT加上了权重,滞后期较前的相关系数权重较大,随着滞后期的增加,同期的残差自相关系数的权重越小。本文主要研究有限样本下的各检验方法的性能,具体四种改进方法的优劣,在下文中进行模拟分析。
3. 有限样本下的实际检验水平的模拟研究与结果分析
实际检验水平就是犯第一类错误的概率。通过蒙特卡罗模拟的方法,在原假设的基础上模拟生成数据,之后进行检验,重复多次,拒绝原假设的概率就是实际检验水平。Davidson和MacKinnon (1999) [17] 介绍了另一种与实际检验水平有关的方法是水平扭曲,它指实际检验水平与名义检验水平的差值,用来刻度极限样本分布能否更好的近似于有限样本分布。
接下来,本文将对
和
(分别对应公式(4)、式(5)、式(13)、式(14)、式(15))四种检验方法的实际检验水平与检验功效进行研究。在本章的模拟实验中,重复生成1000个时间序列,其中样本量考虑了N=20、30、50、80、100、500六种情况,
(选取近似的整数值)。
实际检验水平的蒙特卡罗模拟实验的具体步骤为:
1) 生成数据:以AR(1)模型
作为数据生成过程,生成时间序列数据。其中考虑到系数对模拟结果的影响,借鉴Pena和Rodriguez (2002) [12] 中的模型,
取0.1、0.3、0.5、0.7、0.9;
2) 拟合模型:用生成的数据再次拟合AR(1)模型;
3) 进行检验:用五种不同的方法在给定显著性水平α = 0.05的条件下,对残差序列进行自相关检验;
4) 重复实验:将步骤1~3重复1000次,计算拒绝原假设的概率。
3.1. 有限样本下的实际检验水平的模拟
表1展示了不同的有限样本下,基于AR(1)模型的实际检验水平的模拟结果。采用Battaglia (1990) [6] 中m的取值方法,针对不同的N = 20、30、50、80、100、500,m = 4、5、7、9、10、22。
在φ = 0.9的模型中,N = 20、30时,实际检验水平过大;N = 50时各检验统计量的实际检验水平都大于0.05。原因可能为在模型估计的系数越接近1时,估计越容易出现问题,进而模拟结果出现异常。本节的结果分析中,先抛开此三种情形,后续单独对异常情况进行分析和解释。

Table 1. Actual test level of five test methods based on AR (1) model with limited samples (α = 0.05)
表1. 基于AR(1)模型的有限样本下五种检验方法的实际检验水平模拟分析(α = 0.05)
注:实际检验水平超过0.05的加粗表示。
从实际检验水平的角度分析。1) QMT统计量的实际检验水平在样本量N = 20、30、50、80时的表现差于QLB,经常超过名义检验水平。随着样本容量的增加,表现逐渐变好;2) QMM统计量的实际检验水平相对比较保守,全部低于实际检验水平,且多数低于其他检验统计量;3) QLB统计量的实际检验水平在不同的样本量的情况下,都会出现大于名义检验水平的情况。然而,QWLB和QWMT统计量的实际检验水平全部低于且接近名义检验水平。这表明,QWLB和QWMT统计量与QLB相比,有限样本分布更好的近似于渐近分布,且在使用时能更少的犯“弃真”的错误;4) 在去除掉异常情况的前提下,QLB统计量实际检验水平的范围是0.026~0.064,对比来看,QWLB和QWMT统计量的范围分别是0.031~0.050和0.33~0.48,后两者更加稳定。从水平扭曲的角度分析。表2展示了去除掉所有φ = 0.9的模拟结果后,各样本容量下五种检验统计量的平均水平扭曲程度,该值是在每一个样本中,将所有模型的水平扭曲值简单平均得到。结果显示,QMM统计量的水平扭曲程度较大,五种样本容量下的平均水平扭曲程度超过0.015,即在有限样本下,使用QMM统计量进行残差自相关检验时,更有可能产生错误的结论。QMT统计量在N = 20时,扭曲程度较大。除此之外、QLB、QWLB和QWMT统计量的平均水平扭曲程度全部小于0.015,即从此角度分析,三种检验统计都比较有效。

Table 2. The average level of distortion of the five test statistics for each sample
表2. 各样本的五种检验统计量的平均水平扭曲程度
注:平均水平扭曲程度超过0.015的加粗表示。
3.2. 小样本情况下实际检验水平的模拟与结果分析
有关时间序列分析检验方法有效性的相关研究中,很少有详细考虑到小样本条件下各检验统计量性能的情况。因此,为了判断改进方法在小样本条件下是否稳定,选取了m = 2、3、4、5(基于Battaglia (1990) [6] 、Hyndman (2014) [7] 和Hassani和Yeganegi (2020) [9] 的研究结果)以此来探究小样本情况下,m的取值是否对模拟过程造成影响。
表3展示了,小样本条件下(N = 20, 25)基于AR(1)模型的各检验统计量的模拟结果。通过计算实际检验水平随不同m值的变化率,发现五种检验方法的实际检验水平随m的变化没有明显的规律性变动。QLB统计量的实际检验水平经常出现超过名义显著性水平和QMT统计量的实际检验水平在小样本情况下全部超过名义显著性水平的情况与表2一致。
而且,可以发现当φ = 0.9时,各检验统计量的实际检验水平出现异常的情况并没有随m的变化出现改善。因此可以得出异常情况的出现与m取值无关的结论。进一步分析,发现随着样本容量的提升,模拟的实际检验水平有明显的改善,如图1所示。分析其原因为,蒙特卡罗模拟数据有随机性,当样本容量较小时,随机性的特点被放大。容易造成小样本的时间序列数据不具备平稳性,进而造成实际检验水平的模拟结果出现异常。

Table 3. Actual test levels of five test methods for small samples based on AR (1) model (α = 0.05)
表3. 基于AR(1)模型的小样本的五种检验方法的实际检验水平模拟分析结果(α = 0.05)
注:实际检验水平超过0.05的加粗表示。
4. 有限样本下的检验功效的模拟研究与结果分析
检验功效是指不犯第二类错误的概率,在备择假设的基础上重复生成大量时间序列,然后根据被研究的检验统计量的渐近分布的临界值做出接受或拒绝原假设的判断。这种情况下,拒绝原假设的比率就是该检验统计量的检验功效。
检验功效的蒙特卡罗模拟实验的具体步骤为(以AR模型为例):
1) 生成数据:以ARMA(2,2)模型
作为数据生成过程,生成时间序列数据;
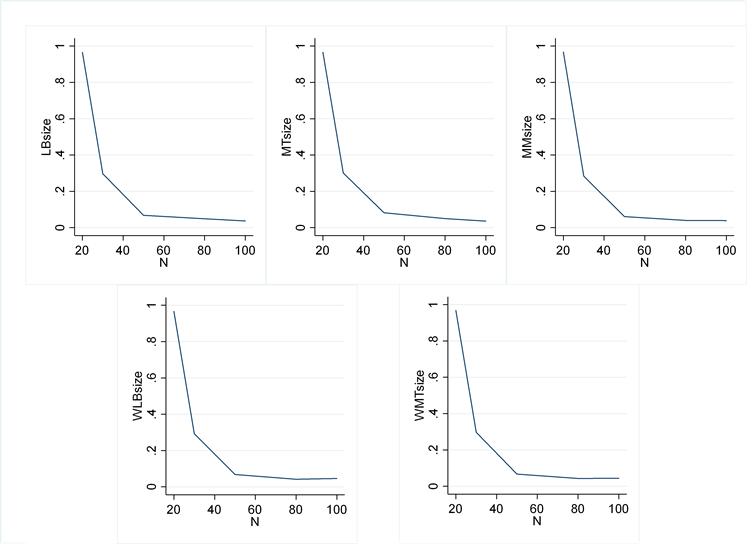
Figure 1. The actual test level of five test statistics varies with sample size (φ = 0.9)
图1. φ = 0.9时五种检验统计量的实际检验水平随样本容量变化图
2) 拟合模型:用生成的数据再次拟合AR(1)和MA(1)模型;
3) 进行检验:用五种不同的方法,在显著性水平α = 0.05的条件下,对残差序列进行自相关检验;
4) 重复实验:将步骤1~3重复1000次,计算拒绝原假设的概率。
有关检验功效模拟的模型参照了Monti (1994) [10] 中的设计,考虑了24个不同ARMA(2,2)模型作为数据生成过程。现有的相关研究中样本容量的选择多为100和500,为探究各种有限样本下各检验统计量检验功效的关系,选取N = 20、30、50、80、100五种情况,m的取值同样借鉴Battaglia (1990) [6] 中方法,显著性水平α = 0.05。
表4展示了在N = 20、30的小样本下,各检验统计量的检验功效。结果显示:QMT检验统计量的检验功效表现良好,全部大于QLB统计量的检验功效,且在多数模型中检验功效最大。QMM、QWLB和QWMT统计量在一些模型中,检验功效低于QLB统计量(如模型1、模型6~8等)。计算在各个样本容量下,QMT、QMM、QWLB和QWMT统计量与QLB统计量相比全部模型的检验功效平均变化率1分别为40.4%、−14%、−12.8%和10.4% (N = 20)以及17.5%、−8.3%、−3.3%和14.9% (N = 50)。可见在小样本下,QMT和QWMT统计量的检验效果优于QLB统计量。除此之外,在模型4、模型6~8和模型18~19中,各统计量的检验功效过小,出现小于0.05的情况。分析原因是蒙特卡罗模拟的随机性在小样本情况下被放大;ARMA模型的可逆性使特定模型生成的数程具备了AR模型或MA模型的特征。
表5展示了N = 50、80、100时,各检验统计量的检验功效。结果显示:在大样本的条件下,QMT检验统计量的优势消失,QWMT检验统计的表现更加良好。而且QMM和QWLB统计量的检验功效与小样本条件下的相比也有所改善,变得优于QLB统计量。与QLB统计量相比,QMT、QMM、QWLB和QWMT统计量的检验功效的平均变化率变为12.7%、8.6%、2.7%和15.8% (N = 50),12.6%、16.3%、10.6%和17.5% (N = 80)以及10.5%、18.4%、11.5%和21.0%。可见,在大样本下,四种检验统计量均优于QLB统计量,且QWMT检验统计最好。模型4、模型6~8和模型18~19在小样本条件下的异常情况也随着样本容量的增加有所改善。

Table 4. Simulation of test power for each test statistic based on ARMA (2,2) model I
表4. 基于ARMA(2,2)模型的各检验统计量的检验功效模拟(一)
注:每次模拟中,检验功效最大的加粗表示。

Table 5. Simulation of test power for each test statistic based on ARMA (2,2) model II
表5. 基于ARMA(2,2)模型的各检验统计的检验功效模拟(二)
注:每次模拟中,检验功效最大的加粗表示。
分析N = 20、30、50、80、100时,各检验统计量检验功效的模拟结果发现,四种改进的检验统计量的检验功效与QLB统计量对比的平均变化率随样本容量的增加呈现出一定的规律,如图2所示。QMT统计量的检验功效总是大于QLB统计量,但随样本容量的增加,此优势逐渐减弱;QMM和QWLB统计量的检验功效在小样本时小于QLB统计量,但随样本容量的增加,检验功效逐渐变大,并在N = 40左右时超过QLB统计量;QWMT统计量的检验功效一直大于QLB统计量,且随样本容量的增加而持续变大。因此,小样本时用QMT统计量做残差自相关检验更好,大样本时用QWMT统计量更优。

Figure 2. Trend chart of average change rate of four improved statistics compared to L-B statistics
图2. 四种改进统计量检验功效与L-B统计量相比的平均变化率趋势图
5. 结论
本文主要进行了L-B检验和它的四种改进方法在有限样本条件的实际检验水平与检验功效的模拟分析。
在小样本的条件下(N ≤ 30)。只有QMT和QWMT统计量的检验功效优于QLB统计量,但QMT统计量的实际检验水平表现较差,经常超过名义检验水平,且水平扭曲程度最严重。
在大样本的条件下(N > 30)。四种改进检验统计量的检验功效均优于QLB统计量,QWMT统计量的表现最好。且QMM、QWLB和QWMT统计量的实际检验水平均小于名义检验水平,其中QWLB和QWMT统计量表现更好,QMM统计量的水平扭曲程度较大。
综上所述,小样本时只有QWMT统计量检验效果较好;随着样本容量的增加,其余改进统计量的检验效果逐渐改善。相关理论研究中,小样本情形一直是被忽略的部分。实证研究中,小样本的情况却十分常见。因此,建议实证学者们警惕L-B检验在样本较小情形下的应用,可以同时使用QWMT统计量进行多次检验,确保模型设定的正确。
NOTES
1检验功效平均变化率:某个样本容量下,24个模型中,改进统计量与L-B统计量的检验功效的差值占L-B统计量检验功效的比率的平均值。