基于格子Boltzmann方法的顶盖驱动流数值模拟

Numerical Simulation of Overhead-Driven Flow Based on the Lattice Boltzmann Method

摘要: 格子Boltzmann方法是一种从介观角度来模拟流体宏观行为的方法，通过在时间和空间上使用完全离散的动力学模型来实现。利用Chapman-Enskog多尺度展开技术，我们可以将基本模型恢复到符合标准的不可压Navier-Stokes方程，给出了具体的求解过程。对于格子Boltzmann方程的边界处理，我们采用非平衡外推格式并给出了详细的推导说明。对于顶盖方腔驱动流问题，我们使用此方法进行了数值模拟，以及对模拟结果进行了分析和讨论。通过与已有的试验及数值研究结果对比，进行了鲁棒性分析，验证了使用格子Boltzmann方法模拟顶盖方腔驱动流的正确性、准确性和稳定性。

Abstract: Lattice Boltzmann method is a method to simulate the macroscopic behavior of fluid from a mesoscopic perspective, which is realized by using a completely discrete dynamic model in time and space. Using Chapman-Enskog multi-scale expansion technology, we can restore the basic mod-el to the standard incompressible Navier-Stokes equation, and give the specific solution process. For the boundary treatment of lattice Boltzmann equation, we use the non-equilibrium extrapolation scheme and give a detailed derivation. For the problem of driving flow in the square cavity of the top cover, we use this method to carry out numerical simulation, and analyze and discuss the simu-lation results. By comparing with the existing experimental and numerical results, the robustness analysis is carried out to verify the correctness, accuracy and stability of using the lattice Boltzmann method to simulate the driving flow in the square cavity of the top cover.

1. 引言

格子Boltzmann方法(lattice Boltzmann method)是最近三十年兴起的方法，目的是为了解决计算流体力学问题。它以Boltzmann方程为基础，并借助计算机技术发展而来 [1] 。

当今，计算流体力学可分为三大类：宏观方法，介观方法，微观方法 [2] 。介观层次上的格子Boltzmann方法相对于宏观和微观的计算流体力学和计算传热学方法而言，具有物理意义明确，边界条件处理简单，程序执行容易，并行性能好等性质。所以，它被看作是最具有前景的数值模拟方法中的一种 [3] 。

在车辆行业中，汽车风噪声是由车身上较小的凸起和空腔体引起的，而揭示腔内流体的运动规律和物理机制长久以来是一个重要的研究课题。顶盖方腔驱动流的研究就是基于以上述问题为工程背景的 [4] 。因此，研究这一问题既具有理论意义，也包含工程意义。顶盖方腔驱动流问题是数学物理问题上一个可以用来检验各种求解方法的有效性的经典数值模型，有许多科研工作者对其进行了数值求解。本文采用格子Boltzmann方法对其求解，并验证该方法的正确性、准确性和稳定性。

2. 模型介绍

顶盖方腔驱动流是计算流体力学中的经典问题。如图1所示，在一个每边长为1的正方形二维空腔中充满等密度的空气，其顶盖以恒定为0.1的速度向右移动，同时带动方腔内流体的流动，其他三个边界保持静止不动 [5] 。我们的目的是通过数值模拟，分析方腔中心线气体的流速，绘制气体流动的流线图，观察和研究方腔内气体的流动情况。

Figure 1. Schematic diagram of top cover drive flow

图1. 顶盖驱动流示意图

选取笛卡儿坐标系，方腔左下角为坐标原点。计算区域： $\left(x,y\right)\in \left[0,1\right]\times \left[0,1\right]$ 。初始条件如下：在方腔顶部，横坐标x方向上速度 $U=0.1$ ，纵坐标y方向上速度 $V=0$ ，在其余壁面上 $U=V=0$ ，方腔内部 $U=V=0$ ，流场初始密度 ${\rho }_0=1$ 。

流体粒子的演化过程原始方程为偏微分方程Boltzmann方程，对其进行离散，得到代数方程格子Boltzmann-BGK方程(LBGK)。设速度分布函数为f，f为空间 $r\left(x,y\right)$ 、分子速度 $\xi \left({\xi }_x,{\xi }_y\right)$ 和时间t的函数 [5] 。分布函数 $f\left(r,\xi ,t\right)$ ，是一种从介观角度考虑的函数，表示每一个粒子处于某种状态下的概率，同时 $f\left(r,\xi ,t\right)$ 也表示在t时刻，速度为 $\xi$ 的粒子密度。

网格划分：格子间距比上时间步长等于格子离散速度，则为标准LBM的控制方程 [6] 。以二维问题为例，即要求 $e_{\alpha x}={\delta }_x/{\delta }_t$ 和 $e_{\alpha y}={\delta }_y/{\delta }_t$ 。其中， $e_{\alpha x}$ 和 $e_{\alpha y}$ 分别为离散速度 $e_{\alpha }$ 在x和y方向上的分量； ${\delta }_x$ 和 ${\delta }_y$ 分别是x和y方向上的网格步长，均为常数。在此方法中，通常取 $e_{\alpha x}=e_{\alpha y}=1$ ，因而有 ${\delta }_x={\delta }_y=e_{\alpha x}{\delta }_t=e_{\alpha y}{\delta }_t=1$ ，此时的物理量都做无量纲处理，均采用的是格子单位 [7] 。

3. 数值计算方法

3.1. 从Boltzmann方程到格子Boltzmann方程

Boltzmann方程是气体动理论基本方程，与流体力学基本方程关系密切，可以通过数值模拟，来描述流体的宏观运动 [8] 。

设f为速度分布函数，先将Boltzmann方程

$\frac{\partial f}{\partial t}+\xi \cdot \frac{\partial f}{\partial r}+a\cdot \frac{\partial f}{\partial \xi }=\left(f^{\prime }{f^{\prime }}_1-f{f}_1\right)d_D^2\left|g\right|\cos \theta d\Omega d{\xi }_1=J\left(f{f}_1\right)$ (1)

右端的碰撞项线性化处理，即Boltzmann方程中的碰撞项 $J\left(f{f}_1\right)$ 替换为一个简单的算子Ω，这就是BGK近似 [9] 。得到Boltzmann-BGK方程

$\frac{\partial f}{\partial t}+\xi \cdot \frac{\partial f}{\partial r}+a\cdot \frac{\partial f}{\partial \xi }=\upsilon \left(f^{eq}-f\right)$ (2)

局部平衡态分布函数 $f^{eq}$ 随t和 $\xi \left({\xi }_x,{\xi }_y\right)$ 变化 [5] 。

再引入弛豫时间 ${\tau }_0$ ，在不考虑外力的情况下，Boltzmann-BGK方程可写作

$\frac{\partial f}{\partial t}+\xi \cdot \nabla f=\frac{1}{{\tau }_0}\left(f-f^{eq}\right)$ (3)

然后将 $\xi$ 离散为 $\left\{e_0,e_1,\cdots ,e_N\right\}$ ，N表示速度种类数。与此同时，连续的分布函数f也相对应离散为 $\left\{f_0,f_1,\cdots ,f_N\right\}$ ，其中 $f_{\alpha }=f_{\alpha }\left(r,e_{\alpha },t\right)$ ， $\alpha =0,1,\cdots ,N$ 。得到速度离散的Boltzmann-BGK方程为

$\frac{\partial f_{\alpha }}{\partial t}+e_{\alpha }\cdot \nabla f_{\alpha }=-\frac{1}{{\tau }_0}\left(f_{\alpha }-f_{\alpha }^{eq}\right)$ (4)

还需要在时间和空间上差分离散，空间采用一阶迎风格式，时间采用一阶向前格式 [10] 。

$\frac{f_{{\alpha }_i}^{n+1}-f_{{\alpha }_i}^n}{{\delta }_t}+e_{\alpha }\frac{f_{{\alpha }_{i+1}}^n-f_{{\alpha }_i}^n}{{\delta }_r}=-\frac{1}{{\tau }_0}\left(f_{\alpha }-f_{\alpha }^{eq}\right)$

$f_{{\alpha }_i}^{n+1}-f_{{\alpha }_i}^n+e_{\alpha }{\delta }_t\frac{f_{{\alpha }_{i+1}}^n-f_{{\alpha }_i}^n}{{\delta }_r}=-\frac{{\delta }_t}{{\tau }_0}\left(f_{\alpha }-f_{\alpha }^{eq}\right)$

$\left(f_{{\alpha }_i}^{n+1}+f_{{\alpha }_{i+1}}^n\right)-\left(f_{{\alpha }_i}^n+f_{{\alpha }_i}^n\right)=-\frac{1}{\tau }\left(f_{\alpha }-f_{\alpha }^{eq}\right)$

得到完全离散化的BGK方程，即为格子Boltzmann-BGK方程

$f_{\alpha }\left(r+e_{\alpha }{\delta }_t,t+{\delta }_t\right)-f_{\alpha }\left(r,t\right)=-\frac{1}{\tau }\left[f_{\alpha }\left(r,t\right)-f_{\alpha }^{eq}\left(r,t\right)\right]$ (5)

$\tau ={\tau }_0/{\delta }_t$

3.2. 格子Boltzmann方法的基本模型

通常由三个要素构成一个完整的格子Boltzmann模型，分别为：格子——离散速度模型(DVM)，平衡态分布函数以及分布函数的演化方程 [11] 。如图2所示，本文使用D2Q9 (2维9速)模型 [12] 。其分布函数的演化方程为：

$f_{\alpha }\left(r+e_{\alpha }{\delta }_t,t+{\delta }_t\right)-f_{\alpha }\left(r,t\right)=-\frac{1}{\tau }\left[f_{\alpha }\left(r,t\right)-f_{\alpha }^{eq}\left(r,t\right)\right]$ (6)

式中， $f_{\alpha }$ 为粒子沿 $\alpha$ 方向速度分布函数；r为粒子空间位置； ${\delta }_t$ 为时间步长； $\tau$ 为无量纲松弛时间； $e_{\alpha }$ 表示速度配置：

$e_{\alpha }=\{\begin{array}{l}\left(0,0\right),\alpha =0\\ \left[\cos \left(\frac{\pi }{2}\left(\alpha -1\right)\right),\sin \left(\frac{\pi }{2}\left(\alpha -1\right)\right)\right]c,\alpha =1~4\\ \sqrt{2}\left[\cos \left(\frac{\pi }{2}\left(\alpha -1\right)+\frac{\pi }{2}\right),\sin \left(\frac{\pi }{2}\left(\alpha -1\right)+\frac{\pi }{2}\right)\right]c,\alpha =5~8\end{array}$ (7)

式中， $c=\frac{{\delta }_x}{{\delta }_y}$ 分别为网格步长和时间步长，且通常有 ${\delta }_x={\delta }_y$ 。

$e_{\alpha }$ 表示了粒子的运动方向，可表示为

$e_0=\left(0,0\right),e_{1,3}=\left(\pm c,0\right),e_{2,4}=\left(0,\pm c\right),e_{5,6}=\left(\pm c,c\right),e_{7,8}=\left(\mp c,-c\right)$

Figure 2. D2Q9 model

图2. D2Q9模型

$f_{\alpha }^{eq}\left(r,t\right)$ 为平衡态分布函数，可表示为

$f_{\alpha }^{eq}=\rho {\omega }_{\alpha }\left[1+\frac{e_{\alpha }\cdot u}{c_s^2}+\frac{{\left(e_{\alpha }\cdot u\right)}^2}{2c_s^4}-\frac{u^2}{2c_s^2}\right]$ (8)

式中，c_s为格子声速， ${\omega }_{\alpha }$ 为权系数， $u=\left(u_{\text{1}},u_{\text{2}}\right)$ 为气体宏观速度 [5] 。

$f_{\alpha }^{eq}=\frac{4}{9}\rho \left(1-\frac{3}{2}\frac{u^2}{c^2}\right),\alpha =0$

$f_{\alpha }^{eq}=\frac{1}{9}\rho \left[1+3\frac{e_{\alpha }\cdot u}{c^2}+\frac{9}{2}\frac{{\left(e_{\alpha }\cdot u\right)}^2}{c^4}-\frac{3}{2}\frac{u^2}{c^2}\right],\alpha =1,2,3,4$ (9)

$f_{\alpha }^{eq}=\frac{1}{36}\rho \left[1+3\frac{e_{\alpha }\cdot u}{c^2}+\frac{9}{2}\frac{{\left(e_{\alpha }\cdot u\right)}^2}{c^4}-\frac{3}{2}\frac{u^2}{c^2}\right],\alpha =5,6,7,8$

由分布函数，可求得模型的宏观密度和速度：

$\rho ={\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }},u=\frac{1}{\rho }{\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }{e}_{\alpha }}$ (10)

应用Chapman-Enskog多尺度展开技术我们能从式(6)中恢复推导出其基本模型对应的宏观方程，即能得到不可压缩的Navier-Stokes方程。以下是对此过程的详细求解过程。

在多尺度技术中，通常使用以下三种形式的时间尺度： $t^{*}$ (离散时间)、 $t_1=k{t}^{*}$ (连续时间)、 $t_2=k^2{t}^{*}$ (连续时间)，两种空间尺度： $r^{*}$ (离散空间)、 $r_1=k{r}^{*}$ (连续空间) [5] 。从而时间导数和空间导数有：

$\frac{\partial }{\partial t}=\frac{\partial }{\partial t_1}\cdot \frac{\partial t_1}{\partial t}+\frac{\partial }{\partial t_2}\cdot \frac{\partial t_2}{\partial t}=k\frac{\partial }{\partial t_1}+k^2\frac{\partial }{\partial t_2}$ (11)

$\frac{\partial }{\partial r}=\frac{\partial }{\partial r_1}\cdot \frac{\partial r_1}{\partial r}=k\frac{\partial }{\partial r_1}$ (12)

Chapman-Enskog展开还需要对分布函数进行展开，即假设分布函数 $f_{\alpha }\left(r,t\right)$ 已经离平衡态不远，并趋于平衡态。因此 $f_{\alpha }\left(r,t\right)$ 可以展开为k幂级数形式：

$f_{\alpha }=f_{\alpha }^{eq}+k{f}_{\alpha }^{\left(1\right)}+k^2{f}_{\alpha }^{\left(2\right)}+\cdots$ (13)

不考虑外力的格子Boltzmann方程如下：

$f_{\alpha }\left(r+e_{\alpha }{\delta }_t,t+{\delta }_t\right)-f_{\alpha }\left(r,t\right)=-\frac{1}{\tau }\left[f_{\alpha }\left(r,t\right)-f_{\alpha }^{eq}\left(r,t\right)\right]$ (14)

对式(14)的左端对时间与空间做泰勒展开可得：

$\begin{array}{l}{f}_{\alpha }\left(r+e_{\alpha }{\delta }_t,t+{\delta }_t\right)-f_{\alpha }\left(r,t\right)\\ =\left(\frac{\partial }{\partial r}\cdot e_{\alpha }{\delta }_t+\frac{\partial }{\partial t}{\delta }_t\right)f_{\alpha }\left(r,t\right)+\frac{1}{2!}{\left(\frac{\partial }{\partial r}\cdot e_{\alpha }{\delta }_t+\frac{\partial }{\partial t}{\delta }_t\right)}^2{f}_{\alpha }\left(r,t\right)\\ ={\delta }_t\left(\frac{\partial }{\partial t}+e_{\alpha }\cdot \nabla \right)f_{\alpha }\left(r,t\right)+\frac{1}{2!}{\delta }_t^2{\left(\frac{\partial }{\partial t}+e_{\alpha }\cdot \nabla \right)}^2{f}_{\alpha }\left(r,t\right)\\ =-\frac{1}{\tau }\left[f_{\alpha }\left(r,t\right)-f_{\alpha }^{eq}\left(r,t\right)\right]+O\left({\delta }_t^3\right)\end{array}$ (15)

${\delta }_t\left(\frac{\partial }{\partial t}+e_{\alpha }\cdot \nabla \right)f_{\alpha }+\frac{{\delta }_t^2}{2}{\left(\frac{\partial }{\partial t}+e_{\alpha }\cdot \nabla \right)}^2+\frac{1}{\tau }\left(f_{\alpha }-f_{\alpha }^{eq}\right)+O\left({\delta }_t^3\right)=0$ (16)

把式(11)、(12)、(13)带到式(16)可以得到：

$\begin{array}{l}{\delta }_t\left(k\frac{\partial }{\partial t_1}+k^2\frac{\partial }{\partial t_2}+k{e}_{\alpha }\cdot {\nabla }_1\right)\left(f_{\alpha }^{eq}+k{f}_{\alpha }^{\left(1\right)}+k^2{f}_{\alpha }^{\left(2\right)}+\cdots \right)\\ +\frac{{\delta }_t^2}{2}{\left(k\frac{\partial }{\partial t_1}+k^2\frac{\partial }{\partial t_2}+k{e}_{\alpha }\cdot {\nabla }_1\right)}^2\left(f_{\alpha }^{eq}+k{f}_{\alpha }^{\left(1\right)}+k^2{f}_{\alpha }^{\left(2\right)}+\cdots \right)\\ +\frac{1}{\tau }\left(k{f}_{\alpha }^{\left(1\right)}+k^2{f}_{\alpha }^{\left(2\right)}+\cdots \right)+O\left({\delta }_t^3\right)=0\end{array}$ (17)

比较一下 $k^1$ 和 $k^2$ 的系数，我们可以得到

$k^1:k{\delta }_t\frac{\partial }{\partial t_1}{f}_{\alpha }^{eq}+k{\delta }_t{e}_{\alpha }\cdot {\nabla }_1{f}_{\alpha }^{eq}+\frac{1}{\tau }k{f}_{\alpha }^{\left(1\right)}=0$ (18)

$\left(\frac{\partial }{\partial t_1}+e_{\alpha }\cdot {\nabla }_1\right)f_{\alpha }^{eq}+\frac{1}{\tau {\delta }_t}{f}_{\alpha }^{\left(1\right)}=0$ (19)

$k^2:{\delta }_t{k}^2\frac{\partial }{\partial t_2}{f}_{\alpha }^{eq}+\frac{{\delta }_t^2}{2}{\left(k\frac{\partial }{\partial t_1}+k{e}_{\alpha }\cdot {\nabla }_1\right)}^2{f}_{\alpha }^{eq}+\frac{k^2}{\tau }{f}_{\alpha }^{\left(2\right)}+{\delta }_t{k}^2\left(\frac{\partial }{\partial t_1}+e_{\alpha }\cdot {\nabla }_1\right)f_{\alpha }^{\left(1\right)}=0$ (20)

$\frac{\partial f_{\alpha }^{eq}}{\partial t_2}+\left(\frac{\partial }{\partial t_1}+e_{\alpha }\cdot {\nabla }_1\right)f_{\alpha }^{\left(1\right)}+\frac{{\delta }_t}{2}{\left(\frac{\partial }{\partial t_1}+e_{\alpha }\cdot {\nabla }_1\right)}^2{f}_{\alpha }^{eq}+\frac{1}{\tau {\delta }_t}{f}_{\alpha }^{\left(2\right)}=0$ (21)

由式(19)，可以将式(21)简化为

$k^2:\frac{\partial f_{\alpha }^{eq}}{\partial t_2}+\left(\frac{\partial }{\partial t_1}+e_{\alpha }\cdot {\nabla }_1\right)\left(1-\frac{1}{2\tau }\right)f_{\alpha }^{\left(1\right)}+\frac{1}{\tau {\delta }_t}{f}_{\alpha }^{\left(2\right)}=0$ (22)

平衡态分布函数需满足矩方程：

${\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{eq}}=\rho$ ， ${\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{eq}{e}_{\alpha }=\rho }u$

再根据式(10)密度、速度的定义，我们可以得到：

${\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{eq}}=\rho ={\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }}={\displaystyle \underset{\alpha }{\sum }\left(f_{\alpha }^{eq}+k{f}_{\alpha }^{\left(1\right)}+k^2{f}_{\alpha }^{\left(2\right)}+\cdots \right)}={\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{eq}}+{\displaystyle \underset{\alpha }{\sum }\left(k{f}_{\alpha }^{\left(1\right)}+k^2{f}_{\alpha }^{\left(2\right)}+\cdots \right)}$ (23)

因此我们能得到第一个关系式

${\displaystyle \underset{\alpha }{\sum }k{f}_{\alpha }^{\left(1\right)}}={\displaystyle \underset{\alpha }{\sum }{k}^2{f}_{\alpha }^{\left(2\right)}}=\cdots =0\Rightarrow {\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{\left(n\right)}}=0$ (24)

同样，我们可以得到

$\begin{array}{c}\frac{1}{\rho }{\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{eq}{e}_{\alpha }}=u=\frac{1}{\rho }{\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }{e}_{\alpha }}=\frac{1}{\rho }{\displaystyle \underset{\alpha }{\sum }\left(f_{\alpha }^{eq}+k{f}_{\alpha }^{\left(1\right)}+k^2{f}_{\alpha }^{\left(2\right)}+\cdots \right)e_{\alpha }}\\ =\frac{1}{\rho }{\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{eq}}{e}_{\alpha }+\frac{1}{\rho }{\displaystyle \underset{\alpha }{\sum }\left(k{f}_{\alpha }^{\left(1\right)}{e}_{\alpha }+k^2{f}_{\alpha }^{\left(2\right)}{e}_{\alpha }+\cdots \right)}\end{array}$ (25)

所以我们得到第二个关系式

${\displaystyle \underset{\alpha }{\sum }k{f}_{\alpha }^{\left(1\right)}{e}_{\alpha }}={\displaystyle \underset{\alpha }{\sum }{k}^2{f}_{\alpha }^{\left(2\right)}{e}_{\alpha }}=\cdots =0\Rightarrow {\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{\left(n\right)}{e}_{\alpha }}=0$ (26)

对式(19)求速度的零阶矩和一阶矩

${\displaystyle \underset{\alpha }{\sum }\left(\frac{\partial }{\partial t_1}+e_{\alpha }\cdot {\nabla }_1\right)f_{\alpha }^{eq}}+{\displaystyle \underset{\alpha }{\sum }\frac{1}{\tau {\delta }_t}{f}_{\alpha }^{\left(1\right)}}=0$ (27)

${\displaystyle \underset{\alpha }{\sum }\frac{\partial }{\partial t_1}{f}_{\alpha }^{eq}}=\frac{\partial \rho }{\partial t_1}$ (28)

${\displaystyle \underset{\alpha }{\sum }{e}_{\alpha }\cdot {\nabla }_1{f}_{\alpha }^{eq}}={\nabla }_1\cdot {\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{eq}{e}_{\alpha }}={\nabla }_1\cdot \left(\rho u\right)$ (29)

${\displaystyle \underset{\alpha }{\sum }\frac{1}{\tau {\delta }_t}{f}_{\alpha }^{\left(1\right)}}=\frac{1}{\tau {\delta }_t}{\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{\left(1\right)}}=0$ (30)

${\displaystyle \underset{\alpha }{\sum }\left(\frac{\partial }{\partial t_1}+e_{\alpha }\cdot {\nabla }_1\right)f_{\alpha }^{eq}{e}_{\alpha }}+{\displaystyle \underset{\alpha }{\sum }\frac{1}{\tau {\delta }_t}{f}_{\alpha }^{\left(1\right)}{e}_{\alpha }}=0$ (31)

${\displaystyle \underset{\alpha }{\sum }\left(\frac{\partial }{\partial t_1}+e_{\alpha i}\cdot {\nabla }_{1i}\right)f_{\alpha }^{eq}{e}_{\alpha j}}+{\displaystyle \underset{\alpha }{\sum }\frac{1}{\tau {\delta }_t}{f}_{\alpha }^{\left(1\right)}{e}_{\alpha }}=0$ (32)

${\displaystyle \underset{\alpha }{\sum }\frac{\partial }{\partial t_1}{f}_{\alpha }^{eq}{e}_{\alpha j}}=\frac{\partial }{\partial t_1}{\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{eq}{e}_{\alpha j}}=\frac{\partial }{\partial t_1}\left(\rho u_j\right)$ (33)

$\begin{array}{c}{\displaystyle \underset{\alpha }{\sum }{e}_{\alpha i}\cdot {\nabla }_{1i}{f}_{\alpha }^{eq}{e}_{\alpha j}}={\displaystyle \underset{\alpha }{\sum }{e}_{\alpha i}\cdot \frac{\partial }{\partial r_{1i}}{f}_{\alpha }^{eq}{e}_{\alpha j}}=\frac{\partial }{\partial r_{1i}}{\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{eq}{e}_{\alpha i}{e}_{\alpha j}}\\ =\frac{\partial }{\partial r_{1i}}{\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{eq}{e}_{\alpha i}{e}_{\alpha j}}=\frac{\partial }{\partial r_{1i}}\left(\rho u_i{u}_j+p{\delta }_{ij}\right)\end{array}$ (34)

${\displaystyle \underset{\alpha }{\sum }\frac{1}{\tau {\delta }_t}{f}_{\alpha }^{\left(1\right)}{e}_{\alpha }}=\frac{1}{\tau {\delta }_t}{\displaystyle \underset{\alpha }{\sum }{f}_{\alpha }^{\left(1\right)}{e}_{\alpha }}=0$ (35)

故，得到t₁时间尺度上的宏观方程

$\frac{\partial \rho }{\partial t_1}+{\nabla }_1\left(\rho u\right)=0$ (36)

$\frac{\partial }{\partial t_1}\left(\rho u_j\right)+\frac{\partial }{\partial r_{1i}}\left(\rho u_i{u}_j\right)=-\frac{\partial p}{\partial r_{1j}}$ (37)

同理可得t₂时间尺度上的宏观方程

$\frac{\partial \rho }{\partial t_2}=0$ (38)

$\frac{\partial }{\partial t_2}\left(\rho u_j\right)+\left(1-\frac{1}{2\tau }\right)\frac{\partial }{\partial r_{1i}}\left({\displaystyle \underset{\alpha }{\sum }{e}_{\alpha i}{e}_{\alpha j}{f}_{\alpha }^{\left(1\right)}}\right)=0$ (39)

$\begin{array}{c}{\displaystyle \underset{\alpha }{\sum }{e}_{\alpha i}{e}_{\alpha j}}{f}_{\alpha }^{\left(1\right)}=-\tau {\delta }_t{\displaystyle \underset{\alpha }{\sum }{e}_{\alpha i}{e}_{\alpha j}\left(\frac{\partial }{\partial t_1}+e_{\alpha }\cdot {\nabla }_1\right)f_{\alpha }^{eq}}\\ =-\tau {\delta }_t{\displaystyle \underset{\alpha }{\sum }\left(e_{\alpha i}{e}_{\alpha j}\frac{\partial }{\partial t_1}{f}_{\alpha }^{eq}+e_{\alpha i}{e}_{\alpha j}{e}_{\alpha l}\cdot {\nabla }_{1l}{f}_{\alpha }^{eq}\right)}\\ =-\tau {\delta }_t\left[\frac{\partial }{\partial t_1}\left(\rho u_i{u}_j+\rho c_s^2{\delta }_{ij}\right)+\frac{\partial }{\partial r_{1l}}\left({\displaystyle \underset{\alpha }{\sum }{e}_{\alpha i}{e}_{\alpha j}{e}_{\alpha }{}_l{f}_{\alpha }^{eq}}\right)\right]\end{array}$ (40)

由式(36)可得

$\frac{\partial }{\partial t_1}\left(\rho c_s^2{\delta }_{ij}\right)=c_s^2\frac{\partial \rho }{\partial t_1}{\delta }_{ij}=-c_s^2{\nabla }_1\cdot \left(\rho u\right){\delta }_{ij}$ (41)

由式(36)和(37)可得

$\begin{array}{c}\frac{\partial }{\partial t_1}\left(\rho u_i{u}_j\right)=u_j\frac{\partial }{\partial t_1}\left(\rho u_i\right)+u_i\frac{\partial }{\partial t_1}\left(\rho u_j\right)-u_i{u}_j\frac{\partial \rho }{\partial t_1}\\ =u_j\left[-\frac{\partial }{\partial r_{1l}}\left(\rho u_i{u}_l\right)-\frac{\partial }{\partial r_{1i}}\left(\rho c_s^2{\delta }_{il}\right)\right]+u_i\left[-\frac{\partial }{\partial r_{1l}}\left(\rho u_j{u}_l\right)-\frac{\partial }{\partial r_{1j}}\left(\rho c_s^2{\delta }_{jl}\right)\right]-u_i{u}_j\frac{\partial \left(\rho u_l\right)}{\partial r_{1l}}\\ =-u_j\frac{\partial }{\partial r_{1l}}\left(\rho u_i{u}_l\right)-u_j{c}_s^2\frac{\partial \rho }{\partial r_{1i}}-u_i\frac{\partial }{\partial r_{1l}}\left(\rho u_j{u}_l\right)-u_i{c}_s^2\frac{\partial \rho }{\partial r_{1j}}+u_i{u}_j\frac{\partial \left(\rho u_l\right)}{\partial r_{1l}}\\ =-u_j{c}_s^2\frac{\partial \rho }{\partial r_{1i}}-u_i{c}_s^2\frac{\partial \rho }{\partial r_{1j}}-\rho u_j{u}_l\frac{\partial u_i}{\partial r_{1l}}-u_i\frac{\partial }{\partial r_{1l}}\left(\rho u_j{u}_l\right)\\ =-u_j{c}_s^2\frac{\partial \rho }{\partial r_{1i}}-u_i{c}_s^2\frac{\partial \rho }{\partial r_{1j}}-\frac{\partial }{\partial r_{1l}}\left(\rho u_i{u}_j{u}_l\right)\end{array}$ (42)

根据D2Q9的平衡态分布函数

$\begin{array}{c}\frac{\partial }{\partial r_{1l}}\left({\displaystyle \underset{\alpha }{\sum }{e}_{\alpha i}{e}_{\alpha j}{e}_{\alpha }{}_l{f}_{\alpha }^{eq}}\right)=\frac{\partial }{\partial r_{1l}}\left({\displaystyle \underset{\alpha }{\sum }{e}_{\alpha i}{e}_{\alpha j}{e}_{\alpha }{}_l\rho {\omega }_{\alpha }\left(1+\frac{e_{\alpha }\cdot u}{c_s^2}+\frac{{\left(e_{\alpha }\cdot u\right)}^2}{2c_s^4}-\frac{u^2}{2c_s^2}\right)}\right)\\ =\frac{\partial }{\partial r_{1l}}({\displaystyle \underset{\alpha =1}{\overset{4}{\sum }}{e}_{\alpha i}{e}_{\alpha j}{e}_{\alpha }{}_l\rho {\omega }_{\alpha }\left(1+\frac{e_{\alpha }\cdot u}{c_s^2}+\frac{{\left(e_{\alpha }\cdot u\right)}^2}{2c_s^4}-\frac{u^2}{2c_s^2}\right)}\\ +{\displaystyle \underset{\alpha =5}{\overset{8}{\sum }}{e}_{\alpha i}{e}_{\alpha j}{e}_{\alpha }{}_l\rho {\omega }_{\alpha }\left(1+\frac{e_{\alpha }\cdot u}{c_s^2}+\frac{{\left(e_{\alpha }\cdot u\right)}^2}{2c_s^4}-\frac{u^2}{2c_s^2}\right)})\\ =\frac{\partial }{\partial r_{1l}}\left({\displaystyle \underset{\alpha =1}{\overset{4}{\sum }}{e}_{\alpha i}{e}_{\alpha j}{e}_{\alpha }{}_l\rho \frac{1}{9}\frac{e_{\alpha }\cdot u}{c_s^2}+{\displaystyle \underset{\alpha =5}{\overset{8}{\sum }}{e}_{\alpha i}{e}_{\alpha j}{e}_{\alpha }{}_l\rho \frac{1}{36}\frac{e_{\alpha }\cdot u}{c_s^2}}}\right)\\ =\frac{\partial }{\partial r_{1l}}\left(\frac{2\rho u_m}{9c_s^2}{c}^4{\delta }_{ijlm}+\frac{\rho u_m}{36c_s^2}\left(4c^2{\Delta }_{ijlm}-8c^2{\delta }_{ijlm}\right)\right)\end{array}$ (43)

$\begin{array}{l}=\frac{\partial }{\partial r_{1l}}\left(\frac{2}{3}\rho u_m{c}^2{\delta }_{ijlm}+\frac{1}{3}\rho u_m{c}^2{\Delta }_{ijlm}-\frac{2}{3}\rho u_m{c}^2{\delta }_{ijlm}\right)\\ =\frac{\partial }{\partial r_{1l}}\left(\frac{1}{3}\rho u_m{c}^2\left({\delta }_{ij}{\delta }_{lm}+{\delta }_{il}{\delta }_{jm}+{\delta }_{im}{\delta }_{jl}\right)\right)\\ =\frac{\partial }{\partial r_{1l}}\left(\rho c_s^2\left({\delta }_{ij}{u}_l+{\delta }_{il}{u}_j+{\delta }_{jl}{u}_i\right)\right)\\ =c_s^2{\nabla }_1\cdot \left(\rho u\right){\delta }_{ij}+u_j{c}_s^2\frac{\partial \rho }{\partial r_{1i}}+u_i{c}_s^2\frac{\partial \rho }{\partial r_{1j}}+\rho c_s^2\left(\frac{\partial u_j}{\partial r_{1i}}+\frac{\partial u_i}{\partial r_{1j}}\right)\end{array}$

其中 $\frac{c^2}{c_s^2}=3$ 。

将式(41)、(42)和(43)代入式(40)得

${\displaystyle \underset{\alpha }{\sum }{e}_{\alpha i}{e}_{\alpha j}}{f}_{\alpha }^{\left(1\right)}=-\tau {\delta }_t\left[\rho c_s^2\left(\frac{\partial u_j}{\partial r_{1i}}+\frac{\partial u_i}{\partial r_{1j}}\right)-\frac{\partial }{\partial r_{1l}}\left(\rho u_i{u}_j{u}_l\right)\right]$ (44)

联立t₁和t₂时间尺度方程可得模型对应的宏观方程

$\frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho u\right)=0$ (45)

$\frac{\partial \left(\rho u\right)}{\partial t}+\nabla \cdot \left(\rho uu\right)=-\nabla p+\nabla \cdot \left(\rho \upsilon \left(\nabla u+{\left(\nabla u\right)}^{{\rm T}}\right)-\frac{\upsilon }{\rho }\nabla \cdot \left(\rho uuu\right)\right)$ (46)

其中 $\upsilon =c_s^2\left(\tau -\frac{1}{2}\right){\delta }_t=\frac{1}{3}{c}^2\left(\tau -\frac{1}{2}\right){\delta }_t$ ， $\upsilon$ 为运动粘度系数。

与标准的可压缩N-S方程相比，式(46)存在动量偏差 [13] 。对低马赫数流动来说 $\nabla \cdot \left(\rho uuu\right)$ 可以忽略，如果流体密度为常数 $\rho ={\rho }_0$ ，此时宏观方程为

$\nabla \cdot u=0$ (47)

$\frac{\partial u}{\partial t}+\nabla \cdot \left(uu\right)=-\frac{1}{{\rho }_0}\nabla p+\upsilon \nabla \cdot \left(\nabla u+{\left(\nabla u\right)}^{{\rm T}}\right)$ (48)

式中， $\nabla \cdot {\left(\nabla u\right)}^{{\rm T}}=\nabla \left(\nabla \cdot u\right)=0$ ，于是上述方程为标准的不可压N-S方程组。

3.3. 格子Boltzmann方法的边界处理

本文采用Guo等人提出的非平衡外推格式，即将边界节点上的分布函数分解成平衡态和非平衡态来讨论 [14] 。

Figure 3. Unbalanced extrapolation format

图3. 非平衡外推格式

如图3所示，在D2Q9模型中，假设边界上的是TOP，流场中的是SRQ。在t时刻，因为边界格点O处没有f₂、f₅和f₆方向迁移来的粒子，因此分布函数f₂、f₅和f₆都是未知的，但格点Q、R、S的分布函数、宏观密度和速度均已知。分布函数在O点的值是未知的，为了确定在此处的值，将此处的值分解为平衡态和非平衡态，即

$f_{\alpha }\left(O,t\right)=f_{\alpha }^{eq}\left(O,t\right)+f_{\alpha }^{neq}\left(O,t\right)$

其中 $f_{\alpha }^{neq}\left(O,t\right)$ 是非平衡态部分。

对于平衡态部分，对速度边界条件，O点速度 $u\left(O,t\right)$ 已知，密度 $\rho \left(O,t\right)$ 未知的情况下，可用临近的R点密度 $\rho \left(R,t\right)$ 来代替。O点的平衡态分布函数由 $f_{\alpha }^{eq}\left(O,t\right)=Feq\left(\rho \left(R,t\right),u\left(O,t\right)\right)$ 近似获得。对于非平衡态部分，则可以使用临近格点R处的非平衡态函数来近似，即

$f_{\alpha }^{neq}\left(O,t\right)=f_{\alpha }^{neq}\left(R,t\right)=f_{\alpha }\left(R,t\right)-f_{\alpha }^{eq}\left(R,t\right)=f_{\alpha }\left(R,t\right)-Feq\left(\rho \left(R,t\right),u\left(R,t\right)\right)$

因此，可得到O点的近似分布函数：

$f_{\alpha }\left(O,t\right)=f_{\alpha }^{eq}\left(O,t\right)+\left[f_{\alpha }\left(R,t\right)-f_{\alpha }^{eq}\left(R,t\right)\right]$ (49)

3.4. 小结

格子Boltzmann方法的计算过程是一个循环演化的过程，每前进一个时步，完成一次循环。

1、全场初始化，确定各节点上的宏观密度 $\rho$ 和宏观速度u以及分布函数 $f_{\alpha }$ ；

2、接着可以得到此时的平衡态分布函数 $f_{\alpha }^{eq}$ ；

3、再根据LBGK碰撞模型可以得到碰撞后的密度分布函数 $f_{\alpha }^{+}$ ；

4、再通过迁移，就可以得到下一时刻的密度分布函数 $f_{\alpha }\left(r+e_{\alpha }{\delta }_t,t+{\delta }_t\right)$ ；

5、由某一时刻的密度分布函数，可以计算出该时刻的宏观密度和宏观速度；

6、边界处理；

7、判断收敛性。重复上述2~6过程，可以实现整个过程的不断演化。

以上是对LBM的分析。

4. 数值模拟

4.1. 模拟过程

取边长为1的正方形腔体，选择笛卡儿坐标系，方腔左下角为坐标原点，格子取为256 × 256 [4]。

初始条件：方腔顶部， $U=0.1,V=0$ ；其余壁面， $U=V=0$ ；方腔内部， $U=V=0$ ；初始密度 ${\rho }_0=1$ ，由式(8)计算平衡态分布函数 $f_{\alpha }^{eq}$ ，在 $t=0$ 时刻， $f_{\alpha }=f_{\alpha }^{eq}$ 。

根据式(5)进行迭代计算，边界处理采用非平衡外推格式。在数值模拟中，运动黏度系数可可由雷诺数定义式反算获得： $\upsilon =U{L}_N/Re$ ，其中，U为顶盖驱动速度， $L_N$ 为方腔顶部的格子数，即 $L_N=256$ 。

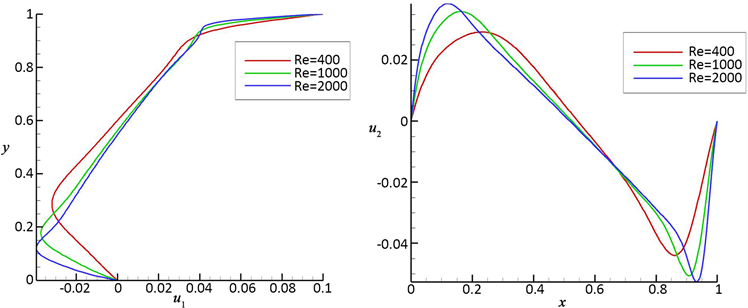
Figure 4. Center line velocity u₁, u₂ of square cavity

图4. 方腔中心线速度u₁，u₂

各参数均为格子单位，终止条件设为相邻两个时间步的最大流函数差值小于10⁻⁶ [4] 。

4.2. 模拟结果

图4表示出了雷诺数分别为400、1000、2000时，通过方腔中心x = 0.5，水平方向的速度分量u₁随纵坐标y的变化，与通过方腔中心y = 0.5，垂直方向的速度分量u₂随横坐标x的变化。可以观察到，随着雷诺数的增大，速度曲线的波峰变化越大。说明雷诺数越大(流体的惯性力越大和粘性力越小)，速度变化越大。

图5分别示出了雷诺数为400和1000时，中心线速度结果和Ghia的结果对比。通过对比发现，方腔的中心线速度分量u₁，u₂和Ghia的结果基本保持一致。表明了我们结果的正确性和准确性。

在图6中，对于不同的雷诺数，我们对水平初速度U作了一个微小的扰动，观察图形的变化，发现图形的形态几乎没有改变，即该系统在稳定状态下受到较小的扰动后仍能回到一个相近的稳定状态，表明了这个算法和模型具有鲁棒性。

在图7中，对于不同的雷诺数，我们画出了流线图。显然，可以看到在方腔内部生成了大小不同的旋涡。三个图的中心都出现一个一级涡，在左右下角都会出现一个二级涡。当Re = 2000时，左上角出现了第三个二级涡。当Re = 400时，一级涡中心在方腔中心偏右上。当雷诺数变大，左、右下角的涡也随

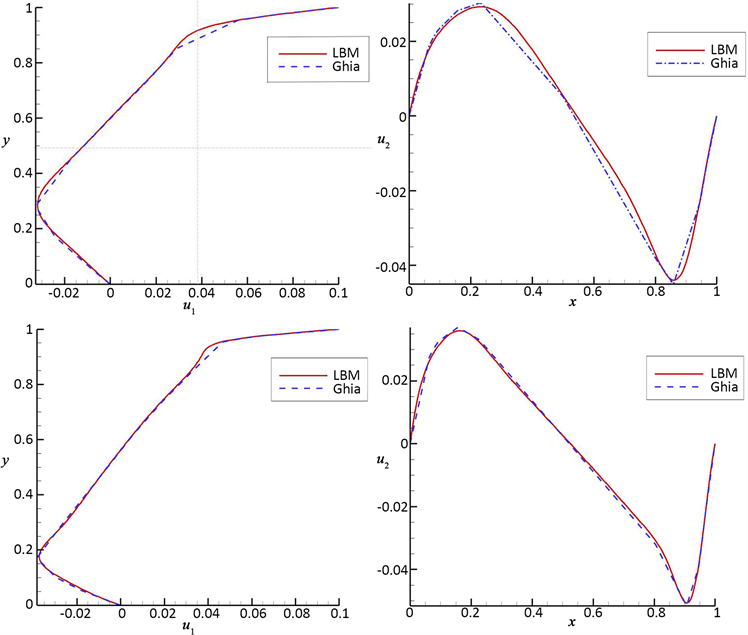
Figure 5. Comparison of centerline velocity results with Ghia

图5. 中心线速度结果与Ghia的对比

Figure 6. Comparison of centerline velocities at different Reynolds numbers and horizontal initial velocities

图6. 不同雷诺数和水平初速度下中心线速度对比

Figure 7. Streamline diagram of top cover drive flow with Re = 400, 1000, 2000

图7. Re = 400、1000、2000顶盖驱动流的流线图

之增大，且一级涡中心向方腔中心移动 [15] 。因此，可以清晰地看出雷诺数对流动模式的影响。

5. 结束语

本文详细讨论了LBM，并以LBM为基础，对顶盖方腔驱动流中的流场进行了数值模拟，采用的是D2Q9模型，在边界条件上采用非平衡外推格式，计算简单，易于实现。得到并详细讨论了雷诺数分别为Re = 400，1000，2000时的数值结果。与前人已有的数值研究结果进行对比，表明了该方法的正确性、准确性和鲁棒性。LBM对理解流体流动有现实意义，拥有广阔的研究前景。