超导拓扑表面态的自洽平均场理论

Self-Consistent Mean-Field Theory of Superconducting Topological Surface States

摘要: 我们采用自洽平均场的方法，来求解FeSeTe薄膜界面处的拓扑超导表面态的能隙。用平均场近似得到近似的哈密顿量，对该哈密顿量进行粒子–准粒子变换(Bogoliubov-Valatin)简化为无相互作用的准粒子体系，得到能隙的费米算子表达式。分别在零温及有限温度下展开该表达式，利用费米算子的对易关系及准粒子体系满足的分布特性，得到两种温度状态下的能隙自洽式。通过超导转变的特殊性算出超导转变温度后，在此基础上自洽地数值解出零温到超导转变温度范围内能隙随温度的变化关系。对拓扑表面态超导能隙的研究，可以从中得到超导态的热力学性质的变化。同时对寻找适用于拓扑量子计算的马约拉纳零能摸具有参考意义。

Abstract: We use the self-consistent mean-field method to solve the energy gap of the topological super-conducting surface state at the interface of the FeSeTe film. The approximate Hamiltonian is obtained by the mean field approximation. The Bogoliubov quasi-particle transformation of the Hamiltonian is simplified to a non-interacting quasi-particle system, and the Fermi operator expression of the energy gap is obtained. The expression is expanded at zero temperature and finite temperature respectively. By using the commutation relationship of Fermi operator and the distribution characteristics of quasi-particle system, the energy gap self-consistent formulas under two temperature states are obtained. After the superconducting transition temperature is calculated by the particularity of the superconducting transition, the relationship between the energy gap and temperature in the range of zero temperature to superconducting transition temperature is solved numerically. The study of the superconducting energy gap of the topological surface state can obtain the change of the thermodynamic properties of the superconducting state. At the same time, it has reference significance for finding Majorana zero modes suitable for topological quantum computing.

1. 引言

拓扑超导的第一个实例可追溯到1980年，von Klitzingd等人发现在量子霍尔(QH)状态下，二维(2D)样品的大部分是绝缘的 [1] ，并且电流仅沿样品边缘携带。这种单向电流的流动避免了耗散并产生量子化的霍尔效应。该现象也被称作整数量子霍尔效应，这种现象无法简单地用朗道–金兹堡理论(Landau and Lifshitz, 1980)来解释。引起量子霍尔效应的态并没有打破任何对称性，却明显是一种新的物相，这引发一种新的物相分类范式，即拓扑序，通过拓扑序的不同来区分不同的拓扑绝缘体 [2] [3] 。拓扑绝缘体在表面表现出的奇特特性使其可以作为很好地寻找用于量子计算的马约拉纳费米子的平台 [4] [5] [6] 。马约拉纳粒子的概念最早在1937年由意大利科学家Mjorana提出，它的反粒子为本身。凝聚态中的马约拉纳费米子也被称作马约拉纳零能摸，作为一种特殊的零能激发态出现在凝聚态系统中，具有非阿贝尔统计性质，能应用于可容错拓扑量子计算 [7] 。Fu-Kane预测拓扑超导体表面态会受马约拉纳费米子激发产生超导能隙 [8] ，FeSe体系是结构最简单的铁基超导体，可用于构建超导拓扑表面态 [9] [10] 。2008年，M. K. Wu等人发现了超导转变温度为8 K的铁基超导体，值得注意的是，施加4.5 GPa压力后，超导转变温度可达37 K [11] 。之后的扫描隧道显微镜(STM)测量及角分辨电子光谱(ARPES)研究得到费米能与超导能隙十分接近，在空穴能带费米能级为4 ± 2.5 meV左右，电子能带费米能级为10 ± 1 meV左右；空穴超导能隙为2 meV，电子超导能隙为5 meV左右 [12] [13] [14] [15] 。通过将两片FeSeTe材料组合，可以在交界面形成超导拓扑表面态。本文通过平均场理论自洽地计算了该超导能隙在不同的化学势下随温度的变化关系。

2. FeTeSe薄膜界面

铜氧化物高温超导体和铁基高温超导体是目前仅有的两个非常规高温超导体 [16] [17] 。铜基和铁基高温超导体在结构上都是二维层状材料，由空间层和超导层沿着晶轴方向相互堆叠而成 [18] 。因此，二维层状材料成为人们探索新型高温超导材料的热点 [19] 。本文的研究基于铁基超导，所用模型见图1。

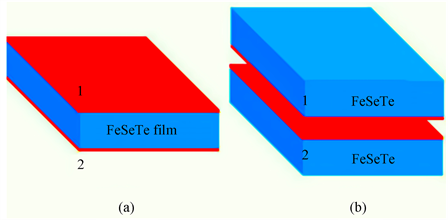
Figure 1. Superconducting topological surface states coupled in FeTeSe. In the figure, red is the surface state, and the blue region is the bulk state. (a) There are superconducting topological surface states at the top and bottom of the FeSeTe film. (b) Two topological surface-state superconductors with opposite surfaces

图1. 在FeTeSe材料中耦合的超导拓扑表面态。图中红色为表面态，蓝色区域为体态。(a) 表示FeSeTe薄膜的顶部和底部有超导拓扑表面态。(b) 表示两个有着相反表面的拓扑表面态超导体

3. BCS理论的平均场自洽求解

$H=H_{sp}+H_p$ (1)

$H_{sp}={\displaystyle \underset{k}{\sum }{\epsilon }_k}\left(C_k^{†}{C}_k+C_{-k}^{†}{C}_{-k}\right),H_p=-V{\displaystyle \underset{k,k^{\prime }>k_F}{\sum }{C}_{k^{\prime }}^{†}{C}_{-k^{\prime }}^{†}{C}_{-k}{C}_k}$ (2)

将对相互作用项 $H_p$ 中的对算子 $C_{-k}{C}_k$ 及 $C_{k^{\prime }}^{†}{C}_{-k^{\prime }}^{†}$ 用其在超导基态下的平均量代替来平均场化哈密顿量

$H_p=-V{\displaystyle \underset{k,k^{\prime }>k_F}{\sum }{C}_{k^{\prime }}^{†}{C}_{-k^{\prime }}^{†}}\langle C_{-k}{C}_k\rangle +\langle C_{k^{\prime }}^{†}{C}_{-k^{\prime }}^{†}\rangle C_{-k}{C}_k$ (3)

将H写成BdG形式：

$H={\Psi }_N^{†}h{\Psi }_N=\left(\begin{array}{cc}{C}_k^{†}& C_{-k}\end{array}\right)\left(\begin{array}{cc}{\epsilon }_k& -V\underset{k}{{\displaystyle \sum }}\langle C_{-k}{C}_k\rangle \\ -V\underset{k}{{\displaystyle \sum }}\langle C_k^{†}{C}_{-k}^{†}\rangle & -{\epsilon }_k\end{array}\right){\left(\begin{array}{cc}{C}_k& C_{-k}^{†}\end{array}\right)}^{\text{T}}$ (4)

令

$\Delta =V\underset{k}{{\displaystyle \sum }}\langle C_{-k}{C}_k\rangle$ (5)

考虑 $\Delta$ 为实量，则：

$H=\left(\begin{array}{cc}{C}_k^{†}& C_{-k}\end{array}\right)\left(\begin{array}{cc}{\epsilon }_k& -\Delta \\ -\Delta & -{\epsilon }_k\end{array}\right){\left(\begin{array}{cc}{C}_k& C_{-k}^{†}\end{array}\right)}^{\text{T}}$ (6)

进行粒子–准粒子变换(Bogoliubov-Valatin)简化为无相互作用的准粒子体系

$H={\Psi }_N^{†}U{U}^{†}hU{U}^{†}{\Psi }_N={\varphi }_N^{†}{E}_N{\varphi }_N,{\Psi }_N=U{\varphi }_N$ (7)

其中 $E_N$ 为准粒子能量， ${\varphi }_N$ 为准粒子算符

得

${\left(\begin{array}{cc}{C}_k& C_{-k}^{†}\end{array}\right)}^{\text{T}}={\left(\begin{array}{cc}u{\alpha }_k+v{\alpha }_{-k}^{†}& -v{\alpha }_k+u{\alpha }_{-k}^{†}\end{array}\right)}^{\text{T}}$ (8)

$\left(\begin{array}{cc}{C}_k^{†}& C_{-k}\end{array}\right)=\left(\begin{array}{cc}u{\alpha }_k^{†}+v{\alpha }_{-k}& -v{\alpha }_k^{†}+u{\alpha }_{-k}\end{array}\right)$ (9)

结合(8)，(9)，(5)式

$\Delta =V\underset{k}{{\displaystyle \sum }}\langle C_{-k}{C}_k\rangle$

${\left(\begin{array}{cc}{C}_k& C_{-k}^{†}\end{array}\right)}^{\text{T}}={\left(\begin{array}{cc}u{\alpha }_k+v{\alpha }_{-k}^{†}& -v{\alpha }_k+u{\alpha }_{-k}^{†}\end{array}\right)}^{\text{T}}$

$\left(\begin{array}{cc}{C}_k^{†}& C_{-k}\end{array}\right)=\left(\begin{array}{cc}u{\alpha }_k^{†}+v{\alpha }_{-k}& -v{\alpha }_k^{†}+u{\alpha }_{-k}\end{array}\right)$

得到：

$\begin{array}{c}\Delta =V\underset{k}{{\displaystyle \sum }}\langle \left(-v{\alpha }_k^{†}+u{\alpha }_{-k}\right)\left(u{\alpha }_k+v{\alpha }_{-k}^{†}\right)\rangle \\ =V\underset{k}{{\displaystyle \sum }}\langle 0|u{\alpha }_{-k}v{\alpha }_{-k}^{†}|0\rangle \\ =V{\displaystyle \underset{k}{\sum }uv}\end{array}$

求解久期方程，将结果代入上式中得到 $\Delta$ 的自洽方程

$\Delta =\frac{1}{2}V\underset{k}{{\displaystyle \sum }}\frac{\Delta }{\sqrt{{\epsilon }_k^2+{\Delta }^2}}$ (10)

对该方程进行自洽求解后可以得到零温能隙 $\Delta \left(0\right)=1.3476\times {10}^{-4}\text{eV}$ 。能隙随温度的变化关系见图2：

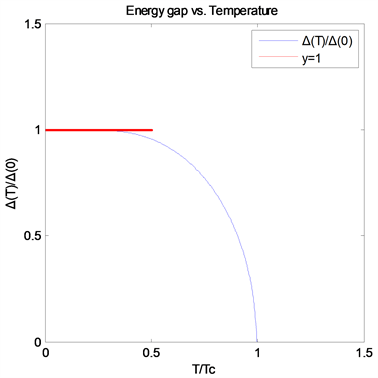
Figure 2. The energy gap changes with temperature. Near zero temperature, the energy gap decreases slowly, and the two curves almost coincide. Near the superconducting transition temperature, the energy gap decreases sharply, indicating that the superconducting state is rapidly changing to the trivial state

图2. 能隙随温度的变化曲线，在零温附近，能隙降低的速度很慢，两曲线几乎重合。在超导转变温度T_c附近，能隙急剧变小，表示超导态在迅速向平庸态转变

4. 超导拓扑表面态能隙的平均场自洽求解

所用模型的哈密顿量h可写成一8 × 8的矩阵：

$\left(\begin{array}{cccccccc}\lambda -\mu & q_1-i\ast q_2& T& 0& 0& -\Delta & 0& {\Delta }_s+{\Delta }_t\\ q_1+i\ast q_2& -\lambda -\mu & 0& T& \Delta & 0& -{\Delta }_s+{\Delta }_t& 0\\ T& 0& \lambda -\mu & -q_1+i\ast q_2& 0& {\Delta }_s-{\Delta }_t& 0& \Delta \\ 0& T& -q_1-i\ast q_2& -\lambda -\mu & -{\Delta }_s-{\Delta }_t& 0& -\Delta & 0\\ 0& \Delta & 0& -{\Delta }_s-{\Delta }_t& -\lambda +\mu & q_1+i\ast q_2& -T& 0\\ -\Delta & 0& {\Delta }_s-{\Delta }_t& 0& q_1-i\ast q_2& \lambda +\mu & 0& -T\\ 0& -{\Delta }_s+{\Delta }_t& 0& -\Delta & -T& 0& -\lambda +\mu & -q_1-i\ast q_2\\ {\Delta }_s+{\Delta }_t& 0& \Delta & 0& 0& -T& -q_1+i\ast q_2& \lambda +\mu \end{array}\right)$

其中q指标表示为动量，T是上下表面间的跃迁常数， $\lambda$ 为塞曼项， $\mu$ 表示化学势， $\Delta$ 为表面内自旋单态配对常数， ${\Delta }_s$ 和 ${\Delta }_t$ 分别为表面间自旋单态配对强度和表面间自旋三重态配对常数。

4.1. 能谱

将矩阵进行块对角化后得到：

$h=\left(\begin{array}{cccccccc}-t& q_1+i{q}_2& 0& \Delta +{\Delta }_t& 0& 0& 0& 0\\ q_1-i{q}_2& t& -\Delta -{\Delta }_t& 0& 0& 0& 0& 0\\ 0& -\Delta -{\Delta }_t& t& q_1-i{q}_2& 0& 0& 0& 0\\ \Delta +{\Delta }_t& 0& q_1+i{q}_2& -t& 0& 0& 0& 0\\ 0& 0& 0& 0& t& q_1+i{q}_2& 0& \Delta -{\Delta }_t\\ 0& 0& 0& 0& q_1-i{q}_2& -t& -\Delta +{\Delta }_t& 0\\ 0& 0& 0& 0& 0& -\Delta +{\Delta }_t& -t& q_1-i{q}_2\\ 0& 0& 0& 0& \Delta -{\Delta }_t& 0& q_1+i{q}_2& t\end{array}\right)$

同时得到本征谱见图3：

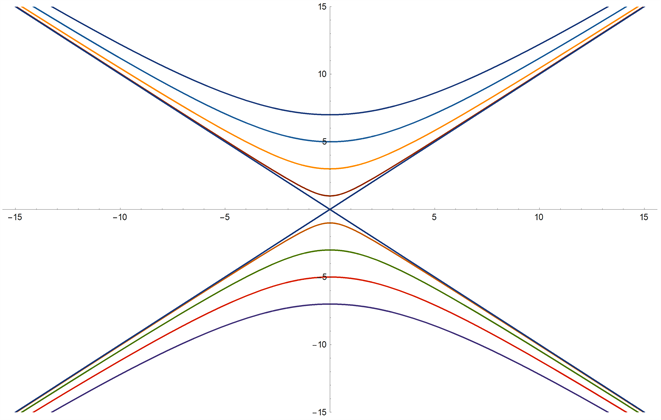
Figure 3. Eigenenergy spectrum, energy spectrum about zero energy symmetry

图3. 本征谱，关于零能对称的能谱

4.2. 平均场理论的方程推导

该哈密顿量的Nambu基为

${\Psi }_N={\left(\begin{array}{cccccccc}{\psi }_{1\uparrow q}& {\psi }_{1\downarrow q}& {\psi }_{2\uparrow q}& {\psi }_{2\downarrow q}& {\psi }_{1\uparrow \left(-q\right)}^{†}& {\psi }_{1\downarrow \left(-q\right)}^{†}& {\psi }_{2\uparrow \left(-q\right)}^{†}& {\psi }_{2\downarrow \left(-q\right)}^{†}\end{array}\right)}^{\text{T}}$ (11)

${\Psi }_T^{†}=\left(\begin{array}{cccccccc}{\psi }_{1\uparrow q}^{†}& {\psi }_{1\downarrow q}^{†}& {\psi }_{2\uparrow q}^{†}& {\psi }_{2\downarrow q}^{†}& {\psi }_{1\uparrow \left(-q\right)}& {\psi }_{1\downarrow \left(-q\right)}& {\psi }_{2\uparrow \left(-q\right)}& {\psi }_{2\downarrow \left(-q\right)}\end{array}\right)$ (12)

代入 $H={\Psi }^{†}h\Psi$ 中，按照平均场计算的方法，分别找到 $\Delta$ 及 ${\Delta }_t$ 相关项。得到：

$\Delta =\underset{q}{{\displaystyle \sum }}\langle {\psi }_{1\uparrow -q}^{†}{\psi }_{1\downarrow q}^{†}-{\psi }_{2\uparrow -q}^{†}{\psi }_{2\downarrow q}^{†}\rangle$ (13)

${\Delta }_t=V\underset{q}{{\displaystyle \sum }}\langle {\psi }_{2\downarrow -q}^{†}{\psi }_{1\uparrow q}^{†}-{\psi }_{1\downarrow -q}^{†}{\psi }_{2\uparrow q}^{†}\rangle$ (14)

进行粒子–准粒子变换(Bogoliubov-Valatin)后的基为：

$\Phi ={\left(\begin{array}{cccccccc}{\varphi }_{1\uparrow q}& {\varphi }_{1\downarrow q}& {\varphi }_{2\uparrow q}& {\varphi }_{2\downarrow q}& {\varphi }_{1\uparrow \left(-q\right)}^{†}& {\varphi }_{1\downarrow \left(-q\right)}^{†}& {\varphi }_{2\uparrow \left(-q\right)}^{†}& {\varphi }_{2\downarrow \left(-q\right)}^{†}\end{array}\right)}^{\text{T}}$ (15)

${\Phi }^{†}=\left(\begin{array}{cccccccc}{\varphi }_{1\uparrow q}^{†}& {\varphi }_{1\downarrow q}^{†}& {\varphi }_{2\uparrow q}^{†}& {\varphi }_{2\downarrow q}^{†}& {\varphi }_{1\uparrow \left(-q\right)}& {\varphi }_{1\downarrow \left(-q\right)}& {\varphi }_{2\uparrow \left(-q\right)}& {\varphi }_{2\downarrow \left(-q\right)}\end{array}\right)$ (16)

令本征矢矩阵为：

$U_1=\left(\begin{array}{cccccccc}-u_1& 0& u_3& 0& 0& u_6& 0& -u_8\\ -v_1& 0& v_3& 0& 0& v_6& 0& -v_8\\ v_1& 0& v_3& 0& 0& v_6& 0& v_8\\ u_1& 0& u_3& 0& 0& u_6& 0& u_8\\ 0& u_2& 0& -u_4& -u_5& 0& u_7& 0\\ 0& -v_2& 0& v_4& v_5& 0& -v_7& 0\\ 0& -v_2& 0& -v_4& -v_5& 0& -v_7& 0\\ 0& u_2& 0& u_4& u_5& 0& u_7& 0\end{array}\right)$

则可得：

$\begin{array}{c}\Delta =2V\underset{q}{{\displaystyle \sum }}\frac{1}{2}\left(-u_5^2+u_6^2+u_7^2-u_8^2\right)+\frac{1}{2}{f}_{{\xi }_k}\left(-u_1^2+u_2^2+u_3^2-u_4^2+u_5^2-u_6^2-u_7^2+u_8^2\right)\\ +\frac{1}{2}\left(-v_5^2-v_6^2+v_7^2+v_8^2\right)+\frac{1}{2}{f}_{{\xi }_k}\left(v_1^2+v_2^2-v_3^2-v_4^2+v_5^2+v_6^2-v_7^2-v_8^2\right)\end{array}$ (17)

及

$\begin{array}{c}{\Delta }_t=2V\underset{q}{{\displaystyle \sum }}\frac{1}{2}\left(-v_5^2-v_6^2+v_7^2+v_8^2\right)+\frac{1}{2}{f}_{{\xi }_k}\left(v_1^2+v_2^2-v_3^2-v_4^2+v_5^2+v_6^2-v_7^2-v_8^2\right)\\ +\frac{1}{2}\left(u_5+u_6-u_7-u_8\right)+\frac{1}{2}{f}_{{\xi }_k}\left(-u_1-u_2+u_3+u_4-u_5-u_6+u_7+u_8\right)\end{array}$ (18)

其中 $f_{{\xi }_k}$ 为费米分布函数。

4.3. 自洽计算

考虑 $\lambda =0$ ； ${\Delta }_s=0$ ； $T=0.5$ ； $\mu =1$ ；对 $\Delta$ 及 ${\Delta }_t$ 进行数值化自洽求解。首先将哈密顿量中其他量也给予一个初始数值用于迭代计算 $q_2=0.01$ ； $q_1=0.01$ ； $\mu =\text{1}$ ； $\Delta =1$ ； ${\Delta }_t=1$ ；得到如下数值化的哈密顿量矩阵：

$\left(\begin{array}{cccccccc}-1& 0.01-0.01i& 0.5& 0& 0& -1& 0& 2\\ 0.01+0.01i& -1& 0& 0.5& 1& 0& 2& 0\\ 0.5& 0& -1& -0.01+0.01i& 0& -2& 0& 1\\ 0& 0.5& -0.01-0.01i& -1& -2& 0& -1& 0\\ 0& 1& 0& -2& 1& 0.01+0.01i& -0.5& 0\\ -1& 0& -2& 0& 0.01-0.01i& 1& 0& -0.5\\ 0& 2& 0& -1& -0.5& 0& 1& -0.01-0.01i\\ 2& 0& 1& 0& 0& -0.5& -0.01+0.01i& 1\end{array}\right)$

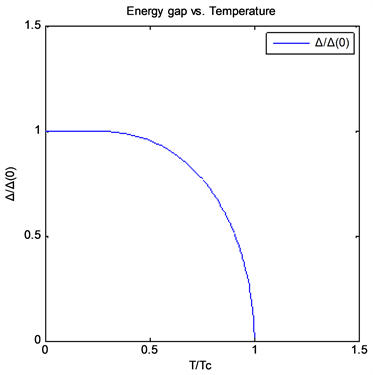
每一轮计算后，将新得到的值代入下一轮运算中。直到结果满足自洽计算的要求。最后得到 $\text{Δ}\left(0\right)=8.00106\times {10}^{-7}\text{eV}$ ， ${\Delta }_t\left(0\right)=4.00053\times {10}^{-6}\text{eV}$ 。能隙随温度的变化关系见图4：

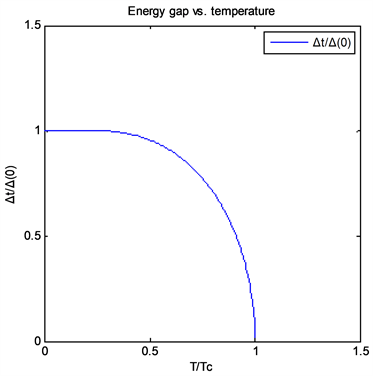(a) (b)

Figure 4. The temperature dependence of the band gap (a) is the intra-surface spin singlet pairing constant, and (b) is the inter-surface spin triplet pairing constant

图4. 能隙随温度的变化关系(a) 为表面内自旋单态配对常数，(b) 为表面间自旋三重态配对常数

5. 结论

计算表明，FeTeSe表面存在狄拉克锥形拓扑表面能带。当体能带打开超导间隙时，通过带间散射在表面带中诱导s波超导。由于其自旋螺旋结构，表面能带表现出拓扑超导电性，而体的超导电性是拓扑平庸的，这表明很容易产生马约拉纳边缘模。同时相对较高的超导转变温度以及单晶薄膜的生长容易使得FeSeTe成为研究Majorana束缚态的平台，并可能推进拓扑量子计算的研究。