非参数动态空间随机前沿模型的贝叶斯估计

Bayesian Estimation of Nonparametric Dynamic Spatial Stochastic Frontier Models

摘要: 空间随机前沿模型忽视了经济变量之间存在的非线性关系，限制了其使用范围。本文构建非参数动态空间随机前沿模型，利用贝叶斯方法估计该模型。数值模拟表明，多元B样条具有良好的拟合能力，模型的估计精度随样本量的增加而提高，无效率项方差的偏差表现不稳定。

Abstract: The spatial stochastic frontier model ignores the nonlinear relationship between economic varia-bles, which limits its scope of use. This article constructs a non parametric dynamic spatial sto-chastic frontier model and uses Bayesian methods to estimate the model. Numerical simulation shows that multivariate B-splines have good fitting ability, and the estimation accuracy of the model increases with the increase of sample size. The deviation of the variance of the invalidity term is unstable.

1. 引言

随机前沿分析法是测算技术效率的一种参数模型，该模型在实证方面有着广泛使用，主要应用于农业、工业、金融行业等产业的技术效率测算，技术效率反映了决策单元对现有资源有效利用的能力。随机前沿模型为各行各业调整投入决策，实现产出最大化提供科学依据。

Aigner等 [1] 首先提出随机前沿分析法，自该方法被提出，学术界在该模型的构建与估计方面有着丰富的研究成果，已有学者对面板随机前沿模型进行梳理，如边文龙和王向楠 [2] 从效率是否时变的角度总结了面板数据随机前沿模型的研究结果；王韧和李志伟 [3] 从误差分布、时变特征和模型形式等方面梳理面板随机前沿模型的历史演变和发展。目前，空间随机前沿模型是随机前沿模型中的研究热点，许多学者对空间随机前沿模型的构建与估计做研究，如于倩倩等 [4] 构建了地理加权随机前沿模型；Simwaka [5] 提出考虑误差项空间相关性与时间相关性的空间面板随机前沿模型；林显佳 [6] 构建了考虑空间滞后因变量和空间误差自相关的三种不同形式的空间随机前沿模型，包含截面模型和面板模型，且每个模型均有三个不同无效率项分布假设；蒋青嬗等 [7] 构建了考虑个体固定效应的真实固定效应空间随机前沿模型；Tsukamoto [8] 构建了空间自回归面板随机前沿模型；蒋青嬗和李毅君 [9] 从技术效率时变和非时变两个层面分别构建空间门限随机前沿模型；任燕燕等 [10] 提出动态面板数据空间随机前沿模型并使用广义矩估计方法解决模型的内生性，但假设无效率不随时间变化，在研究对象的时间跨度较长时，该假设不符合实际情况。总的来说，关于随机前沿模型的文献不计其数，但少有文献研究生产函数错误假设的问题，即生产函数不含非线性函数，默认了各经济变量之间的关系是线性的，然而，现实生活中各经济变量之间不仅存在线性关系也存在大量的非线性关系，生产函数形式设定不正确将导致技术效率估计有偏不一致。

在生产函数错误假设问题的研究中，学者们认为应当放宽生产函数的假设形式，考虑利用非参数估计方法来解决此类问题，如Kumbhakar等 [11] 认为随机前沿模型的形式或者单边误差的分布假设是错误的，提出了基于局部极大似然技术的处理非参数随机前沿模型的新方法；Assaf等 [12] 认为生产函数不一定代表真正的前沿技术，构建非参数随机前沿模型并使用张量积傅里叶基拟合未知生产函数，但Kumbhakar等 [11] 和Assaf等 [12] 的非参数随机前沿模型不考虑空间效应，模型中的所有决策单元相互独立，这违背了地理学第一定律，将导致技术效率的测度结果存在较大偏误。蒋青嬗等 [13] [14] 构建一个同时包含随机前沿模型和回归模型的半参数空间零无效率随机前沿模型，模型引入空间效应和非参数模型，即生产函数由线性部分和非线性部分共同组成，然而非参数模型只允许有一个输入变量。

综上所述，虽有许多文献各自弥补了模型的一个不足之处，但少有在空间随机前沿模型中考虑生产函数形式错误假设的问题研究，当研究的问题存在前后相互关联的关系且研究内容的时间跨度较长时，静态模型不能很好地进行客观拟合分析，非时变无效率项也不能反应实际情况，因此，研究具有时变效率的非参数动态随机前沿模型具有实际意义。相比于极大似然估计法，贝叶斯估计方法在函数推导方面较为简便，且因复合误差项的非对称性，模型采用贝叶斯估计的效果比最小二乘法的好。鉴于此，本文构建非参数动态空间随机前沿模型，允许无效率项时变，通过多元B样条逼近未知生产函数，利用贝叶斯估计实现模型估计。本文首先介绍了非参数动态空间随机前沿模型的一般形式及其相关假设，其次给出了模型的条件后验分布、参数抽样过程和模型估计精度评估方法，最后对模型进行数值模拟。

2. 基本模型及假设

模型的一般形式设计如下：

$Y_{it}={\lambda }_1{\displaystyle \underset{i^{\prime }=1}{\overset{N}{\sum }}{w}_{i{i}^{\prime }}{Y}_{i^{\prime }t}}+{\lambda }_2{\displaystyle \underset{i^{\prime }=1}{\overset{N}{\sum }}{w}_{i{i}^{\prime }}}{Y}_{i^{\prime },t-1}+\gamma Y_{i,t-1}+F\left(x_{it},\beta \right)+v_{it}-u_{it}$ (1)

其中， $i=1,\cdots ,N$ ， $t=1,\cdots ,T$ ， $Y_{it}$ 为t时刻第i个生产单元的产出指标； $F\left(x_{it},\beta \right)$ 是一个未知函数， $w_{i{i}^{\prime }}$ 是空间权重矩阵元素，表示生产单元i和生产单元 $i^{\prime }$ 的空间相关关系， $x_{it}=\left[x_{1,it},\cdots ,x_{j,it},\cdots ,x_{K,it}\right]$ 表示为t时刻第i个生产单元的K个投入指标，式(1)中假设 $v_{it}~i.i.d.N\left(0,{\sigma }_v^2\right)$ ， $u_{it}~i.i.d.N^{+}\left(0,{\sigma }_u^2\right)$ ，且用如下线性组合估计未知函数：

$F\left(n_r,\beta \right)={\beta }_0+{\displaystyle \underset{k=1}{\overset{n_r}{\sum }}{B}_k\left(x_{it}\right){\beta }_k}=B\left(x_{it}\right)\beta$ (2)

$B_k\left(x_{it}\right)={\displaystyle \underset{j=1}{\overset{K}{\prod }}{\bar{B}}_{k,j}\left(x_{j,it}\right)}$ (3)

其中， $n_r=1+q+r_s$ ， $n_r\in \left[1,\infty \right)$ ， $s=1,\cdots ,S$ ， $r_s$ 为某一可能组合的样条张量积的节点数，S表示K个投入指标所有可能组合的数量。 $B\left(x_{it}\right)=\left[1,B_1\left(x_{it}\right),\cdots ,B_k\left(x_{it}\right),\cdots ,B_{n_r}\left(x_{it}\right)\right]$ 为多元B样条基向量， ${\bar{B}}_{k,j}\left(x_{j,it}\right)$ 为q阶B样条函数。系数向量 $\beta ={\left[{\beta }_0,{\beta }_1,\cdots ,{\beta }_k,\cdots ,{\beta }_{n_r}\right]}^{\prime }$ 服从多元正态分布，即 $\beta ~N\left(\mu ,{\sigma }_v^2\tau \Lambda \right)$ ，Λ为正定矩阵。

式(1)可以用矩阵形式如下：

$Y_t={\lambda }_{1}w{Y}_t+{\lambda }_{2}w{Y}_{t-1}+\gamma Y_{t-1}+B\left(x_t\right)\beta +v_t-u_t$ (4)

其中， $Y_t={\left[Y_{1t}\cdots Y_{Nt}\right]}^{\prime }$ ， $Y_{t-1}={\left[Y_{1,t-1}\cdots Y_{N,t-1}\right]}^{\prime }$ ， $v_t={\left[v_{1t}\cdots v_{Nt}\right]}^{\prime }$ ， $u_t={\left[u_{1t}\cdots u_{Nt}\right]}^{\prime }$ 均为N维向量，w为 $N\times N$ 阶的空间距离矩阵， $B\left(x_t\right)$ 为 $N\times \left(n+1\right)$ 的样条基矩阵，具体如下：

$B\left(x_t\right)={\left[\begin{array}{c}B\left(x_{1t}\right)\\ ⋮\\ B\left(x_{it}\right)\\ ⋮\\ B\left(x_{Nt}\right)\end{array}\right]}_{N\times 1}={\left[\begin{array}{cc}\begin{array}{c}1\\ ⋮\\ 1\\ ⋮\\ 1\end{array}& \begin{array}{ccccc}{B}_1\left(x_{1t}\right)& \cdots & B_k\left(x_{1t}\right)& \cdots & B_n\left(x_{1t}\right)\\ ⋮& & ⋮& & ⋮\\ B_1\left(x_{it}\right)& \cdots & B_k\left(x_{it}\right)& \cdots & B_n\left(x_{it}\right)\\ ⋮& & ⋮& & ⋮\\ B_1\left(x_{Nt}\right)& \cdots & B_k\left(x_{Nt}\right)& \cdots & B_n\left(x_{Nt}\right)\end{array}\end{array}\right]}_{N\times \left(n+1\right)}$ (5)

若令 $A\left({\lambda }_1\right)=I_N-{\lambda }_{1}w$ ， $C\left({\lambda }_2,\gamma \right)={\lambda }_{2}w+\gamma I_N$ ， $I_N$ 为N阶单位矩阵，则式(4)转变为如下式(6)：

$A\left({\lambda }_1\right)Y_t-C\left({\lambda }_2,\gamma \right)Y_{t-1}-B\left(x_t\right)\beta +u_t=v_t$ (6)

其中， $u_t~N^{+}\left(0,{\sigma }_u^2{I}_N\right)$ ， $v_t~N\left(0,{\sigma }_v^2{I}_N\right)$ 。

3. 模型的贝叶斯估计

3.1. 参数的先验分布假设

将无效率项视为未知参数，模型的未知参数为 $\theta =\left({\lambda }_1,{\lambda }_2,\gamma ,f\left(n_r,\beta \right),{\sigma }_v^2,{\sigma }_u^2,u_t\right)$ ，对样条基系数 $\beta$ 的分布假设参考了Yoo等 [15] 的处理方式，节点个数 $r_s$ 服从泊松分布，其他未知参数参考蒋青嬗等 [7] 、任燕燕等 [10] 文章中关于模型参数的分布假设，本文对所有未知参数的假设如下：

$\gamma ~U\left(-1,1\right)$ ， $\beta ~N\left(\mu ,{\sigma }_v^2\tau \Lambda \right)$ ， ${\lambda }_1~U\left(\frac{1}{{\lambda }_{\min }},\frac{1}{{\lambda }_{\max }}\right)$ ， ${\lambda }_2~U\left(\frac{1}{{\lambda }_{\min }},\frac{1}{{\lambda }_{\max }}\right)$ ，

${\sigma }_v^2~IG\left(\frac{a_v}{2},\frac{b_v}{2}\right)$ ， ${\sigma }_u^2~IG\left(\frac{a_u}{2},\frac{b_u}{2}\right)$ ， $r_s~P\left({\lambda }_s\right)$ ，

其中， ${\lambda }_{\text{min}}$ 和 ${\lambda }_{\max }$ 分别是空间权重矩阵 $w$ 的最小和最大特征值。

3.2. 条件后验分布

由复合误差项的分布假设和式(6)，可得到随机误差项 $v_t$ 的概率密度函数如下：

$p\left(v_t\right)={\left(2\pi {\sigma }_v^2\right)}^{-\frac{N}{2}}\cdot \left|A\left({\lambda }_1\right)\right|\cdot \exp \left\{-\frac{{v^{\prime }}_t{v}_t}{2{\sigma }_v^2}\right\}$ (7)

则 $Y_t$ 和 $u_t$ 的联合密度函数：

$f\left(Y_t,u_t\right)\propto {\left({\sigma }_v^2\right)}^{-\frac{NT}{2}}\cdot {\left({\sigma }_u^2\right)}^{-\frac{NT}{2}}\cdot \left|A\left({\lambda }_1\right)\right|\cdot \exp \left\{-\frac{{\displaystyle {\sum }_{t=1}^T{v^{\prime }}_t{v}_t}}{2{\sigma }_v^2}-\frac{{\displaystyle {\sum }_{t=1}^T{u^{\prime }}_t{u}_t}}{2{\sigma }_u^2}\right\}$ (8)

由联合分布函数和先验分布可得到联合后验分布，从联合后验分布中推导出各参数后验分布，简记 $A=A\left({\lambda }_1\right)$ ， $C=C\left({\lambda }_2,\gamma \right)$ ，各参数将分别从以下对应的分布函数中抽样：

$\pi \left(u_t|{\theta }_{-(u_t)},Y_t\right)~N^{+}\left(\hat{u},\Omega \right)$ (9)

$\pi \left(\beta |{\theta }_{-(\beta )},Y_t\right)~N\left(\hat{\beta },{\sigma }_v^2\Sigma \right)$ (10)

$\pi \left({\sigma }_u^2|{\theta }_{-({\sigma }_u^2)},Y_t\right)~IG\left(\frac{NT+a_u}{2},\frac{b_u+{\displaystyle {\sum }_{i=1}^T{u^{\prime }}_t{u}_t}}{2}\right)$ (11)

$\pi \left({\sigma }_v^2|{\theta }_{-({\sigma }_v^2)},Y_t\right)~IG\left(\frac{NT+a_v}{2},\frac{{\displaystyle {\sum }_{t=1}^T{v^{\prime }}_t{v}_t+b_v}}{2}\right)$ (12)

$\pi \left(\gamma |{\theta }_{-(\gamma )},Y_t\right)~N\left(\frac{{\displaystyle {\sum }_{t=1}^T{\left(A{Y}_t-B\left(x_t\right)\beta +u_t-{\lambda }_{2}w{Y}_{t-1}\right)}^{\prime }{Y}_{t-1}}}{{\displaystyle {\sum }_{t=1}^T{Y^{\prime }}_{t-1}{Y}_{t-1}}},\frac{{\sigma }_v^2}{{\displaystyle {\sum }_{t=1}^T{Y^{\prime }}_{t-1}{Y}_{t-1}}}\right)$ (13)

$\pi \left({\lambda }_2|{\theta }_{-({\lambda }_2)},Y_t\right)~N\left(\frac{{\displaystyle {\sum }_{t=1}^T{\left(A{Y}_t-B\left(x_t\right)\beta +u_t-\gamma Y_{t-1}\right)}^{\prime }\left(w{Y}_{t-1}\right)}}{{\displaystyle {\sum }_{t=1}^T{\left(w{Y}_{t-1}\right)}^{\prime }\left(w{Y}_{t-1}\right)}},\frac{{\sigma }_v^2}{{\displaystyle {\sum }_{t=1}^T{\left(w{Y}_{t-1}\right)}^{\prime }\left(w{Y}_{t-1}\right)}}\right)$ (14)

$\pi \left({\lambda }_1|{\theta }_{-({\lambda }_1)},Y_t\right)\propto \left|I_N-{\lambda }_{1}w\right|\cdot \exp \left\{-\frac{{\displaystyle {\sum }_{t=1}^T{\left(w{Y}_t\right)}^{\prime }w{Y}_t}}{2{\sigma }_v^2}{\lambda }_1{}^2+\frac{{\displaystyle {\sum }_{t=1}^T{v^{\prime }}_{t}w{Y}_t}}{{\sigma }_v^2}{\lambda }_1\right\}$ (15)

$\pi \left(r|{\theta }_{(-n)},Y_t\right)\propto {\displaystyle \underset{s}{\overset{S}{\prod }}\frac{{\lambda }^{r_s}}{r_s!}}\exp \left\{\frac{{\displaystyle {\sum }_{t=1}^T{\left(A{Y}_t-C{Y}_{t-1}+u_t\right)}^{\prime }B\left(x_t\right)\beta }}{{\sigma }_v^2}-\frac{{\displaystyle {\sum }_{t=1}^T{\left(B\left(x_t\right)\beta \right)}^{\prime }B\left(x_t\right)\beta }}{2{\sigma }_v^2}\right\}$ (16)

其中， $\hat{u}=-{\sigma }_u^2{\epsilon }_t/{\sigma }_v^2{\sigma }_u^2$ ； $\Omega =\left({\sigma }_v^2{\sigma }_u^2/\left({\sigma }_u^2+{\sigma }_v^2\right)\right)I$ ； $\hat{\beta }=\Sigma \left[B\left(x_t\right)\left(A{Y}_t-C{Y}_{t-1}+u_t\right)+{\left(\tau \Lambda \right)}^{-1}\mu \right]$ ； $\Sigma ={\left[B^{\prime }\left(x_t\right)B\left(x_t\right)+{\left(\tau \Lambda \right)}^{-1}\right]}^{-1}$ 。

3.3. 参数抽样

从以上所得到的参数条件后验分布可知，参数 $\left({\lambda }_2,\gamma ,\beta ,{\sigma }_v^2,{\sigma }_u^2,u_t\right)$ 的抽样可通过Gibbs抽样来完成，参数 $n_r$ ， ${\lambda }_1$ 可通过MH方法进行抽样。对参数 $\theta =\left({\lambda }_1,{\lambda }_2,\gamma ,f\left(n_r,\beta \right),{\sigma }_v^2,{\sigma }_u^2,u_t\right)$ 的抽样过程可整理为以下5个步骤：

1) 对所有参数赋予初值，记为 ${\theta }^0=\left({\lambda }_1^0,{\lambda }_2^0,{\gamma }^0,{\beta }^0,n_r^0,{\left({\sigma }_v^2\right)}^0,{\left({\sigma }_u^2\right)}^0,u_t^0\right)$ ；

2) 给定参数的初值 ${\theta }^0=\left({\lambda }_1^0,{\lambda }_2^0,{\gamma }^0,{\beta }^0,{\left({\sigma }_v^2\right)}^0,{\left({\sigma }_u^2\right)}^0,u_t^0\right)$ ，通过MH算法来更新参数 $n_r$ ，记更新后的值为 $n_r^1$ ；

3) 给定参数 $\left(n_r^1,{\left({\sigma }_v^2\right)}^0,{\left({\sigma }_u^2\right)}^0,{\lambda }_1^0,{\lambda }_2^0,{\gamma }^0,u_t^0\right)$ 的值，通过Gibbs算法来更新参数 $\beta$ ，记更新后的值为 ${\beta }^1$ ，根据 $n_r^1$ 和 ${\beta }^1$ 即可获得 $f^1\left(n_r,\beta \right)$ ；

4) 给定参数 $\left(n_r^1,{\beta }^1,{\left({\sigma }_v^2\right)}^0,{\left({\sigma }_u^2\right)}^0,{\lambda }_2^0,{\gamma }^0,u_t^0\right)$ 的值，通过MH算法来更新参数 ${\lambda }_1$ ，记更新后的值为 ${\lambda }_1^1$ ；

5) 给定参数 $\left(n_r^1,{\beta }^1,{\lambda }_1{}^1,{\gamma }^0,{\left({\sigma }_u^2\right)}^0,{\left({\sigma }_v^2\right)}^0,u_t^0\right)$ 的值，通过Gibbs算法来更新参数 ${\lambda }_2$ ，记更新后的值为 ${\lambda }_2^1$ ；同理更新 $\left(\gamma ,{\sigma }_u^2,{\sigma }_v^2,u_t\right)$ ，更新后的值记为 $\left({\gamma }^1,{\left({\sigma }_u^2\right)}^1,{\left({\sigma }_v^2\right)}^1,u_t^1\right)$ 这样便完成了从初始状态 ${\theta }^0=\left({\lambda }_1^0,{\lambda }_2^0,{\gamma }^0,{\beta }^0,n_r^0,{\left({\sigma }_v^2\right)}^0,{\left({\sigma }_u^2\right)}^0,u_t^0\right)$ 转移到下一个状态 ${\theta }^1=\left(n_r^1,{\beta }^1,{\gamma }^1,{\lambda }_2^1,{\lambda }_1^1,{\left({\sigma }_u^2\right)}^1,{\left({\sigma }_v^2\right)}^1,u_t^1\right)$ ，然后再以 ${\theta }^1$ 代替初值，重复进行步骤1至步骤5直到收敛，最后用后验样本均值来估计所有参数。

从M次迭代中取最后的M/3个观测值数据，计算各参数 $\left({\lambda }_1,{\lambda }_2,\gamma ,{\sigma }_v^2,{\sigma }_u^2\right)$ 的平均值作为参数估计值，计算 $f\left(n_r,\beta \right)$ 的均值作为非参数模型估计值。

3.4. 数值模拟评估方法

考察参数 $\left({\lambda }_1,{\lambda }_2,\gamma ,{\sigma }_v^2,{\sigma }_u^2\right)$ 的标准差、偏差、均方误差和平均绝对误差。考察非参数模型 $f\left(n_r,\beta \right)$ 的均方误差、平均绝对误差和拟合优度。同时，为观察非参数模型估计值与真实值的数据分布情况，给出对应的核密度曲线图。标准差、偏差、均方误差、平均绝对误差越小，模型估计精度越高，非参数模型估计值与真实值之间的核密度曲线越贴近则估计精度越高。

4. 数值模拟

对所建模型进行数值模拟。设计2组模拟：

1) 模拟一：

样本量为 $\left\{TN=100\right\}$ ，被解释变量数量为1，解释变量数量为2，数值均由均匀分布 $U\left(0,1\right)$ 产生。对于非参数模型，阶数 $q=2$ ，系数 $\beta$ 的先验分布中超参数 $\tau ={10}^4$ ， $\mu =0$ 。误差的后验分布超参数 $a_v=a_u=8$ ， $b_u=b_v=2$ 。空间权重矩阵为对角线上为零的0-1对称矩阵，矩阵大小为 $N\times N$ ，为减少区域间的外生影响对空间权重矩阵标准化。假设模型中生产函数形式如下：

$F_1\left(x_t,\beta \right)=2\ln \left(x_{1,t}\right)+2\ln \left(x_{2,t}\right)+0.3\ln \left(x_{1,t}\right)\ln \left(x_{2,t}\right)+0.3{\ln }^2\left(x_{2,t}\right)+0.2{\ln }^2\left(x_{2,t}\right)$ (17)

2) 模拟二：

样本量为 $\left\{TN=200\right\}$ ，其他设定与模拟一相同。

两组模拟分别产生符合上述假设的数据用于数值模拟，模拟迭代1000次，取最后1000/3个观测值的平均值作为参数估计。非参数动态空间随机前沿模型的估计精度结果详见表1。

据表1所示：模型的估计量精度较高，总体上模型的估计精度随样本量的增加而提高，但参数 ${\sigma }_u^2$ 的偏差表现不稳定。当样本量为200时，参数 ${\sigma }_u^2$ 的偏差和均方误差均高于样本量为100时的，但参数 ${\sigma }_u^2$ 的标准差和平均绝对误差比样本量为100时的低，表明 ${\sigma }_u^2$ 估计量的偏差表现不稳定。当样本量为200时，其余参数 $\left\{{\lambda }_1,{\lambda }_2,\gamma ,{\sigma }_v^2\right\}$ 的标准差、偏差、均方误差和平均绝对误差均比样本量为100时的低，非参数模型 $f\left(n_r,\beta \right)$ 的均方误差和平均绝对误差均比样本量为100时的低，其拟合优度比样本量为100时的高，表明参数 $\left\{{\lambda }_1,{\lambda }_2,\gamma ,f\left(n_r,\beta \right),{\sigma }_v^2\right\}$ 的估计精度随样本量增加而提升。

从核密度曲线图上看，多元B样条具有良好的拟合能力。以下展示两组数值模拟中非参数模型 $f\left(n_r,\beta \right)$ 的核密度曲线图。图1(a)和图1(b)分别展示了模拟一和模拟二中非参数模型的核密度曲线图，其中， $pre\_f$ 为非参数模型， $ture\_f$ 为真实生产函数，核密度曲线越靠近则估计精度越高。

Table 1. Estimation accuracy results of nonparametric dynamic space stochastic frontier model

表1. 非参数动态空间随机前沿模型的估计精度结果

注：结果展示将标准差、偏差、均方误差、平均绝对误差和拟合优度五个指标依次上下排列。

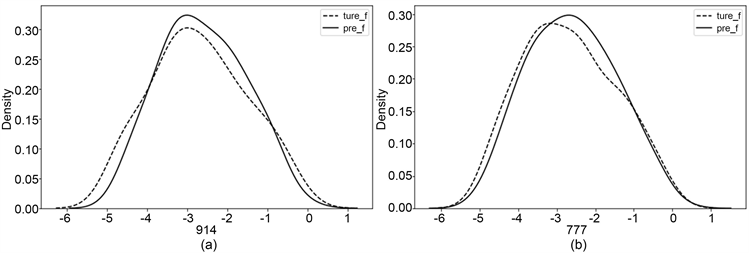
Figure 1. Kernel density estimation plots of non-parametric models in Simulation 1 and Simulation 2

图1. 模拟一和模拟二的中非参数模型的核密度估计图

5. 总结

本文构建一个非参数动态空间随机前沿模型，利用多元B样条逼近未知生产函数，运用贝叶斯方法对该模型进行估计，数值模拟表明：多元B样条具有良好的拟合能力，模型的估计精度随样本量的增加而提高，无效率项方差的偏差表现不稳定。非参数动态空间随机前沿模型放松了生产函数为线性关系的假设条件，拓宽了随机前沿模型的使用范围。