1. 引言
特征值问题广泛地应用于科学和工程领域,如量子力学,流体力学和随机过程 [1] [2] [3] [4] [5] 等。其数值计算方法一直备受很多学者关注。因此,提出一些有效求解特征值问题的高精度数值方法是非常有意义的。
到目前为止,已经有一些有限元法 [6] [7] [8] ,有限差分法 [9] [10] [11] 相继被提出并应用于求解特征值问题。然而,这些数值方法要获得高精度的数值解需要花费大量计算时间和内存容量。众所周知,目前很少有将谱方法应用于求解基于混合格式的四阶特征值问题。因此,本文提出了四阶特征值问题基于降阶格式的一种有效的Legendre-Galerkin逼近。首先,我们引入了一个辅助函数,将原问题转化为一个二阶混合格式。通过引入一些适当的Sobolev空间,其相应的变分形式被建立,并在解足够光滑条件下证明了其等价性。其次,基于Legendre多项式的正交性质,两组紧凑的基函数被构造,并导出具有稀疏系数矩阵的线性特征系统。最后,我们给出了两个数值例子,数值结果表明了算法的收敛性与高精度。
本文其余部分组织如下:在第2节,我们推导了四阶特征值问题等价的二阶耦合格式及其变分形式。在第3节,我们给出了算法的有效实现。第4节,我们给出了一些数值例子。第5节,我们给出了结论性注记。
2. 耦合的降阶格式及其变分形式
本文考虑如下的四阶特征值问题:
(1)
其中
为非负常数,
为
中的有界区域,
表示单位外法向量。
令
,则方程组(1)等价于如下的二阶混合格式:
(2)
令
,
和
为通常的Sobolev空间,
和
分别为
和
或
中的范数,
为
或
中的半范数。记
则 的弱形式为:求
使得:
(3)
不失一般性,我们仅考虑
的情况。设
为区间
上的N次多项式空间,定义逼近空间
和
,则(3)式的离散格式为:求
使得:
(4)
定理1:四阶特征值问题(1)与混合变分问题(3)等价。
证明:若
为(1)的解,由格林公式可知
为(3)的解。反之,若
为(3)的解,则对
,由格林公式可得:
将上式代入(3)的第二个等式可得:
由变分法基本引理可得:
(5)
类似地,由格林公式,变分法基本引理和(3)的第一个等式可得:
(6)
另一方面,对于
,由(3)的第一个等式可得:
(7)
在(7)中取
,结合(6)可得:
。再将(6)代入(5)可知
为(1)的解。证毕。
3. 算法的有效实现
在这节,我们将详细描述算法的实现过程。首先构造逼近空间中的一组基函数,我们用
表示n次Legendre多项式。令
则有
记
令
用
表示由W的列构成的长度为
的列向量。用
表示由
的列构成的长度为
的列向量,则对
我们有
其中
,
表示矩阵
的第m行,
表示矩阵的张量积,即
。记
因此(4)等价于下面的矩阵形式:
4. 数值例子
在这一节,我们将在MATLAB R2017a平台上进行两个数值例子,通过数值结果来验证我们提出的算法是一种高精度数值方法。
例1:我们的第一个算例取
,
,用第3节提出的算法求解问题(1),对于不同的N,我们在表1中列出了前4个特征值的数值结果(
为重根)。另外,我们以
时的数值解作为一个参考解,并在图1中列出了
关于不同的N的误差曲线。

Table 1. For different N, the first four approximate eigenvalue numerical results
表1. 对于不同的N,前4个逼近特征值的数值结果
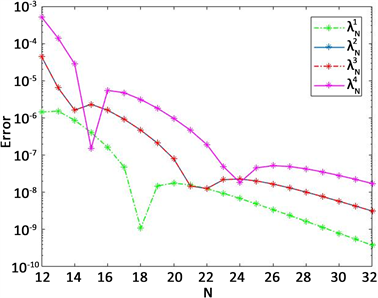
Figure 1. The error between the approximation eigenvalue
and the reference solution
图1. 逼近特征值
与参考解之间的误差
从表1和图1中可以观察到我们的算法是收敛的和高精度的。
例2:我们取
,用第3节提出的算法求解问题(1),对于不同的N,我们在表2中列出了前4个特征值的数值结果(
为重根)。我们还以
时的数值解作为一个参考解,并在图2中列出了
关于不同的N的误差曲线。

Table 2. For different N, the first four approximate eigenvalue numerical results
表2. 对于不同的N,前4个逼近特征值的数值结果
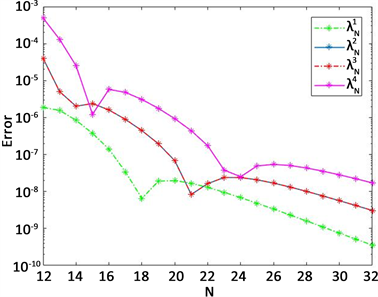
Figure 2. The error between the approximation eigenvalue
and the reference solution
图2. 逼近特征值
与参考解之间的误差
从表2和图2中再次观察到我们的算法是收敛的和高精度的。
5. 结论性注记
本文提出了四阶特征值问题基于降阶格式的一种有效的谱Galerkin逼近。首先,我们建立了原问题的弱形式及其离散格式。其次,我们给出了算法的实现过程。最后通过具体的数值算例来验证算法的有效性和理论结果的正确性。
本文只给出了二维区域
上基于降阶格式的四阶特征值问题的数值试验结果,但文中的方法也可以直接推广到一般的矩形区域以及长方体区域。
本文通过将一个四阶特征值问题转化为一个二阶混合特征值问题,不仅降低了问题的复杂度,还可以结合谱元法应用于一般区域上的四阶特征值问题的计算。