(3 + 1)维幂律3 Zakharov-Kuznetsov方程的行波解——兼论幂律n

Travelling Wave Solutions of a (3 + 1) Dimensional Zakharov-Kuznetsov Equation with Power Law 3—On Power Law n

摘要: 借助于平面动力系统理论，定性分析了非线性(3 + 1)维幂律3 Zakharov-Kuznetsov方程的行波解，同时给出了行波解的分类及近似解计算方法。结合相关文献，整体上讨论了幂律为n时Zakharov-Kuznetsov方程的行波解，由此推广了本文及相应文献中的结果。

Abstract: With the aid of the theory of planar dynamical system, it has qualitatively analysis travelling wave solutions of a nonlinear (3 + 1) dimensional Zakharov-Kuznetsov equation with power law 3. The classification and approximate calculation methods of travelling wave solutions are also derived. Combining corresponding literature, in general, travelling wave solutions the of Zakharov-Kuz- netsov equation with power law n are discussed. Therefore, it extends outcomes in this paper and corresponding literature.

1. 引言

众所周知，(2 + 1)维Zakharov-Kuznetsov方程(ZK方程)

$u_t+\alpha u{u}_x+u_{xxx}+u_{xxy}=0$ (1)

是KdV方程在二维空间的推广形式，它是应用渐进多尺度技术在磁场中发现的一种磁等离子波，在物理学领域有着广泛的应用 [1] ，许多学者对其进行了广泛的研究 [2] - [16] 。一般的，具有幂律 $n$ 非线性(3 + 1)维Zakharov-Kuznetsov方程 [6] [7] [16] 为

$u_t+\alpha u^n{u}_x+{\left(\Delta u\right)}_x=0$ , (2)

其中 $\alpha$ 是非零常数， $\Delta ={\partial }_x^2+{\partial }_y^2+{\partial }_z^2$ 是Laplace算子， $u=u\left(t,x,y,z\right)$ 。受文 [6] [7] [10] [11] [12] [16] 的启发，本文重点考虑幂律3 ZK方程的行波解，整体安排如下。首先，给出相应常微分系统的平衡点情况，如个数和类型；其次，针对行波解的分类及形式进行了讨论，同时给出其近似解的计算方法，基于此，在形式上给出了ZK方程对称的一种表达式；最后，对幂律 $n$ 为正整数时的ZK方程作初步定性分析。

2. 准备工作

对于幂律为3的ZK方程

$u_t+\alpha u^3{u}_x+{\left(\Delta u\right)}_x=0$ ， (3)

作行波变换 $u=u\left(\xi \right)$ ， $\xi =x+y+z-ct$ ， $c\ne 0$ 为波速，积分一次后化为二阶常微分方程(ODE)

$u^{″}=\frac{1}{3}cu-\frac{1}{12}\alpha u^4+C_1$ ， (4)

其中 $C_1$ 是积分常数，上标’(撇)指对 $\xi$ 求导，下同。为简便，设 $x=u$ 和 $y=u^{\prime }$ ，上述ODE化为常微分系统

$x^{\prime }=y,y^{\prime }=\frac{1}{3}cx-\frac{1}{12}\alpha x^4+C_1:=f\left(x\right)$ 。 (5)

显然首次积分为 $H\left(x,y\right):=\frac{1}{3}c{x}^2-\frac{1}{30}\alpha x^5+2C_{1}x-y^2=const.$ ，所定义的轨线为 $\Gamma \left(h\right)=\{\left(x,y\right)|$ $H\left(x,y\right)=h\}$ 。注意，如果设首次积分形式为 $H\left(x,y\right)={\displaystyle \underset{k=0}{\overset{m}{\sum }}{a}_k\left(x\right)y^k}=0$ ， $a_k\left(x\right)$ 为关于 $x$ 的多项式，由交换代数理论的除法定理 [17] [18] 知，存在复数域上多项式 $q\left(x,y\right)=g\left(x\right)+h\left(x\right)y$ ，使得 $\frac{dH}{d\xi }=q\left(x,y\right)H\left(x,y\right)$ ，再取 $m=2$ ，比较系数有 $a_{0}g=$ $a_{1}f$， $a_{1}g+a_{0}h={a^{\prime }}_0+2a_{2}f$ ， $a_{2}g+a_{1}h={a^{\prime }}_1$ ， $a_{2}h={a^{\prime }}_2$ 。计算得 $a_2$ 为非零常数， $a_1=g=h=0$ ，而 $a_0=$ $-2a_2\left(\frac{1}{6}c{x}^2-\frac{1}{60}\alpha x^5+D_{1}x+D_2\right)$ ，又回到上述形式。

当 $C_1=0$ 时，系统(5)的平衡点为 $O=\left(0,0\right)$ 和 $E_{*}=\left(\sqrt[3]{\frac{4c}{\alpha }},0\right)$ 。当 $c>0$ 时， $O$ 为鞍点，由对称原理 [19] 知 $E_{*}$ 为中心；当 $c<0$ 时， $O$ 为中心，而 $E_{*}$ 为鞍点。而轨线经过点 $O$ 和点 $E_{*}$ 时临界值分别为 $h_0=0$ 和 $h_{*}=\frac{4^{\frac{2}{3}}{c}^{\frac{5}{3}}}{5{\alpha }^{\frac{2}{3}}}$ ， $h_{*}$ 与 $c$ 同号。图1给出了 $\alpha ={\alpha }_0$ 时四种轨线图。

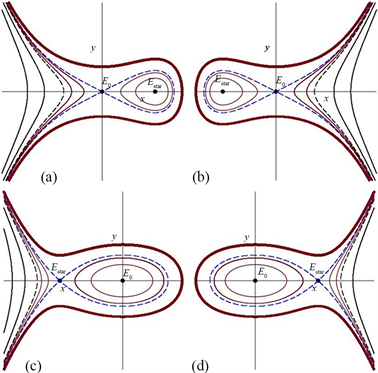
Figure 1. Trajectories with $C_1=0$ : (a) $c,\alpha >0$ ; (b) $c>0,\alpha <0$ ; (c) $c<0,\alpha >0$ ; (d) $c,\alpha <0$

图1. $C_1=0$ 时轨线：(a) $c,\alpha >0$ ；(b) $c>0,\alpha <0$ ；(c) $c<0,\alpha >0$ ；(d) $c,\alpha <0$

3. $C_1\ne 0$ 时的行波解分支

3.1. 平衡点的个数

引入四次方程 $f\left(x\right)=0$ 的判别式 $A_x=-\frac{1}{9}{\alpha }^3{C}_1\ne 0$ ， $B_x=-\frac{1}{324}{\alpha }^4{c}^4<0$ ， $C_x=\frac{1}{729}{\alpha }^6{C}_1^2>0$ ， ${\Delta }_x=\frac{1}{104976}{\alpha }^8\left(64\alpha C_1^3+c^4\right)$ ，分为三种情形进行考虑：情形1. ${\Delta }_x=0$ 或 $\alpha ={\alpha }_0:=-\frac{c^4}{64C_1^3}$ ，此时方程有一对二重实根和一对共轭复根，即仅有一个平衡点；情形2. ${\Delta }_x>0$ 或 $64\alpha C_1^3+c^4>0$ ，此时方程有两个不等实根和一对共轭复根，即有两个平衡点；情形3. ${\Delta }_x<0$ 或 $64\alpha C_1^3+c^4<0$ ，此时方程有两对不等的共轭复根，即没有平衡点。

如果改写方程 $f\left(x\right)=0$ 为 $\frac{1}{3}cx-\frac{1}{12}\alpha x^4=-C_1$ ，则实根情况转化为两个函数 $f_0\left(x\right)=\frac{1}{3}cx-\frac{1}{12}\alpha x^4$ 和直线 $y=-C_1$ 的交点情况。显然，当 $\alpha >0$ ( $\alpha <0$ )时函数 $f_0\left(x\right)$ 有最大(小)值 $f_0\left(\sqrt[\begin{array}{l}3\\ \end{array}]{\frac{c}{\alpha }}\right)=\frac{c}{4}\cdot \sqrt[\begin{array}{l}3\\ \end{array}]{\frac{c}{\alpha }}$ 。以 $\alpha >0$ 为例，当 $f_{\text{0}}\left(\sqrt[\begin{array}{l}3\\ \end{array}]{\frac{c}{\alpha }}\right)<-C_1$ ， $f_0\left(\sqrt[\begin{array}{l}3\\ \end{array}]{\frac{c}{\alpha }}\right)=-C_1$ 和 $f_0\left(\sqrt[\begin{array}{l}3\\ \end{array}]{\frac{c}{\alpha }}\right)>-C_1$ 时，分别对应0个，1个和2个交点，即又回到了上述三种情形。类似的，可以说明 $\alpha <0$ 时的三种情形。图2说明了以上分析。

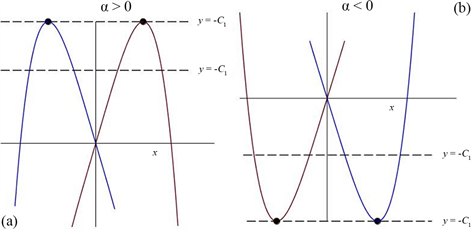
Figure 2. The figures of functions $f_0\left(x\right)$ and $y=-C_1$ : (a) $\alpha >0$ ; (b) $\alpha <0$

图2. 函数 $f_0\left(x\right)$ 与直线 $y=-C_1$ 的图象：(a) $\alpha >0$ ；(b) $\alpha <0$

3.2. 情形1： ${\Delta }_x=0$ 或 $\alpha ={\alpha }_0$

此时唯一的平衡点 $E_{*}=\left(-\frac{4C_1}{c},0\right)$ 为高阶奇点，因Jacobi矩阵 $J\left(E\right)=\left(\begin{array}{cc}0& 1\\ \frac{1}{3}\left(c-\alpha x^3\right)& 0\end{array}\right)$ 的行列式和迹均为零。取变换 $u=x-x_{*}$ ， $v=y$ 和 $u=A{u}_1$ ， $v=A{v}_1$ ， $A=\frac{1}{a_2}$ ， $a_2=\frac{c^2}{8C_1}$ ，化为系统

${u^{\prime }}_1=v_1$ ， ${v^{\prime }}_1=u_1^2-\frac{4}{3c}{u}_1^3+\frac{2}{3c^2}{u}_1^4$ 。 (6)

这等价于系统 $x^{\prime }=y$ ， $y^{\prime }=x^2+o\left({\left|x,y\right|}^4\right)$ ，因此 $E_{*}=\left(-\frac{4C_1}{c},0\right)$ 是余维至少为4的尖点 [20] 。轨线经过该奇点的临界值为 $h_{*}=H\left(x_{*},0\right)=-\frac{16C_1^2}{5c}$ ， $h_{*}$ 与c同号。表1说明了参数间关系，+﹑−分别表示大于﹑小于零(下同)。

Table 1. Relationship of parameters with α = α 0 ( Δ x = 0 )

表1. $\alpha ={\alpha }_0$ ( ${\Delta }_x=0$ )时参数间关系

图3则给出了 $\alpha ={\alpha }_0$ ( ${\Delta }_x=0$ )时的四种轨线图。

3.3. 情形2： ${\Delta }_x>0$

由Sylvester结式知轨线经过平衡点时的临界值h满足方程

$R_{x_{*}}\left(f,f_h\right)=\frac{{\alpha }^3}{1944000}\left[-\frac{125}{16}{\alpha }^2{h}^4+\frac{75}{2}{C}_1{c}^2\alpha h^2+\left(320C_1^{3}c\alpha +c^5\right)h+\left(\frac{3072}{5}{C}_1^5\alpha +3C_1^2{c}^4\right)\right]=0$ ， (7)

Figure 3. Trajectories with $\alpha ={\alpha }_0$ ( ${\Delta }_x=0$ ): (a) $c,C_1>0$ ; (b) $c>0,C_1<0$ ; (c) $c<0,C_1>0$ ; (d) $c,C_1<0$

图3. $\alpha ={\alpha }_0$ ( ${\Delta }_x=0$ )时轨线：(a) $c,C_1>0$ ；(b) $c>0,C_1<0$ ；(c) $c<0,C_1>0$ ；(d) $c,C_1<0$

相应的判别式为 ${\Delta }_h=\frac{{\alpha }^{52}}{M_{\Delta }}{\left(256C_1^3\alpha -c^4\right)}^2{\left(64C_1^3\alpha +c^4\right)}^3\ge 0$ ，其中正数

$M_{\Delta }=632688466200978010631161657879326901519002365853696000000000000$ 。

当 $\alpha ={\alpha }_1:=\frac{c^4}{256C_1^3}$ 时 ${\Delta }_h=0$ ，方程 $R_{x_{*}}\left(f,f_h\right)=0$ 有三个实根，因判别式 $A_h=\frac{c^{76}}{M_A{C}_1^{52}}>0$ ， $B_h=\frac{c^{114}}{M_B{C}_1^{78}}>0$ ， $C_h=\frac{c^{152}}{M_C{C}_1^{104}}>0$ ，其中正数

$M_A=362378034565785000564479090875408362071998718432496278568960000$ ，

$\begin{array}{l}{M}_B=6898311441167723834466142987974349925552300010079724541036061453\\ 456294006942750363090944000000,\end{array}$

$\begin{array}{l}{M}_C=52527135974304507465040925293929299028057843351005699225942573159\\ 6084492213405804540079338670260080650237795941901926400000000.\end{array}$

但一个二重实根 $h_3=-\frac{96C_1^2}{5c}$ 为增根，两个一重实根 $h_1=\frac{32\left(3-2\sqrt{2}\right)C_1^2}{5c}$ 和 $h_2=\frac{32\left(3+2\sqrt{2}\right)C_1^2}{5c}$ 分别对应平衡点 $E_{\alpha }^{\left(1\right)}=\left(\frac{4\left(1-\sqrt{3}\right)C_1}{c},0\right)$ 和 $E_{\alpha }^{\left(2\right)}=\left(\frac{4\left(1+\sqrt{3}\right)C_1}{c},0\right)$ ，相应平衡点处Jacobi矩阵的行列式分别为 $\det J\left(E_{\alpha }^{\left(1\right)}\right)=\frac{1}{2}c\left(1-\sqrt{3}\right)$ 和 $\det J\left(E_{\alpha }^{\left(2\right)}\right)=\frac{1}{2}c\left(1+\sqrt{3}\right)$ 。表2说明了 $\alpha ={\alpha }_1$ 时参数间关系。

Table 2. Relationship of parameters with α = α 1

表2. $\alpha ={\alpha }_1$ 时参数间关系

当 $\alpha \ne {\alpha }_1$ 时 $h_3$ 不存在，方程 $R_{x_{*}}\left(f,f_h\right)=0$ 仅有两个实根。引入变换 $x=\sqrt[\begin{array}{l}3\\ \end{array}]{\frac{c}{\alpha }}z$ ，方程 $f\left(x\right)=0$ 化简为

$f_1\left(z\right)=\frac{1}{3}z-\frac{1}{12}{z}^4+\sqrt[3]{\frac{C_1^3\alpha }{c^4}}=0$ ， (8)

显然 $f_1\left(z\right)=0$ 有两个实根 $z_{*}^{\left(1\right)}<1$ 和 $z_{*}^{\left(2\right)}>1$ ，即有 $x_{*}^{\left(k\right)}=z_{*}^{\left(k\right)}$ ， $k=1,2$ 。由Jacobi矩阵的行列式 $\det J\left(E_{*}^{\left(k\right)}\right)=\frac{1}{3}\alpha \left[{\left(x_{*}^{\left(k\right)}\right)}^3-\frac{c}{\alpha }\right]$ 可知平衡点 $E_{*}^{\left(k\right)}$ 的类型， $k=1,2$ ，另见表3。当然，利用 $f^{\prime }\left(x_{\text{*}}^{\left(k\right)}\right)$ 的符号也可说明。再考虑轨线过平衡点 $E_{*}^{\left(k\right)}$ 时的临界值 $h_k$ ，简记 $x_k=x_{*}^{\left(k\right)}$ 和 $z_k=z_{*}^{\left(k\right)}$ ， $k=1,2$ ，作差有 $h_k-h_l=\frac{c^{\frac{4}{3}}}{{\alpha }^{\frac{1}{3}}}\left(x_k-x_l\right)g\left(z_k,z_l\right)$ ，其中对称函数

$\begin{array}{l}g\left({\lambda }_1,{\lambda }_2\right)=\frac{-1}{30}\left({\lambda }_1^3{\lambda }_2+{\lambda }_1^2{\lambda }_2^2+{\lambda }_1{\lambda }_2^3\right)+\frac{1}{20}\left({\lambda }_1^4+{\lambda }_2^4\right)=\frac{1}{60}{\left({\lambda }_1-{\lambda }_2\right)}^2\left[{\left({\lambda }_1+{\lambda }_2\right)}^2+2{\left({\lambda }_1+\frac{1}{2}{\lambda }_2\right)}^2+\frac{3}{2}{\lambda }_2^2\right]\\ >0,{\lambda }_1<1,{\lambda }_2>1,\end{array}$

可得 $h_1$ 和 $h_2$ 的大小关系，见表3 (同表2)。图4给出了 ${\Delta }_x>0$ 时四种轨线图。

Table 3. Relationship of parameters with Δ x > 0 and α ≠ α 1

表3. ${\Delta }_x>0$ 且 $\alpha \ne {\alpha }_1$ 时参数关系

3.4. 情形3： ${\Delta }_x<0$

显然 $\alpha C_1<0$ 。当 $\alpha >0$ (或 $\alpha <0$ )时轨线开口向左(或右)，每支轨线的定义区间为 $\left(-\infty ,x_h\right)$ (或 $\left(x_h,+\infty \right)$ )，且唯一的 $x_h$ 随h增大而增大(或减小)，而行波解是无界的。图5给出了 ${\Delta }_x<0$ 时两种轨线图。

Figure 4. Trajectories with ${\Delta }_x>0$ : (a) $c,C_1>0$ ; (b) $c>0,C_1<0$ ; (c) $c<0,C_1>0$ ; (d) $c,C_1<0$

图4. ${\Delta }_x>0$ 时轨线图：(a) $c,C_1>0$ ；(b) $c>0,C_1<0$ ；(c) $c<0,C_1>0$ ；(d) $c,C_1<0$

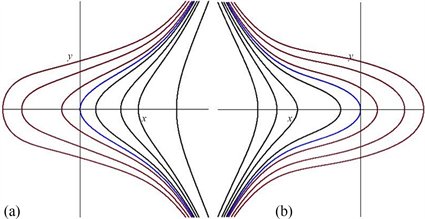
Figure 5. Trajectories with ${\Delta }_x<0$ : (a) $\alpha <0$ ; (b) $\alpha >0$

图5. ${\Delta }_x<0$ 时轨线：(a) $\alpha <0$ ；(b) $\alpha >0$

4. 行波解和对称

4.1. 行波解的分类及形式

为方便讨论行波解的形式，取变换 $x=\frac{w}{\lambda }$ ， $\lambda =-\sqrt[\begin{array}{l}3\\ \end{array}]{\frac{\alpha }{30}}$ ，由 $H\left(x,y\right)=h$ 可得标准形式

$\pm \left(\xi -{\xi }_0\right)={\displaystyle {\int }_{}^w\frac{\text{d}z}{\sqrt{F\left(z\right)}}}$ ， $F\left(w\right)=w^5+\frac{1}{3}{w}^2+2C_1\lambda w-{\lambda }^{2}h$ ， (9)

其中 ${\xi }_0$ 是积分常数。根据五阶多项式完全判别系统法 [21] ，引入判别式

$D_2=0$ ， $D_3=-5c^2$ ， $D_4=-\frac{1}{3}{c}^4-\frac{20}{3}c{C}_1\alpha h-\frac{128}{3}{C}_1^3\alpha$ ，

$D_5=-\frac{1}{5400}\left(49152C_1^2\alpha +25600C_1^3\alpha ch+240C_1^2{c}^4+3000C_1\alpha c^2{h}^2-625{\alpha }^2{h}^4+80c^{5}h\right)\cdot \sqrt[3]{30{\alpha }^2}$ ，

$E_2=\frac{5}{6}{c}^2\left(16C_1^2+5ch\right)\cdot \sqrt[3]{30{\alpha }^2}$ ， $F_2=\frac{1}{3}{c}^2$ ，

可对行波解作分类并形式上给出解。

情形1： $D_5=D_4=0$ ， $D_3<0$ ， $E_2\ne 0$ 。

这种情形存在，例如取 $h=-\frac{96C_1^2}{5c}$ ， $\alpha =\frac{c^4}{256C_1^3}$ 。此时 $F\left(w\right)=\left(w-a\right){\left(w^2+rw+s\right)}^2$ ，其中 $a=-\frac{2}{15}\cdot \sqrt[3]{225c}$ ， $r=-\frac{1}{15}\cdot \sqrt[3]{225c}$ ， $s=\frac{1}{150}{\left(225c\right)}^{\frac{2}{3}}$ 。当 $w>a$ 时行波解的形式为

$\pm \left(\xi -{\xi }_0\right)=-\frac{2}{\rho \sqrt{4s-r^2}}\left(\cos \phi \cdot \arctan \frac{2\rho \sin \phi \sqrt{w-a}}{w-a-{\rho }^2}+\frac{\sin \phi }{2}\cdot \ln \frac{w-a-{\rho }^2-2\rho \cos \phi \sqrt{w-a}}{w-a-{\rho }^2+2\rho \cos \phi \sqrt{w-a}}\right)$ ，(10)

其中 $\rho ={\left(a^2+ra+s\right)}^{\frac{1}{4}}$ ， $\phi =\frac{1}{2}\arctan \frac{\sqrt{4s-r^2}}{-2a-r}$ 。

情形2： $D_5=D_4=E_2=0$ ， $D_3<0$ 。

此即为 ${\Delta }_x=0$ 或 $\alpha ={\alpha }_0$ 的情形，且 $F\left(w\right)={\left(w-a\right)}^3\left[{\left(w-l_1\right)}^2+s_1^2\right]$ ，其中 $a=-\sqrt[\begin{array}{l}3\\ \end{array}]{\frac{c}{30}}$ ， $l_1=\frac{1}{20}\cdot \sqrt[3]{{30}^{2}c}$ ， $s_1=\pm \frac{\sqrt{2}}{4}\cdot \sqrt[3]{\sqrt{30}c}$ 。当 $w>a$ 时，行波解的形式为

$\begin{array}{l}\pm \left(\xi -{\xi }_0\right)=-\frac{\tan \theta +\cot \theta }{2\left(s_1\tan \theta -l_1-a\right)\sqrt{\frac{s_1}{{\sin }^{3}2\theta }}}F\left(\phi ,k\right)-\frac{s_1\left(\tan \theta +\cot \theta \right)}{s_1\cot \theta +l_1+a}\\ \times \left[\frac{\tan \theta +l_1+a}{\left(s_1\cot \theta +l_1-a\right)\sin \phi }\sqrt{1-k^2{\sin }^2\phi }+F\left(\phi ,k\right)-E\left(\phi ,k\right)\right],\end{array}$ (11)

其中 $\tan 2\theta =\frac{s_1}{a-l_1}$ ， $k=\sin \theta$ ， $0<\theta <\frac{\pi }{2}$ ，辅助函数 $F\left(\phi ,k\right)={\displaystyle {\int }_0^{\phi }\frac{\text{d}\psi }{\sqrt{1-k^2{\sin }^2\psi }}}$ ， $E\left(\phi ,k\right)={\displaystyle {\int }_0^{\phi }\sqrt{1-k^2{\sin }^2\psi }\text{d}\psi }$ 。

情形3： $D_5=0$ ， $D_4<0$ 。

这种情形存在，例如取 $h=0$ ， $\alpha =-\frac{5c^4}{1024C_1^3}$ 。此时 $F\left(w\right)=\left(w-a\right)\left(w-\beta \right)\left[{\left(w-l_1\right)}^2+s_1^2\right]$ ，a， $\beta$ ， $l_1$ 及 $s_1$ 是实数。当 $w>\beta$ 时，如果 $a\ne l_1-s_1\tan \theta$ 且 $a\ne l_1+s_1\tan \theta$ ，则行波解的形式为

$\begin{array}{l}\pm \left(\xi -{\xi }_0\right)=-\frac{\tan \theta +\cot \theta }{2\left(s_1\tan \theta -l_1-a\right)\sqrt{\frac{s_1}{{\sin }^{3}2\theta }}}F\left(\phi ,k\right)-\frac{s_1\left(\tan \theta +\cot \theta \right)}{s_1\cot \theta +l_1+a}\\ \times \left[\frac{\tan \theta +l_1+a}{\left(s_1\cot \theta +l_1-a\right)\sin \phi }\sqrt{1-k^2{\sin }^2\phi }+F\left(\phi ,k\right)-E\left(\phi ,k\right)\right]\end{array}$ ； (12a)

如果 $a=l_1-s_1\tan \theta$ ，则行波解的形式为

$\pm \left(\xi -{\xi }_0\right)=\sqrt{\frac{{\sin }^{3}2\theta }{4s^3}}\left[\frac{1}{k}\arcsin \left(k\sin \phi \right)-F\left(\phi ,k\right)\right]$ ； (12b)

如果 $a=l_1+s_1\tan \theta$ ，则行波解的形式为

$\pm \left(\xi -{\xi }_0\right)=\sqrt{\frac{{\sin }^{3}2\theta }{4s^3}}\left[F\left(\phi ,k\right)-\frac{1}{\sqrt{1-k^2}}\ln \frac{\sqrt{1-k^2{\sin }^2\phi }+\sqrt{1-k^2}\sin \phi }{\cos \phi }\right]$ 。 (12c)

其中 $\tan 2\theta =\frac{s_1}{\beta -l_1}$ ， $k=\sin \theta$ ， $0<\theta <\frac{\pi }{2}$ 。

情形4： $D_5<0$ 。

这种情形存在，例如取 $h=0$ ， $\alpha =\frac{C_1^3}{c^4}$ 。此时 $F\left(w\right)=\left(w-a_1\right)\left(w-a_2\right)\left(w-a_3\right)\left[{\left(w-l_1\right)}^2+s_1^2\right]$ ，其中 $a_1$ ， $a_2$ ， $a_3$ ， $l_1$ 及 $s_1$ 是实数，行波解的形式为

$\pm \left(\xi -{\xi }_0\right)={\displaystyle {\int }_{}^w\frac{\text{d}z}{\sqrt{\left(z-a_1\right)\left(z-a_2\right)\left(z-a_3\right)\left[{\left(z-l_1\right)}^2+s_1^2\right]}}}$ 。 (13)

情形5： $D_5>0$ ， $D_3<0$ ， $D_2=0$ 。

这种情形存在，例如取 $h=0$ ， $\alpha =-\frac{c^4}{C_1^3}$ 。此时 $F\left(w\right)=\left(w-a\right)\left[{\left(w-l_1\right)}^2+s_1^2\right]\left[{\left(w-l_2\right)}^2+s_2^2\right]$ ，a， $l_1$ ， $s_1$ ， $l_2$ 及 $s_2$ 是实数，行波解的形式为

$\pm \left(\xi -{\xi }_0\right)={\displaystyle {\int }_{}^w\frac{\text{d}z}{\sqrt{\left(z-a\right)\left[{\left(z-l_1\right)}^2+s_1^2\right]\left[{\left(z-l_2\right)}^2+s_2^2\right]}}}$ 。 (14)

注意， $D_5=0$ 且 $D_4>0$ 的情形不存在，因要求 $h\ne 0$ ，否则 $h=0$ 时退化为情形3。当 $C_1=0$ 时，仅有情形3﹑情形4和情形5成立，因 $D_4=-\frac{1}{3}{c}^4<0$ 。总之，行波解的形式由上述五类情形所规定。

4.2. 对称

引入变换 $u\to u+\epsilon \sigma$ ， $\epsilon$ 充分小，原方程的对称 $\sigma$ 应满足方程

${\frac{\partial }{\partial \epsilon }\hat{K}\left(u+\epsilon \sigma \right)|}_{\epsilon =0}={\sigma }_t+\alpha {\left(u^3\sigma +\Delta \sigma \right)}_x=0$ ， (15)

其中算子 $\hat{K}$ 定义为 $\hat{K}\left(u\right)=u_t+\alpha u^3{u}_x+{\left(\Delta u\right)}_x$ 。同上，考虑行波解 $\sigma =\sigma \left(\xi \right)$ ，并引入mapping and deformation关系 [22] $\sigma =\Sigma \left(u\right)$ ，方程(15)可化为三阶ODE

$F\left(u\right)\frac{{\text{d}}^3\Sigma \left(u\right)}{\text{d}{u}^3}+3f\left(u\right)\frac{{\text{d}}^2\Sigma \left(u\right)}{\text{d}{u}^2}+\alpha u^2\Sigma \left(u\right)=0$ , (16)

其中辅助函数 $F\left(u\right)=H\left(u,0\right)-h=\frac{1}{3}cu-\frac{\alpha }{30}{u}^5+2C_{1}u-h$ 。上述常微分方程的通解形式为

$\sigma \left(u\right)=\sqrt{F\left(u\right)}\left\{R_1+{\displaystyle {\int }_{}^u\frac{R_{2}z+R_3}{F^{{}^{\frac{3}{2}}}\left(z\right)}\text{d}z}\right\}$ ， (17)

其中 $R_1$ ﹑ $R_2$ 和 $R_3$ 是积分常数，而u是原方程(4)的行波解。因此有了以上行波解的分类工作，理论上是可以得到相应的对称 $\sigma$ 。

4.3. 近似解

Runge-Kutta法可以给出解的数值结果，但无法给出解的表达式；尽管同伦微扰法(HPM) [23] 和Adomian分解法(ADM) [24] [25] [26] [27] 可以给出近似解的幂级数表达式，对于结点情形尚可以采用，但收敛速度较慢，特别是在周期解情形，而一个物理系统中又常常考虑有界的行波解。给定初值 $x\left(\xi \right)=x_0$ ， $y\left(\xi \right)=y_0$ ，对于系统(5)，按文 [28] ，由HPM和ADM给出的前五阶近似解为

$\begin{array}{l}x\left(\xi \right)\approx x_0+y_0\xi +\frac{1}{24}\left(-\alpha x_0^4+4c{x}_0+12C_1\right){\xi }^2+\frac{1}{18}{y}_0\left(-\alpha x_0^3+c\right){\xi }^3\\ +\frac{1}{4320}\left(5{\alpha }^2{x}_0^7-25\alpha c{x}_0^7-60C_1\alpha x_0^3-180\alpha x_0^2{y}_0^2+20c^2{x}_0+60C_{1}c\right){\xi }^4\\ +\frac{1}{1080}\left(\frac{13}{4}{\alpha }^2{x}_0^2-11\alpha c{x}_0^3-27C_1\alpha x_0^2-18\alpha x_0{y}_0^2+c^2\right){\xi }^5,\end{array}$ (18a)

$\begin{array}{l}y\left(\xi \right)\approx y_0+\frac{1}{12}\left(-\alpha x_0^4+4c{x}_0+12C_1\right)\xi +\frac{1}{6}\left(-\alpha x_0^3+c\right)y_0{\xi }^2\\ +\frac{1}{216}\left({\alpha }^2{x}_0^7-5\alpha c{x}_0^4-12C_1\alpha x_0^3-36\alpha x_0^2{y}_0^2+4c^2{x}_0+12C_{1}c\right){\xi }^3\\ +\frac{1}{216}\left(\frac{13}{4}{\alpha }^2{x}_0^6-11\alpha c{x}_0^3-27C_1\alpha x_0^2-18\alpha x_0{y}_0^2+c^2\right)y_0{\xi }^4\\ +\frac{1}{51840}[-13{\alpha }^3{x}_0^{10}+96{\alpha }^{2}c{x}_0^7+264{\alpha }^{2}c{x}_0^6+1152{\alpha }^2{x}_0^5{y}_0^2\\ +-180\alpha c^2{x}_0^4-960\alpha c{C}_1{x}_0^3-2448\alpha \left(c{y}_0^2+\frac{9}{17}{C}_1^2\right)x_0^2]\\ +\left(-5184C_1\alpha y_0^2+16c^3\right)x_0-864\alpha y_0^4+48C_1{c}^2]{\xi }^5.\end{array}$ (18b)

当然，也可用幂级数展开法得到上述结果。以 ${\Delta }_x>0$ ， $c=\alpha =C_1=1$ ， $x_0=y_0=0.1$ 为例，图6将这两种方法所得近似解与Runge-Kutta 45法进行比较，结果表明当 $\xi$ 比较小时，近似可以接受。

Figure 6. Approximate solutions via HPM (black solid line), ADM (black dot line) and Runge-Kutta 45 method (red solid line): (a) $x\left(\xi \right)$ ; (b) $y(\; \xi \; )$

图6. 同伦微扰法(黑色实线)﹑Adomian分解法(黑色点线)与Runge-Kutta 45法(红色实线)所得近似解：(a) $x\left(\xi \right)$ ；(b) $y(\; \xi \; )$

鉴于行波解的表达式如此复杂，以及ADM和HPM的局限性，参照文 [29] [30] ，这里给出相应多模态近似解的计算方法。仍以上述 $c=\alpha =C_1=1$ 为例，取多模态近似解 $x\left(t\right)=a_0+a_1\cos \left(2wt\right)+a_2\cos \left(4wt\right)$ ，其中w为频率， $f=\frac{1}{w}$ 。与文 [16] [29] [30] 不同，在一个周期 $T=\frac{2\pi }{w}$ 上对Hamilton函数 $H\left(x,y\right)$ 积分有 $\bar{H}={\displaystyle {\int }_0^{T}H\left(x,y\right)\text{d}t}=0$ ，即可得耦合代数方程组

$\frac{\partial }{\partial a_0}\bar{H}:8a_0^2+24a_0^2{a}_1^2+24a_0^2{a}_2^2+24a_0{a}_1^2{a}_2+3a_1^4+12a_1^2{a}_2^2+3a_2^4-32a_0-96=0$ ， (19a)

$\frac{\partial }{\partial a_1}\bar{H}:-12+\left[\frac{3}{8}{a}_2^2+\frac{3}{2}{a}_0{a}_2^2+\left(\frac{3}{2}{a}_0^2+\frac{1}{2}{a}_1^2\right)a_2+a_0^3+\frac{3}{4}{a}_0{a}_1^2-1\right]f^2=0$ ， (19b)

$\frac{\partial }{\partial a_2}\bar{H}:\left[\frac{3}{4}{a}_0{a}_2^2+\frac{9}{16}{a}_1^2{a}_2^2+\left(a_0^3+\frac{3}{2}{a}_0{a}_1^2-1\right)a_2+\frac{3}{4}{a}_0^2{a}_1^2+\frac{1}{8}{a}_1^4\right]f^2-48a_2=0$ 。 (19c)

结合初始条件 $x\left(0\right)=1$ 有解 $f\approx 1.358874058$ ， $a_0\approx 1.795811040$ ， $a_1\approx -0.9048387263$ 及 $a_2\approx 0.1090276862$ 。图7(a)刻画了近似解(黑色实线)与实际解(红色点线)的近似程度，在前几个周期内两者非常吻合；图7(b)刻画了所得近似轨线(黑线)与实际周期轨(红线)之间的近似程度，近似程度很好。总之，这是一种有效的近似求解方法。类似的，理论上可以作出其它情形下的近似周期解。

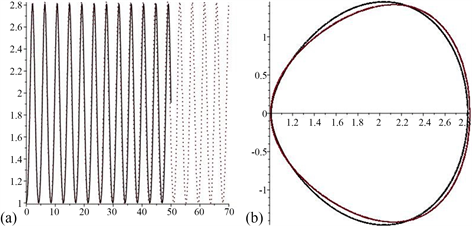
Figure 7. (a) Multimode approximate solution (black solid line); (b) periodic trajectory via multimode approximate solution (black line)

图7. (a) 多模态近似解(黑色实线)；(b) 由多模态近似解所得周期轨(黑线)

5. 幂律n ZK方程的行波解

结合前几节的结果，类似于 $C_1=0$ 时数形结合法对平衡点个数的讨论，本节研究幂律n ZK方程(2)及行波解对应的系统

$x^{\prime }=y$ ， $y^{\prime }=\frac{1}{3}cx-\frac{\alpha }{3\left(n+1\right)}{x}^{n+1}+C_1:=f\left(x\right)$ 。 (20)

首先考虑n为奇数情形。当 ${\Delta }_n:={\alpha }^{n+1}\left\{\alpha C_1^n+{\left[\frac{n}{3\left(n+1\right)}\right]}^n{c}^{n+1}\right\}>0$ 时，有2个平衡点 $E_{\text{*}}^{\left(k\right)}=\left(x_{\text{*}}^{\left(k\right)},0\right)$ ， $x_{*}^{\left(1\right)}<x_n$ ， $x_{*}^{\left(2\right)}>x_n$ 。结合 $f^{\prime }\left(x_{*}^{\left(k\right)}\right)$ 的符号知：若 $\alpha >0$ ，则 $E_{\text{*}}^{\left(1\right)}$ 是鞍点， $E_{\text{*}}^{\left(2\right)}$ 是中心；若 $\alpha <0$ ，则 $E_{*}^{\left(1\right)}$ 是中心， $E_{\text{*}}^{\left(2\right)}$ 是鞍点。当 ${\Delta }_n=0$ 时，只有1个高阶奇点 $E_{*}=\left(\sqrt[\begin{array}{l}n\\ \end{array}]{\frac{c}{\alpha }},0\right)$ ，因 $\det J\left(E_{*}\right)=0$ ，同样是余维至少为4的尖点。当 ${\Delta }_n<0$ 时，没有平衡点。这样，平衡点可有0个﹑1个或2个。

再考虑n为偶数情形。同上，如果 $\alpha c<0$ ，则仅有一个平衡点，因 ${f^{\prime }}_0\left(x\right)$ 的单调性。如果 $\alpha c>0$ ，则：当 ${\Delta }_n={\alpha }^{n+1}\left\{\alpha C_1^n-{\left[\frac{n}{3\left(n+1\right)}\right]}^n{c}^{n+1}\right\}<0$ 时，平衡点有3个；当 ${\Delta }_n=0$ 时，平衡点有2个；当 ${\Delta }_n>0$ 时，平衡点仅有1个。注意， $\alpha c<0$ 的情形包含在 ${\Delta }_n>0$ 的情形中。显然，可结合 $f^{\prime }\left(x_{*}^{\left(k\right)}\right)$ 的符号得到平衡点的类型(鞍点﹑中心或尖点)，总结如下，与文 [16] 一致。

当 ${\Delta }_n>0$ 时，若 $\alpha >0$ ，则唯一的平衡点 $E_{*}$ 是中心；反之， $\alpha <0$ 时 $E_{*}$ 是鞍点。

当 ${\Delta }_n<0$ 时，设三个平衡点为 $E_{*}^{\left(k\right)}$ ， $k=1,2,3$ ， $x_{*}^{\left(1\right)}<x_{*}^{\left(2\right)}<x_{*}^{\left(3\right)}$ 。若 $\alpha >0$ ( $\alpha$ ﹑c同号)，则 $E_{*}^{\left(1\right)}$ ﹑ $E_{*}^{\left(3\right)}$ 是中心，而 $E_{*}^{\left(2\right)}$ 是鞍点；若 $\alpha <0$ ，则 $E_{*}^{\left(1\right)}$ ﹑ $E_{*}^{\left(3\right)}$ 是鞍点，而 $E_{*}^{\left(2\right)}$ 是中心。

当 ${\Delta }_n=0$ 时，设双曲平衡点为 $E_{*}^H$ ，退化平衡点为 $E_{*}^D=\left(x_n^{\left(k\right)},0\right)$ ， $k=1$ 或2， $x_n^{\left(1\right)}=-\sqrt[\begin{array}{l}n\\ \end{array}]{\frac{c}{\alpha }}$ ， $x_n^{\left(2\right)}=\sqrt[\begin{array}{l}n\\ \end{array}]{\frac{c}{\alpha }}$ ，同上 $E_{*}^D$ 是余维至少为4的尖点；而 $\alpha >0$ ( $\alpha$ ﹑c同号)时 $E_{*}^H$ 是中心，反之， $\alpha <0$ 时 $E_{*}^H$ 是鞍点。

总之，平衡点可有1个﹑2个或3个。图8描述了 $n=2$ 时利用数形结合法对平衡点个数的分析。

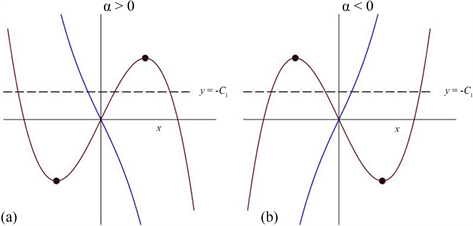
Figure 8. Analysis of number of equilibria with $n=2$ : (a) $\alpha >0$ ; (b) $\alpha <0$

图8. $n=2$ 时平衡点个数分析：(a) $\alpha >0$ ；(b) $\alpha <0$

此外，可以得到首次积分 $H\left(x,y\right)=\frac{1}{3}c{x}^2-\frac{2\alpha }{3\left(n+1\right)\left(n+2\right)}{x}^{n+2}+2C_{1}x-y^2=const.$ ，当然，理论上也可使用除法定理获得，例如 $n=4$ 时取 $m=2$ ， $H={\displaystyle \underset{k=0}{\overset{m}{\sum }}{a}_k\left(x\right)y^k}$ 有 $H=\frac{1}{45}{a}_2\left(\alpha x^6-15c{x}^2-90C_{1}x+45y^2\right)+A_0$ ，其中 $a_2$ 和 $A_0$ 均为待定常数。这样，轨线经过平衡点 $E\left(x_{*},0\right)$ 时临界值h由方程组 $f\left(x_{*}\right)=0$ ， $f_h\left(x_{*}\right)=H\left(x_{*},0\right)-h=0$ 决定，即临界值满足( $n+1$ )次代数方程

$\begin{array}{c}{R}_{x_{*}}\left(f,f_h\right)=\left|\begin{array}{ccccccccc}\frac{-\alpha }{3\left(n+1\right)}& 0& & \cdots & \frac{c}{3}& C_1& & \cdots & 0\\ 0& \frac{-\alpha }{3\left(n+1\right)}& & \cdots & & \ddots & \ddots & & ⋮\\ ⋮& ⋮& & ⋮& & & & & \\ 0& 0& & \cdots & & \cdots & & \frac{c}{3}& C_1\\ \frac{-2\alpha }{3\left(n+1\right)\left(n+2\right)}& 0& & \cdots & 2C_1& -h& & \cdots & 0\\ 0& \frac{-2\alpha }{3\left(n+1\right)\left(n+2\right)}& & \cdots & & \ddots & \ddots & & ⋮\\ 0& 0& & \cdots & & & & & \\ ⋮& ⋮& & ⋮& & & & -h& 0\\ 0& 0& & \cdots & & \cdots & & 2C_1& -h\end{array}\right|\\ =a_{n+1}{h}^{n+1}+\cdots +a_{1}h+a_0=0,\end{array}$ (21)

其中 $a_{n+1}=-{\left(\frac{\alpha }{3\left(n+1\right)}\right)}^{n+2}$ ， $a_0=R_{x_{*}}\left(f,{f_h|}_{h=0}\right)$ ，而行列式是 $2n+3$ 阶的。再结合高阶多项式完全判别系统法，理论上可说明h的实根情况及相应轨线的拓扑结构。同时，方程 $R_{x_{*}}\left(f,f_h\right)=0$ 的实根个数不少于方程 $f\left(x\right)=0$ 的实根个数，这也启发我们思考如下结论：

对于连续函数 $f\left(x,y\right)$ 和 $g\left(x,y\right)$ ，若连续的轨线族 $H\left(x,y\right)=h$ 由微分方程 $\frac{\text{d}x}{f\left(x,y\right)}=\frac{\text{d}y}{g\left(x,y\right)}$ 给出，h为实数，关于参数h的方程 $\phi \left(h\right)=0$ 由方程组 $f\left(x,y\right)=g\left(x,y\right)=H\left(x,y\right)-h=0$ 所确定，则方程 $\phi \left(h\right)=0$ 的实根个数(重根按单重根计算)不少于方程 $f\left(x,y\right)=g\left(x,y\right)=0$ 的实根个数？除去 $\phi \left(h\right)=0$ 的增根，两者的“剩余”实根个数是否相等(存在“剩余”实根间的一一映射)？

例如，对于实数域上的多项式 $f\left(x\right)={\displaystyle \underset{k=0}{\overset{n}{\sum }}{a}_k{x}^k}$ 和 $f_h\left(x\right)={\displaystyle \underset{k=0}{\overset{n}{\sum }}\frac{a_k}{k+1}{x}^{k+1}}-h$ ， $a_n\ne 0$ ，n为正整数，h为实数，则需要考虑“结式方程” $R_x\left(f,f_h\right)=0$ 和方程 $f\left(x\right)=0$ 的实根情况。

因此，在给定参数条件下，可获得相图分支及光滑孤立波解、周期波解的存在性定理，详述如下。

定理1：当n为奇数， ${\Delta }_n>0$ ， $\alpha >0$ (或 $\alpha <0$ )时，对应系统(20)连接鞍点 $E_{\text{*}}^{\left(1\right)}$ (或 $E_{\text{*}}^{\left(2\right)}$ )的同宿轨道 $H\left(x,y\right)=h_1$ (或 $H\left(x,y\right)=h_2$ )，方程(2)有一个光滑孤立波解；对应系统(20)的周期轨道 $H\left(x,y\right)=h$ ，h位于 $h_1$ 和 $h_2$ 之间，方程(2)有一族周期波解。

定理2：当n为偶数， ${\Delta }_n<0$ ， $\alpha <0$ 时，对应系统(20)连接鞍点 $E_{\text{*}}^{\left(1\right)}$ 和 $E_{*}^{\left(3\right)}$ 的异宿轨道 $H\left(x,y\right)=h$ ，方程(2)有一个扭(反扭)波解；对应系统(20)的周期轨道 $H\left(x,y\right)=h$ ，h位于 $h_1$ (或 $h_3$ )和 $h_2$ 之间，方程(2)有一族周期波解。

定理3：当n为偶数， ${\Delta }_n<0$ ， $\alpha >0$ 时，对应系统(20)连接鞍点 $E_{\text{*}}^{\left(2\right)}$ 的同宿轨道 $H\left(x,y\right)=h_2$ ，方程(2)有两个光滑孤立波解；对应系统(20)环绕平衡点 $E_{\text{*}}^{\left(1\right)}$ ﹑ $E_{\text{*}}^{\left(2\right)}$ 和 $E_{*}^{\left(3\right)}$ 的大范围周期轨道 $H\left(x,y\right)=h$ ， $h\ne h_2$ ，方程(2)有一族周期波解；对应系统(20)分别环绕中心 $E_{\text{*}}^{\left(1\right)}$ 和 $E_{*}^{\left(3\right)}$ 的两族周期轨道 $H\left(x,y\right)=h$ ，h分别位于 $h_1$ 和 $h_2$ 及 $h_2$ 和 $h_3$ 之间，方程(2)有两族周期波解。

定理4：当n为偶数， ${\Delta }_n>0$ ， $\alpha >0$ 时，对应系统(20)的周期轨道 $H\left(x,y\right)=h$ ， $h\ne h_{*}$ ，方程(2)有一族周期波解。

最后，原方程(2)的对称 $\sigma$ 应满足方程

${\frac{\partial }{\partial \epsilon }\hat{K}\left(u+\epsilon \sigma \right)|}_{\epsilon =0}={\sigma }_t+\alpha {\left(u^n\sigma +\Delta \sigma \right)}_x=0$ ， (22)

类似的，引入关系 $\sigma =\Sigma \left(u\right)$ 后，其一般的表达式同(17)，但 $F\left(u\right)=H\left(u,0\right)-h=\frac{1}{3}cu-\frac{2\alpha }{3\left(n+1\right)\left(n+2\right)}{u}^{n+2}+2C_{1}u-h$ ，而u是原方程(2)的行波解。

6. 总结与讨论

文 [16] 的工作隐含了特征为0的实数域R上椭圆曲线 $y^2=a{x}^3+b{x}^2+cx+d$ 的若干思考。结合文 [6] [7] [16] ，本文整体上定性分析了幂律n ( $n\ge 2$ 且为正整数)ZK方程行波解及其性质，对于其它非线性偏微分方程的研究具有一定参考意义，如(2 + 1)维广义Zakharov-Kuznetsovmodifiedequal-width (ZK-MEW)方程 [31]

$u_t+a{\left(u^n\right)}_x+{\left(b{u}_{xt}+c{u}_{yy}\right)}_x=0$ 。

致谢

感谢编辑和审稿人的工作，感谢温州大学赵敏老师和戴传军老师，感谢乐清市柳市镇第三中学郑孟老师和赵淑静老师，感谢乐清市城南中学陈谱锦老师。

参考文献