基于各向异性扩散PDE的曲面重建

Surface Reconstruction Based on Anisotropic Diffusion Paritial Differential Equation

摘要: Possion方程是曲面重建中能够保持曲面平滑的简单有效方法之一，由于该方程是各向同性扩散的，因此不可避免会平滑曲面尖锐特征。本研究通过选取合适的高斯核与结构张量进行卷积构造能够保留曲面细节的扩散张量，在Possion方程中引入该扩散张量为梯度设置各向异性的权重，从而建立能够兼顾曲面平滑和尖锐特征的基于各向异性扩散PDE重建模型；使用Guass消元法求解离散后的模型得到高度值。数值实验结果表明，本研究方法能够保持物体的尖锐及边缘特征，重建效果更佳。

Abstract: Possion equation is one of the simple and effective methods to keep the surface smooth in surface reconstruction. Since the equation is isotropic diffusion, it will inevitably smooth the sharp features of the surface. In this study, the diffusion tensor that can retain the details of the surface was con-structed by convolution of Gaussian kernel and structure tensor, and the diffusion tensor was in-troduced into Possion equation to set the weight of anisotropy for gradient, so as to establish a re-construction model based on anisotropic diffusion paritial differential equation that can give con-sideration to both smooth and sharp features of the surface. Guass elimination method was used to solve the discrete model to get the height value. Numerical experimental results show that the proposed method can preserve the sharp and edge features of the object, and the reconstruction effect is better.

1. 引言

三维曲面重建中由光度立体(PS)和明暗恢复形状(SfS) [1] 、偏振恢复形状(SfP) [2] 获取的梯度场容易受到噪声和异常值的干扰，Frankot [3] 基于各向同性扩散的误差泛函，使用傅里叶基函数将不可积梯度场投影到一个可积集中估计曲面高度，重建速度快，但对异常值的鲁棒性较差。Simchony [4] 通过直接求各向同性扩散的Possion方程的解析解，其恢复的曲面高度可以有效克服噪声和异常值，但同时也会平滑曲面中尖锐的特征。为了保留更多的曲面细节，Agrawal [5] 和Queau [6] 在梯度积分获取曲面高度的过程中，基于控制梯度权重的各向异性来重建曲面，该方法既光滑了曲面又保留了边缘特征，但对具有尖锐特征物体的重建效果不佳。因此，在前人方法的基础上，本研究构造了一个保尖锐的扩散张量，根据扩散系数在梯度积分过程中为梯度设置了空间变化的各向异性权重来重建曲面，在克服噪声干扰的同时保持曲面边缘及尖锐的特征。

2. 基于各向异性扩散PDE曲面重建模型

考虑 $M\times N$ 矩形网格的图像，记 $\left\{p\left(x,y\right),q\left(x,y\right)\right\}$ 表示在这个网格上给定的不可积梯度场。给定 $\left\{p,q\right\}$ ，目的是获取曲面高度Z。记 $\left\{Z_x,Z_y\right\}$ 表示Z的梯度场，为了使测量的梯度场更接近估计的梯度场，本研究根据Agrawal [5] 提出的偏微分方程(Paritial Differential Equation, PDE)：

$\nabla \left(f_1\left(Z_x,Z_y\right),f_2\left(Z_x,Z_y\right)\right)-\frac{\partial E}{\partial Z}=\nabla \left(f_3\left(p,q\right),f_4\left(p,q\right)\right)$ (1)

在该方程的基础上，引用了魏克特 [7] 提出的一种基于散度的图像恢复方程 $I_t=\nabla \left(D\nabla I\right)$ 。其中， $D$ 是一个的 $2\times 2$ 对称正定矩阵，称为扩散张量，在每个像素点，扩散张量 $D$ 可以写成

$D\left(x,y\right)=\left[\begin{array}{cc}{d}_{11}\left(x,y\right)& d_{21}\left(x,y\right)\\ d_{12}\left(x,y\right)& d_{22}\left(x,y\right)\end{array}\right]$ 。在方程(1)式中引入扩散张量 $D$ 修改 $f_i$ 得到了一个基于各向异性扩散

PDE曲面重建模型，如下：

$\nabla \left(d_{11}{Z}_x+d_{21}{Z}_y,d_{12}{Z}_x+d_{22}{Z}_y\right)=\nabla \left(d_{11}p+d_{21}q,d_{12}p+d_{22}q\right)$ (2)

也可以写成

$\nabla \left(D\left[\begin{array}{c}{Z}_x\\ Z_y\end{array}\right]\right)=\nabla \left(D\left[\begin{array}{c}p\\ q\end{array}\right]\right)$ (3)

该方程相当于引入扩散张量 $D$ 对Possion方程即 ${\nabla }^{2}Z=\nabla \left(p,q\right)$ 进行了加权。

注意到，等式(2)是通过将

$\{\begin{array}{l}\frac{\partial E}{\partial Z}=0,f_1\left(Z_x,Z_y\right)=d_{11}{Z}_x+d_{21}{Z}_y\\ f_2\left(Z_x,Z_y\right)=d_{12}{Z}_x+d_{22}{Z}_y\\ f_3\left(p,q\right)=d_{11}p+d_{21}q\\ f_4\left(p,q\right)=d_{12}p+d_{22}q\end{array}$ (4)

代入到方程(1)式中获得的。因此，各向异性扩散对应于函数 $f_i$ ， $f_i$ 是关于梯度的仿射变换。与常见方法如Possion方程求解方法、FC算法不同的是，常见方法使用了各向同性扩散为梯度设置了同等的权重，本研究使用各向异性扩散为梯度设置了不等的权重，克服了异常值的影响和保留了更多的特征。虽然这种方法利用了各向异性扩散，但在这个方法中没有时间或迭代的概念。

3. 扩散张量的构造与数值求解

3.1. 扩散张量

在重建曲面方法中使用扩散张量不是新的思想，如Agrawal [5] 将梯度的分量与高斯核进行卷积获得了一个扩散张量，Queau [6] 提出了一个含有未知量高度的扩散张量，但当物体包含尖锐特征时,这些方法是有限的。因此，本研究构造了一个保细节的扩散张量，使用该扩散张量重建出的曲面能够保留尖锐的特征。在每一个像素点处，记矩阵 $T$ 为原始的结构张量， $K_{\sigma }$ 为一个高斯核，尺度为 $\sigma$ 。笔者根据文献 [8] 的尺度参数的选取原则，使用适应尺度参数算法选取了合适的尺度 $\sigma$ ，矩阵 $T$ 表示为：

$T=\left[\begin{array}{cc}{p}^2& pq\\ qp& q^2\end{array}\right]$ (5)

将矩阵 $T$ 与高斯核 $K_{\sigma }$ 进行分量卷积得到一个 $2\times 2$ 的新结构张量 $H$ 。

$H=T\ast K_{\sigma }=\left[\begin{array}{cc}{h}_{11}& h_{12}\\ h_{21}& h_{22}\end{array}\right]$ (6)

记 $v_1$ ， $v_2$ 为结构张量 $H$ 的正交特征向量。记 ${\mu }_1$ ， ${\mu }_2$ 为结构张量 $H$ 的特征值， ${\mu }_1\ge {\mu }_2$ ，对矩阵 $H$ 简单代数求解特征向量与特征值，有

$\{\begin{array}{l}{\mu }_1=\frac{1}{2}\left[h_{11}+h_{22}+\sqrt{{\left(h_{11}-h_{22}\right)}^2+4h_{12}^2}\right]\\ {\mu }_2=\frac{1}{2}\left[h_{11}+h_{22}-\sqrt{{\left(h_{11}-h_{22}\right)}^2+4h_{12}^2}\right]\end{array}$ (7)

$\{\begin{array}{l}{v}_1={\left[2u_{12},h_{22}+h_{11}-\sqrt{{\left(h_{11}-h_{22}\right)}^2+4h_{12}^2}\right]}^{\text{T}}\\ v_2\perp v_1\end{array}$ (8)

向量 $v_1$ 表示高度值波动最大的方向，而 $v_2$ 给出了光滑的首选局部方向。特征值 ${\mu }_1$ 和 ${\mu }_2$ 传递了形状信息。当 ${\mu }_1\ge {\mu }_2\approx 0$ 时，反映的是曲面的线形区域， ${\mu }_1\ge {\mu }_2\gg 0$ 时，反映的是曲面的角落区域 [9] 。由于扩散张量 $D$ 的特征向量应该反映出局部曲面结构，因此，本研究选择 $v_1$ 、 $v_2$ 作为扩散张量 $D$ 的特征向量。 由于使 ${\mu }_1$ 主方向的变化大能够平滑曲面的每个区域和保持曲面的尖锐特征及边缘特征，因此，选择指数函数表示扩散张量 $D$ 的特征值，构造如下：

$\begin{array}{l}{\lambda }_1=\{\begin{array}{ll}1\hfill & {\mu }_1=0\hfill \\ \beta +1-{\text{e}}^{\frac{-3.315}{{\mu }_1^4}}\hfill & {\mu }_1>0\hfill \end{array}\\ {\lambda }_2=1\end{array}$ (9)

其中， ${\lambda }_1$ ， ${\lambda }_2$ 是矩阵 $D$ 的特征值，其反映了扩散强度在各个主方向上的变化。 $\beta \in \left(0,1\right)$ 确保扩散张量 $D$ 的正定性，根据结构张量 $H$ 的特征向量与 ${\lambda }_1$ 和 ${\lambda }_2$ 运用特征分解获得了扩散张量 $D$ 。

$D=\left[v_1,v_2\right]\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]{\left[v_1,v_2\right]}^{-1}$ (10)

3.2. 数值离散化

在像素点 $\left(x,y\right)$ ，记 $u_D=\nabla \left(d_{11}p+d_{21}q,d_{12}p+d_{22}q\right)$ ，网格节点之间的距离为1。采用有限差分近似和二维矩阵的字典排序离散化模型 [10] ，对 $\nabla \left(d_{11}{Z}_x+d_{21}{Z}_y,d_{12}{Z}_x+d_{22}{Z}_y\right)$ 进行离散，则有

$\begin{array}{l}=d_{11}Z\left(x+1,y\right)-d_{11}Z\left(x,y\right)-d_{11}Z\left(x,y\right)+d_{11}Z\left(x-1,y\right)\\ +d_{21}Z\left(x+1,y\right)-d_{21}Z\left(x+1,y-1\right)-d_{21}Z\left(x,y\right)+d_{21}Z\left(x,y-1\right)\\ +d_{12}Z\left(x,y+1\right)-d_{12}Z\left(x-1,y+1\right)-d_{12}Z\left(x,y\right)+d_{12}Z\left(x-1,y\right)\\ +d_{22}Z\left(x,y+1\right)-d_{22}Z\left(x,y\right)-d_{22}Z\left(x,y\right)+d_{22}Z\left(x,y-1\right)\end{array}$ (11)

通过上述的离散公式，同理可得 $u_D$ 为 $u_D$ 在整个图像上的离散，因此，等式(2)式可以被写成

${\nabla }_D^{2}Z=u_D$ (12)

其中， ${\nabla }_D^2$ 可表示为尺寸大小为 $MN\times MN$ 的稀疏矩阵，可称为基于扩散张量 $D$ 的加权拉普拉斯核，如下：

${\nabla }_D^2:=\left[\begin{array}{ccc}0& d_{11}\left(x-1,y\right)+d_{12}\left(x-1,y\right)& -d_{12}\left(x-1,y+1\right)\\ d_{22}\left(x,y-1\right)+d_{21}\left(x,y-1\right)& -\Sigma & d_{22}\left(x,y+1\right)+d_{12}\left(x,y+1\right)\\ -d_{12}\left(x+1,y-1\right)& d_{11}\left(x+1,y\right)+d_{12}\left(x+1,y\right)& 0\end{array}\right]$

将加权拉普拉斯核用矩阵的形式表达，等式(2)式可以写成一个稀疏的线性方程组，记为 $L_{D}Z=u_D$ ，选取的边界条件是诺伊曼边界，方程组的解可直接采用Guass消元法求得，即 $Z=L_D^{-1}{u}_D$ 。

4. 数值实验

本研究从重建曲面的3D形状、一维高度图、重建误差等衡量方法性能，将选取合适的高斯核后的结果与Possion方程 [4] 、Agrawal方法 [5] 的结果进行对比。选取了尺寸大小为64×64的合成斜坡峰作为实验中的重建曲面。在真实曲面的梯度中加入了方差5%的高斯随机噪声和10%均匀分布的异常值，真实梯度场与破坏的梯度场如图1所示。

(a) x方向的真实梯度 (b) y方向的真实梯度 (c) x方向的破坏梯度 (d) y方向的破坏梯度

Figure 1. Gradients in the x and y directions

图1. x和y方向的梯度

将Possion方程以及Agrawal方法的重建结果与本研究方法重建结果进行对比，选择Possion方程的原因在于该方程是各向同性扩散的，会平滑重建曲面的显著特征，通过对比能够反映出各向异性扩散PDE重建模型保持曲面显著特征的优势，选择Agrawal方法的原因在于文献提出的方程是各向异性扩散的，保留了重建曲面的细节，但对于尖锐特征的地方恢复不佳，通过对比能够反映出本研究方法是对Agrawal方法的改进，曲面尖锐特征的恢复较佳，重建误差更小。在无异常值的情况下使用Possion方程、Agrawal方法、本研究方法重建斜坡峰曲面如图2所示。

(a) 真实图 (b) Possion方程 (c) Agrawal方法 (d) 本研究方法

Figure 2. Reconstruction of no outliers

图2. 不存在异常值的重建

图2(a)是合成的真实曲面，图2(b)~(d)是在梯度场中加入了方差为5%的高斯噪声与无异常值使用求解Possion方程的解析解、Agrawal方法中的梯度的仿射变换算法、本研究方法重建的曲面。从图中可以看出，不存在异常值的时候,三种方法的重建效果都佳,对噪声具有鲁棒性。为了验证本研究方法对异常值的鲁棒性和保留更多细节的有效性，在存在异常值和噪声的情况下的重建效果如图3所示。

(a) Possion方程 (b) Agrawal方法 (c) 本研究方法

Figure 3. Reconstruction in presence of noise and outliers

图3. 存在噪声与异常值的重建

图3展示了存在异常值和噪声的情况下三种方法重建的3D形状。梯度存在异常值时，与图2(b)相比，图3(a)重建的斜坡与地面凸起地方较多，表明了Possion方程对异常值不鲁棒；与图2(c)相比，图3(b)在尖锐地方重建效果不佳，表明了Agrawal方法没有考虑尺度参数的选择，构造的扩散张量不能很好地保留尖锐的特征。图3(c)为了保证扩散张量的正定性和避免高斯核尺度过大平滑曲面的细节，设置了 $\beta =0.02,\sigma =0.5$ 。结果表明本研究方法较其它两种方法来说，重建效果更佳，恢复了曲面的尖锐特征，局部细节更清晰，同时减少了噪声。

为了能够更直观地分析方法的有效性和对噪声与异常值的鲁棒性，从各个方法求解的高度值进行分析。抽取Y = 33处重建曲面的信号线进行对比，结果如图4所示。

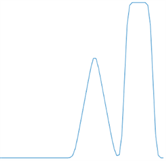(a) 真实高度 (b) Possion方程 (c) Agrawal方法 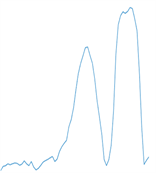(d) 本研究方法

Figure 4. One-D height plot

图4. 一维高度图

图4是扫描线横跨斜坡峰获取的一维高度图，从图中可以看出，Possion方程大致恢复了曲面的形状，但估计的高度值与真实图的高度值相差较大，存在一定的扭曲，Agrawal方法估计尖锐位置的高度偏差较大，与这两种方法相比，本研究方法求出的解更接近于真实值，且保留了曲面的大部分细节。

为了定量地比较本研究方法与其他方法的3D 形状重建结果，使用物体曲面高度的均方误差(Mse)、相对均方误差(Rmse)指标对重建方法进行比较，Mse和Rmse定义为

$E_{Mse}=\frac{1}{M\times N}{\displaystyle \underset{x=1}{\overset{M}{\sum }}{\displaystyle \underset{y=1}{\overset{N}{\sum }}{\left|Z_{xy}-{\tilde{Z}}_{xy}\right|}^2}}$ (13)

$E_{Rmse}=\frac{1}{M\times N}{\left|\frac{{\displaystyle \underset{x=1}{\overset{M}{\sum }}{\displaystyle \underset{y=1}{\overset{N}{\sum }}\left|Z_{xy}-{\tilde{Z}}_{xy}\right|}}}{{\displaystyle \underset{x=1}{\overset{M}{\sum }}{\displaystyle \underset{y=1}{\overset{N}{\sum }}{Z}_{xy}}}}\right|}^2$ (14)

其中， $Z_{xy}$ 为图像像素点 $\left(x,y\right)$ 处真实的高度值， ${\tilde{Z}}_{xy}$ 为比较方法或本研究方法重建的高度值，M、N分别为图像的行数与列数。比较结果见表1。

Table 1. Mean square error and relative mean square error

表1. 均方误差与相对均方误差

从表1可以发现，在无异常值的情况下，三种算法的误差都低。存在异常值时，本研究方法与Possion方程求解方法和Agrawal方法相比明显性地降低了Mse，这是因为本研究选取了合适尺度的高斯核与有效的数值求解方法，虽然Rmse较高，但这在实际应用中是可接受的。

5. 总结

笔者选取合适尺度的高斯核与梯度的Hessian矩阵获得一个保细节的扩散张量，在梯度积分过程中，引入该张量为梯度设置空间变化的各向异性权重，从而建立了一个基于各向异性扩散PDE曲面重建模型，通过求解数值离散后的模型重建出物体的三维形状。比较实验结果表明，与其他方法相比，本研究方法重建效果更佳，且保留了物体的尖锐特征。未来考虑在避免处理边界条件的情况下，使用快速、更有效的算法求解基于各向异性扩散的重建曲面模型。

基金项目

2022年湖南省教育厅科学研究项目(22A0368)，吉首大学校级科研项目(Jdy22012)。

NOTES

^*通讯作者。