函数k(u)=▏sinu▏+a所确定的Wulff形

Wulff Shape Determined by the Function k(u)=▏sinu▏+a

摘要: 凸体是积分几何和凸几何分析的重要内容，Wulff形作为一类特殊凸体，具有一定研究价值。利用凸体的支持函数与函数性质，研究函数k(u)=▏sinu▏+a所确定的Wulff形，给出Wulff形的周长和面积的计算公式。

Abstract: Convex body is an important part of integral geometry and convex geometry analysis. As a special convex body, Wulff shape has certain research value. By using the support functions of convex bod-ies and function properties, this paper discusses the Wulff shape determined by the function k(u)=▏sinu▏+a , given the formula for calculating the perimeter and area of the Wulff shape.

1. 引言与主要结果

积分几何和凸几何分析研究领域涉及广泛，在计算机软件和力学等方面也有广泛应用，凸体是积分几何和凸几何分析学科中的重要研究对象，Wulff形作为特殊凸体值得我们进一步研究。

记 $R^n$ 为 $n\left(n\ge 2\right)$ 维欧氏平面， $S^{n-1}$ 为 $R^n$ 中单位球面， $S^1$ 为 $R^2$ 中单位圆周。设K为 $R^2$ 中点集，如果对任意两点 $x,y\in K$ ， $0\le \lambda \le 1$ ，都有 $\lambda x+\left(1-\lambda \right)y\in K$ ，则称K为凸集。具有非空内点的紧凸集称为凸体。

若K为 $R^2$ 中的凸体，由文献 [1] 得出其支持函数 $h_K\left(u\right)$ 的定义为：

$h_K\left(u\right)=\sup \left\{p:G\left(p,u\right)\cap K\ne \varnothing \right\},$

其中p是平面直角坐标系 $xOy$ 原点o到直线 $G\left(p,u\right)$ 的距离，u是ox轴与过原点又垂直于G的射线的夹角，且直线 $G\left(p,u\right)$ 的广义法式方程为：

$G\left(p,u\right):x\cos u+y\sin u-p=0,$

其中 $\left(x,y\right)$ 是直线 $G\left(p,u\right)$ 上点的坐标。

给出二维欧氏平面 $R^2$ 上一个单参数直线族

$\left\{C_{\alpha }\right\}:F\left(x,y,\alpha \right)=0,$ (1)

其中 $\alpha$ 是参数。当 $\alpha$ 的值变化时，得到族中不同的直线 $C_{\alpha }$ ，并且假定函数 $F\left(x,y,\alpha \right)$ 具有一阶与二阶连续偏导数，则有直线族 $\left\{C_{\alpha }\right\}$ 的包络C满足方程组

$\{\begin{array}{l}F\left(x,y,\alpha \right)=0,\\ F_{\alpha }\left(x,y,\alpha \right)=0.\end{array}$ (2)

关于包络更详细的定义，参见文献 [2] 。

引理1 设曲线C由参数方程

$x=x\left(t\right),y=y\left(t\right),t\in \left[\alpha ,\beta \right]$

给出，在 $\left[\alpha ,\beta \right]$ 上 $y\left(t\right)$ 连续， $x\left(t\right)$ 连续可微且 $x^{\prime }\left(t\right)\ne 0$ (对于 $y\left(t\right)$ 连续可微且 $y^{\prime }\left(t\right)\ne 0$ 的情形可类似地讨论)。记 $a=x\left(\alpha \right),b=x\left(\beta \right)$ ( $a<b$ 或 $b<a$ )，则由曲线C及直线 $x=a,x=b$ 和x轴所围成的图形，其面积计算公式为

$A={\displaystyle {\int }_{\alpha }^{\beta }\left|y\left(t\right)x^{\prime }\left(t\right)\right|\text{d}t}.$ (3)

假设函数 $k_t\left(u\right)=k\left(t,u\right):I\times S^{n-1}\to \left(0,\infty \right)$ 是严格正连续函数，区间 $I\subset R$ ，则对给定的 $t\in I$ ，称

$K_t=\underset{u\in S^{n-1}}{{\displaystyle \cap }}\left\{x\in R^n:x\cdot u\le k\left(t,u\right)\right\}$

是关于函数 $k_t\left(u\right)$ 的Wulff形，且Wulff形是凸体 [3] 。

关于Wulff形的研究已有一些成果。Yi Jun He [4] 借助高斯映射等刻画了Wulff形的新特征；Ai-Jun Li [5] 研究了Wulff形及其极线的截面和投影的体积不等式；Huhe Han [6] 研究了Wulff形和某类凸积分。本文研究对象与其他不同的是选定了一类严格正的特殊连续函数，研究对应Wulff形的形状、周长和面积等。

因函数 $k_t\left(u\right)$ 中的t对此处的研究无影响，于是记函数 $k_t\left(u\right)$ 为 $k\left(u\right)$ ，记Wulff形 $K_t$ 为K，其面积记为 $S_K$ ，周长记为 $L_K$ 。

在 $R^2$ 上，函数 $k\left(u\right):S^1\to \left(0,\infty \right)$ 。取 $k\left(u\right)=\left|\sin u\right|+a$ ，实数 $a>0$ ，显然 $k\left(u\right)$ 是严格正的连续函数，所以由它可以确定一个Wulff形。本文研究了函数 $k\left(u\right)=\left|\sin u\right|+a$ 所确定的Wulff形的相关问题，得到如下主要结果：

定理1 若函数 $k\left(u\right)=\left|\sin u\right|+a$ ，且实数 $a>0$ ，则该函数所确定的Wulff形是操场域，它的两段圆弧分别以点 $\left(0,1\right)$ 和点 $\left(0,-1\right)$ 为圆心，以a为半径。

2. 定理的证明

定理1的证明 给定函数 $k\left(u\right)=\left|\sin u\right|+a\left(a>0\right)$ ，因为它在定义域区间 $u\in \left[0,2\pi \right]$ 上不可导，所以不能直接在 $\left[0,2\pi \right]$ 上通过求导来讨论，又因为不可导的点只有 $u=\pi$ ，于是可将定义域分为 $u\in \left[0,\pi \right]$ 和 $u\in \left[\pi ,2\pi \right]$ 两个部分进行考虑。

在区间 $u\in \left[0,\pi \right]$ 上， $\left|\sin u\right|=\sin u$ ，根据直线 $G\left(k\left(u\right),u\right)$ 的方程是 $x\cos u+y\sin u-k\left(u\right)=0$ ，得到直线族 $\left\{C_u\right\}$ 的方程为：

$\left\{C_u\right\}:x\cos u+y\sin u-\sin u-a=0,$

其中 $u\in \left[0,\pi \right]$ 是参数。代入方程组(2) $\{\begin{array}{l}F\left(x,y,u\right)=0,\\ F_u\left(x,y,u\right)=0,\end{array}$ 得

$\{\begin{array}{l}x\cos u+y\sin u-\sin u-a=0,\\ -x\sin u+y\cos u-\cos u=0,\end{array}$ (4)

根据上式解得

$x=a\cos u,y=a\sin u+1,$

进而有

$x^2+{\left(y-1\right)}^2=a^2,$

它表示以 $\left(0,1\right)$ 为圆心，以a为半径的圆，此圆上的点并不都是Wulff形边界上的点，因为还要考虑

$u\in \left[0,\pi \right]$ 这一限制。在区间 $\left[0,\pi \right]$ 上，当 $u=0$ 时， $x=a$ ， $y=1$ ；当 $u=\frac{\pi }{2}$ 时， $x=0$ ， $y=1+a$ ；当 $u=\pi$

时， $x=-a$ ， $y=1$ ，Wulff形边界的轨迹是连续的，当u从0到 $\pi$ 变化时，满足(4)式的点刚好是以 $\left(0,1\right)$ 为圆心，以a为半径的圆的上半圆弧，它参与构成Wulff形的边界。

同理考虑区间 $u\in \left[\pi ,2\pi \right]$ ，因为 $\left|\sin u\right|=-\sin u$ ，又根据直线 $G\left(k\left(u\right),u\right)$ 的方程是 $x\cos u+y\sin u-k\left(u\right)=0$ ，得到直线族 $\left\{C_u\right\}$ 的方程为：

$\left\{C_u\right\}:x\cos u+y\sin u+\sin u-a=0,$

其中 $u\in \left[\pi ,2\pi \right]$ 是参数。代入方程组(2) $\{\begin{array}{l}F\left(x,y,u\right)=0,\\ F_u\left(x,y,u\right)=0,\end{array}$ 得

$\{\begin{array}{l}x\cos u+y\sin u+\sin u-a=0,\\ -x\sin u+y\cos u+\cos u=0,\end{array}$ (5)

根据上式解得

$x=a\cos u,y=-1+a\sin u,$

进而有

$x^2+{\left(y+1\right)}^2=a^2,$

它表示以 $\left(0,-1\right)$ 为圆心，以a为半径的圆。在讨论的区间 $\left[\pi ,2\pi \right]$ 上，当 $u=\pi$ 时， $x=-a$ ， $y=-1$ ；

当 $u=\frac{3\pi }{2}$ 时， $x=0$ ， $y=-1-a$ ；当 $u=2\pi$ 时， $x=a$ ， $y=-1$ ，Wulff形边界的轨迹是连续的，所以只

有下半圆弧参与构成Wulff形的边界。

再考虑区间端点 $u=0,\pi ,2\pi$ 。当 $u=0$ 时，直线 $G\left(k\left(0\right),0\right)$ 的方程是 $x=a$ ；当 $u=\pi$ 时，直线 $G\left(k\left(\pi \right),\pi \right)$ 的方程是 $x=-a$ ；当 $u=2\pi$ 时，直线 $G\left(k\left(2\pi \right),2\pi \right)$ 的方程是 $x=a$ ，结合Wulff形的定义分析可以知道，直线 $x=-a$ 和直线 $x=a$ 与前面得到的两个半圆弧构成的闭合凸体就是函数 $k\left(u\right)=\left|\sin u\right|+a$ 所确定的Wulff形，是一个操场域，它的两段圆弧分别以点 $\left(0,1\right)$ 和点 $\left(0,-1\right)$ 为圆心，以a为半径。

推论1 若函数 $k\left(u\right)=\left|\sin u\right|+a\left(a>0\right)$ ，K是 $k\left(u\right)$ 所确定的Wulff形，则K的周长 $L_K=2a\pi +4$ ，K的面积 $S_K=a^2\pi +4a$ 。

证明 因为函数 $k\left(u\right)=\left|\sin u\right|+a\left(a>0\right)$ 所确定的Wulff形是由两个半圆和一个矩形组成的操场域，所以通过简单计算容易得到它的面积 $S_K=a^2\pi +4a$ ，周长 $L_K=2a\pi +4$ 。

此外，也可以应用公式(3)计算函数 $k\left(u\right)=\left|\sin u\right|+a$ 所确定的Wulff形的面积，有

$\begin{array}{c}{S}_K={\displaystyle {\int }_0^{\pi }\left|a^2{\sin }^{2}u+a\sin u\right|\text{d}u}+{\displaystyle {\int }_{\pi }^{2\pi }\left|a^2{\sin }^{2}u-a\sin u\right|\text{d}u}\\ =2\left(\frac{\pi a^2}{2}+2a\right)=\pi a^2+4a.\end{array}$

具体取函数 $k\left(u\right)=\left|\sin u\right|+3$ 得到图1如下，在函数 $k\left(u\right)=\left|\sin u\right|+a$ 中将参数a取为其他值，得到图2如下：

图1中所示Wulff形的面积为：

$S_K=3^2\times \pi +4\times 3=12+9\pi .$

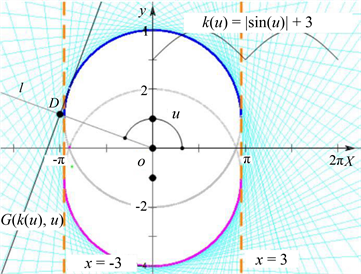
Figure 1. The Wulff shape determined by the function $k\left(u\right)=\left|\sin u\right|+3$

图1. 函数 $k\left(u\right)=\left|\sin u\right|+3$ 所确定的Wulff形

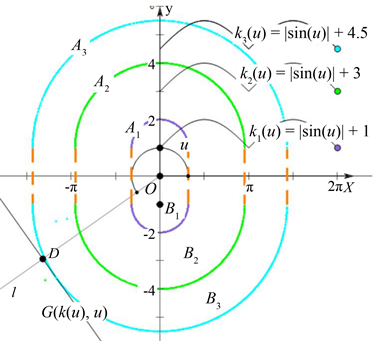
Figure 2. The Wulff shape determined by the function $k\left(u\right)=\left|\sin u\right|+a\left(a=1,3,4,5\right)$

图2. 函数 $k\left(u\right)=\left|\sin u\right|+a\left(a=1,3,4,5\right)$ 所确定的Wulff形

关于函数 $k\left(u\right)=a\left|\sin bu\right|+c$ 所确定的Wulff形是后续的研究内容。基于上述结论，可研究函数 $k\left(u\right)=\left|\cos u\right|+a\left(a>0\right)$ 所确定的Wulff形及其相关性质。