包络与奇解的等价关系探究

A Discussion on the Equivalent Relationship between the Envelop and Singular Solution

摘要: 首先给出现有常微分教材中包络和奇解的几种常见定义，之后给出实例揭示二者之间存在一定关系。接下来针对包络与奇解是等价的这一结论展开研究，具体实例表明：奇解就是包络这一结论的正确性是建立在包络的宽泛定义基础之上的，在严格的包络定义下，二者并不等价。教学过程中须将二者区分对待，不能混淆。

Abstract: This paper firstly introduces several common definitions of envelop and singular solution for ordi-nary differential equations. An example reveals that there exists the relationship between the en-velop and singular solution to some extent. Then the discussion on the equivalence between envel-op and singular solution is carried out. By presenting an example we find that the validity of the conclusion that the singular solution is envelop is based on the broad definition of envelop, and un-der the strict definition of envelop the equivalence of envelop and singular solution doesn’t hold. Therefore, during the process of teaching they must be treated differently and should not be con-fused.

1. 引言

早在1715~1718年间，Taylor B就已开始对常微分方程的奇解、包络和变量代换公式展开研究。1734年，Clairaut重点研究了以其名字命名的Clairaut方程，他发现该方程的通解是一族直线，而这一直线族的包络又是方程的奇解，且该奇解不包含于通解之中。之后Clairaut和Euler对奇解进行了全面的深入研究，给出了利用常微分方程本身求奇解的一般方法。近年来人们意识到包络和奇解存在广阔的研究与应用空间 [1] - [6] ，张少霞 [7] 给出了奇解的几种定义方式，分别指出了各自的利弊；徐丽君等 [8] 讨论了包络和奇解的关系，并给出了求包络的一般方法；王广瓦 [9] 以举反例的方式指出文献 [10] 中结论的不完善。本文进一步研究包络和奇解的等价关系，全文分三部分，第一部分给出包络和奇解的多种定义方式；第二部分讨论包络和奇解之间的关系；第三部分给出一阶显式微分方程不存在奇解的判别方法；第四部分对本文做简单总结。

2. 包络和奇解的关系

2.1. 包络的概念

定义2.1.1 [11] ：对于平面曲线族 $\left\{c_{\alpha }\right\}$ ，若存在曲线E，使得对于E上每个点P，必有曲线族中某一条曲线与E在点P相切，且对于曲线族中每一条曲线 $c_{\alpha }$ ，存在曲线E上一点P，使得 $c_{\alpha }$ 与E在点P相切，我们将具有这种性质的曲线E称作曲线族 $\left\{c_{\alpha }\right\}$ 的包络。

定义2.1.2 [12] ：所谓曲线族的包络是指这样一条曲线，在这曲线上所有的各个点，这条曲线与曲线族中各不同的曲线相切，就是说，在这条曲线上的每一点，这条曲线与曲线族中通过这点的曲线有公共切线。

定义2.1.3 [10] ：曲线族的包络是指这样的曲线，它本身并不包含在曲线族中，但过这曲线的每一点，在曲线族中有一条曲线和它在这点相切。

注意到定义2.1.3要求包络本身不能包含于所研究的曲线族中，而定义2.1.1和定义2.1.2并未对此做出要求。因而上面三种定义是不等价的，本文后面给出的例2也从实际角度验证了这一结论。

2.2. 奇解的概念

在常微分方程所有解对应的积分曲线中，有时会存在一条特殊的不包含于通解所对应的积分曲线族中的积分曲线，在其上的每一点有通解对应的积分曲线族中至少有一条曲线与之在该点相切。例如，

考虑方程 $y={\left(\frac{\text{d}y}{\text{d}x}\right)}^2-x\frac{\text{d}y}{\text{d}x}+\frac{x^2}{2}$ ，其通解为 $y=\frac{x^2}{2}+cx+c^2$ (c是任意常数)，此外还有一个特解 $y=\frac{x^2}{4}$ ，注

意到该特解不含于通解中，但过其上每一点都与通解对应的积分曲线族中的某一条积分曲线相切，如

图1所示。在几何学上，这条特殊的曲线称为上述曲线族的包络；在微分方程理论中，我们称 $y=\frac{x^2}{4}$ 为

方程的奇解。

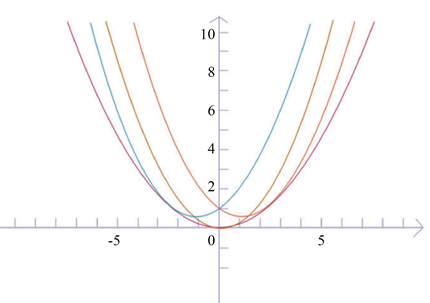
Figure 1. $y=\frac{x^2}{4}$ is the singular solution of the equation

图1. $y=\frac{x^2}{4}$ 为方程的奇解

定义2.2.1 [13] ：如果常微分方程 $F\left(x,y,y^{\prime }\right)=0$ 的某个特解对应的积分曲线满足以下条件：过其上每一点都存在方程的不同的积分曲线与之在该点相切，并且此相切的积分曲线在切点的任何邻域内都不重合，则称此特解为微分方程的奇解。

定义2.2.2 [11] ：若存在方程 $F\left(x,y,y^{\prime }\right)=0$ 的某个解，在它所对应的积分曲线上每点处都不满足解的存在唯一性，即解的唯一性都被破坏，则称此解为方程的奇解。

我们利用积分曲线族和方程解的唯一性遭到破坏这两种方式给出了奇解定义，从定义不难发现，奇解首先是方程的解，只不过它和方程的其它解存在特殊的位置关系。

2.3. 包络和奇解的关系探讨

我们先来看一个具体的问题。

例1：求方程 ${\left(\frac{\text{d}y}{\text{d}x}\right)}^2+y^2-1=0$ 的奇解。

解：我们利用求奇解的方法 [7] [10] ，从方程组 $\{\begin{array}{l}{p}^2+y^2-1=0\\ 2p=0\end{array}$ 中消p得到p-判别曲线 $y=\pm 1$ ，容易验

证 $y=\pm 1$ 是方程的解；又可求得原方程的通解为 $y=\sin \left(x+c\right)$ ，c是任意常数，利用定义2.2.1容易验证 $y=\pm 1$ 是微分方程的奇解。

从几何角度看，上例中 $y=\pm 1$ 对应的积分曲线恰好是通解对应的积分曲线族的包络，如下图2所示。

上例注意到了奇解和包络在几何意义上的相通性，在求方程奇解的同时得到了方程通解对应的积分曲线族的包络。从奇解定义出发，我们不难得出如下结论：一阶微分方程通解对应的积分曲线族的包络(如

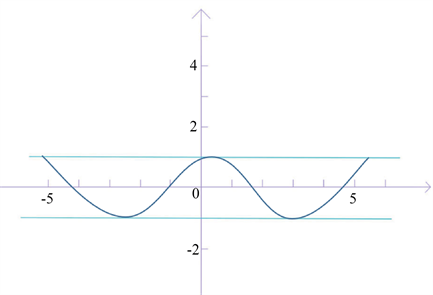
Figure 2. $y=\pm 1$ is the envelope of $y=\sin \left(x+c\right)$

图2. $y=\pm 1$ 是 $y=\sin \left(x+c\right)$ 的包络

果存在的话)一定是方程的奇解。部分教材将这个结论的逆命题作为结论直接给出，即微分方程的奇解(如果存在的话)对应的积分曲线也是微分方程通解对应的积分曲线族的包络。但是在包络定义2.1.3的框架下，该结论的正确性值得商榷，我们看下面的例子。

例2：求 ${y^{\prime }}^3-4xy{y}^{\prime }+8y^2=0$ 的奇解。

解：利用一阶隐式微分方程的求解方法，易得方程通解为 $y=c{\left(x-c\right)}^2$ ，其中c为任意常数，特解为

$y=\frac{4}{27}{x}^3$ 。考虑 $y=0$ 这个特解，显然根据奇解定义2.2.1和定义2.2.2， $y=0$ 是方程的奇解。下面考查这

个奇解对应的积分曲线是否为方程通解对应的积分曲线族的包络。任取曲线 $y=0$ 上一点 $\left(x_0,0\right)$ ，我们发现，过该点都能从通解对应的积分曲线族中找到一曲线 $y=x_0{\left(x-x_0\right)}^2$ ，使得 $y=0$ 与 $y=x_0{\left(x-x_0\right)}^2$ 在 $\left(x_0,0\right)$ 点相切，但是根据定义2.1.3，由于曲线 $y=0$ 包含在积分曲线族 $y=c{\left(x-c\right)}^2$ 中( $c=0$ 的情况)，故它不是积分曲线族 $y=c{\left(x-c\right)}^2$ 中的包络。由此我们得出奇解未必是包络的结论。注意到如果我们依据定义2.1.1和定义2.1.2来定义包络，则显然奇解 $y=0$ 对应的曲线是方程通解对应的积分曲线族的包络。

正如我们已经指出的，本文第二部分给出的包络的三种定义并非是等价关系，定义2.1.3要求更严格，它要求包络对应的曲线一定不能包含在相应的曲线族中。换句话说，定义2.1.3包含在定义2.1.1和定义2.1.2中，而定义2.1.1和定义2.1.2却不能包含在定义2.1.3中。鉴于包络概念的不一致性，所以用求通解对应积分曲线族的包络的方法来求方程的奇解具有一定的局限性，出现这种问题的原因在于奇解的两个等价概念中并没有要求奇解对应的曲线一定不包含在通解对应的积分曲线族中。因此单纯从定义的角度出发，我们也能得出曲线族的包络一定是奇解，奇解不一定是曲线族包络这一结论，这也说明奇解的概念比包络的概念更广一些。因此我们在求方程奇解时要做到具体问题具体分析，不能单纯依赖求包络找奇解，需要恰当方法的灵活运用。

此外，从教学角度看，对于同一个概念给出两种不等价的定义方式是不严格的，即使在不同的场合、不同的应用背景下可以接受这种不等价性，但是对于培养学生数学思维的严谨性是极为不利的。尤其是有一部分教材进一步利用包络的概念来定义奇解(如把奇解定义为微分方程通解对应的积分曲线族的包络)是不恰当的，会在很大程度上引起概念的混淆和自相矛盾，破坏数学的严谨性。因此教材的编撰者应尽早对教材中不合适的定义概念给予修正。

3. 一阶方程 $y^{\prime }=f\left(x,y\right)$ 不存在奇解的判别方法

通过常微分方程中解的存在唯一性内容的学习，我们知道若方程 $\frac{\text{d}y}{\text{d}x}=f\left(x,y\right)$ 的右端函数 $f\left(x,y\right)$ 在

区域 $D\subseteq R^2$ 上有定义， $f\left(x,y\right)$ 在D上连续并且 ${f^{\prime }}_y\left(x,y\right)$ 在D上有界(或连续)，那么方程过区域D内任一点的解是存在且唯一的，从而在D内一定不存在奇解。下面通过一个具体的例题说明如何利用存在唯一性定理判别方程不存在奇解。

例3：判断下列方程是否存在奇解。

(1) $\frac{\text{d}y}{\text{d}x}=e^x+\sin y$ (2) $\frac{\text{d}y}{\text{d}x}=\sqrt{y-2x}+3$

解：(1) 由于 $f\left(x,y\right)=e^x+\sin y$ 及 ${f^{\prime }}_y=\cos y$ 在全平面连续，故方程(1)无奇解。

(2) 注意到 $f\left(x,y\right)=\sqrt{y-2x}+3$ ，它在区域 $y\ge 2x$ 上有定义且连续，而 ${f^{\prime }}_y=\frac{1}{2\sqrt{y-2x}}$ 在 $y>2x$ 上有

定义且连续，故不满足存在唯一性定理条件的点集只有 $\left\{\left(x,y\right)|y=2x\right\}$ ，即方程(2)若有奇解，必定是 $y=2x$ ，然而经验证 $y=2x$ 不是方程的解，从而方程(2)无奇解。

4. 结论

根据奇解和包络的不同定义方式，我们得出如下结论：一阶微分方程通解的包络(如果存在的话)一定是奇解；反之，微分方程的奇解未必是微分方程通解对应曲线族的包络。常微分方程中的包络与奇解不是等同的概念，不能将二者混为一谈，否则会造成衍生结论的自相矛盾，同时破坏了数学概念和逻辑的严密性。

基金项目

国家自然科学基金项目(61877032)。

NOTES

^*通讯作者。