1. 引言
近年来,随着交通建设规模的不断扩大和桥梁使用年限的逐渐增长,桥梁运营风险评估备受关注。传统的评估方法存在一定局限性,如主观性强、不确定性高等问题。因此,学者们开始探索更为科学和客观的评估方法。层次分析法是一种较为广泛应用的方法,但其在赋权过程中存在着一定的主观性和不可靠性。陈红等认为,针对运营期间桥梁的风险评估方法大致有:外观调查法、荷载试验方法、专家评分法、模糊综合评价法、层次分析法几种,单独采用一种方法存在信息量少、较主观、费用较高、不能保证评估结果的准确性等问题 [1] 。吴伟东等针对装配式建筑项目实施阶段的质量风险因素进行识别,采用三角模糊数引入层次分析法计算各指标权重,结果显示运营维护阶段权重要高于施工建设阶段,且运营维护阶段的质量风险较为明显突出 [2] 。张荣凤等通过探究目前运营期桥梁风险评估的研究状况,发现桥梁风险研究起于船撞风险,现已在设计阶段出现规避风险的设计规范,运营期间相关评估理论较丰富;车桥相撞以及超载风险相关研究较少,需要进一步完善相关理论;多因素风险更加符合现实中桥梁所面临的风险,需要进一步研究形成风险评估体系 [3] 。Tempa K利用AHP (层次分析法)对不丹历史上的洪水事件进行地区洪水脆弱性评估,通过对指标的优先级排序,使用基于指标的加权方法绘制了不丹地区洪水脆弱性指数地图,研究发现,脆弱性指数高的地区,与每年极端气候条件相关的此类洪水事件再次发生的可能性非常大 [4] 。Karimi S等通过对不同方法和理论的桥梁结构损伤识别的文献进行批判性回顾,发现不同方法存在差距。这项研究为更准确地识别桥梁结构损伤的方法提供了指导,并为其他研究人员和未来的工作提供了良好的参考 [5] ,这对于延长桥梁使用寿命和保持安全具有重要意义。综上所述,桥梁运营风险评估方法的研究已经取得了一定的进展,但仍有待进一步完善和发展。
2. 层次分析法
层次分析法(Analytic Hierarchy Process,简称AHP)是美国运筹学家T. L. Saaty于1970年提出的一种主观赋权评价方法。是指在处理多目标、多决策等复杂问题时,通过建立层次结构模型,将众多评估指标要素分层分类,进行定量分析,最后得到各层次权重的决策分析方法。由于其系统性、实用性和简洁性等特点,该决策分析方法的使用越来越普遍。近年来,随着层次分析法在桥梁工程风险管理过程中的应用不断成熟和发展,该方法将广泛应用于风险识别、评估、控制和监视等方面。
2.1. 层次分析法的局限性
层次分析法可以将复杂的决策问题分解成一系列子问题,以便更好地理解和解决问题,并且可以根据权重确定最终的决策结果,从而更好地满足决策者的需求。但是,传统层次分析法的赋权过程主观性太强,易受到专家个人偏好的影响,且按1~9标度构造的判断矩阵,不仅计算繁琐,权重可靠性低,而且构造的判断矩阵可能无法通过一致性检验。近年来,人们提出通过修改标度来矫正判断矩阵,如表1所示,即选择合适标度后调整矩阵元素,将无法通过一致性检验的判断矩阵更改为具有满意一致性的判断矩阵,但是这种方法显然违背专家本意,即使判断矩阵通过一致性检验,得到的权重可靠性也很低,无法达到主观评估目的。

Table 1. Meaning of common scale values
表1. 常用标度值含义
关于使用层次分析法常用标度值构建判断矩阵时的局限性,举例说明如下:对于方案A、B、C,若A比B绝对重要,B比C绝对重要,则按照1~9标度可知,
,
,按照逻辑数学的传递性,A比C绝对绝对重要,但是1~9标度并没有“绝对绝对重要”的标度值,因此只能取
,此时
,即B和C同等重要,与主观条件矛盾。
对于按1~9标度构建的判断矩阵R,其最大特征值λmax = 3.5608,一致性指标CI = 0.2814,一致性比例CR = 0.48 > 0.1;对于按比例标度构建的判断矩阵R',其最大特征值为λmax = 3.0385,一致性指标为CI = 0.1925,一致性比例为CR = 0.33 > 0.1。
因此,当采用传统比例标度、指数标度或9/9~9/1分数标度构建判断矩阵时,均存在无法通过一致性检验的情况,此时得到的最大特征值对应的特征向量在权重值计算时也不具备参考价值。
本文基于标度扩展法构造判断矩阵 [6] ,这种方法可以保证构建的判断矩阵完全一致,不需要进行一致性检验,排序向量也可以轻松获得,这样可以大大提高层次分析法决策的可靠性,同时也简化了计算过程,使其更加快捷方便。
2.2. 标度扩展法构造判断矩阵
标度扩展法构造判断矩阵的基本思想:对于风险评估清单列出的n个评价指标
,首先进行两两比较,并按照重要程度的不减方式排序,假设n个指标的重要性排序为
,然后对
与
进行比较,并将对应的标度值记为
,最后按照方案间重要程度的传递性计算出判断矩阵中其他元素的值,从而得到由标度扩展法构造的判断矩阵R。
为了确定由标度扩展法构造的判断矩阵R是否满足一致性检验,需要计算判断矩阵的随机一致性比例CR,即比较判断矩阵的一致性指标CI与同阶的平均随机一致性指标的比值RI,以确定判断矩阵的一致性水平。其中RI的取值如表2所示。
(1)
一般地,当一致性比率CR < 0.1时,则认为判断矩阵有满意的一致性,基本符合完全一致性条件,如果CR > 0.1,则要重新调整判断矩阵,直到符合完全一致性条件。
对于由标度扩展法构造的判断矩阵R,为任意两行成比例的正互反矩阵,则矩阵R的最大特征值等于矩阵的迹,即λmax = n,一致性指标CI = 0,一致性比例CR = 0 < 0.1,因此,在改进层次分析法模型构建时,对于标度扩展法构造的判断矩阵,不再需要进行一致性检验。
2.3. 标度扩展法构造判断矩阵
步骤1:构建评价指标
在建立风险指标体系的层次结构时,需要细致地分析各个风险因素,并将它们按照相应的层次结构进行划分,以便更好地描述各层次间的递阶结构以及因素的从属关系。最高层(目标层)描述了决策者想要达到的目标;中间层(一级指标层)描述了实现目标的具体步骤;最底层(二级指标层)描述了实现步骤的具体细节,AHP层次结构模型如下图1所示。
步骤2:根据标度扩展法构造打分表
在运用层次分析法计算各指标主观权重之前,需要事先整理好同级标度扩展表构建判断矩阵时所需要的数据打分表,并发给相关方面的专家,各专家根据自身经验对重要性排序为
的n个评估指标,按
与
进行两两比较,并对应比例标度表进行指标重要性打分。
步骤3:构造判断矩阵
整理风险指标重要性问卷,按照方案间重要程度的传递性计算出判断矩阵中其他元素的值,依次构造出评价指标的判断矩阵(如表3、表4)。
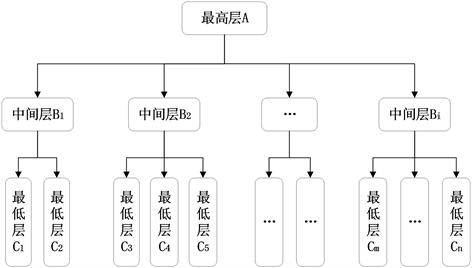
Figure 1. The hierarchical model of AHP
图1. AHP层次结构模型

Table 3. Judgment matrix A-B of the first level indicator layer
表3. 一级指标层判断矩阵A-B

Table 4. Judgment matrix Bi-C for the second level indicator layer
表4. 二级指标层判断矩阵Bi-C
步骤4:计算指标主观权重
指标权重的计算可以通过求解判断矩阵的特征根和特征向量来实现,即求解判断矩阵的特征值和特征向量,其中最大特征值λmax对应的特征向量
就是指标主观权重值。对
向量进行标准化记为
,即为第i项指标的权重值。对于标度扩展法构造的判断矩阵,不再需要进行一致性检验,可根据权重公式直接计算出判断矩阵R中各项指标的权重值:
其中,
为第i项指标的权重值,
表示矩阵R中第i行所有元素的乘积。
3. RM桥梁工程运营风险评估
3.1. 构建风险评估指标体系
本文在对桥梁工程运营风险指标进行识别时,首先通过对相关文献阅读整理 [7] - [15] ,识别出桥梁运营阶段可能遇到的风险指标56种;其次归并语义相近的风险因素并规范表达得到风险指标20种;然后邀请5位长期参与RM桥梁质检的检测工程师和5位资深桥梁养护工程师,通过网上问卷平台问卷星,以电子问卷的形式,发放20份调查问卷,让他们对桥梁初始风险清单问题的影响程度I和发生概率P进行打分;最后去掉可以忽略的风险因素,并构建风险识别清单,根据系统安全理论的观点,将RM桥梁运营阶段风险指标划分为自然风险、人为风险、管理风险。根据RM桥梁风险识别清单构建桥梁风险评估指标体系,共计3个一级指标,13个二级指标,如下图2所示。
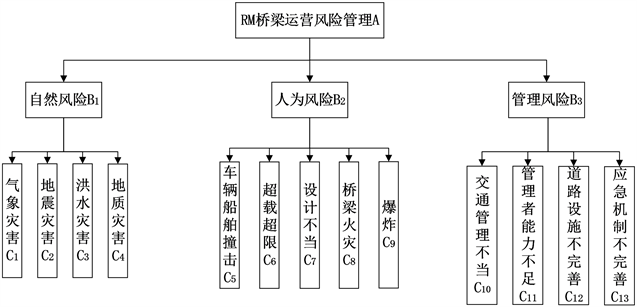
Figure 2. Risk assessment index system for RM bridges
图2. RM桥梁风险评估指标体系
3.2. 评价指标权重计算
通过对检测工程师和养护工程师对桥梁风险指标风险度的打分数据进行信度分析,可以在利用标度扩展法构造判断矩阵之前得到RM桥梁各级指标的重要性排序。故在邀请相关专家根据自身经验结合比例标度对指标
与
进行两两比较打分时,可尽最大可能保证数据的准确性与可靠性,从而按照方案间重要程度的传递性计算出判断矩阵中其他元素的值,整理桥梁运营风险管理一级指标层两两对比关系表(表5),构造出一级指标的判断矩阵
。

Table 5. Comparison table of risk management factors for bridge operations
表5. 桥梁运营风险管理因素对比表
则标度扩展法构造的判断矩阵:
桥梁运营风险管理一级指标重要性排序:B2 > B1 > B3,得RM桥梁运营风险管理体系一级指标权重向量为
,对权重向量归一化得
。
对于RM桥梁风险评估指标体系的13个二级指标权重,其算法与一级指标权重相同,通过计算可以得出(结果如图3):
桥梁自然风险二级指标重要性排序:C4 > C3 > C2 > C1,自然风险二级指标权重向量为
,归一化得
。
桥梁人为风险二级指标重要性排序:C7 > C6 > C5 > C8 > C9,人为风险二级指标权重向量为
,归一化得
。
桥梁管理风险二级指标重要性排序:C12 > C10 > C13 > C11,管理风险二级指标权重向量为
,归一化得
。
标度扩展法构造的判断矩阵R满足一致性检验,因此本章所得各一级指标和二级指标的判断矩阵不再进行一致性检验。
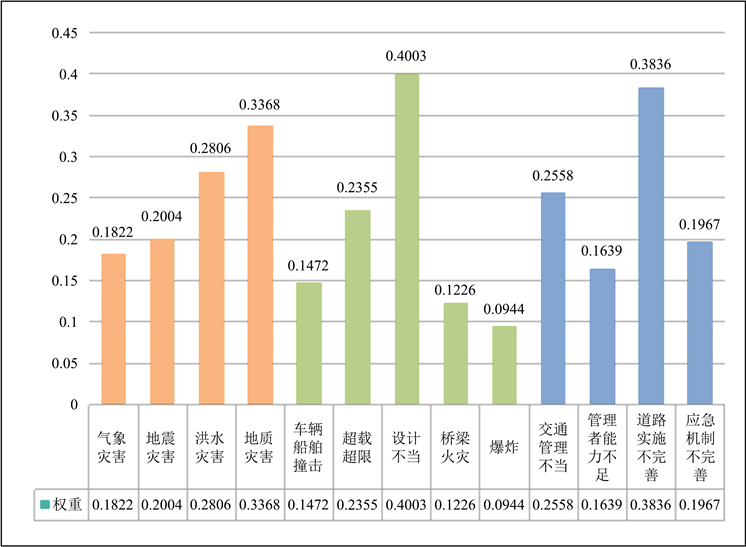
Figure 3. Comparison of weight values of RM bridge risk assessment indicators
图3. RM桥梁风险评估指标权重值对比
4. 结语
本文采用标度扩展法构造层次分析法的判断矩阵,构建RM桥梁运营阶段风险评估的层次结构模型,与传统层次分析法相比,更有利于专家判断打分,计算过程有所减少,权重可靠性高,而且构造的判断矩阵不需要一致性检验。能够较好地从各级风险指标中判别主要因素,有利于桥梁运营阶段风险评估指标的量化。
根据RM桥梁风险指标的评估结果可以看出:自然灾害、人为因素和管理方面的风险都对桥梁安全造成了不同程度的影响。其中,“洪水灾害”和“地质灾害”的权重较高,意味着桥梁建设和维护时需要考虑洪水和地质灾害的可能性,采取相应的防范措施。在人为因素方面,“设计不当”的权重最高,这表明桥梁设计中需要充分考虑各种可能的情况和风险,制定合理的设计方案,确保桥梁的安全性和可靠性。此外,“超载超限”也是一个重要的人为因素,需要采取相应的措施,确保桥梁不受过度负荷的影响。在管理方面,“道路实施不完善”的权重最高,这意味着需要加强对道路的管理和维护,确保道路的质量和安全性,避免因道路问题导致的意外事故。此外,“应急机制的完善”也非常重要,需要建立健全的应急预案和机制,及时处理各种突发事件,减少对桥梁安全带来的影响。
综上所述,运用改进层次分析法对RM桥梁风险指标的评估结果为我们提供了重要的参考和指导,可以帮助我们更好地了解桥梁面临的风险和威胁,采取相应的措施,确保桥梁的安全和可靠性。