基于弹性升阶变换法的一类可化为合流超几何方程的一阶非线性常微分方程的求解

Solving a Class of First-Order Nonlinear Ordinary Differential Equations Which Can Be Transformed into Confluent Hypergeometric Equation Based on Elastic Upgrading Transformation Method

摘要: 根据弹性的可分析一个变量对另一个变量的相对变化率的特性，本文创新性的引进了一种微分变换——弹性升阶变换，用于解决一类一阶非线性常微分方程的求解问题；它可将一阶非线性常微分方程转化为合流超几何方程，从而求得其解；并归纳总结出可扩展应用该方法的解题步骤。该方法为某些一阶非线性常微分方程的求解提供了一种新方法，从而扩大了微分方程的可解类。

Abstract: According to the characteristic of elasticity that can analyze the relative rate of change of one var-iable to another, this paper innovatively introduces a differential transformation, the elastic up-grading transformation, for solving a class of first-order nonlinear ordinary differential equations. It can transform the first-order nonlinear ordinary differential equation into a confluent hypergeometric equation, and thus find its solution, and summarize the steps of applying the method to solve the problems. This method provides a new method for solving some first-order nonlinear ordinary differential equations, so that the solvable type of differential equations is expanded.

1. 引言

众所周知，弹性理论最早是由英国著名经济学家马歇尔 [1] 首次提出，用于解释价格与需求的关系，在经济学中广泛运用，并占有重要的地位。弹性表达式由Woods [2] 提出用于代谢控制系统的分析。近年来，很多学者 [3] [4] 将弹性在物理学、经济学等领域中的应用进行了广泛研究。但是弹性能否用于求解常微分方程呢？

在通常的文献中 [5] [6] ，已有许多常微分方程的求解方法，如：分离变量法，积分因子法，常数变易法等。但是这些方法都只能用于求解某些常见的常微分方程，因此寻求更多的非线性微分方程的求解方法，成为了数学和物理学科中的热点课题。

利用积分变换求解微分方程也是一种大家公认的有效的方法之一，许多学者对其进行了广泛的研究。Ahmed [7] 等人运用指数形式的积分函数变换，求解了二阶线性常微分方程的通解，并将其推广到了一般的二阶常微分方程的求解中；Maitama [8] 等人提出了一种Laplace型积分变换Shehu变换，用于求解常微分方程和偏微分方程；Atangana等人 [9] 提出了一种新的积分变换算子，并运用该积分变换算子得到了一类含有奇异性的分数阶常微分方程和偏微分方程的解；Kim [10] 利用积分和Laplace变换验证了变系数常微分方程的解的形式，并为建立一般的积分变换理论提出了一点思考。Fatoorehchi等人 [11] 研究了非线性常微分方程的解，并运用扩展的Laplace变换得到了Riccati方程、Clairaut’s方程、Blasius方程的解。Fatoorehchi [12] 等人采用扩展Laplace变换研究了Thomas-Fermi方程，并得到了方程的半解析、半数值的解。

利用微分变换求解常微分方程也是一种有用的方法，也有多名学者在这方面做了相关的研究。虞继敏等人 [13] 通过变量代换，其实质也是一种微分变换，将三阶变系数常微分转化为微分方程组，结合刘维尔公式得到了三阶变系数常微分方程的通解；Agboola等人 [14] 研究了三阶常微分方程的初值问题，并应用基于泰勒级数的微分变换得到了三阶常微分方程初值问题的解；Badani [15] 采用一种微分变换得到了任意二阶和三阶线性非齐次常微分方程以及二阶非齐次柯西–欧拉方程的积分型闭型解，并将该方法应用于求解n阶线性非齐次常微分方程。

大家共知，积分变换中的Fourier变换具有强烈的实际应用背景，而微分变换中是否也存在相当的具有实际应用背景的某种变换呢？目前已有相关学者尝试利用弹性变换法对微分方程进行求解，但是他们只是针对Laguerre方程、Chebyshev方程和Legendre方程等进行了研究 [16] [17] [18] [19] 。本文从研究弹性的微分性质出发，引入了一种新的微分变换——弹性升阶变换，创新性地将其应用于求解一类可化为合流超几何方程的一阶非线性常微分方程。

文章结构如下：首先给出了弹性的微分性质以及关于合流超几何方程的知识；其次给出并证明了本文的主要定理；然后归纳总结出弹性升阶变换求解步骤；紧接着将归纳总结出的弹性升阶变换求解步骤进行举例应用；最后对论文做出了总结和进一步的认识。

2. 预备知识

定义1 对于可微函数 $y=f\left(x\right)$ ，且 $f\left(x\right)\ne 0$ 有

$\eta =\frac{x}{y}\frac{\text{d}y}{\text{d}x}$ (1)

其中 $\eta$ 称为 $y=f\left(x\right)$ 相对于x的弹性函数，它在某点 $x_0$ 的值称为弹性系数，记作 ${\eta }_{x_0}$ 。

引理1 若 $\eta$ 为 $y=f\left(x\right)$ 相对于x的弹性函数，且 $f\left(x\right)\ne 0$ 二阶可微，则有

${\eta }^{\prime }=\frac{x}{y}{y}^{″}-\frac{x}{y^2}{\left(y^{\prime }\right)}^2+\frac{1}{y}{y}^{\prime }$ (2)

证明 由定义1知

$\eta =\frac{x}{y}\frac{\text{d}y}{\text{d}x}$

从而有

$\begin{array}{c}{\eta }^{\prime }=\frac{\text{d}\eta }{\text{d}x}=\frac{\text{d}}{\text{d}x}\left(\frac{x}{y}\frac{\text{d}y}{\text{d}x}\right)=\frac{y-x{y}^{\prime }}{y^2}{y}^{\prime }+\frac{x}{y}{y}^{″}\\ =\frac{x}{y}{y}^{″}-\frac{x}{y^2}{\left(y^{\prime }\right)}^2+\frac{1}{y}{y}^{\prime }\end{array}$

即引理1得证。

引理2 合流超几何方程

$x{y}^{″}+\left(\gamma -x\right)y^{\prime }-\alpha y=0$ (3)

其中 $\alpha$ 为参数， $\gamma \ne$ 整数。其通解为：

$y=AF\left(\alpha ,\gamma ,x\right)+B{x}^{1-\gamma }F\left(\alpha +1-\gamma ,2-\gamma ,x\right)$ (4)

其中 $A,B$ 为常数，且 $B\ne 0$ 。 $F\left(\alpha ,\gamma ,x\right)$ 为第一类合流超几何函数，可以表示为

$F\left(\alpha ,\gamma ,x\right)={\displaystyle \underset{k=0}{\overset{\infty }{\sum }}\frac{{\left(\alpha \right)}_k}{k!{\left(\gamma \right)}_k}{x}^k}$

其中 ${\left(\alpha \right)}_k=\alpha \left(\alpha +1\right)\cdots \left(\alpha +k-1\right)$ ，且 ${\left(\alpha \right)}_0=1$ 。特别地， $\alpha =\gamma$ 时有 $F\left(\alpha ,\alpha ,x\right)={\text{e}}^x$ 。

证明 见参考文献 [20] 。

引理3 合流超几何函数的微分性质

$\frac{\text{d}}{\text{d}x}F\left(\alpha ,\gamma ,x\right)=\frac{\alpha }{\gamma }F\left(\alpha +1,\gamma +1,x\right)$

证明 见参考文献 [20] 。

3. 主要定理及其证明

定理1 形如

$x{z}^{\prime }+z^2+\left(\gamma -x-1\right)z-\alpha x=0$ (5)

一阶非线性常微分方程，其中 $\alpha$ 为参数， $\gamma \ne$ 整数，它的解可以表示为：

$z=\frac{x\left[C\frac{\alpha }{\gamma }F\left(\alpha +1,\gamma +1,x\right)+\left(1-\gamma \right)x^{-\gamma }F\left(\alpha +1-\gamma ,1-\gamma ,x\right)\right]}{CF\left(\alpha ,\gamma ,x\right)+x^{1-\gamma }F\left(\alpha +1-\gamma ,2-\gamma ,x\right)}$ (6)

其中C为常数。

证明 对于一阶非线性常微分方程

$x{z}^{\prime }+z^2+\left(\gamma -x-1\right)z-\alpha x=0$

首先，对其做微分变换，令

$z=\frac{x}{y}\frac{\text{d}y}{\text{d}x},y\ne 0$

其中y为关于x的函数。对z求关于x的导数可以得到

$z^{\prime }=\frac{x}{y}{y}^{″}-{\left(\frac{y^{\prime }}{y}\right)}^{2}x+\frac{y^{\prime }}{y}$ (7)

然后，将(7)式带入原方程，可得

$x{y}^{″}+\left(\gamma -x\right)y^{\prime }-\alpha y=0$ (8)

由引理2知(8)式为以 $\alpha$ 为参数， $\gamma \ne$ 整数的合流超几何方程。像这种z关于x的一阶常微分方程，若把z当作另外一个变量y的弹性，则可以将z关于x的一阶非线性常微分方程转化为y关于x的二阶线性常微分方程，这即是所谓的弹性升阶变换的思想。

再由引理2知合流超几何方程的通解为

$y=AF\left(\alpha ,\gamma ,x\right)+B{x}^{1-\gamma }F\left(\alpha +1-\gamma ,2-\gamma ,x\right)$

其中 $A,B$ 为常数且 $B\ne 0$ 。

最后，由于 $z=\frac{x}{y}\frac{\text{d}y}{\text{d}x}$ ，即可得到原方程的通解为

$z=\frac{x\frac{\text{d}\left[AF\left(\alpha ,\gamma ,x\right)+B{x}^{1-\gamma }F\left(\alpha +1-\gamma ,2-\gamma ,x\right)\right]}{\text{d}x}}{AF\left(\alpha ,\gamma ,x\right)+B{x}^{1-\gamma }F\left(\alpha +1-\gamma ,2-\gamma ,x\right)}$ (9)

通过引理3对(9)式进行化简得

$z=\frac{x\left[C\frac{\alpha }{\gamma }F\left(\alpha +1,\gamma +1,x\right)+\left(1-\gamma \right)x^{-\gamma }F\left(\alpha +1-\gamma ,1-\gamma ,x\right)\right]}{CF\left(\alpha ,\gamma ,x\right)+x^{1-\gamma }F\left(\alpha +1-\gamma ,2-\gamma ,x\right)}$

其中C为常数，且 $C=\frac{A}{B},B\ne 0$ 。

即定理1得证。

4. 弹性升阶变换求解步骤

通过对定理1的证明，我们可以归纳总结出利用弹性升阶变换法求解一类可化为合流超几何方程的一阶非线性常微分方程的求解步骤：

第一步：判断所求方程是否为形如(5)式的一阶非线性常微分方程；

第二步：利用弹性升阶变换法令 $z=\frac{x}{y}\frac{\text{d}y}{\text{d}x},y\ne 0$ ，并求出 $z^{\prime }$ ；

第三步：将 $z,z^{\prime }$ 带入到原一阶非线性常微分方程，将其转化为合流超几何方程；

第四步：通过引理2求得合流超几何方程的通解；

第五步：对合流超几何方程的解求弹性，即得到原一阶非线性常微分方程的通解。

通过以上的求解步骤，可以得到如下的基于弹性升阶变换法求解一类可化为河流超比方程的一阶非线性常微分方程的求解流程图(图1)：

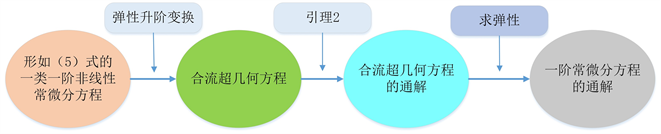
Figure 1. Upgrading transformation method solution flow chart

图1. 弹性升阶变换求解流程图

5. 举例

求解下列一阶非线性常微分方程的通解

$x{z}^{\prime }+z^2-\left(x+\frac{1}{2}\right)z-x=0$ (10)

第一步：容易知道(10)式为形如(5)式的一阶非线性常微分方程。

第二步：利用弹性升阶变换法，令

$z=\frac{x}{y}\frac{\text{d}y}{\text{d}x},y\ne 0$ (11)

并求得

$z^{\prime }=\frac{x}{y}{y}^{″}-{\left(\frac{y^{\prime }}{y}\right)}^{2}x+\frac{y^{\prime }}{y}$ (12)

第三步：将(11)、(12)式代入(10)式，则可以将z关于x的一阶非线性常微分方程转化为y关于x的二阶线性常微分方程

$x{y}^{″}+\left(\frac{1}{2}-x\right)y^{\prime }-y=0$ (13)

通过引理2容易知道(13)式为 $\alpha =1,\gamma =\frac{1}{2}$ 的合流超几何方程。

第四步：通过引理2知(13)式的通解为

$\begin{array}{c}y=AF\left(1,\frac{1}{2},x\right)+B\sqrt{x}F\left(\frac{3}{2},\frac{3}{2},x\right)\\ =AF\left(1,\frac{1}{2},x\right)+B\sqrt{x}{\text{e}}^x\end{array}$ (14)

其中 $A,B$ 为常数，且 $B\ne 0$ 。

第五步：对合流超几何方程的解求弹性，即 $z=\frac{x}{y}\frac{\text{d}y}{\text{d}x}$ ，则可以得到原一阶非线性常微分方程的通解为

$\begin{array}{c}z=\frac{2AxF\left(2,\frac{3}{2},x\right)+B\sqrt{x}{\text{e}}^x\left(\frac{1}{2}+x\right)}{AF\left(1,\frac{1}{2},x\right)+B\sqrt{x}{\text{e}}^x}\\ =\frac{4CxF\left(2,\frac{3}{2},x\right)+\sqrt{x}{\text{e}}^x\left(1+2x\right)}{2CF\left(1,\frac{1}{2},x\right)+2\sqrt{x}{\text{e}}^x}\end{array}$

其中 $C=\frac{A}{B},B\ne 0$ 。

6. 结论

1) 本文以合流超几何方程为例，说明了弹性升阶变换可将某些一阶非线性常微分方程线性化，从而获得其解。

2) 从我们解决问题的思路中不难看出，只要通过弹性升阶变换后得到的方程可解，都可以采用该方法进行求解；显而易见，这种做法扩大了微分方程的可解类。

3) 弹性升阶变换求解非线性常微分方程的实质也是一种微分变换，但以往的微分变换只能对方程进行降阶求解，因此通过弹性升阶变换求解微分方程不仅克服了以往的方法不能升阶的困难，而且为微分方程的求解增加了一种新方法。