基于工质可压缩性的水泵水轮机驼峰初始工况导叶内部流动机理研究

Study on Internal Flow Mechanism of Pump-Turbine Guide Vane under Hump Initial Condition Considering Fluid Compressibility

摘要: 抽水蓄能系统在实现“双碳”目标方面具有重要意义，有利于与其他可再生资源相结合，形成环境友好型电力系统。水泵水轮机作为抽水蓄能系统的核心部件，驼峰区的形成会严重制约系统的安全性与稳定性，应予以考虑。此外，随着水泵水轮机向高扬程和大容量发展，工质的可压缩性变得不可忽略，不可压缩模型无法满足其高精度数值模拟研究的要求。针对这个问题，基于等温假设和Tait方程建立了一个弱压缩性模型，在这个模型的基础上对水泵水轮机内部的流场进行了数值模拟和分析。结果表明，考虑可压缩性计算出的驼峰曲线不仅与实验结果更加一致，而且还获得了更多的流动细节。对于近设计点的驼峰初始工况，虽然未考虑可压缩性和考虑后的结果皆表明导叶内部的流动结构引起的能量损失不容忽视，可压缩性对该流动结构发展还是比较显著的影响。

Abstract: Pumped hydrostorage systems take on a significance in fulfilling the “double carbon” goal, they are conducive to combined with other renewable resources to form environmental-friendly power sys-tems. The pump-turbine is the core component of the Pumped hydrostorage systems, in which the formation of hump region significantly restricts the safety and stability of the system that should be considered. Moreover, with the development of the pump-turbine to high head and large capacity, the compressibility of the working mass becomes non-negligible, and the incompressible model cannot meet the requirements of its high-precision numerical simulation study. For this problem, a weak compressibility model is built based on the isothermal assumption and Tait equation, the flow field inside the pump-turbine is simulated and analyzed base on this model. The results indicate that with considering the compressibility the calculated hump curve is not only more consistent with the experiment, but also it obtains more flow details. For the hump initial condition near the design point, although the results without and after considering compressibility show that the en-ergy loss caused by the flow structure inside the guide vanes cannot be ignored, compressibility still has a significant effect on the development of the flow structure.

1. 引言

“碳达峰”、“碳中和”大背景下，储能技术也迎来了新的发展。抽水蓄能技术作为目前储能市场上应用最广、占比最高的物理储能方式 [1] ，也迎来了新的技术挑战。为实现“双碳”目标，最近国家能源局发布《抽水蓄能中长期发展规划》 [2] 。可逆式水泵水轮机作为抽水蓄能电站的关键设备，在其以泵工况模式运行时，流量扬程曲线于小流量附近出现正斜率的驼峰区 [3] ，该现象主要是由其各过流部件内的不稳定流动引起。同时，驼峰出现也常伴随较大的震动和噪声，严重影响机组运行的安全性及稳定性 [4] [5] [6] [7] 。随着水泵水轮机朝着高扬程、大容量方向发展 [8] [9] ，其内部的流速和压力随之增大，此时管道中水的可压缩性会极大影响工质性质及内部流动。因此，在研究水泵水轮机驼峰特性的流动机理中考虑水的可压缩性都具有重要的意义。

导叶栅作为旋转机械中的主要部件，国内外研究学者对其内部流动机理与驼峰生成开展了大量的研究。Shibata等 [10] 等发现导致一多级泵流量扬程曲线驼峰区的主要原因是导叶能量损耗增加，且损耗增加是由于导叶区发生旋转失速。姚洋阳 [11] 结合模型试验进行多个流量工况点的非定常数值计算，结果表明随着流量减小，尾水管、叶轮及活动导叶的能量损失增加幅度过大导致性能曲线出现驼峰区。Li等 [12] 通过对水泵水轮机泵工况导叶压力脉动分析，导叶流道进口处的空化强度对低频压力脉动有显著影响，从而导致驼峰特性发生变化。

随着高扬程水泵水轮机研究的增多，原有的不可压缩计算模型无法满足计算要求。尽管可以用该模型计算并捕获到水泵水轮机内部的不稳定流动现象，但其对应频率下的压力幅值明显小于试验结果 [13] 。Trivedi等人 [14] 在一混流式水泵水轮机尾水管的压力脉动研究也发现类似现象。究其原因，此时水泵水轮机内部流场中的水流速和压力非常高，工质可压缩性对其性能及内部非定常流动的影响不可忽略 [9] [14] 。西安理工大学罗兴錡教授团队 [9] 、哈尔滨工业大学王洪杰教授团队 [15] 、Yan [16] 、Trivedi [14] 及Yang [13] 皆对可逆式水泵水轮的可压缩性进行研究，考虑水的可压缩性后，压力脉动的计算值更加接近试验值，但仍然偏小。

因此，在水泵水轮机内部流场高精度数值仿真研究中，相较于传统水力机械数值仿真所采用的不可压缩计算模型，计算中考虑工质可压缩性是十分必要的。综上所述，本文基于工质的可压缩性，建立对应弱可压缩计算模型并对水泵水轮机内部流场进行仿真，探究其驼峰初始工况下导叶栅内部的流动机理。

2. 数值模拟与分析方法

2.1. 水泵水轮机模型

本文研究对象为泵工况运行下的水泵水轮机，计算域沿流体进出口方向依次为尾水管、叶轮、活动导叶、固定导叶和蜗壳，其中叶轮包含9个后弯式扭曲叶片，导叶栅由20个固定导叶和20个活动导叶组成，几何模型如图1所示。模型的主要参数如下表1所示。

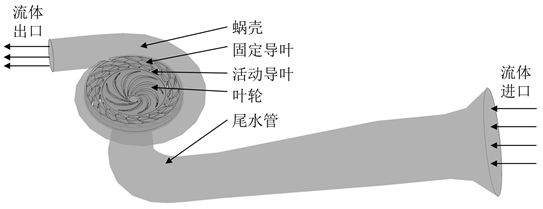
Figure 1. Pump-turbine geometric model

图1. 水泵水轮机几何模型

Table 1. Main parameters of the pump-turbine model

表1. 水泵水轮机模型主要参数

为了分析水泵水轮机的流场数据，本文对扬程H、频率f、流场特征量(速度v、压力p)作无量纲化处理得到对应的扬程系数 $\phi$ 、斯特劳哈尔数St、压力系数C_p和速度系数C_v：

$\phi =H/\left(u^2/2g\right)$ (1)

$St=\frac{f}{f_{\text{BPF}}}$ (2)

$C_p=\frac{p-\bar{p}}{\rho u^2/2}$ (3)

$C_v=\frac{v-\bar{v}}{v}$ (4)

式中，u为叶轮出口的圆周速度，单位为m/s；g为重力加速度，单位为m/s²；f_BPF为叶片通过频率，单位为Hz；p和 $\bar{p}$ 分别为瞬时压力和平均压力，单位为Pa； $\rho$ 为工质密度，单位为kg/m³；v和 $\bar{v}$ 分别为瞬时速度和平均速度，单位为m/s。其中水泵水轮机的叶片通过频率f_BPF和轴频f_R分别为150 Hz和16.67 Hz，对应的斯特劳哈尔数分别为St_BPF = 1和St_R ≈ 0.1111。

2.2. 数值计算

本文采用CFX对水泵水轮机内部流场进行数值模拟，流体域进口边界条件设置为质量流量，出口设置为平均静压，相对压力为0 Pa，壁面设置为无滑移边界条件，工质选取为水。时间步长为叶轮旋转1.5˚所需的时间0.00025 s，计算时长为1.8 s，采样频率为4000 Hz，频率误差为0.556 Hz，斯特劳哈尔数St误差为0.0037。定常计算使用SST k-ω模型，动静部件交界面选用Frozen Rotor模型。非定常计算湍流模型采用分离涡(DES)模型，动静部件交界面选用Transient Rotor Stator模型，非定常计算以定常计算结果作为初值。

采用ICEM对计算域进行六面体结构化网格划分，并加密壁面边界层网格。将设计流量工况下未考虑水可压缩性的扬程系数作为参照值，共划分三套网格进行网格无关性验证，网格数分别为619万、892万、1259万，验证结果如表2所示。结果表明扬程系数与试验值的相对误差均小于4%，1259万网格数的扬程系数相比两套低密度网格更接近于试验值，相对误差约为3.3%，综合网格数及计算资源，最终选用网格数为1259万的结构化网格进行后续数值计算，该套网格的各过流部件具体网格数如表3所示。

Table 2. Gridindependence analysis

表2. 网格无关性分析

Table 3. Grid number of the respective flow passage component of the pump-turbine

表3. 水泵水轮机各过流部件网格数

2.3. 监测点与监测面

为了分析导叶栅内部流场及流场特征量，沿轮毂到前盖板方向依次建立三个径向截面，如图2所示。采用无量纲距离Span值描述径向截面位置，定义为径向截面至轮毂距离与轮毂至前盖板距离的比值，其中Span = 0表示轮毂，Span = 1表示前盖板，三个径向截面沿轮毂至前盖板方向依次为Span = 0.1、Span = 0.5、Span = 0.9。在导叶栅进口设置两个监测点GV1和GV2，如图3所示。

Figure 2. Location of the radial section of the guide vane cascade

图2. 导叶栅径向截面位置图

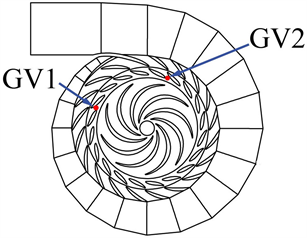
Figure 3. Distribution of monitoring points for the guide vane cascade

图3. 导叶栅监测点分布图

2.4. 弱可压缩模型

本研究中，在进行可压缩数值模拟时，密度的变化率相对N-S其他项而言较小，将方程中密度变化

项 $\frac{\partial \rho }{\partial t}$ 设为0，即弱可压缩。水泵水轮机工作环境温度变化也小，因此在计算中假设其运行温度为恒定值。

在等温假设下，基于液体物性Tait方程表征水的弱可压缩性，将水密度与压力和温度的函数简化为与压力的函数：

$\rho ={\rho }_0\times {\left(1+\frac{n\left(p-p_0\right)}{k_0}\right)}^{\frac{1}{n}}$ (5)

式中，p和p₀分别表示水的绝对压力和25℃水的参考压力； $\rho$ 和 ${\rho }_0$ 分别表示水在绝对压力p和参考压力p₀下的密度；n为密度指数，值为7.15；k₀为参考压力p₀下的体积模量，值为2.2×10⁹ Pa。

将函数(5)加入到数值计算中，实现数值模拟过程中反映水密度变化的目标，进而体现水泵水轮机运行中水的弱可压缩性。

3. 试验验证

将水泵水轮机不同流量工况下数值计算得到的扬程系数与实验测量得到的扬程系数对比，对比结果如图4所示，相对误差如表4所示，相对误差γ公式如下：

$\begin{array}{l}{\gamma }_{\text{com}}=\frac{\left|{\phi }_{\exp }-{\phi }_{\text{com}}\right|}{{\phi }_{\exp }}\times 100\text{\%}\\ {\gamma }_{\text{incom}}=\frac{\left|{\phi }_{\exp }-{\phi }_{incom}\right|}{{\phi }_{\exp }}\times 100\text{\%}\end{array}$ (6)

式中，j_exp为试验扬程系数，j_com为可压缩数值模拟扬程系数，j_incom为不可压缩数值模拟扬程系数；γ_com为可压缩相对误差，γ_incom为不可压缩相对误差，以百分比表示。

从图4和表4中可以看出，数值模拟可以很好的预测水泵水轮机泵工况的驼峰现象，数值模拟中考虑可压缩性后得到的扬程系数更加接近于实验值，相对误差相较于未考虑可压缩性更小，误差大小皆小于2%。

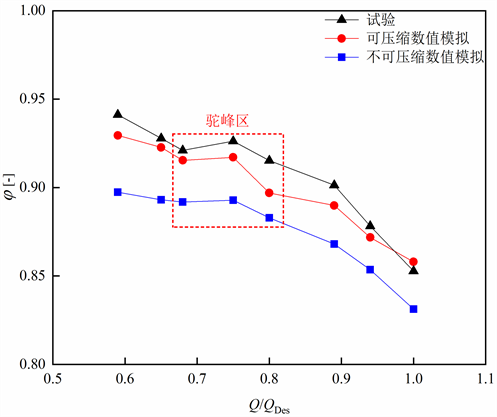
Figure 4. Comparison of the numerical simulation and experimental head coefficient

图4. 数值模拟与试验扬程系数对比

Table 4. Relative error of the head coefficient

表4. 扬程系数相对误差

将试验和数值模拟采取的压力数据作快速傅里叶变换得到压力脉动频谱进行对比分析。以驼峰区工况0.75Q_Des的导叶栅进口监测点GV1的压力脉动频谱为例，如图5所示，发现可压缩数值模拟的特征频率St_0.0111及叶片通过频率St_BPF的压力脉动幅值相对于不可压缩数值模拟更加接近于试验值，进一步验证了数值模拟计算加入可压缩性的必要性。

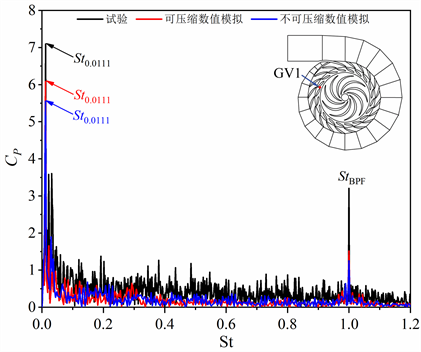
Figure 5. Pressure fluctuation spectrum of the guide vane cascade monitoring point GV1 under 0.75Q_Des

图5. 0.75Q_Des导叶栅监测点GV1的压力脉动频谱

4. 计算结果与分析

4.1. 水力损失分析

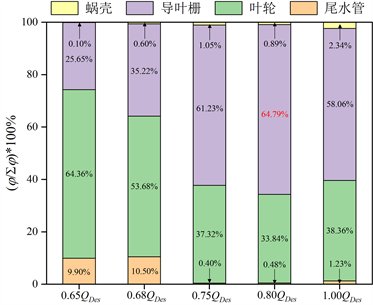
图6对比了考虑和未考虑工质可压缩性结果的各过流部件的水力损失相应占比。由图4可知该水泵水轮机的驼峰区主要起始于0.8Q_Des附近，对比该工况结果发现，在未考虑可压缩性时，导叶的能量损失占比高达64.79%，在各部件的能量损失中占主导作用。该结论也与之前驼峰区相关的研究结果相吻合：导叶是水泵水轮机泵工况近设计点驼峰的主要过流部件 [17] 。在考虑可压缩性后，除了0.8Q_Des，其它工况虽然能量损失占比数值上有些变化，但是各过流部件的能量损失变化趋势都比较相似。

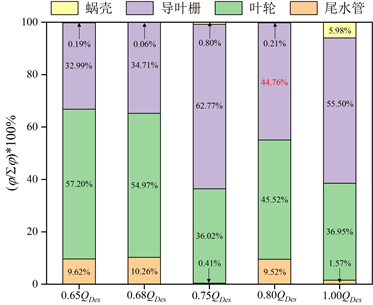(a) (b)

Figure 6. Comparison of hydraulic losses of the respective flow component with compressible and incompressible results under different flow conditions. (a) Incompressible; (b) Compressible

图6. 不同流量工况下可压缩及不可压缩结果的各过流部件水力损失对比图。(a) 不可压缩；(b) 可压缩

因此本文主要分析0.8Q_Des下导叶栅内部流动的变化机理，探索工质可压缩性对其内部流动的影响及与驼峰之间的关系。当流量处于0.8Q_Des时，考虑可压缩性后的计算结果中导叶栅能量损失占比明显下降，占到所有过流部件总能量损失的44.76%，此时对应叶轮能量损失占比为45.52%，略大于导叶的能量损失，但两者在总能量损失中的占比不容忽视。同时，可压缩计算结果更加接近实验值，所以进一步推断导叶栅内部的流动能量损失不容忽视，是引起性能曲线驼峰的一个主要因素。

4.2. 内部流场分析

0.8Q_Des不可压缩与可压缩的导叶栅不同Span值径向截面的流线分布对比如图7所示。不可压缩导叶栅轮毂附近导叶栅流道出现三个明显的堵塞区，堵塞区是由导叶栅进口的三个高速区和三个低速区引起，该区域沿轮毂向前盖板方向逐渐减弱。在加入可压缩模型后，导叶栅内部流场同样于轮毂附近出现三个堵塞区，但堵塞区域大幅度减小，该区域由轮毂向前盖板逐渐增大。因此推断0.8Q_Des可压缩导叶栅水力损失大幅度降低的主要原因可能是导叶栅流道堵塞现象的变化。

(a) 不可压缩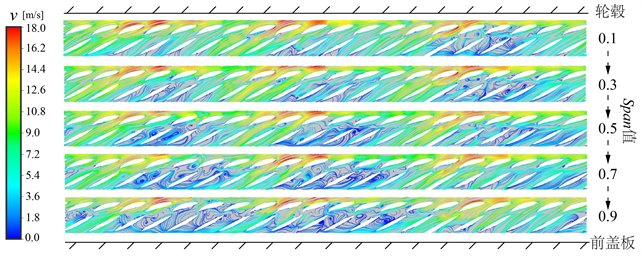(b) 可压缩

Figure 7. Comparison of streamlines in different Span sections of the guide vane cascade under 0.8Q_Des

图7. 0.8Q_Des导叶栅不同Span截面流线对比图

4.3. 频谱分析

对0.8Q_Des不可压缩与可压缩结果的导叶栅流道监测点的速度脉动作快速傅里叶变换，得到的速度频谱结果如图8所示。未考虑工质可压缩性的速度频域特征表明最显著的峰值出现在频率St ≈ 0.0074 (St_0.0074)附近。考虑可压缩性后的结果表明，峰值依旧出现在频率St ≈ 0.0074 (St_0.0074)附近，但此时该频率对应的速度频谱幅值明显下降，可能是可压缩导叶栅水力损失降低的主要原因。

因此推测：无论是否考虑可压缩性，驼峰初始流量0.8Q_Des的导叶栅内部主要非定常流动结构的特征频率皆为St_0.0074，但是流动结构的作用大小有所改变。

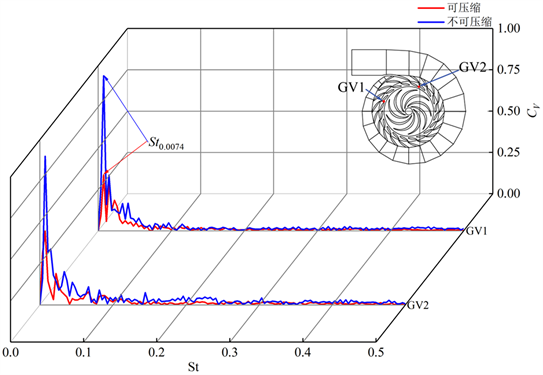
Figure 8. Comparison of velocity pulsation spectrum at monitoring points of the guide vane cascade under 0.8Q_Des

图8. 0.8Q_Des导叶栅流道监测点速度脉动频谱对比图

4.4. 二维时频域分析

为了进一步验证特征频率St_0.0074的流动结构空间分布，对0.8Q_Des下导叶栅不同Span截面特征频率的速度脉动幅值二维分布进行分析，其结果如图9所示。在未考虑工质可压缩性时，导叶栅在频率St_0.0074下的高幅值主要集中在固定导叶前缘及活动导叶流道，且在轮毂处最显著；而朝前盖板方向，速度脉动幅值区域变弱，分布于固定导叶进口。与图7(a)流线图中的堵塞区域结构特点吻合。但考虑可压缩性后计算出的流场，导叶栅的堵塞区明显减弱，见图7(b)，速度脉动高幅值区域变化规律与不可压缩相反，在轮毂附近高幅值区分布在固定导叶尾缘，前盖板附近则分布在整个导叶栅流道。因此推断在考虑工质可压缩性后，0.8Q_Des导叶栅水力损失减小主要是因为导叶栅特征频率对应的高脉动幅值区域变小，内部非定常流动结构发生变化。

(a) 不可压缩(b) 可压缩

Figure 9. Comparison of 2D distribution of velocity pulsation amplitude of frequency St_0.0074 in 0.8Q_Des guide vane cascade

图9. 0.8Q_Des导叶栅中频率St_0.0074的速度脉动幅值二维分布对比图

5. 结论

综上所述，在水泵水轮机驼峰区流场的数值仿真中，考虑工质可压缩性的计算可以抓住更多的流动细节，同时其结果更加接近于实验值。本文基于所建立的弱可压缩模型，从能量、空间分布及频域特征三方面研究水泵水轮机驼峰初始时导叶栅内部的流动机理，并得到以下结论：

1) 在驼峰初始工况0.8Q_Des，相较于未考虑工质可压缩性的结果显示导叶栅是该工况主要能量损失部件，考虑可压缩性结果进一步说明导叶栅内部的流动能量损失不容忽视，是引起性能曲线驼峰的一个主要因素。

2) 当不考虑可压缩性，0.8Q_Des导叶栅中主要的非定常流动结构是特征频率为St_0.0074的堵塞区，发生在固定导叶前缘及活动导叶流道，堵塞区沿轮毂向前盖板方向逐渐减弱。

3) 考虑可压缩性的结果表明：当流量处于0.8Q_Des时，导叶栅流道仍然存在特征频率均为St_0.0074的流动结构。但堵塞区域减小，堵塞区分布规律与未考虑可压缩性时相反，沿轮毂向前盖板方向逐渐增强。

以上流动结构的存在使得导叶栅内部的水头损失降低，是水泵水轮机在该工况出现驼峰区的主要原因之一。

基金项目

国家自然科学基金资助项目(51976125)。

参考文献

NOTES

^*通讯作者。