关于具有不可分离哈密顿量的平均场控制系统的策略迭代算法的研究

A Study on the Policy Iteration Method for Time-Dependent Mean Field Controls Systems with Non-Separable Hamiltonians

摘要: 平均场控制研究的是在大量智能体参与的系统中，由一个中心控制者计算系统的帕累托最优，且所有个体先验地使用完全相同的反馈控制。本文研究的对象是一类来自于平均场控制问题的倒向–正向偏微分方程组有限差分数值计算方法，使用的算法基于最优控制问题中的策略迭代方法。本文讨论了较短时间区域内算法的收敛性和收敛速度。本文通过一些例子验证了算法的有效性。本文通过数值试验讨论了平均场博弈纳什均衡和平均场控制帕累托最优之间的总体效益比较。

Abstract: Mean field type control studies the Pareto optimum computed by a central planner in a system with large number of agents, with each agent using a priori the same feedback control. This paper stud-ies the finite difference numerical approximation of a type of Mean field type control problem, using algorithms based on the policy iteration method from optimal control problems. Under the as-sumption of a short time horizon, convergence of the algorithm and the rate of convergence are discussed. Some numerical examples are supplemented to show the efficacy of the algorithms. The comparisons between Nash equilibrium and Pareto optimum, in terms of aggregate utility, are il-lustrated by numerical examples.

1. 引言

近年来，随着人工智能技术的发展，面对日益复杂的系统控制和决策问题，人们研究大规模多智能体系统的平均行为和博弈策略，提出平均场博弈模型(Mean Field Game，简称MFG)和平均场控制系统 (Mean Field Control，简称MFC)来指导个体的决策和行动，从而实现系统整体的优化和协同。为了比较效率，定义“Price of Anarchy”(简称POA)为纳什均衡下全局效用与最优全局效用之间的比率。

自2006年Lasry和Lions [1] 、Huang等 [2] 首次提出平均场博弈的数学PDE模型以来，MFG与MFC广泛应用于交通拥堵、能源市场、金融市场等领域 [1] 。Achdou等 [3] 从PDE的角度对平均场控制系统进行理论研究，给出了一些例子的PDE的存在性和唯一性结果，并通过简单的数值模拟比较了MFG和MFC。Carmona等 [4] 从概率的角度研究了MFC的解的性质，并证明了对应PDE的解是MFG的近似纳什均衡。Bensoussan等 [5] 全面介绍并比较了MFG与MFC问题。文献 [6] [7] 介绍了平均场博弈系统的有限差分等数值解法，提出了前向–后向系统的数值格式，并对其数值效果进行了验证。Cacace等 [8] 对有可分哈密顿量的MFG引入了的策略迭代算法。Camilli等 [9] 提到了分析了MFG中策略迭代算法的收敛条件和收敛速度的估计。Cardaliaguet等 [10] 介绍了MFG系统中POA的意义，并深入探讨了POA的计算和优化问题。Carmona等 [11] 分析了对于社会最优成本而言MFC与MFG的区别，并讨论了影响POA的参数。

数值解对理论研究和实际问题很重要。但是目前的很多数值解法只适用在可分离哈密顿量的条件下，而对MFC的理论研究大部分针对的是非局部依赖的条件。策略迭代算法是最优控制问题中常见的求解的方法，已经成功应用于MFG问题中。但是将策略迭代算法扩展到不可分离哈密顿量的平均场控制问题目前尚缺乏研究。本论文的主要目标是提出一种策略迭代算法来解决非可分离哈密顿量的MFC问题。在一定的假设下，我们证明算法收敛于最优策略。我们使用该算法计算POA，讨论了MFC问题中几类参数对POA的影响。

2. 主要内容

2.1. MFG与MFC

平均场博弈问题通常由以下方程组描述：

$\{\begin{array}{l}-{\partial }_{t}u-\nu \Delta u+H\left(m,Du\right)=f\left(x,m\right)\hfill \\ {\partial }_{t}m-\nu \Delta m-\mathrm{div}\left(m{H}_p\left(m,Du\right)\right)=0\hfill \\ m\left(x,0\right)=m_0\left(x\right),u\left(x,T\right)=u_T\left(x\right)\hfill \end{array}$ (1)

平均场型控制问题与MFG的不同之处在于，虽然没有智能体能够单独偏离其策略以最大化其个人利益，但有一个监督者要让群体合作使得共同利益最大化。所以，我们不能假设我们知道平均状态的密度分布，然后得到与该平均值对应的最优控制，因为这里平均值取决于监督者设置的控制。我们参考Graber [12] 文章中第5节，用最优控制问题的帕累托最优来刻画MFC系统的PDE。

平均场类型的控制问题(MFC)通常由以下方程组描述：

$\{\begin{array}{l}-{\partial }_{t}u-\nu \Delta u+Du\cdot q-L\left(m,q\right)-m{L}_m\left(m,q\right)=0\hfill \\ {\partial }_{t}m-\nu \Delta m-\mathrm{div}\left(m{H}_p\left(m,Du\right)\right)=0\hfill \\ m\left(x,0\right)=m_0\left(x\right),u\left(x,T\right)=u_T\left(x\right)\hfill \end{array}$ (2)

虽然MFC与MFG的可以用类似的PDE刻画最优解，但是MFC中u不代表个体的价值函数，它的方程只是有类似于HJB方程的结构，所以可以利用HJB相关的数学方法来解决。

2.2. 算法

首先我们对后文出现的哈密顿量 $H\left(m,p\right)$ 做出假设：

(H1) H关于p，m是连续的。H， $H_{p_i}$ ， $H_{p_i{p}_j}$ ， $H_{m{p}_i}$ 是关于 $\left(p,m\right)\in {ℝ}^d\times {ℝ}^{+}$ 的局部Lipschitz连续函

数。 $H\left(m,p\right)=\frac{{\left|p\right|}^{\gamma }}{{\left(c+m\right)}^{\beta }}+f(\; m\; )$

(H2) H关于变量p是严格凸的。

比如哈密顿量 $H\left(m,p\right)$ 的形式如下：

$H\left(m,p\right)=\frac{{\left|p\right|}^{\gamma }}{{\left(c+m\right)}^{\beta }}+f(\; m\; )$

注意到当 $q^{*}=H_p\left(m,Du\right)$ 时，

$H_m\left(m,Du\right)=-L_m\left(m,q^{*}\right)$ (3)

因为从Cirant等 [13] 的工作中已知解在 $W_r^{2,1}\left(Q\right)$ 空间中的存在唯一性，故存在某一个足够大的R使得 $q=H_p\left(m,p\right)$ 成立。基于对之前的文献的研究总结，我们针MFC系统提出了以下两种策略迭代算法：策略迭代算法包括迭代更新密度分布函数、价值函数和控制函数。在算法中首先引入控制函数的一个上界 $R>0$ ， $Q:={\mathbb{T}}^d\times \left[0,T\right]$ ， ${\mathbb{T}}^d$ 代表环 ${ℝ}^d/{\mathbb{Z}}^d$ 。假设有界可测的向量场 $q^{\left(0\right)}:{\mathbb{T}}^d\times \left[0,T\right]\to {ℝ}^d$ 满足 $\left|q^{\left(0\right)}\right|\le R$ ，

${\Vert \mathrm{div}{q}^{\left(0\right)}\Vert }_{L^r\left(Q\right)}\le R$ 。

Algorithm 1：具有不可分离哈密顿量的平均场控制系统的策略迭代算法(PI1)

Data:由初始的 $q^{\left(n\right)}$ ，求出密度分布 $m^{\left(n\right)}$ 和 $u^{\left(n\right)}$ 后，更新策略 $q^{\left(n+1\right)}$ ，再迭代。

[1] for $n=0,1,2,\cdots ,N$ do

[2]计算 $m^{\left(n\right)}$ ；

$\{\begin{array}{ll}{\partial }_t{m}^{\left(n\right)}-\nu \Delta m^{\left(n\right)}-\mathrm{div}\left(m^{\left(n\right)}{q}^{\left(n\right)}\right)=0,\hfill & \text{in}Q\hfill \\ m^{\left(n\right)}\left(x,0\right)=m_0\left(x\right)\hfill & \text{in}{\mathbb{T}}^d\hfill \end{array}$ (4)

[3]计算 $u^{\left(n\right)}$ ；

$\{\begin{array}{ll}-{\partial }_t{u}^{\left(n\right)}-\nu \Delta u^{\left(n\right)}-\mathcal{L}\left(m^{\left(n\right)},D{u}^{\left(n-1\right)},q^{\left(n\right)}\right)\hfill & \hfill \\ +q^{\left(n\right)}D{u}^{\left(n\right)}-m{\mathcal{L}}_m\left(m^{\left(n\right)},D{u}^{\left(n-1\right)},q^{\left(n\right)}\right)=0\hfill & \text{in}Q\hfill \\ u^{\left(n\right)}\left(x,T\right)=u_T\left(x\right)\hfill & \text{in}{\mathbb{T}}^d\hfill \end{array}$ (5)

$\mathcal{L}\left(m,p,q\right)=p\cdot q-H\left(m,p\right)$ (6)

[4]更新策略 $q^{\left(n+1\right)}$

$q^{\left(n+1\right)}\left(x,t\right)=\arg {\max }_{\left|q\right|\le R}\left\{q\cdot D{u}^{\left(n\right)}\left(x,t\right)-L\left(m^{\left(n\right)},q\right)\right\}\text{in}Q$

判断是否停止迭代；若否，则返回策略评估。

[5] end

我们注意到不可分离哈密顿量带来的一个核心变化是， $q=H_p\left(m,Du\right)$ 显性地依赖于m。对于可分离的形式 $q=H_p\left(Du\right)$ ，控制对m的依赖是非显性的，通过价值函数u对m体现。我们可以设计一个新的算法，在概率密度和价值函数的每次更新之间更新控制q。

Algorithm 2：具有不可分离哈密顿量的平均场控制系统的策略迭代算法(PI2)

Data:由初始的 $q^{\left(n\right)}$ ，求出密度分布 $m^{\left(n\right)}$ 和 $u^{\left(n\right)}$ 后，更新策略 $q^{\left(n+1\right)}$ ，再迭代。

[1] for $n=0,1,2,\cdots ,N$

[2]计算 $m^{\left(n\right)}$ ；

$\{\begin{array}{ll}{\partial }_t{m}^{\left(n\right)}-\nu \Delta m^{\left(n\right)}-\mathrm{div}\left(m^{\left(n\right)}{q}^{\left(n\right)}\right)=0,\hfill & \text{in}Q\hfill \\ m^{\left(n\right)}\left(x,0\right)=m_0\left(x\right)\hfill & \text{in}{\mathbb{T}}^d\hfill \end{array}$ (7)

[3]更新策略 ${\tilde{q}}^{\left(n\right)}$ ；

${\tilde{q}}^{\left(n\right)}\left(x,t\right)=\arg {\max }_{\left|q\right|\le R}\left\{\tilde{q}\cdot D{\tilde{u}}^{\left(n-1\right)}\left(x,t\right)-L\left(m^{\left(n\right)},\tilde{q}\right)\right\}\text{in}Q$ (8)

[4]计算 $u^{\left(n\right)}$ ；

$\{\begin{array}{ll}-{\partial }_t{\tilde{u}}^{\left(n\right)}-\nu \Delta {\tilde{u}}^{\left(n\right)}+{\tilde{q}}^{\left(n\right)}D{\tilde{u}}^{\left(n\right)}-L\left(m^{\left(n\right)},{\tilde{q}}^{\left(n\right)}\right)\hfill & \hfill \\ -m{L}_m\left(m^{\left(n\right)},{\tilde{q}}^{\left(n\right)}\right)=0\hfill & \text{in}Q\hfill \\ {\tilde{u}}^{\left(n\right)}\left(x,T\right)=u_T\left(x\right)\hfill & \text{in}{\mathbb{T}}^d\hfill \end{array}$ (9)

[5]再次更新策略 $q^{\left(n+1\right)}$ ；

$q^{\left(n+1\right)}\left(x,t\right)=\arg {\max }_{\left|q\right|\le R}\left\{q\cdot D{\tilde{u}}^{\left(n\right)}\left(x,t\right)-L\left(m^{\left(n\right)},q\right)\right\}\text{in}Q$ (10)

判断是否停止迭代；若否，则返回策略评估。

[6] end

显然，当H是可分形式的哈密顿量时，则算法(PI1)与(PI2)是等价的。虽然出现在(9)和(10)的L是拉格朗日量，但定义并出现在(6)和(5)的项 $\mathcal{L}$ 只是近似的拉格朗日量。它不是由勒让德变换得到。但是如果算法收敛，即 $D{u}^{\left(n-1\right)}\to D{u}^{*}$ ， $q^{\left(n\right)}\to q^{*}$ ， $m^{\left(n\right)}\to m^{*}$ 且 $q^{*}=H_p\left(m,Du\right)$ 则 $\mathcal{L}\left(m^{\left(n\right)},D{u}^{\left(n-1\right)},q^{\left(n\right)}\right)\to L\left(m^{*},q^{*}\right)$ 。在(PI1)代码中，实际上不会用到 $D{u}^{\left(n-1\right)}$ ， $\mathcal{L}$ 的意义只是为了在理论上，完全从H的性质出发。

2.3. 收敛性分析

除了上一节对H做出的假设(H1)，(H2)外，我们增加以下假设。

(I1) 当有 $r>d+2$ ， $m_0\in W_r^2\left({\mathbb{T}}^d\right)$ ， $m_0\ge \underset{\_}{m}>0$ 和 ${\displaystyle {\int }_{{\mathbb{T}}^d}{m}_0}\left(x\right)\text{d}x=1$ 时 $u_T\in W_{\infty }^2(\; T\; d\; )$

我们定义以下空间。

$X_M^T=\left\{\left(u,m\right):u\in C^{1,0}\left(Q\right)\cap W_r^{2,1}\left(Q\right),m\in C^{1,0}\left(Q\right){\Vert u\Vert }_{W_r^{2,1}\left(Q\right)}+{\left|u\right|}_Q^{\left(1\right)}+{\left|m\right|}_Q^{\left(1\right)}\le M\}+{\left|u\right|}_Q^{\left(1\right)}+{\left|m\right|}_Q^{\left(1\right)}\le M\right\}$ (11)

用 $\mathcal{T}\left(u,m\right)=\left(\hat{u},\hat{m}\right)$ 定义 $X_M^T$ 上的算子 $\mathcal{T}$ ，满足：

$\{\begin{array}{l}{\partial }_t\hat{m}-ϵ\Delta \hat{m}-H_p\left(m,Du\right)D\hat{m}-H_{pm}\left(m,Du\right)\left(Dm\right)\hat{m}-{\displaystyle \underset{i,j}{\sum }{H}_{p_j{p}_i}}\left(m,Du\right)\left({\partial }_{x_j{x}_i}^{2}u\right)\hat{m}=0\\ -{\partial }_t\hat{u}-ϵ\Delta \hat{u}+H_p\left(m,Du\right)D\hat{u}-\mathcal{L}\left(\hat{m},Du,H_p\left(m,Du\right)\right)-\hat{m}{\mathcal{L}}_m\left(\hat{m},Du,H_p\left(m,Du\right)\right)=0\\ \hat{u}\left(x,T\right)={\hat{u}}_T\left(x\right),\hat{m}\left(x,0\right)={\hat{m}}_0\left(x\right)\end{array}$ (12)

定理2.1. 假设之前的(H1)，(H2)和(I1)仍成立，取K满足

$K\ge \max \left\{\frac{2}{\underset{\_}{m}},2{\left|m_0\right|}_{{\mathbb{T}}^d}^{\left(1\right)},2{\left|u\left(\cdot ,T\right)\right|}_{{\mathbb{T}}^d}^{\left(1\right)}\right\}$ (13)

设

$M_1=2\left({\left|m_0\right|}_{{\mathbb{T}}^d}^{\left(1\right)}+{\left|u_T\right|}_{{\mathbb{T}}^d}^{\left(1\right)}\right)$ (14)

则存在足够小的 $\bar{T}$ 满足对任意的 $T\in \left(0,\bar{T}\right]$ ，映射 $\mathcal{T}$ 是空间

$X_{M_1}^T\cap \left\{\left(u,m\right):{\left|u\right|}_Q^{\left(1\right)}\le K,1/K\le m\le K\right\}$

中的压缩映射算子。

定理2.2. 假设之前的(H1)，(H2)和(I1)仍成立，则存在足够小的 $\bar{T}$ 满足对任意的 $T\in \left(0,\bar{T}\right]$ ，MFC系统(1.2)有唯一的解 $\left(u^{*},m^{*}\right)\in W_r^{2,1}\left(Q\right)\times W_r^{2,1}\left(Q\right)$ 。

定理2.3. 假设之前的(H1)，(H2)和(I1)仍成立，根据定理1.2.1取 $\bar{T}$ 。则存在一个 ${\hat{T}}_1\le \bar{T}$ 满足对任意的 $T\in \left(0,{\hat{T}}_1\right]$ 和R足够大时，由策略迭代算法(PI1)生成的解序列 $\left(u^{\left(n\right)},m^{\left(n\right)}\right)$ ，收敛到(1.2)的解 $\left(u^{*},m^{*}\right)\in W_r^{2,1}\left(Q\right)\times W_r^{2,1}\left(Q\right)$ 。

定理2.1，定理2.2，定理2.3分别对应Lauriere，Song与Tang [13] 中的定理3.1，3.2和3.3，我们在此省略证明，本质区别在于关于 $\hat{u}$ 的方程中所出现的

$-\hat{m}{\mathcal{L}}_m\left(\hat{m},Du,H_p\left(m,Du\right)\right)$

基于假设(H1)，(H2)和(I1)不难得到与这一项相关的估计。由于篇幅限制，我们在此省略算法 (PI2) 收敛性分析与收敛速度的证明细节。

2.4. 收敛速度分析

本节中的定理和推论完全类似于Lauriere，Song与Tang [13] 中第4节关于平均场博弈系统的结果。我们给出相应的结论，具体的证明细节我们会在后续的工作中给出。特别地，我们用 $\left(u^{*},m^{*}\right)$ 和 $q^{*}$ 分别

表示方程组(1.1)的解和对应问题的最优控制。我们证明在T较小的假设前提下，误差 ${\Vert u^{\left(n+1\right)}-u^{*}\Vert }_{W_r^{2,1}\left(Q\right)}$ 和 ${\Vert m^{\left(n+1\right)}-m^{*}\Vert }_{W_r^{2,1}\left(Q\right)}$ 具有线性收敛速度。

定理2.4. 假设(H1)，(H2)和(I1)有效，取和定理2.3一样的 ${\hat{T}}_1$ 和R。则存在一个对于所有 $T\in \left(0,{\hat{T}}_1\right]$ 有界的常数C，它仅取决于问题的数据。此时，由策略迭代方法(PI1)生成的序列 $\left(u^{\left(n\right)},m^{\left(n\right)}\right)$ 满足下列不等式：

${\Vert m^{\left(n+1\right)}-m^{*}\Vert }_{W_r^{2,1}\left(Q\right)}\le C\left({\Vert q^{\left(n+1\right)}-q^{*}\Vert }_{L^r\left(Q\right)}+{\Vert \mathrm{div}\left(q^{\left(n+1\right)}-q^{*}\right)\Vert }_{L^r\left(Q\right)}\right)$ (15)

和

${\Vert u^{\left(n+1\right)}-u^{*}\Vert }_{W_r^{2,1}\left(Q\right)}\le C{T}^{\frac{1}{2}-\frac{d}{2r}}\left({\Vert u^{\left(n\right)}-u^{*}\Vert }_{W_r^{2,1}\left(Q\right)}+{\Vert m^{\left(n+1\right)}-m^{*}\Vert }_{W_r^{2,1}\left(Q\right)}\right)$ (16)

推论2.5. 设 $M^{\left(n\right)}=m^{\left(n\right)}-m^{*}$ ， $U^{\left(n\right)}=u^{\left(n\right)}-u^{*}$ 对所有 $n\ge 0$ 成立。与定理2.4相同的假设下，下列估计对 $n\ge 1$ 都成立：

${\Vert U^{\left(n+1\right)}\Vert }_{W_r^{2,1}\left(Q\right)}+{\Vert M^{\left(n+1\right)}\Vert }_{W_r^{2,1}\left(Q\right)}\le C{T}^{\frac{1}{2}-\frac{d}{2r}}\left({\Vert U^{\left(n\right)}\Vert }_{W_r^{2,1}\left(Q\right)}+{\Vert M^{\left(n\right)}\Vert }_{W_r^{2,1}\left(Q\right)}+{\Vert U^{\left(n-1\right)}\Vert }_{W_r^{2,1}\left(Q\right)}\right)$ (17)

进而存在 $\mathcal{l}>1$ ，足够大的 $n_0$ 和足够小的 $\stackrel{⌣}{T}\in \left(0,{\hat{T}}_1\right]$ 满足对任意 $T\in \left(0,\stackrel{⌣}{T}\right]$ ，我们都有线性收敛速度，即，

${\Vert U^{\left(n\right)}\Vert }_{W_r^{2,1}\left(Q\right)}+{\Vert M^{\left(n\right)}\Vert }_{W_r^{2,1}\left(Q\right)}\le {\left(\frac{1}{\mathcal{l}}\right)}^{n-n_0}\left({\Vert U^{\left(n_0\right)}\Vert }_{W_r^{2,1}\left(Q\right)}+{\Vert M^{\left(n_0\right)}\Vert }_{W_r^{2,1}(\; Q\; )}\right)$

3. 实验

我们在Lauriere等人的 [14] 工作基础上对基于MFG的策略迭代算法做出了新的改进，对MFC系统引入了新的策略迭代方法(PI1)和(PI2)。并对MFC系统使用有限差分方法，给出具体的数值实验例子和分析。对于数值实验的图像与说明，本文比较同一最优控制问题的MFC和MFG的策略迭代方法计算的数值结果差异。类似于Carmona等 [11] ，关注计算MFG与MFC中的POA。据我们所知，目前还没有人用策略迭代算法计算在MFC中，具有局部依赖条件下的POA。

3.1. 算法实现

我们先给出该平均场控制系统中对应的函数参数形式，然后在具体数值实验中再赋予相关参数值。拉格朗日量是：

$L\left(m,q\right)=\frac{1}{2}r{\left(1+m\right)}^{\beta }{\left|q\right|}^2+f(\; m\; )$

其中 $f\left(m\right)=\zeta m+\gamma \left(1-{\text{e}}^{-10{\left(x-0.25\right)}^2}\right)$ ，则：

$L_m\left(m,q\right)=\frac{1}{2}r\beta {\left(1+m\right)}^{\beta -1}{\left|q\right|}^2+\zeta$

哈密顿量是：

$\begin{array}{c}H\left(m,Du\right)=\underset{q\in {ℝ}^d}{\sup }\left\{q\cdot Du-\frac{1}{2}r{\left(1+m\right)}^{\beta }{\left|q\right|}^2-f\left(m\right)\right\}\\ =\frac{1}{2r{\left(1+m\right)}^{\beta }}{\left|Du\right|}^2-f(\; m\; )\end{array}$

其中 $\beta$ ， $\zeta$ 为正常数。最后的常数 $\zeta$ 是人群厌恶成本，表示智能体不愿意处于非常拥挤的区域。

在计算时MFG求解纳什均衡，MFC求解帕累托最优问题，分别用 $J_{mfc}$ 和 $J_{mfg}$ 表示两类不同的社会总成本：

$\{\begin{array}{l}{J}_{mfg}=J\left(q;m\right)=\mathbb{E}\left[{\displaystyle {\int }_0^{T}L}\left(m,q\right)\text{d}s+g\left(X_T,m\left(T\right)\right)\right]\hfill \\ J_{mfc}={\displaystyle {\int }_0^T{\displaystyle {\int }_{{\mathbb{T}}^d}L}}\left(m,q\right)m\text{d}s\text{d}x+{\displaystyle {\int }_{{\mathbb{T}}^d}g}\left(x,m\left(T\right)\right)m^q\text{d}x\hfill \end{array}$ (18)

但是在实际计算过程中，因为我们是对m的局部依赖，所以用 $g\left(X_T\right)$ 代替 $g\left(X_T,m\left(T\right)\right)$ 计算。接着我们给出对于大规模多智能体系统控制问题的POA的数学计算表达式：

$\text{POA}=\frac{J_{mfc}}{J_{mfg}}$

理论上POA应该大于1，我们通过多组同参数下的数值实验验证此结论。为了研究比较MFG与MFC系统中运行成本、群体密度分布和终止条件对计算POA的影响，找到优化大规模多智能体系统的控制问题中的社会总成本的方法，我们把对应函数都参数化。

我们在 ${\mathbb{T}}^d$ 上固定一个网格 $\mathcal{G}$ 。然后，我们用U、M和Q表示 $\mathcal{G}$ 上的矢量，分别逼近 MFC 的解和控制策略。这里我们使用均匀网格和中心二阶有限差分来计算离散的拉普拉斯算子。而对于时间的离散化，我们采用隐式欧拉方法来处理时间前向的KFP方程和时间后向的HJB方程。在具体实施过程中我们在空间上使用了I = 200的节点数，在时间上使用了N = 200的节点数。把初始控制策略设定为：在 $\mathcal{G}$ 上对所有 $Q_n^{\left(0\right)}\equiv \left(0,0\right)$

我们给出下面的一维实例。让所有智能体在规定时间内向某个目标移动，并根据在时间结束时智能体与目标位置的距离来惩罚智能体。智能体的状态范围是一维环形 $\mathbb{T}=ℝ/\mathbb{Z}$ 。假设移动的目标位于0.8处。我们取初始的群体分布 $m_0$ 为正态分布，相应的MFC方程就是：

$\{\begin{array}{l}-{\partial }_{t}u-\nu \Delta u+\frac{1}{2r{\left(1+m\right)}^{\beta }}{\left|Du\right|}^2-\frac{m\beta }{2{\left(1+m\right)}^{\beta +1}}{\left|Du\right|}^2=2\zeta m+\gamma \left(1-{\text{e}}^{-10{\left(x-0.25\right)}^2}\right)\hfill \\ {\partial }_{t}m-\nu \Delta m-\mathrm{div}\left(\frac{mDu}{{\left(1+m\right)}^{\beta }}\right)=0\hfill \\ u_T\left(x\right)=\left(-{\text{e}}^{-\omega *{\left(x-0.8\right)}^2}+1\right)\theta \hfill \\ m_0\left(x\right)=-{\text{e}}^{-10*{\left(x-0.2\right)}^2}\hfill \end{array}$ (19)

本例中我们对下面参数赋值 $\beta =0.5$ ， $r=1$ ， $\nu =0.05$ ， $\zeta =0.1$ ， $\gamma =1$ 和 $T=1$ ，由此给出对MFC的策略迭代算法(PI1)的结果。

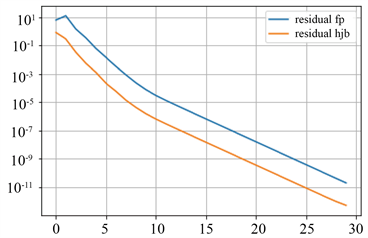
在图1中，通过绘制几个固定的n，我们分别展示了MFC数值模拟和MFG数值模拟的解密度分布随时间的演变。我们可以看到，解的密度分布都向同一个目标移动，而MFC方法更集中于目标附近。然而，由于拥堵成本和人群厌恶成本，两种方法都不能完全集中在目标上。在图2中，我们展示了与迭代次数为30的收敛结果：离散MFC和MFG系统的残差。这里我们使用了(PI1)算法获得的基准解。在这里我们观察到，通过我们的两种策略迭代方法得到的数值解是一致的，也侧面验证了之前的理论：除了前几次迭代和由于离散系统的近似精度限制而达到下限后以外，该收敛速度是线性的。

按照(18)计算本例中最优控制问题的社会总成本，即： $J_{mfc}$ 和 $J_{mfg}$ 。然后不管我们如何改变参数我们

得出 $\text{POA}=\frac{J_{mfc}}{J_{mfg}}$ 的值总是大于1。这也从数值解的角度验证了两类不同的社会总成本的优劣。

(a) (b)

Figure 1. Numerical solutions of Algorithm (PI1) of (19) at different times. (a) MFC; (b) MFG

图1. 算法(PI1)的(19)在不同时间下的数值解。(a) MFC；(b) MFG

(a) (b)

Figure 2. Convergence of Algorithm (PI1) of (19). (a) Residual of MFC; (b) Residual of MFG

图2. 算法(PI1)的(19)的收敛性。(a) MFC的残差；(b) MFG的残差

3.2. 计算POA

Carmona等 [11] 在对群体密度分布非局部依赖条件下，分析参数变化对POA的影响。而我们在对群体密度分布局部依赖条件下，使在时间T足够小时，我们通过有限差分法求出对应算法的数值解就可以计算相对准确的POA。在图3~9中，我们在不同参数设定下计算出不同的 $J_{mfc}$ 和 $J_{mfg}$ 。然后我们可以计算 $J_{mfg}$ 与 $J_{mfc}$ 的比率，它总是大于1。为了研究的严谨性，下面所有的例子都是基于一维实例(19)，除非另有说明，我们让参数保持在下面的默认值，对每类参数的影响都画出2组不同的POA图像。

$\begin{array}{llll}\beta =0.5,\hfill & \zeta =0.1,\hfill & \nu =0.08,\hfill & r=1,\hfill \\ \gamma =1,\hfill & T=1,\hfill & \omega =10,\hfill & \theta =1\hfill \end{array}$

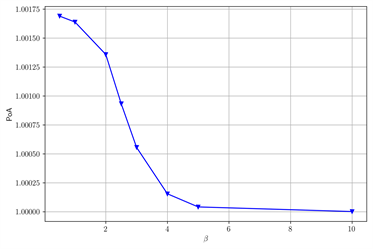
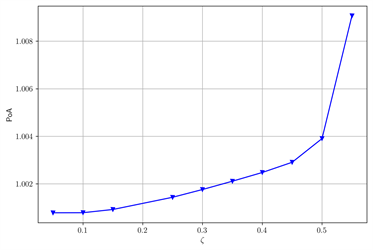
基于类似的不同参数情况下的对照实验，在图3中当β变大时，POA变小。在图4中当ζ变大时，POA变大。我们发现在图5中当r变大时，POA变小。

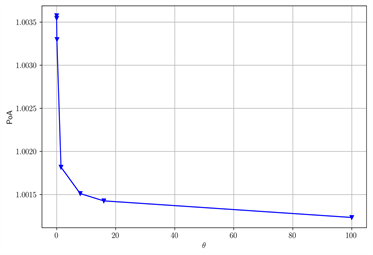
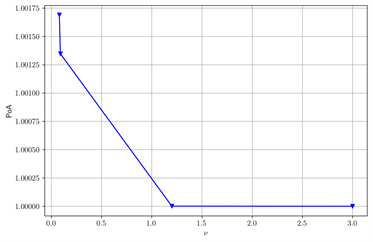
在图6中当γ变大时，POA变小。在图7中当T变大时，POA变大。在图8中当θ变大时，POA变小。在图9中当ν变大时，POA变小。我们重复不同数值下验证结果，得到类似的现象。这与Carmona 等 [11] 对POA影响的结果可以相互验证，我们在T足够小时，对局部依赖的条件，也分析了两类不同参数对POA的影响都是单调的但是方向不同。

(a) (b)

Figure 3. The change of POA with β after changing some parameters. (a) γ = 2.2; θ = 0.01; (b) ζ = 0.2

图3. 改变部分参数后，POA随β的变化。(a) γ = 2.2；θ = 0.01；(b) ζ = 0.2

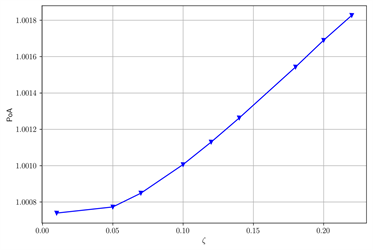(a) (b)

Figure 4. The change of POA with ζ after changing some parameters. (a) Default Parameters; (b) ν = 0.07, T = 0.3

图4. 改变部分参数后，POA随ζ的变化。(a) 默认参数；(b) ν = 0.07，T = 0.3

(a) (b)

Figure 5. The change of POA with r after changing some parameters. (a) ζ = 0.5, β = 2, γ = 1.8, T = 0.5, θ = 0.01; (b) ζ = 0.6, β = 1.8, γ = 1.8, T = 0.4, θ = 0.01

图5. 改变部分参数后，POA随r的变化。(a) ζ = 0.5，β = 2，γ = 1.8，T = 0.5，θ = 0.01；(b) ζ = 0.6，β = 1.8，γ = 1.8，T = 0.4，θ = 0.01

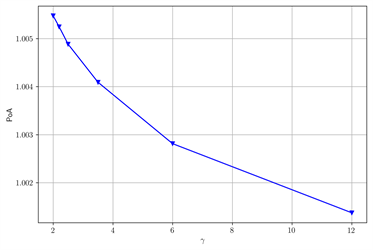(a) (b)

Figure 6. The change of POA with γ after changing some parameters. (a) ζ = 0.2, β = 0.8, ν = 0.06, T = 0.8, θ = 0.01; (b) ν = 0.07, ω = 100

图6. 改变部分参数后，POA随γ的变化。(a) ζ = 0.2，β = 0.8，ν = 0.06，T = 0.8，θ = 0.01；(b) ν = 0.07，ω = 100

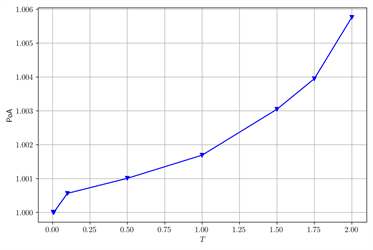(a) (b)

Figure 7. The change of POA with T after changing some parameters. (a) ζ = 0.2; (b) ν = 0.06

图7. 改变部分参数后，POA随T的变化。(a) ζ = 0.2；(b) ν = 0.06

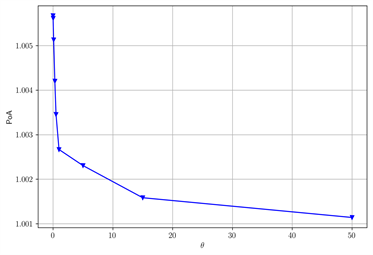(a) (b)

Figure 8. The change of POA with θ after changing some parameters. (a) β = 0.05, ν = 0.06, γ = 1.8; (b) β = 0.1, ν = 0.07, γ = 2.2

图8. 改变部分参数后，POA随θ的变化。(a) β = 0.05，ν = 0.06，γ = 1.8；(b) β = 0.1，ν = 0.07，γ = 2.2

(a) (b)

Figure 9. The change of POA with ν after changing some parameters. (a) β = 1, T = 0.5, γ = 5; (b) ζ = 0.2

图9. 改变部分参数后，POA随ν的变化。(a) β = 1，T = 0.5，γ = 5；(b) ζ = 0.2

4. 总结

本文研究的内容是一类来自于平均场控制问题的倒向–正向偏微分方程组有限差分数值计算方法，使用的算法基于最优控制问题中的策略迭代方法。其中，平均场偶合项是局部的，因此给解的正则性讨论和算法收敛性研究带来了新的困难。本文通过一些例子验证了算法的有效性。特别地，本文通过数值试验讨论了平均场博弈纳什均衡和平均场控制帕累托最优之间的总体效益比较。时间区域T较小的假设和相关的证明技巧导致本文提出的算法难以被从理论和实践上被用于更一般的情形，即使方程组可通过其他方法(Schauder不动点原理等)被证明解的存在性。同时，这种方法难以适用于方程组具有非唯一解的情况。这些问题有待进一步研究。