1. 引言
新型冠状病毒感染是一种由新型冠状病毒引起的急性传染性疾病,新冠病毒可在复制过程中不断适应宿主而产生突变。世界卫生组织(WHO)于2020年1月30日宣布将新型冠状病毒疫情列为“国际关注的突发公共卫生事件”,并且于2020年2月11日,WHO将由新型冠状病毒引发的疾病命名为2019冠状病毒病,英文名称为“Corona Virus Disease 19”(COVID-19) [1] 。同日,国际病毒命名委员会(ICTV)提议将新型冠状病毒命名为Severe Acute Respiratory Syndrome Coronavirus-2 (SARS-CoV-2) [2] 。截至 2023年3月29日,全球新型冠状病毒感染人数达761,402,282人,造成了61,887,000人的死亡 [3] 。
目前新型冠状病毒变异速度很快,以主要的流行毒株奥密克戎为例,其具有相当多的突变位点,其变异速度较快,且其下分支较多,导致其对疫苗的敏感性降低,接种疫苗人群仍旧有感染新型冠状病毒的风险 [4] [5] [6] ,随着时间推移,人体内的抗体含量持续下降,接种的疫苗在一定时间后会对人体的保护作用逐渐减弱,接种过疫苗的人体对新冠病毒的免疫能力也会下降 [7] ,因此我们考虑在接种疫苗的情况下对新型冠状病毒的影响。
近年来许多学者对新型冠状病毒的接种疫苗的分析从未停止,在 [8] 中Glenn Young等人建立了一个考虑接种的数学模型来分析新型冠状病毒的传播。研究表明由于新冠病毒疫苗接种率较低,在足够比例的人口接种疫苗之前,仍需实施非药物预防和其他控制措施来控制新型冠状病毒的传播。Cai等人 [9] 提出了具有年龄结构的新型冠状病毒随机动态模型,研究得出大多数新型冠状病毒死亡病例发生在未接种疫苗的人群中,尤其是老年群体中,得出提高老年人的接种率对减轻医疗负担有关键作用。Sun等人 [10] 考虑了医疗资源及接种疫苗等因素对新型冠状病毒的影响,建立了未接种人群与接种人群两群体分类讨论的动力学模型,分析了不同医疗资源及不同疫苗接种比例对上海新型冠状病毒的影响,得出了即使接种率达到100%,仍不能阻断新冠病毒传播的结论。Yang等人 [11] 提出了一个SVAIRS模型来分析新冠病毒是否可以通过单独接种疫苗完全消除,通过分析模型的基本再生数和平衡点的存在性,文章从理论上证明了仅仅依靠疫苗接种可能无法完全控制新型冠状病毒的传播。仍然有必要适当执行一些非药物干预措施。Tahir Khan等人 [12] 假设疫苗具有永久的免疫力,提出了SCAR数学模型,研究表明接种疫苗与新型冠状病毒的爆发有直接关系,快速的加大疫苗接种率,可以减少新型冠状病毒传播的持续时间。Mustafa等人 [13] 提出了SIRVI模型,模型中考虑接种疫苗后对于部分人群并不能提供完全有效的免疫力,导致这部分人依旧有感染新型冠状病毒的风险,通过分析表明通过疫苗接种可以有效控制新型冠状病毒的爆发。Julien Arino等人 [14] 提出了SLIARS动力学模型,进一步考虑了疫苗效能和疫苗免疫的减弱对新型冠状病毒的影响,通过动力学分析得出系统存在后向分支,并且对该模型的连续时间马尔可夫链(CTMC)进行了数值模拟,检测出后向分岔的存在性。上述学者都考虑了接种疫苗对新冠病毒传播的影响,对具有接种疫苗的传染病建模有较完善的理论研究,但是随着时间的推移,人体内中和抗体水平下降,疫苗的保护作用减弱,同时由于新型冠状病毒变异速度较快,具有较强的免疫逃逸能力,对于疫苗失效的情况的研究有所欠缺。
本文以上海新型冠状病毒的传播为例,将接种人群单独考虑为一个仓室建立了数学模型,研究了其内在机理。本文的研究结构如下:在第2节中给出了具有接种的新型冠状病毒模型及其参数的描述,第3节利用定性理论证明了正平衡点的存在性、全局稳定性。第4节运用MCMC法进行参数估计,然后根据得出的参数对上海2022年2月26~2022年5月31日的数据进行拟合,文中我们根据上海当时采取的政策将分为三个阶段处理,计算出了三个阶段的基本再生数,并且对基本再生数进行敏感性分析,然后分析不同的每日接种率和初始接种率对上海新型冠状病毒传播的影响。最后在第5节中讨论主要的结果。
2. 模型的建立
在这一部分中,我们构建
模型来分析接种疫苗对新型冠状病毒的影响,把总人口分为八个仓室:未接种疫苗的易感者
.接种疫苗的易感者
、暴露者
、有症状染病者
、无症状染病者
、确诊病例
、恢复者
,以及因确诊新型冠状病毒而死亡者
,且有
,由于死亡仓室不影响模型的动力学分析,所以将死亡的确诊病例可以单独表示为
,对模型作如下假设:模型中采用双线性发生率;不考虑人口迁移对新型冠状病毒的影响,且新生儿不能接种疫苗;考虑到新型冠状病毒的传播方式有易感个体可以通过接触无症状和有症状的染病者而感染。可以得到流程图见图1:

Figure 1. The flow chart of novel coronavirus propagation with vaccination
图1. 具有接种的新型冠状病毒传播流程图
根据上述流程图,可以得到如下常微分方程组:
(1)
记为系统(1),其中系统(1)中的参数及其所代表的意义如下(表1):

Table 1. Description of parameters in system (1)
表1. 系统(1)中参数的描述
3. 动力学行为
系统(1)总存在一个无病平衡点
且系统(1)的可行域是正不变集
,其中
。
3.1. 基本再生数
根据文章 [15] [16] 基本再生数以及下一代矩阵的定义,定义一组向量
,仅包含系统(1)的致病项,由文章 [15] 的方法可得:
其中
是非负矩阵,
是非奇异矩阵
基本再生数
,
是矩阵的谱半径
计算可得基本再生数为:
其中:
3.2. 稳定性分析
令系统(1)的右端为0,可以求得正平衡点
其中
(2)
显然可知
,现在证明
,令
,对
求导得:
即
是关于
的单调递增函数,当
等于0时
最小,计算得
,故证得
。
接着我们将(2)代入系统 ,可得关于
的表达式为
;且有
(3)
其中:
当
时,有
,此时
只有唯一一个正根,即系统(1)只有唯一一个正平衡点。
当
时,
,根据
将其代入b得
此时
,
没有正根,即系统(1)只存在一个无病平衡点。
当
时,
,根据
将其代入b得
此时由
得,
没有正根,即系统(1)只存在一个无病平衡点。
综上所述,只有当
时,系统(1)存在唯一一个正平衡点。
定理1:当
时,系统(1)的无病平衡点在正不变集
内是局部渐进稳定的。
证明:
令
,由参考文献的 [15] 定理2可得
在无病平衡点处得雅可比矩阵为
,其中
,
计算
的特征值可得:
,即
,有
且
,可知系统(1)的无病平衡点在
是局部渐进稳定的。
定理2:当
时,系统(1)的无病平衡点在正不变集
内是全局渐进稳定的。
证明:对于无病平衡点
,模型可以重新写作如下形式,记为系统(4)
(4)
假设
为系统(4)的任意正解,构造一个Lyapunov函数
V沿系统(4)的全导数为
令
(5)
得出
(6)
代入其中得
由上述可知当
时,
当且仅当
,时
,即
是系统(1)的最大不变集,由LaSalle不变集原理 [17] 可以得出无病平衡点
是全局渐进稳定的。
定理3:当
时,系统(1)的正平衡点
在正不变集
内是全局渐进稳定的。
证明:
令
模型可以重新写作如下形式:记为系统(7)
(7)
可以看出系统(7)有唯一一个正平衡点
,现证明
的全局稳定性。
构造一个Lyapunov函数:
V沿系统(7)的全导数为
令模型(1)等于0且代入
得
(8)
代入得:
由上述可知
当且仅当即
时
,由LaSalle不
变集原理 [17] 可以得出唯一的正平衡点 是全局渐进稳定的。
4. 数值模拟和敏感性分析
4.1. 参数估计
因为上海在2月底开始爆发新型冠状病毒感染,于6月1日开始解封,故此处用上海2022年2月26日至2022年5月31日的报导的病例数据 [18] 来验证模型的精确性,模拟在此期间的累计确诊病例,用
代表累计确诊病例,所以有
此段时间内上海报告了60多万例当地的新型冠状病毒病例,根据上海政府在此期间采取的防控措施的变化,我们将此地新冠病毒的传播分为三个阶段,第一阶段是2022年2月26日至3月28日的阶段,假设它是没有任何干预的自由传播阶段。此时病例数目较少,也没有死亡病例出现,此时p = 0.04,d = 0 [18] ,随着新冠病毒的爆发,上海政府从2022年3月28日开始采取封控措施,在此期间上海基本属于封锁阶段,除了医务工作人员外,其他人几乎都待在家里,在2022年3月28日至4月16日,此时属于刚采取封控的前半个月,由于封控较晚,已经造成了社会性的传播,由于新型冠状病毒的潜伏期短,无症状染病者占绝大多数,所以即使在封控期间,会出现大量的染病者,政府在此期间采取了频繁的大规模核酸检测,导致聚集现象较多发生,因此在人群中有大量潜伏者以及无症状的感染者,易感者会与做核酸的染病者接触导致被感染,因在此期间,核酸检测频率增多,易感者被感染的机会增多,所以传染率比第一阶段增大,随着染病者的增多,医疗资源相对紧张,导致有一部人染病者不能及时被确诊。此时
比第一阶段小,p = 0.064303379,d = 0 [18] ,第三阶段是2022年4月16日至5月31日,经过半个月的封控,每日报告的染病人数开始下降,绝大多数染病者都是在封控区被查出来,易感者与染病者接触的机会减少,以及核酸检测也有序排队,聚集现象较少发生,虽然每日报告的染病人数开始下降,但总体染病人数一直增加,所以假设染病者的确诊率还是下降的,此时p = 0.12680221,d = 0.02642364 [18] 。所以我们将分三个阶段来进行数值模拟,首先给出已知的参数,根据参考文献 [10] ,奥密克戎的平均潜伏期为1.52天,根据新型冠状病毒流行数据知,无症状人群相对有症状人群的传染性η = 0.75 [10] [19] ;由于新型冠状病毒可能逃避疫苗的免疫,中和抗体导致现有疫苗对抗奥秘克戎的有效性降低,假设θ = 0.8;假设接种疫苗的平均有效期为1年,x = 0.0028,同时考虑到疫情爆发期间,接种人数较少,所以假设持续接种率为v = 0.001,由 [20] 知,2022年上海出生人数为Λ = 288,自然死亡率为
,根据 [10] 假设无症状染病者的平均染病时间
,确诊病例的平均染病时间
,上海的总人口为24871100,新型冠状病毒的平均疫苗接种率为72.6% [21] 。将初始值设置为
;其中
我们用最小二乘法进行拟合,对于未知的参数
,文中我们使用马尔可夫链蒙特卡洛法(MCMC) [21] 来进行估计。估计结果见表2,最后我们利用估计所得的参数计算三个阶段的基本再生数见表3。
4.2. 拟合结果
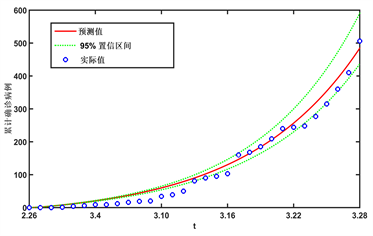
图2显示了上海2022.2.26~2022.5.31期间估计的累计确诊病例和实际确诊病例,并给出了模拟结果的95%置信区间。

Table 2. Parameter estimation with the method of MCMC (95% confidence interval)
表2. 使用MCMC方法进行参数估计(95%置信区间)

Table 3. Estimation of the value Rv in different stages (95% confidence interval)
表3. 不同阶段Rv的估计值(95%置信区间)
 (a)
(a) 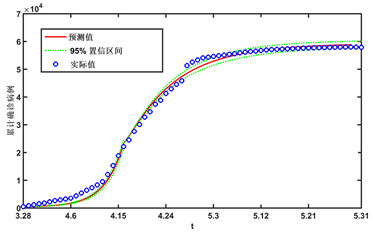 (b)
(b)
Figure 2. (a) Fitting results of cases in Shanghai from 2022.2.26 to 2022.3.28; (b) Fitting results of cases in Shanghai from 2022.3.28 to 2022.5.31
图2. (a) 2022.2.26~2022.3.28上海累计确诊病例的拟合结果;(b) 2022.3.28~2022.5.31上海累计确诊病例的拟合结果
4.3. 敏感性分析
基本再生数
是预测疾病是否会发生的阈值指数,因此确定模型(1)中对
有重大影响的控制参数至关重要,以便进行相应的控制措施来消除疾病。表4给出基本再生数
对每一个参数l的归一化敏感
性指数
[22] 。
根据表4可以看出
与
呈正相关,即
随着这些参数的增加而增加,意味着新型冠状病毒的流行更严重,而
与
呈负相关。意味着增大这些参数可以减小基本再生数,从而控制新型冠状病毒的流行。因此可得结论:阻断传播、提高易感人群的接种率、提高疫苗的有效性、以及提高确诊率是控制新冠病毒的有效措施。为了更好的分析接种疫苗对新型冠状病毒传播的影响,我们考虑第一阶段,即在自由传播状态下参数对
的影响。首先考虑单个参数对
的影响,先考虑对
影响较大的
和
见图3、从图3(a)、图3(b)可以看出如果
,意味着新冠病毒将消失,从敏感性指数可知v和x对
影响较小,从图3(c)、图3(d)可以看出即使每日接种率为100%,疫苗有效率为100%,
仍大于1,意味着新冠病毒并不会消失。即仅靠接种疫苗并不能完全阻断新型冠状病毒的传播,应该采取其他措施来控制疾病。接下来看图4所示的两个参数对
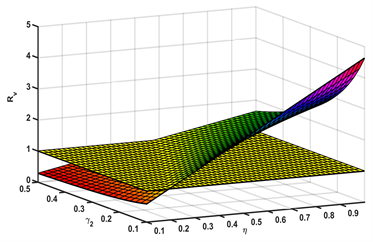
的综合影响,从图4(a)中可以看到,在
和
的联合作用下,
可以迅速减小。从图4(b)中还可以看到
和
的阈值,以保持
。
 (a)
(a) 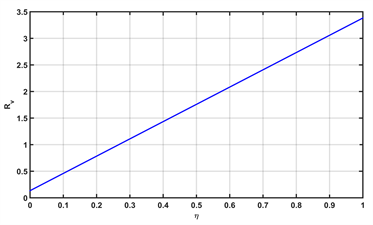 (b)
(b)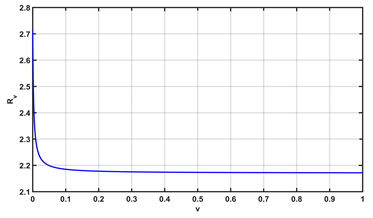 (c)
(c) (d)
(d)
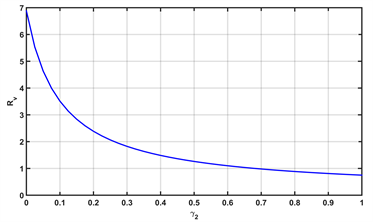
Figure 3. The influence of parameters
,
, v and x on the basic reproduction number Rv: (a) Rv in terms of different
; (b) Rv in terms of different
; (c) Rv in terms of different v; (d) Rv in terms of different x
图3. 参数
对基本再生数Rv的影响:(a)
对Rv的影响;(b)
对Rv的影响;(c) v对Rv的影响;(d) x对Rv的影响
 (a)
(a) 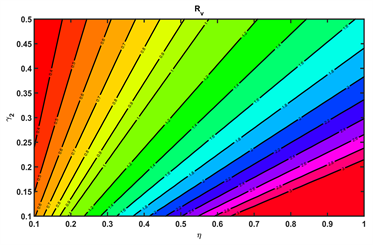 (b)
(b)
Figure 4. Rv in terms of parameters
and
.
图4.
和
对
的影响
4.4. 接种率对新型冠状病毒确诊病例数的影响
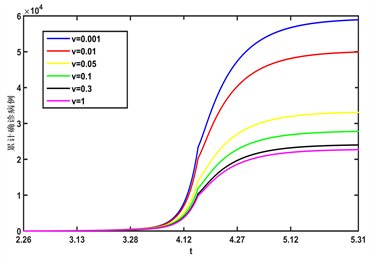
为研究每日不同疫苗接种率、以及初始接种率对上海新型冠状病毒确诊病例的影响,下面给出通过变化v以及初始接种率后,所得到的相应的确诊病例数见图5,分别选取v = 0.001,v = 0.01,v = 0.05,v = 0.1,v = 0.3,v = 1,图5(a)显示随着v的增大,累计确诊病例数将减少,所以提高每日的接种率对新型冠状病毒的传播有抑制作用,但即使v = 1,上海新型冠状病毒累计确诊病例数仍有22,600。根据参考文献 [9] ,上海居民的新型冠状病毒初始接种率为72.6%,分别选取初始接种率为80%,85%,90%,95%,100%,图5(b)显示随着初始疫苗接种覆盖率的增加,上海累计确诊病例数将减少,因此我们应该尽可能扩大新型冠状病毒疫苗的推广范围以达到最大值,然而当疫苗的初始覆盖率达到100%,我们可以观察到上海累计确诊病例数将减少到27490,这表明疫苗接种可以适度缓解新型冠状病毒的传播,但是不是一项完整的控制措施,因此我们需要寻求其他策略来阻止新型冠状病毒在上海的传播,例如广泛的抗病毒药物等。
 (a)
(a) 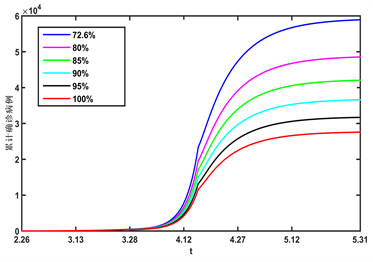 (b)
(b)
Figure 5. (a) With different v values, the cumulative confirmed cases’ trajectory over time; (b) With different initial vaccination rate, the cumulative confirmed cases’ over time
图5. (a) 取不同的每日接种率v,累计确诊病例随时间变化的轨迹;(b) 取不同的初始接种率,累计确诊病例随时间变化的轨迹
5. 结论
基于2022年2月至5月上海新冠病毒传播的具体特点,我们建立了一个数学模型,模型中我们考虑具有持续的疫苗接种以及疫苗具有有效期,同时考虑疫苗并不能对人体起到100%的保护作用,即接种疫苗的人群仍有被感染新冠病毒的可能,我们建立此模型以研究接种疫苗对于上海此次新冠病毒传播的影响。首先我们根据下一代矩阵方法计算了模型的基本再生数,证明了平衡点的存在个数及其条件,通过构造Lyapunov函数证明了无病平衡点以及
时唯一的正平衡点的稳定性。然后我们收集了上海卫生健康委员会于2022年2月26日至5月31日报告的确诊病例数据,并根据政府采取的一系列控制干预措施,将整个传播过程分为三个阶段。我们马尔可夫链蒙特卡洛法(MCMC)来估计模型的参数,并使用累积确诊病例数来验证模型的准确性,数值模拟结果如图2所示。且通过计算可得上海三个阶段的基本再生数分别为2.5709、5.1583、0.2982,意味着新型冠状病毒在上海最终会消失。根据求得的参数,对
进行敏感性分析,并在图3中和图4我们分别画出了单个参数
对
的影响以及两个参数
对
的影响。其次我们考虑了在不同的控制措施下对上海新冠病毒传播的最终规模的影响。根据图5我们可以得到提高每日的接种比例以及初始接种比例,能够有效降低确病例,从而降低疾病的传染规模。并且随着接种比例的增大,确诊人数减少,但是即使初始接种人数为100%,或者每日接种比例为100%,并不能完全阻断传染病的传播。所以我们应该采取其他方法来控制新型冠状病毒的传播,例如广泛的抗病毒药物等。然而本文也存在许多限制。首先我们认为所有人的传染率都是一样的。然而研究表明不同年龄结构对感染风险的影响异质性是不同的,这些留给我们在未来的工作中学习。
NOTES
*通讯作者。