数形结合法在《概率论与数理统计》教学中的应用

The Application of Method of Combination of Figure and Chart in the Teaching of Probability Theory and Mathematical Statistics

摘要: 在《概率论与数理统计》课程的教学中，二维连续型随机变量的相关知识的教学是一个重要的内容，而其中边际密度以及两个随机变量和的密度函数的求解问题是重点和难点问题，本文利用数形结合的思想，用一幅坐标图轻松的解决了这个问题。结果表明数形结合法是一个有效的解决此类问题的方法。

Abstract: In the teaching of probability theory and mathematical statistics, the teaching of relevant knowledge of two-dimensional continuous random variables is an important content, in which, the solution of marginal density and the density function of the sum of two random variables is a key and difficult problem. In this paper, the combination of figure and chart which only use a pair of co-ordinates is proposed to solve this problem. The results show that the combination of figure and chart is an effective method to solve such problems.

1. 引言

《概率论与数理统计》是我国各大高校中理、工、管理类等各专业的最重要的数学基础课之一，学好这门课程可以为学生的后续学习和研究工作打下良好的基础。但是，本门课程也是大学生普遍反应比较难学的一门课程，有些学生虽然理解了一些基本概念并记住了相应的公式，但是在具体求解题目时，由于不注重解题方法而得到错误的答案。而二维连续型随机变量的边际密度以及两个随机变量和的密度函数的求解问题，是一类典型的易错问题，也是《概率论与数理统计》教学中的一个难点问题 [1] ，主要体现在积分限和所求函数的非零区间的确定上。

数形结合法 [2] - [7] 是数学教学中的一种重要思想方法。该方法将数学问题和图形有效结合，将抽象的难以理解的问题图形化、直观化，使所求解问题简单形象易懂，从而可以使学生直观地解决数学问题，更好的理解其中的数学思想和方法。因此，将数形结合的思想和方法应用于数学教学中，可以使学生更好的学，使老师更容易的教。本文通过几个具体的例子，运用数形结合的方法求解边际密度以及随机变量和的密度的求解问题。事实上，作者在《概率论与数理统计》课堂教学中多次使用该方法，而广大学生能很快掌握此方法解决此类问题，作者认为此方法值得推广。

2. 用数形结合法求解二维连续型随机变量的边际密度函数的问题

二维连续型随机变量的边际密度问题的一般提法为：设二维连续型随机变量(X, Y)的联合密度函数为f(x, y)，求(X, Y)的边际密度函数f_X(x)和f_Y(y)。此问题可以用如下两个公式求解

$f_X\left(x\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,y\right)\text{d}y}$ ， $f_Y\left(y\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,y\right)\text{d}x}$

这个问题的公式比较简单，但是在具体题目中，由于联合密度函数f(x, y)一般只在某个区域上非零(记此非零区域为D)，所以求得的两个边际密度函数f_X(x)和f_Y(y)一般是分段函数。此时，分段函数的非零区间以及对应的积分的上限和下限比较难确定，这也是学生在学习中容易出错的地方。利用数形结合法可以很容易的解决这个难点问题。下面我们结合几个例子说明如何用数形结合法求解此类问题。

例1. 设二维连续型随机变量(X, Y)的联合密度函数为

$f\left(x,y\right)=\{\begin{array}{cc}1,& 0\le x\le 1,0<y<2x\\ 0,& 其它\end{array}$

求随机变量X和Y的边际密度函数f_X(x)和f_Y(y)。

分析：此问题是比较典型的边际密度问题的题型。由于在联合密度函数f(x, y)中，明确告知了x和y的范围，一般来说，同学们在求解X的边际密度时不容易出错，即可以直接得出f_X(x)的非零区间为0 £ x

< 1，此时关于y的积分 ${\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,y\right)\text{d}y}$ 对应的积分上限和下限也分别是0和2x，即有 ${\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,y\right)\text{d}y}={\displaystyle \underset{0}{\overset{2x}{\int }}f\left(x,y\right)\text{d}y}$ 。但当求解Y的边际密度函数f_Y(y)时，同学们常常会犯错误，将f_Y(y)的非零区间直接写为0 £ y < 2x，而关于x的积分 ${\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,y\right)\text{d}y}$ 的积分上限和下限直接写为0和1，即 ${\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,y\right)\text{d}y}={\displaystyle \underset{0}{\overset{1}{\int }}f\left(x,y\right)\text{d}y}$ 。错误的主要原因可以归结为对函数的概念和积分的应用的错误理解上。由于

联合密度函数函数f(x, y)完全已知，所以f_Y(y)一定是一个确定的函数，因此在其非零区间的取值范围中，不应该含有另一个自变量x；而当正确给出非零区间的范围后，关于x的积分限是由f(x, y)的非零区域给定的，此时应该和y有关系，故不应该是0和1的积分上限和下限.实际上，两个边际密度函数非零区间以及对应的积分的上限和下限都是由联合密度函数f(x, y)的非零区域确定的。利用数形结合法可以将此问题简单化、直观化。

解：先求X的边际密度函数，由公式可得

$f_X\left(x\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,y\right)\text{d}y}$

为了求此积分，绘制关于f(x, y)的如下图形。如图1所示。

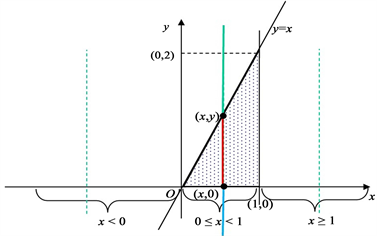
Figure 1. Graph used to calculate f_X(x)

图1. 求f_X(x)所用图形

图中的三角形区域就是f(x, y)的非零区域。从图中可以看出，整个x轴被分成三段，x < 0，0 £ x £ 1和x > 1。且当x < 0或者x > 1时，对于任意固定的x的值，f(x, y) = 0。当0 £ x £ 1时，对任意固定的x，f(x, y)关于自变量y为一个分段函数，

$f\left(x,y\right)=\{\begin{array}{cc}0,& y<0\\ 1,& 0<y<2x\\ 0,& y\ge 2x\end{array}$

因此有：当x < 0或者x > 1时

$f_X\left(x\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,y\right)\text{d}y}={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}0\text{d}y}=0$

当0 £ x £ 1时

$f_X\left(x\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,y\right)\text{d}y}={\displaystyle \underset{-\infty }{\overset{0}{\int }}0\text{d}y}+{\displaystyle \underset{0}{\overset{2x}{\int }}1\text{d}y}+{\displaystyle \underset{2x}{\overset{+\infty }{\int }}0\text{d}y}={\displaystyle \underset{0}{\overset{2x}{\int }}1\text{d}y}=2x$

所以，X的边际密度函数为

$f_X\left(x\right)=\{\begin{array}{cc}2x,& 0\le x\le 1\\ 0,& 其它\end{array}$

下面用数形结合法求Y的边际密度函数。绘制如图2所示的图形。

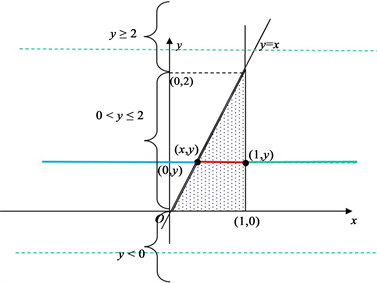
Figure 2. Graph used to calculate f_Y(y)

图2. 求f_Y(y)所用图形

从图中可以看出，整个y轴被分成三段，y < 0，0 £ y £ 2和y > 2。且当y < 0或者y > 2时，对于任意固定的y的值，f(x, y) = 0。当0 £ y £ 2时，对任意固定的y，f(x, y)关于自变量x为一个分段函数，

$f\left(x,y\right)=\{\begin{array}{cc}0,& x<y\\ 1,& y<x<1\\ 0,& x\ge 1\end{array}$

因此，当y < 0或者y > 2时，

$f_Y\left(y\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,y\right)\text{d}y}={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}0\text{d}x}=0$

当0 £ y £ 2时，

$f_Y\left(y\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,y\right)\text{d}y}={\displaystyle \underset{-\infty }{\overset{y}{\int }}0\text{d}x}+{\displaystyle \underset{y}{\overset{1}{\int }}1\text{d}x}+{\displaystyle \underset{1}{\overset{+\infty }{\int }}0\text{d}x}={\displaystyle \underset{y}{\overset{1}{\int }}1\text{d}x}=1-y$

所以，Y的边际密度函数为

$f_Y\left(y\right)=\{\begin{array}{cc}1-y,& 0\le y\le 2\\ 0,& 其它\end{array}$

总结以上解题过程，为了得到两个边际密度函数的非零区间和积分的上、下限，只需要将f(x, y)的非零区域表示为两种不同的形式即可。由图1可以看出，可以将三角形的非零区域表示为 $D=\left\{0\le x\le \text{1},0<y<x\right\}$ ，而0 £ x £ 1对应f_X(x)的非零区间，0 < y < x对应积分的上下限。由图2可得，三角形非零区域表示为 $D=\left\{0\le y\le 2,y<x<1\right\}$ ，而0 £ y £ 2对应f_Y(y)的非零区间，y < x < 1对应积分的上下限。

通过例1，我们看到，利用数形结合法，可以将复杂的积分问题，运用绘制坐标图的方法轻松而快速的找到解决方案。下面再看一个更复杂的例题。

例2. 设二维连续型随机变量(X, Y)的联合密度函数为

$f\left(x,y\right)=\{\begin{array}{cc}\frac{x}{2},& \left|y\right|<x<2-\left|y\right|\\ 0,& 其他\end{array}$

求随机变量X和Y的边际密度函数为f_X(x)和f_Y(y)。

分析：此问题中没有明确的告诉大家自变量x和y的边界值，使得问题的求解更加复杂。下面我们利用数形结合法解决此问题。

解：将联合密函数f(x, y)的非零区域表示在图3的坐标系中。

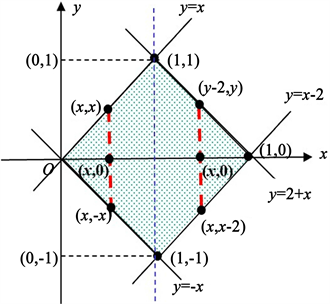
Figure 3. Graph used for finding f_X(x)

图3. 求f_X(x)所用图形

由图3知，f(x, y)的非零区域可以表示为

$\{\begin{array}{c}0<x<1\\ -x<y<x\end{array}+\{\begin{array}{c}1\le x<2\\ x-2<y<2-x\end{array}$

所以X的边际密度函数为

$f_X\left(x\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,y\right)\text{d}y}=\{\begin{array}{cc}{\displaystyle \underset{-x}{\overset{x}{\int }}\frac{x}{2}\text{d}y},& 0<x<1\\ {\displaystyle \underset{x-2}{\overset{2-x}{\int }}\frac{x}{2}\text{d}y},& 1\le x<2\\ 0,& 其它\end{array}=\{\begin{array}{cc}{x}^2,& 0<x<1\\ 2x-x^2,& 1\le x<2\\ 0,& 其它\end{array}$

同样的方法，可以将联合密函数f(x, y)的非零区域表示在图4的坐标系中。

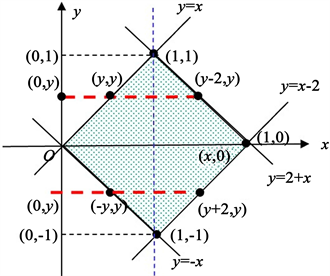
Figure 4. Graph used to calculate f_Y(y)

图4. 求f_Y(y)所用图形

由图4知，f(x, y)的非零区域可以表示为

$\{\begin{array}{c}-1<y<0\\ -y<x<y+2\end{array}+\{\begin{array}{c}0\le y<1\\ y<x<2-y\end{array}$

所以Y的边际密度函数为

$f_Y\left(y\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,y\right)\text{d}y}=\{\begin{array}{cc}{\displaystyle \underset{-y}{\overset{y+2}{\int }}\frac{x}{2}\text{d}x},& -1<y<0\\ {\displaystyle \underset{y}{\overset{2-y}{\int }}\frac{x}{2}\text{d}x},& 0\le y<1\\ 0,& 其它\end{array}=\{\begin{array}{cc}1+y,& -1<y<0\\ 1-y,& 0\le y<1\\ 0,& 其它\end{array}$

由以上2个例题可以看出，利用数形结合法可以直观、快速的确定边际密度中的函数的非零区间和积分限。

3. 用数形结合法求解二维连续型随机变量和的密度函数的问题

在二维连续型随机变量的教学中，随机变量和的分布的求解问题是重要的问题之一，也是学生比较容易出错的一个知识点 [1] 。此问题的一般提法是： 设二维连续型随机变量(X, Y)的联合密度函数为f(x, y)，求Z = X + Y的密度函数f_Z(z)。此问题可以用如下两个公式进行求解，

$f_Z\left(z\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,z-x\right)\text{d}x}$ ， $f_Z\left(z\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(z-y,y\right)\text{d}y}$

和的密度函数的求解的难点也是容易出错的地方也是f_Z(z)的非零区间以及对应的积分限的确定。通过下面的例题，我们可以看到这个问题可以轻松的被解决。

例3. 设二维连续型随机变量(X, Y)的联合密度函数为

$f\left(x,y\right)=\{\begin{array}{cc}1,& 0\le x\le 1,0<y<2x\\ 0,& 其它\end{array}$

求Z = X + Y的密度函数f_Z(z)。

解：利用公式 $f_Z\left(z\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,z-x\right)\text{d}x}$ 求解此问题。

其中 $f\left(x,z-x\right)=\{\begin{array}{cc}1,& 0\le x\le 1,x<z<3x\\ 0,& 其它\end{array}$

将此函数的非零区域表示在图5的坐标系中。

Figure 5. Graph used for finding fZ (z)

图5. 求f_Z(z)所用图形

由图5知，f(x, z-x)的非零区域可以表示为

$\{\begin{array}{c}0\le z\le 1\\ z/3<x<z\end{array}+\{\begin{array}{c}1<z\le 3\\ z/3<x<1\end{array}$

所以Z的密度函数为

$f_Z\left(z\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f\left(x,z-x\right)\text{d}x}=\{\begin{array}{cc}{\displaystyle \underset{z/3}{\overset{z}{\int }}1\text{d}x},& 0\le z\le 1\\ {\displaystyle \underset{z/3}{\overset{1}{\int }}1\text{d}x},& 1<z\le 3\\ 0,& 其他\end{array}=\{\begin{array}{cc}\frac{2z}{3},& 0\le z\le 1\\ 1-\frac{z}{3},& 1<z\le 3\\ 0,& 其他\end{array}$

4. 总结

从以上三个例题中可以看出，在《概率论与数理统计》的教学中，利用数形结合的思想可以将教学中的难点问题、复杂问题图形化、简单化、直观化，从而可以使同学们更加轻松的掌握解决这类问题的方法，有效提高学生的学习效率，提升教学效果。