R-UHPC梁抗剪承载力有限元分析

Finite Element Analysis of Shear Capacity of R-UHPC Beam

摘要: 为研究配筋超高性能混凝土(R-UHPC)梁的抗剪性能，结合6根不同钢纤维掺量和配箍率的R-UHPC梁受剪破坏试验，通过有限元参数分析，验证了极限荷载、纵筋应变、箍筋应变、开裂情况，得出剪跨比为1.2~2.8范围的R-UHPC梁抗剪承载力及变化规律。

Abstract: In order to study the shear behavior of R-UHPC beams with reinforcements, combined with shear failure tests of 6 R-UHPC beams with different steel fiber content and reinforcement ratio, the ultimate load, longitudinal bar strain, stirrup strain and cracking were verified by finite element parameter analysis, and the shear bearing capacity and variation rule of R-UHPC beams with shear span ratio of 1.2~2.8 were obtained.

1. 引言

超高性能混凝土(Ultra-High Performance Concrete, UHPC)有着高强度、高韧性、徐变小和耐久性好等特点，广泛地被应用于桥梁、建筑、水利和海洋等领域 [1] 。UHPC梁的受剪破坏现象复杂，是当前结构工程的研究热点。

为探究UHPC梁的剪切破坏机理，国内外学者进行了一系列试验研究。Pourbaba [2] 等对19根UHPC梁、19根普通混凝土梁进行了受剪性能试验，结果表明，UHPC梁的平均抗剪能力是普通混凝土梁的3.5倍，挠度是普通混凝土梁的2.5倍；剪跨比的增加会降低梁的受剪承载力和刚度，提高梁的变形能力 [3] [4] [5] [6] ；梁兴文 [7] 等对7根UHPC梁进行了受剪性能试验，研究了剪跨比、纵筋配筋率、配箍率和钢纤维体积掺量对抗剪承载力的影响，结果表明，UHPC梁中纵筋销栓作用对抗剪承载力的贡献较大，在抗剪分析中应考虑；Voo [8] 等对8根UHPC梁进行了受剪性能试验，结果表明，在混凝土基体中使用钢纤维会增加梁体开裂后的韧性，在大裂缝开口时保持较高的抗拉强度，有必要进一步建立考虑钢纤维影响的UHPC梁抗剪承载力设计理论模型。

为此，本文结合试验和有限元参数分析，验证了极限荷载、纵筋应变、箍筋应变、开裂情况，得出剪跨比为1.2~2.8范围的R-UHPC梁抗剪承载力及变化规律。

2. 试验概况

为研究UHPC梁受剪力学性能，进行了4根无腹筋和2根有腹筋的矩形UHPC梁的抗剪试验。试验梁梁长1200 mm，计算跨度1000 mm。为提高梁的抗弯承载力，确保试验梁为受剪破坏，在试验梁底部配置足够的纵向受力钢筋。试验参数主要有UHPC的钢纤维掺量、箍筋配箍率和混凝土抗压强度。以1%钢纤维掺量的R-UHPC梁S1为基础，分别变化钢纤维体积掺量0.5%、1.5%和2%，相应的梁为试验梁S2、S3和S4；变化箍筋配箍率的是试验梁S5、S6，加上S1，成为配箍率变化的一组。梁截面尺寸与配筋如图1。

(a) L1~L4 (b) L5、L6

Figure 1. Section size and reinforcement of UHPC test beam (cm)

图1. UHPC试验梁截面尺寸及配筋图(cm)

试验梁梁长1200 mm，计算跨度1000 mm，配筋均使用HRB400钢筋，各参数见表1。表中， ${\rho }_f$ 表示钢纤维体积掺量， ${\rho }_{sv}$ 为箍筋配筋率，λ为剪跨比。极限荷载为千斤顶所施加的力F，抗剪荷载 $V=F/2$ 。

Table 1. Parameters of UHPC test beam

表1. UHPC试验梁参数表

UHPC材料性能见表2，f_cu对UHPC为立方体抗压强度，f_w为UHPC的抗折强度；f_t为直拉试验测得的直拉强度；E_c为UHPC的抗压弹性模量。

Table 2. Material performance test results

表2. 材料性能试验结果

试验梁两端简支，通过2000 kN电液伺服压力机进行单点加载，在试验过程中，记录试验梁混凝土与钢筋应变、梁的挠度等，试验梁加载装置如图2所示。

Figure 2. Layout of beam loading device and measuring points (mm)

图2. 梁加载装置及测点布置图(mm)

3. 有限元

3.1. 有限元建模

为更好地在ANSYS中找到适合R-UHPC梁的建模方式，本文进行了一系列精细化仿真分析，混凝土使用高阶实体单元SOLID186，搭配MWC和HSD模型定义本构关系模拟UHPC的受拉和受压行为；钢筋使用REINF264单元模拟，本构关系采用双线性等向强化模型BISO，使用双直线定义材料的应力–应变关系；加载位置的垫块与混凝土实体之间应设置为摩擦接触；将混凝土实体的网格尺寸控制在保护层厚度的1~2倍，同时应保证REINF加强筋单元的体积比不宜过小；使用位移加载和位移收敛准则，提升计算的收敛性，更易获得混凝土梁的极限荷载和下降段。为得到结构的极限承载力，加载值在预估的极限承载能力上进行适当放大，初始子步定为100，最小子步为100，最大子步为1000，将默认为25的迭代次数增大到200，有限元模型如图3。

Figure 3. Finite element model

图3. 有限元模型图

3.2. 模型验证

(一) 极限荷载

对6根试验梁进行模拟，将极限荷载试验值与有限元计算结果的剪力值比较，汇总于表3，根据比较结果比值的平均值为1.01，标准差为0.01，相关性系数为0.99。

Table 3. Comparison of ultimate load test values and finite element calculation results

表3. 极限荷载试验值与有限元计算结果比较

(二) 纵筋应变

以试验梁S1为代表，对比纵筋的荷载–应变曲线绘于图4。图中可见，S1实测的荷载–应变曲线与有限元模拟结果基本吻合，在荷载达到300 kN之后，相同荷载下有限元计算的纵筋应变要比实测值略微偏小，这是由于有限元模型采用对称建模的方式，梁体左右破坏情况相同，属于更为理想的破坏状态。

Figure 4. Comparison of load-strain curves of longitudinal reinforcement S1

图4. S1纵筋荷载–应变曲线比较

(三) 箍筋应变

箍筋的荷载–应变对比情况以试验梁S5为例，将有限元计算值与S5实测值绘于图5。图中可见，计算值与试验值吻合良好，且有限元计算值可以在梁达到极限荷载后获得更长的应变数据，这是因为在计算梁在达到极限荷载之后，相较试验可以继续加载得到更长的荷载下降段。

Figure 5. Load-strain curve comparison of S5 stirrups

图5. S5箍筋荷载–应变曲线对比

(四) 开裂情况

以有腹筋梁S5为例，将有限元模拟的等效塑性应变云图与试验实测的裂缝分布分别绘于图6。等效塑性应变云图中除去深蓝色的剩余区域为有限元分析的裂缝分布范围，红、黄色位置为塑性应变最大的区域。图6(b)可见，在达到极限荷载819 kN时，试验梁在剪跨区出现了1.2 mm宽的主斜裂缝，该裂缝与有限元分析的等效塑性应变云图结果重合。其余裂缝分布均在有限元分析结果的塑性应变范围内，说明有限元模拟结果与试验实测的裂缝分布情况较为吻合。

(a) S5模拟值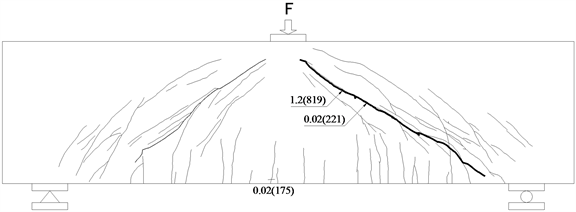(b) S5试验值

Figure 6. Comparison of S6 finite element simulation and test crack distribution

图6. S6有限元模拟与试验裂缝分布比较

3.3. 参数分析

分别对试验的6根UHPC梁将剪跨比变化为1.2、1.6、2.4、2.8、3.2进行模拟，其中剪跨比为2.4、2.8、3.2的UHPC梁采用跨中单点加载，剪跨比为1.2和1.6的采用四点对称加载，得到对应的极限荷载模拟值或试验值汇总于图7，图中剪跨比为2的是试验结果。

Figure 7. Simulation results of L1~L6 beam parameter expansion

图7. L1~L6梁参数扩展模拟结果

模拟中发现，在剪跨比为3.2时，部分梁的破坏类型已经转变为受弯破坏。在剪跨比、配箍率和UHPC钢纤维掺量三个因素综合作用下，6根模拟梁随着剪跨比从1.2增加到1.6、2、2.4、2.8，抗剪承载力相对于剪跨比为1.2的分别平均降低7%、17.6%、21.6%、29.5%；钢纤维掺量从1%变化到0.5%、1.5%和2%，抗剪承载力相对于1%的分别平均增加−36.1%、6.4%和10.8%；配箍率从0增加到0.19%和0.25%，抗剪承载力相对于配箍率为0的分别平均增加3.3%和5.9%。对比模拟数据可以看出，剪跨比是影响R-UHPC梁抗剪承载力的主要因素，钢纤维掺量和配箍率也是影响抗剪承载力的重要因素；且钢纤维掺量为0.5%与掺量为1%以上的R-UHPC梁抗剪承载力差异明显。

剪跨比为1.2~2.8的R-UHPC梁表现为明显的剪切破坏，破坏区域主要集中在剪跨区，呈由支座向加载点扩散的斜向塑性应变，受弯曲影响的竖向塑性应变主要集中在梁底部，向上扩展效果不明显。随着跨径的增大，梁的受剪破坏作用逐渐减小，受弯影响开始增大，表现为剪跨区的斜向塑性应变下移，受弯竖向塑性应变向上扩展且逐渐增大。最终在梁长为1800 mm，剪跨比为3.2时，在梁跨中位置出现一条快速向上扩展的竖向塑性应变，此时梁在弯曲作用下发生破坏，为确保模拟结果全为受剪破坏，后文关于抗剪数据的分析均考虑剪跨比在1.2~2.8范围内。模拟发现，R-UHPC梁的主斜裂缝倾角随着钢纤维掺量的增加而减小，随着配箍率的增加而增大，大部分梁的斜裂缝倾角随着剪跨比的增加而减小。

由于S1梁随着剪跨比的增加，由受剪破坏转为受弯破坏，在剪跨比为3.2时，因为破坏类型的转变，破坏裂缝成为跨中受弯竖向裂缝，主斜裂缝无法明确区分，因此为确保所有梁的破坏类型均为受剪破坏，主斜裂缝只统计剪跨比为1.2~2.8的模拟梁。将无腹筋梁S1~S4作为一组，以钢纤维掺量 ${\rho }_f$ 作为变量，统计在不同剪跨比下的斜裂缝倾角模拟结果汇总于表4：

Table 4. Inclination angle of main oblique crack under different steel fiber content

表4. 不同钢纤维掺量下的主斜裂缝倾角

将1%钢纤维掺量的梁S1、S5、S6作为一组，以配箍率 ${\rho }_{sv}$ 作为变量，统计在不同剪跨比下的斜裂缝倾角模拟结果汇总于表5：

Table 5. Inclination of main oblique fracture under different stirrup ratios

表5. 不同配箍率下的主斜裂缝倾角

4. 结论

1) 进行有限元分析时，加载位置的垫块与混凝土实体之间应设置为摩擦接触；混凝土实体的网格尺寸控制在保护层厚度的1~2倍，同时应保证REINF加强筋单元的体积比不宜过小；使用位移加载和位移收敛准则，提升计算的收敛性，更易获得混凝土梁的极限荷载和下降段；为得到结构的极限承载力，加载值在预估的极限承载能力上进行适当放大。

2) 通过有限元进行参数分析，随着剪跨比的增加，梁的受剪作用减小，受弯影响增大。剪跨比是影响R-UHPC梁抗剪承载力的主要因素，UHPC钢纤维掺量和配箍率也是影响抗剪承载力的重要因素；且钢纤维掺量为0.5%与掺量为1%以上的R-UHPC梁抗剪承载力差异明显。

3) R-UHPC梁的主斜裂缝倾角随着钢纤维掺量的增加而减小，随着配箍率的增加而增大，对斜裂缝倾角起主要影响的是剪跨比，其次是配箍率和钢纤维掺量；随着剪跨比的增加，大部分梁的斜裂缝倾角逐步减小，部分梁的主斜裂缝呈现先减小后增加的趋势。

NOTES

^*通讯作者。