软土地层深基坑悬臂式帷幕降水渗流效应研究

Study on the Seepage Effect of Dewatering for Deep Excavation with Cantilever Curtain in Soft Soil

摘要: 本文以上海地区沪通铁路太仓至四团段吴淞口长江隧道浦西接收井超深基坑工程为背景，采用ABAQUS有限元模拟软件对基坑降水渗流效应进行了研究。该基坑采用悬臂式帷幕降水方式，在承压水边界条件下，分别计算了四类降水工况，结果显示井内降水数值模拟和现场试验匹配较好，误差在可接受范围内，可为现场抽水方案的设计优化提供参考，而井外的观测井位降水数值模拟结果与实际值偏差较大。在后续的研究中，可以考虑将边界条件设置为静水压力边界对井外观测点降水进行模拟，以探究降水渗流效应对周边环境的影响。

Abstract: In this paper, ABAQUS finite element simulation software was used to study the seepage effect of dewatering for deep excavation, based on the deep excavation project for the Wu Songkou Yangtze River Tunnel on the Shanghai-Nantong Railway from Taicang to Situan in the Shanghai area. The excavation adopts the cantilever curtain method for dewatering. Under the pressure water boundary, four types of dewatering conditions were calculated. The results showed that the numerical simulation of dewatering in the well matched well with the on-site test, and the error was within an acceptable range, which could provide a reference for optimizing the design of the on-site pumping scheme. However, there was a large deviation between the simulated values and actual values of the observed wells outside the well. In future research, it is suggested to set the boundary conditions as the hydrostatic pressure boundary to simulate the dewatering of the observation wells outside the well so as to explore the effect of seepage on the surrounding environment.

1. 引言

随着我国经济的快速发展及城市化进程的加快，地上空间供需矛盾日益突出，对地下空间的开发利用已迫在眉睫，国际隧道协会于20世纪80年代提出的“大力开发地下空间，开始人类新的穴居时代”的倡议，正得到越来越多的响应 [1] 。受既有地下建筑结构影响，新建的结构埋深将越来越大。上海地区以软土地层为主，渗透系数高，在该地区进行基坑开挖等地下工程施工时应尤为注意降水问题，防止地下水渗流造成开挖面失稳、地面沉降等问题，尤其是在深埋基坑工程中，地下水问题将更加突出 [2] 。因此，本文利用三维有限元数值模拟，探究了软土地层深基坑悬臂式帷幕降水渗流效应的影响。

对于岩土工程中的基坑开挖问题，Clough [3] 首次使用有限元的方法对其进行了分析，经过30多年的发展，有限元方法已经成为分析基坑工程的主流方法之一，诸如PLAXIS、FLAC2D、FLAC3D、ABAQUS等有限元软件正被越来越多的学者应用以研究基坑工程相关问题 [4] [5] [6] ，本文选择使用ABAQUS有限元分析软件建模分析深基坑悬臂式帷幕降水渗流效应。

许多学者已针对基坑降水的有限元模拟工作开展了相关研究：游洋等 [7] 基于长江下游的某深大基坑，使用数值模拟软件建立了三维非稳定流模型，分析比较了两类降水方案的降深结果，从而确定最优降水方案。沈露等 [8] 以杭州地铁1号线过江隧道为例，建立三维渗流模型研究了深基坑开挖中遇到的承压水问题，通过多次试算得到合理降水方案。欧孝夺等 [9] 基于现场降水试验，建立三维渗流数值模型用于南宁基坑的降水模拟，预测水位降深随时间的发展规律，与实际情况吻合较好。汪鹏程等 [10] 依托某地铁车站深基坑工程，进行了三维流固耦合降水开挖数值模拟分析，研究了降水对基坑开挖时坑底隆起变形量的影响，结果显示数值模拟结果与实测值较为一致，降水开挖能有效减少基坑变形量。王晋华 [11] 基于GMS软件，建立了地下水流模型以对基坑降水进行预测分析，以减少深厚卵石地层基坑在地下水条件下开挖的风险。李曙光等 [12] 基于苏州市轨道交通S1线深基坑降水施工项目建立有限元模型，对基坑施工的安全风险进行分析，研究了降水开挖的过程中地表沉降、地下连续墙变形规律，辅助基坑开挖安全施工。陈松等 [13] 从优化深基坑降水方案出发，建立了基坑降水开挖全过程三维有限元模型，分析降水方案的可行性。结果表明优化降水方案达到了预期降水效果，基坑内水位下降一段时间后趋于稳定，且基坑围护结构的止水效果符合要求。郑宇 [14] 采用有限元方法对某地铁工程基坑降水效果进行了模拟，分析了降深和地表沉降的变化情况，并根据模拟结果提出了合理的基坑降水措施。李鹏举等 [15] 采用三维有限元软件，对某地铁车站基坑降水开挖过程进行了数值模拟，以不同的悬挂式止水帷幕深度作为变量，研究临近高铁桥墩的沉降量变化情况，并给出了保证安全的临界止水帷幕深度值以供参考。邵朝阳等 [16] 利用ABAQUS有限元软件分析止水帷幕插入深度对基坑降水开挖时水位降深的影响规律，并结合室内试验的结果，得出了止水帷幕插入比的有效值，当止水帷幕插入比不小于该有效值时，水位降深较大，止水帷幕可以充分发挥止水效果。曾凡福 [17] 使用PLAXIS有限元软件建立了三维有限元模型，分析了综合管廊基坑降水效果，研究了降水井分布间距对地下水压力、地层变形情况的影响，总结了基坑变形、基坑降水量随时间的变化规律。可以看出，大部分研究均依托于某一实际工程，对重点研究区域进行数值建模，并将模拟结果与试验对比以验证其有效性，在此基础上探究某些重要参数的变化规律。

2. 工程简介

2.1. 工程概况

沪通铁路太仓至四团段吴淞口长江隧道位于宝山区黄浦江吴淞口附近，其中浦西接收井为超深基坑工程，基坑深度37.6 m。本文以该基坑工程为背景，对降水渗流效应进行了数值模拟分析。

2.2. 工程地质条件

根据地勘报告可知，拟建场地为正常沉积区和古河道沉积区，土层变化较大，在勘探中所揭露深度100 m范围内地基土均为第四系上更新统Q3和全新统Q4沉积物，主要由淤泥质黏土、淤泥质粉质黏土、黏土、粉质黏土、粉土、砂类土组成，根据土的成因、结构和物理力学性指标综合分析，自上而下将其划分为：杂填土层、粉质黏土层、粉土层、淤泥质粉质黏土层、淤泥质黏土层、黏土层、粉质粘土层、粉土层和粉砂层。如图1所示。

Figure 1. Geologic profile of the project

图1. 工程地层剖面图

由于拟建场地基坑底部为深厚的微承压水层与承压水层，渗透系数髙，各层水力联系大，且上海地区⑧号粘性土层缺失，无法形成封闭的止水帷幕，给基坑承压水降水带来极大的难度。为了有效控制降水对周边环境带来的影响，需要合理安排降水措施，提出相应的减渗防护措施。

2.3. 降压井布置方案

根据地层特性和降水需求，基坑降压井(含备用、观测井)井结构布置方案为：

1) 坑内抽水井2口，井深69 m；

2) 坑内备用井1口，井深69 m；

3) 基坑内外观测井共计5口，井深75 m。

降压井布置平面示意图如图2所示。Y7-1井深77 m，滤管标高为−66.5~−73.5 m，同时位于(7) 2层和(9) 1层土中。Y7-2井深75 m，滤管标高为−66.5~74 m，位于(7) 2层土中。井口管壁直径均为325 mm。

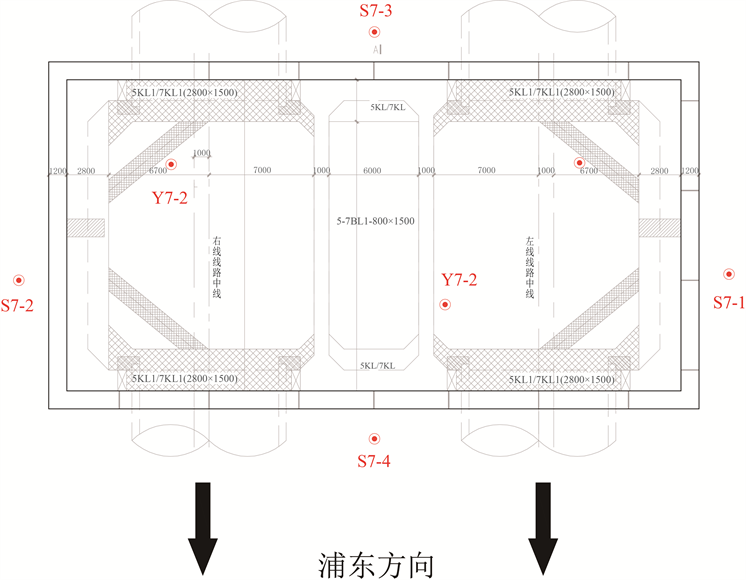
Figure 2. Layout of pressure relief wells

图2. 降压井布置平面图

3. 三维降水有限元数值模拟

3.1. 土层模型

根据地勘报告，该场地开挖范围内共存在十一种土层，各地层的参数性质如表1所示。

Table 1. Soil parameters

表1. 土层参数表

土层的物理力学性质基本参考了地质勘察报告，但勘察报告所给情况较为离散，土层平整度不高。为建模及计算方便，做了一定程度的简化，将其视作竖向成层分布的形式，且层内厚度一致。这与实际情况存在差异，但属可接受范围。

基坑外尺寸为23.2 m × 43.4 m，在此范围内降水，为消除边界效应，地连墙四侧土体应大于两倍地连墙尺寸，因此建立120 × 220 m的土体模型，并根据地连墙所在位置分割土体，如图3所示。土层部分考虑渗流作用，因此单元类型设置为C3D8P (三维8节点孔压单元)。

Figure 3. Numerical model of the soil

图3. 土层数值模型

3.2. 地连墙模型

地连墙部分采用C3D8R单元，其刚度远大于土体，在施工过程中仅出现弹性形变，故采用线弹性模型即可。其重度为26 kN/m³，弹性模量为30 GPa，泊松比为0.17。地连墙模型如图4所示。

Figure 4. Numerical model of the diaphragm wall

图4. 地连墙数值模型

3.3. 相互作用

地连墙侧壁与土体建立摩擦接触(参数见表2)，底部与土体绑定。

Table 2. Contact relationships

表2. 接触关系表

3.4. 边界条件

模型底部和四周均不允许产生法向位移，顶部为自由透水边界。

在土体不含承压水层时，土体内部孔隙水压力呈静水压力分布，忽略潮汐的影响，静水压力在最不利条件下近似于以下公式：

$P_{w0}=\gamma H$ (1)

其中： $\gamma$ 为水的重度，H为土层深度。

据此于模型四周设置孔隙水压力边界。

当土体含承压水层时，需要对孔隙水压力边界进行分段处理。在承压水层内孔隙水压力可采用静水压力与超孔隙水压力之和计算，如下式所示：

$P=\gamma H+P_{we}$ (2)

其中： $P_{we}$ 为超孔隙水压力。

3.5. 工况说明

根据降水试验，共设立四个工况如表3所示：

Table 3. Numerical simulation working conditions

表3. 数值模拟工况表

其中，抽水井点位布置如图2所示。在数值模拟中，利用指定深度的网格节点，设置确定的渗流速度，模拟真实降水管的抽水头，以期获得较为合理的渗流场。

4. 结果分析

通过对上海地区承压水层的调研，本文将承压水层，即(7)层土的水头高度设置为高于静水压力15 m (150 kPa)，并以此为基础进行相应验算。

4.1. 降水工况1

该工况对于Y7-2井点进行12 h的单井抽水，抽水量为113 m³/h。

12小时后的降水结果如图5所示，在5 (1)粘土层以下土层降水较为明显，孔隙水压力等值线围绕降水井点Y7-2下移明显。

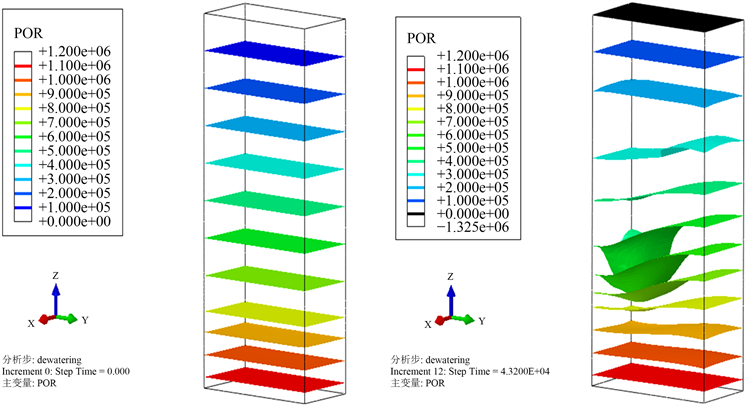(a) 初始状态 (b) 最终状态

Figure 5. Simulation result for dewatering condition 1

图5. 降水工况1模拟结果

降深对比数据如表4所示，基坑外观测井降深几乎没有变化，井内Y7-1降水数值较为匹配，说明对于井外观测点，由于承压水边界效应导致数值模拟中降水效果不明显。

Table 4. Comparison of dewatering condition 1

表4. 降水工况1对比

4.2. 降水工况2

该工况对于Y7-1井点进行12 h的单井抽水，抽水量为124 m³/h。

12小时后的降水结果如图6所示，在5 (1)粘土层以下土层降水较为明显，孔隙水压力等值线围绕降水井点Y7-1下移明显。

(a) 初始状态 (b) 最终状态

Figure 6. Simulation result for dewatering condition 2

图6. 降水工况2模拟结果

降深对比数据如表5所示。可以看出，基坑外观测井水位降深依然较小，基坑内部Y7-2降深模拟值较试验值略小，可能是由于模拟时选取的土质参数与实际情况有出入。

Table 5. Comparison of dewatering condition 2

表5. 降水工况2对比

4.3. 降水工况3

该工况对于Y7-1井点进行12 h的单井抽水，抽水量为271 m³/h，与工况2相比加大了抽水量。

12小时后的降水结果如图7所示，降深数值较工况2相比进一步增加，降水点位处出现明显负孔隙水压力，未出现负孔隙水压力土层。

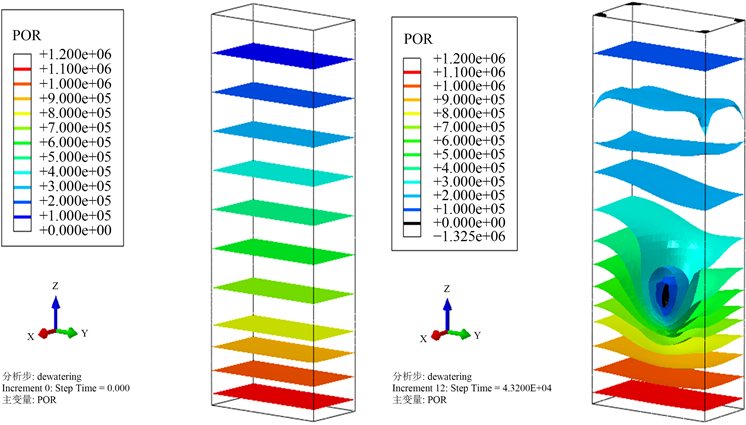(a) 初始状态 (b) 最终状态

Figure 7. Simulation result for dewatering condition 3

图7. 降水工况3模拟结果

降深数据对比如表6所示。基坑内观测井Y7-2的模拟结果与试验实测值匹配程度较高，且由于抽水量相较于工况2有了增加，Y7-2的水位降深明显加大。外部观测井则受承压水边界条件影响，数值变化较小，模拟值与实测值偏差较大。

Table 6. Comparison of dewatering condition 3

表6. 降水工况3对比

4.4. 降水工况4

该工况对于Y7-1和Y7-2井点进行24 h的双井抽水，抽水量为Y7-1井点278.5 m³/h，Y7-2井点86 m³/h。

24小时后的降水结果如图8所示，由于上部土层属淤泥质黏土层，渗透系数较小，而下部土体属粉质黏土层，其渗透系数明显大于上部土体，因此在渗流速度上存在明显差异，结果表明，该深度土层中出现显著的负孔隙水压。

(a) 初始状态 (b) 最终状态

Figure 8. Simulation result for dewatering condition 4

图8. 降水工况4模拟结果

降深对比数据如表7所示，仍然是由于承压水边界的影响，基坑外观测点位降水效果不明显，数值模拟值均小于试验实测值。

Table 7. Comparison of dewatering condition 4

表7. 降水工况4对比

5. 结论

本文以上海沪通铁路太仓至四团段吴淞口长江隧道为背景，通过三维有限元数值模拟方法研究了软土地层深基坑悬臂式帷幕降水渗流效应。共设置了4类降水工况，将三维数值模型计算结果与现场降水试验监测数据进行了对比分析，结论如下：

1) 承压水边界条件下井内降水数值模拟和现场试验匹配较好，误差在1 m水头左右，考虑到地层状况的不均匀性和受潮汐的影响，该误差在可接受范围内，且误差值均较为保守，数值模拟的结果可以为现场试验提供一定的参考价值，从而辅助降水方案的设计。

2) 井外的观测井位由于数值模拟承压水边界的边界效应，与实际值偏差较大，不具备参考价值。在后续的研究中，可以考虑将边界条件设置为静水压力边界对井外观测点降水进行模拟，以探究降水渗流效应对周边环境的影响。

NOTES

^*通讯作者。