1. 引言
我们考虑如下在
中的常系数不可压缩磁流体(MHD)系统的局部适定性问题:
(1.1)
其中u表示速度场, 表示磁场,
表示压强。正常数
分别表示粘性系数和磁扩散系数。本文为了方便起见,令
。
磁流体系统是用来研究磁流体动力学运动的经典系统,可以用来模拟太阳风、磁暴等磁流体现象,也可以用来研究宇宙中的磁场结构和磁流体运动,它在物理学、工程学中扮演着重要的角色。
当b = 0时,方程退化为经典的Navier-Stokes系统,对该系统的一个重要观测是以下标度不变性:
(1.2)
我们强调临界空间指的是其范数在(1.2)的放缩下保持不变的空间。Fujita和Kato [1] 在临界齐次Sobolev空间
中证明了Navier-Stokes系统解的全局适定性,Cannone在 [2] 中证明了当
时在
空间中的适定性,Chemin [3] 在
中证明了解的存在唯一性。基于对Navier-Stokes系统研究的理论方法,学者们进一步展开对MHD系统的系列研究,近年来,由于MHD模型的良好的对称性,已有很多关于解的适定性,弱解正则性以及解的渐进性为的研究,在临界空间中,Hao [4] 证明了
时可压缩粘性磁流体动力学(MHD)系统在整个
空间中的Cauchy问题。后来,Bian和Yuan [5] 证明了可压磁流体力学方程在临界Besov空间对于初值满足
,
,
,
的局部适定性,其中H表示磁场。近来,也有许多学者研究了可压MHD方程关于小初值强解适定性以及大初值的适定性问题,具体可参见 [6] [7] [8] 。
主要结论如下。
2. 主要定理
定理2.1 令
,
且
,则存在
,使得当
时,方程(1.1)有唯一解
.
3. 预备知识
在给出主要定理之前,我们首先回顾 [9] 中关于Littlewood-Paley理论 [9] 的一些基本定义。对于
,
设
,
,
,其中
是光滑函数,使得
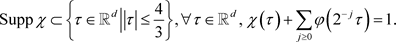
我们记算子
,
。
下面给出齐次Besov空间的定义。
定义3.1 设
,
。我们考虑
,表示
且满足
,齐次Besov空间的范数为:
定义3.2 (a) 给定一个Banach空间,我们记
。
(b) 对于
,记号
表示I上取值于X的可测函数的集合,使得
属于
。当
时,记
。
引理3.1 令
,且
。对于
,我们有
(3.1)
引理3.2 令
,且
。令u为如下热方程的解
记
。则存在常数c,
使得
(3.2)
特别地,有以下估计
. (3.3)
引理3.3 (插值不等式)对于
,
,且
,有以下插值不等式成立
(3.4)
其中
,
.
引理3.3 (Bernstein不等式)令B为
中的球,
为
中的一环,令
,则
(3.5)
4. 主要定理证明
由于
的不可压性质,我们有
,对方程(1.1)作用
得
下面,我们利用逼似解 [10] 的论证过程来证明这一结果。令
为如下方程的解
(4.1)
构造
,
是如下线性方程组的解:
(4.2)
4.1. 逼近解列的一致有界性
令
,
,
且
,则存
在足够小的
,使得解
和解
满足
其中
,
。
证明:对于方程(4.1),我们利用引理3.2中(3.2)式易得
,利用引理3.2中(3.3)式得
,
对
,取
,存在
,使得
从而证得
。
下用归纳法证明
,对方程(4.2)运用引理3.2中(3.2)式得
(4.3)
(4.4)
对于(4.3)式的第一项,我们应用引理3.1和插值不等式得
对于(4.4)式的第一项,在引理3.1,young不等式和插值不等式的帮助下,得
取
足够小使得
,类似地,我们可以得到
和
的
估计。综合(4.3)和(4.4)的估计完成了
的证明。
4.2. 解的存在性和唯一性
为了得到局部解的时间存在性,我们将证明
是如下空间的Cauchy序列,即
对
,
足够小,设
则有如下系统
(4.5)
其中
对任意
,因为
,由引理3.1和3.2,这里令
,有
(4.6)
由Bernstein不等式得
(4.7)
结合(4.6)和(4.7)得
,
其中常数
,取
足够小使得
,可得
在
中为一收敛序列。从(4.1)和(4.2)中可以找到极限
是初值满足
的方程组(1.1)的解,且
。
类似于解的局部存在性证明,可以得到解
的唯一性。因此,我们完成了解
在
上存在唯一性的证明。
5. 总结
本文针对方程(1.1),采用构造逼近解列的方法 [10] ,通过Cauchy列收敛证明该逼近解有极限,然后利用极限唯一性证得逼近解在分布意义下是方程(1.1)在
上的解,进而证得该解也是唯一的。由于MHD方程良好的对称性及其在物理学上的重要性,我们认为对MHD系统的解的性质的研究是非常重要的。基于对Navier-Stokes方程组的学习,我们对MHD中的线性系统以及非线性的处理,可以从Navier- Stokes方程组运用到的一些方法中借鉴或汲取灵感,提高研究的可行性。之后我们可以进一步研究临界齐次空间解的整体适定性以及非齐次不可压MHD方程组的整体适定性问题。