1. 引言
静脉曲张常用的理疗方法是压迫治疗法,患者通过穿戴医用压力袜促使腿部血液正常回流到心脏。医用压力袜的设计需要遵循严苛的标准 [1] ,如何根据静脉曲张患者不同的腿部形状快速定制合身的压力袜是保证治疗效果的重要研究课题。考虑到CAD/CAM技术在制造业发挥出的巨大作用,可以对人体腿型进行参数化建模,进而配合生产标准付诸制造。这就要求模型应能够实现小腿形状的高精度重建。
曲面重建主要分为两个步骤,首先采用三维扫描仪获取表面点云,然后进行曲面拟合。后者通常使用非均匀有理B样条(Non Uniform Rational B-Spline, NURBS),因其对自由型曲面精确的表达能力及灵活性而被国际标准化组织(International Organization for Standardization, ISO)定义为描述工业产品几何形状的唯一标准。曲面拟合可以通过插值和逼近两种方法实现。在基于点云的曲面重建中,由于数据点不是精确给定的,因此通常采用逼近的方法。其中,节点矢量的选择直接决定了曲面重建的质量,而节点优化的高维非线性和非凸性使其成为了NURBS曲线曲面逼近中最具有挑战性的难题。Piegl和Tiller [2] 通过计算输入点参数平均值来确定节点的位置(New Knot Placement Method, NKTP),该方法使得数据点在节点空间按照弦长均匀分布并且可以得到稳定的方程组。当数据点特征丰富含有不连续点或者尖突时,NKTP技术表现欠佳。对于此,一种解决思路是使用启发式方法,即通过分析数据点的几何特征如曲率从而获取粗略的节点位置,随后利用节点插入算法来细化节点矢量使逼近曲线满足给定的公差 [3] [4] [5] [6] [7] 。Park和Lee [3] 提出了一种基于所谓主导点的节点配置方法,将曲线拟合转化为了主导点选择的问题,使用插入算法增加主导点的数量直到逼近曲线满足给定的误差边界。Tjahjowidodo等人 [4] 使用二分法选取最佳的分段线性函数来拟合数据点的二阶导数从而确定节点矢量。随后,Dung和Tjahjowidodo [5] 又提出了一种快速计算最佳节点的两步法:先用二分法对数据点进行分割以得到粗略的节点,而后采用非线性最小二乘技术优化节点的位置以及连续性水平。另外一种节点配置的思路是从一个密集的节点矢量开始,在满足给定的基准下尽可能地去除冗余的节点。这里有一些文献提出的节点配置方法是基于此思路的 [8] [9] [10] 。
除了前述传统的节点配置方法以外,Laube 等人 [11] 将支持向量机运用到节点矢量选择上来。紧接着,他们又提出两个深度学习网络模型——数据点参数化网络和节点矢量选择网络,分别用来进行数据点的参数化和节点优化 [12] 。虽然这两种机器学习方法取得了不错的效果,但是由于其需要特定的数据集作为支撑,因而不能广泛应用。
另一方面,有许多文献也将随机搜索方法用于节点矢量优化。元启发式算法如萤火虫算法 [13] 、粒子群算法 [14] [15] 、人工免疫系统 [16] 和大爆炸算法 [17] 等在复杂的非线性和非凸优化问题上具有天然的优势,这些文献提出的方法应用在节点配置甚至是B样条中所有参数的优化都取得了很好的效果。本文就利用粒子群算法解决了小腿曲面重建中的节点配置问题。相较于传统方法的优势在于,本文提出的方法直接为一组截面曲线和控制曲线选择统一的节点矢量,从而避免了曲线相容过程造成的巨量控制点问题。另外,本文给出了一个适应度函数来评估节点位置的优劣,以此为依据进行节点矢量的选择。最终搜索出的节点矢量使小腿曲面建模精度有了很大的提升。
2. 方法
2.1. NURBS曲线曲面方程
NURBS曲线方程是关于参数u的有理多项式矢函数,一条k次NURBS曲线有如下定义:
(1)
其中
为曲线的控制点;
是对应于每个控制点的权因子;
是一组B样条基函数,其定义在非递减序列称为节点矢量
上,可以由de Boor-Cox递推公式
(2)
计算得到。此外,在节点矢量U上,曲线有定义域
。
在实际应用中,通常将NURBS转化为方便计算机处理的齐次坐标表示形式:
(3)
其中,
为带权控制点,将所有权因子置为1,则得到非有理B样条的齐次坐标表示。
NURBS曲面是曲线张量积形式的推广,一张
次的NURBS曲面齐次坐标表达式为:
(4)
它的基函数分别由两个方向上的节点矢量
和
定义。曲面定义域为
。
2.2. 曲面逼近
首先介绍NURBS曲线逼近方案,曲面逼近可以容易地由此推广得到。
NURBS曲线逼近问题可以描述为:给定具有
个控制点的k次NURBS曲线
,其表达式如式(1)所示,节点矢量已知,求其控制点使曲线在
处尽可能逼近数据点
。这是一个线性最小二乘问题,有损失函数:
(5)
其矩阵表示形式:
(6)
式中,
和Q分别为控制点和数据点组成的矩阵
,
,N是由B样条基函数组成的
阶矩阵:
要使
取得最小值,则对式(6)求导,令导数为0,于是得到方程组:
(7)
求解之则得到曲线的控制点
。
上述给出了一般意义的NURBS曲线逼近方案,然而,实际应用中通常使曲线插值于首末数据点,并且采用固支条件的NURBS曲线,即具有节点矢量
此时曲线也插值于首末控制点,因此方程组7中的
可以直接得出。
NURBS曲面逼近问题即给定
次NURBS曲面
,其表达式如式(3),具有网格控制点
。节点矢量U,V已知,求解控制点使该曲面在参数对
处逼近网格点
。
曲面重建可以由两阶段地重复使用曲线逼近来完成。首先,对网格点的每一列即u方向上分别进行曲线逼近得到一组等参数线
和控制网格
;然后对上一步得到的控制网格的每一行分别进行
个控制点的l次曲线逼近,最终便得到所求的曲面控制网格
。
2.3. 基于粒子群算法的节点配置方法
上节中介绍了线性的曲线、曲面逼近方法,实际上在小腿曲面建模过程中仅有数据点是给定的,而模型的超参数即控制网格的维度、曲面的阶次、节点矢量以及数据点的参数都是未知量。因此,完整的曲面重建过程一般需要两个步骤,第一步确定模型的上述超参量,第二步进行最小二乘曲面逼近。控制点数目和曲面阶次一般根据经验通过照看的方式确定;而数据点的参数化一般通过考察数据点按弦长的分布情况即弦长参数化方法得到。节点矢量直接决定了曲面模型的基函数,从而影响到曲面重建的质量。虽然有学者如Piegl [2] 、施法中 [18] 等已经给出节点配置的一般方案,但是针对具体的曲线、曲面重建问题其具有一定的优化空间。
元启发式算法非常适合解决节点配置这种高维非线性和非凸优化问题 [13] [14] [15] [16] [17] ,本文就采用粒子群算法 [19] [20] (Particle Swarm Optimization, PSO)实现小腿曲面重构中的节点配置。粒子群算法原理不再赘述,首先初始化一群粒子,每个粒子代表问题的一个特定解,同时设定一个适应度函数来评价当前粒子位置的优劣。粒子有位置和速度更新公式:
(8)
(9)
式中,
,n为粒子总数,
、
分别为粒子当前的位置和速度,
和
分别为目前个体和种群的最优解。w为惯性权重,
、
分别为个体学习因子和社会学习因子,
、
为随机因子。其中,两个学习因子一般都取2,惯性权重一般取0.9~1.2 [20] 。本文在小腿曲面重建中选用线性递减的惯性权重——早期较大的惯性权重能增强算法的全局搜索能力,算法后期减小惯性权重从而使算法快速收敛。
用粒子群算法优化节点矢量实现小腿曲面重建的步骤如算法一所示。
算法中,有几点需要着重介绍。首先在对粒子群进行初始化时,每个粒子的位置分为两部分,分别代表节点矢量U和V的定义域内节点(去掉定义域端节点)即
和
。节点矢量的其他部分为固定值,节点值限制在0到1之间,采取随机初始化策略。与之对应的,计算粒子的适应度时,首先要对粒子进行解码得到节点矢量,方法是取出粒子中U和V对应的节点段升序排序后作为曲面定义域内节点。然后对于节点U,由于要在u向上拟合NURBS闭曲线,定义域外节点通过对定义域节点做周期性延展得到。对于节点V,定义域外的节点直接采取固支条件取l重端节点。
粒子群优化的核心是确定合适的适应度函数来评估粒子的适应度。在节点矢量优化任务中,可以采用曲面逼近误差来衡量节点矢量的优劣。对于NURBS曲面拟合误差,本文给出如下定义:
(10)
其中
如式(10)所示,曲面拟合误差定义为两个方向上曲线拟合误差的加权平均值,而后者分别为截面曲线和控制曲线拟合误差的均值。曲线拟合误差采用均方损失。由于截面曲线的拟合效果直接决定曲面重建的精度,因此
应取较大权重,本文在小腿曲面建模中
设置为0.8,则
为0.2。
3. 实验
3.1. 点云预处理
人体腿部三维点云如图1(a)所示,首先应用主成分分析(Principal Components Analysis, PCA)得到点云的走势后将腿旋转放正,如图1(b)所示。
 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 1. Point cloud pre-processing process
图1. 腿部点云预处理过程示意图
原点云的数据量庞大,点的分布无序散乱,并且含有噪声点,需要对其筛检重构得到有序均匀排布的网格点。首先用一组水平面对点云进行重采样得到小腿截面点云,如图1(c)所示。然后对每个截面进行高精度的NURBS曲线逼近,接着用等间隔的弧度序列对拟合出的截面曲线进行采样。最后就得到了不同截面间分布均匀的网格点,如图1(d)所示。
3.2. 小腿曲面重建
预处理点云得到网格点后,就可以利用算法1进行小腿曲面重建。选择双三次NURBS曲面,使用弦长参数化方法对数据点进行参数化,经过试验后选择合适的控制点数目为20 × 16。另外,粒子群算法中的种群大小和迭代次数分别为50和100。采取线性递减的惯性权重,初始值与终值分别设置为1.2和0.4。实验全部在Windows 10操作系统下使用MATLAB R2018a完成。
如图2所示为算法迭代过程中粒子群的平均适应度以及种群历史最好个体适应度的变化情况。从图中可见,算法早期由于粒子具有较大的惯性速度,平均适应度曲线具有较大的波动,这有利于粒子全局寻找最优解。到迭代后期,粒子的惯性权重降低,算法逐渐收敛。选取粒子群最优的个体解码得到节点矢量U,V,然后对小腿进行曲面重建,过程如图3所示。图3(a)为曲面逼近的第一阶段即小腿截面曲线的拟合;图3(b)为曲面逼近第二阶段得到的控制曲线;图3(c)为重建后的小腿NURBS曲面,图3(d)直观展示了重建曲面与原点云的逼近效果。
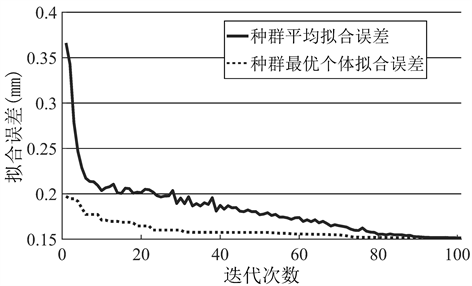
Figure 2. Fitness variation curve of particle swarm optimization
图2. 粒子群的适应度变化曲线
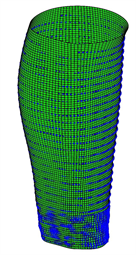
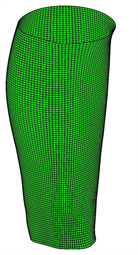

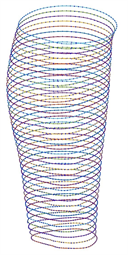 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 3. Reconstruction process of calf surface
图3. 小腿曲面重建过程
3.3. 误差分析
在对建模精度进行量化评估时,需要计算点云到重建曲面的距离。考虑到直接求点到NURBS曲面的距离计算开销较大,对此本文采用一种近似的方法:将NURBS曲面近似为四边形网格面,当网格的密度足够大时就可以将点到网格面的距离近似为到NURBS曲面的距离。用此方法得出的小腿不同高度位置的曲面重建误差如图4所示。可见,重构曲面与点云的误差稳定在0.3 mm左右,脚踝附近误差相对较大,这是由于此处腿部曲面曲率变化较大,细节丰富,并且在对点云进行重构时也会丢失部分特征信息。曲面重建平均误差约为0.29 mm,相比前人工作降低近70% [21] 。
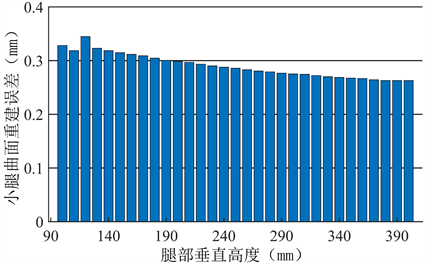
Figure 4. Surface reconstruction error of the calf
图4. 小腿曲面重建误差
最后,采取不同的控制点数量,分别用NKTP [2] 节点配置方法和算法1 (称作PSOKP)进行小腿曲面重建,两者的重建精度对比如表1所示。不难得出,在控制点数目相当时,本文提出的基于PSO的节点配置技术相较于NKTP,小腿曲面重建误差平均降低了10%。从另一方面来讲,在保持相当的拟合精度时,本文的算法得到的NURBS曲面控制点数目相较于NKTP最高能减少49%。这是很有利的因为较大的控制点数量不仅不便于计算、存储,并且会降低NURBS曲面的光顺性。

Table 1. Accuracy of calf surface reconstruction with different number of control points (mm)
表1. 不同数目控制点小腿曲面重建精度(mm)
4. 结语
本文提出了一种参数化建模方法,对腿部点云进行了小腿曲面高精度重建,并使用粒子群算法优化NURBS曲面节点矢量的配置,极大地提高了建模精度。在保证良好的光顺性前提下,重建曲面与原点云误差低至0.29 mm。本文方法和技术不仅可以应用于压力袜的精准、快速定制化,也对其他压力服的个性化设计制造提供了重要的参考。
NOTES
*通讯作者。