1. 引言
本文我们考虑了在
空间中微极流体方程的局部适定性问题:
(1.1)
其中
表示流体的速度,
表示流体的为旋转速度,
表示压力,
为
常粘性系数。在本文中,为方便起见,令
,
。
微极流方程于1966年首次由C. A. Eringen [1] 引入,用于模拟微极流体。它可以看作是一种非牛顿流体,具有微旋转效应和微转动惯量。微极流体是具有微观结构的流体,涵盖了许多现象(如由悬浮在粘性介质中的颗粒所组成的流体等),是Navier-Stokes方程的重要推广。
当
和
时,系统(1.1)退化为经典的Navier-Stokes方程。Navier-Stokes方程有以下的尺度不变性:
(1.2)
而临界空间是指对于尺度变换保持空间范数不变的空间。
对于Navier-Stokes方程适定性的研究已有大量的文献。对于临界空间,Fujita和Kato [2] 得到了
Navier-Stokes方程在临界齐次Sobolev空间
中的全局适定性结果。Cannone [3] 证明了Navier-Stokes
方程当
时初值在
空间中的适定性;Chemin [4] 推广了Cannone的结果,研究了初值在
中Navier-Stokes 方程的适定性。
对于不可压缩微极流方程,Chen和Miao [5] 证明了三维不可压缩微极系统对于小初值在
中的整体适定性。Song受到Chemin [4] 的启发,在 [6] 中推广了Chen [5] 的结果,将
的范围从
,
分别扩展到
,
,得到了更一般的全局适定性。另外,关于具有全粘性和部分粘性的二维不可压缩微极系统的适定性可以参考 [7] [8] 。
对(1.1)1作用Leray投影算子
,可得
(1.3)
其中
,
且由
易知
。
显然,这个系统相较于Navier-Stokes方程已不满足尺度不变性。而处理微极流方程的困难主要在于处理方程中的耦合项
,我们利用Qian等人在 [9] 中的技巧,可在
能量方法中将(1.3)中的
与
相抵消。
在本文中,对于给定的Banach空间X,我们记
。对于
,记号
表示I上取值于X的可测函数的集合,使得
属于
。当
时,记
。
主要结论如下。
2. 主要定理
定理2.1令
,则存在
使得系统(1.1)有一个局部且唯一的解
。
3. 预备知识
首先回顾齐次Besov空间的定义。
定义3.1 [10] 令
,
,齐次Besov空间是由分布
(即
且满足
)所组成的,且有
引理3.1 [11] 令
,
,
,
。令u是热方程(3.1)的解
(3.1)
记
,则存在两个依赖于维数d的正常数c和C使得
(3.2)
特别地,有以下估计成立
(3.3)
注3.2通过类似于引理3.1的证明过程,对于线性热方程
(3.4)
的解也有估计式(3.2)成立.
引理3.3 [12] 令
,
,
且
。对于
,我们有
(3.5)
引理3.4 [10] 对于
,
,且
,有以下插值不等式成立:
(3.6)
其中
,
。
4. 定理证明
4.1. 构造逼近解列
首先,构造(1.3)的逼近解列
。
令
是以下方程组的解:
(4.1)
其中
,
。
令
,
且
是以下线性系统的解:
(4.2)
4.2. 逼近解列的一致有界性
先对
进行估计,对(4.1)1作用
,
再对上式两端乘以
并在
上积分,利用Young不等式可得
(4.3)
同理有
(4.4)
将(4.3)和(4.4)相加,利用Bernstein不等式得到
则有
对上式在
上积分,再乘以
并对
求和即得
(4.5)
又由引理3.1
(4.6)
由于
,将
的方程(4.1)2分解为
(4.7)
易知
,则对(4.7)1和(4.7)2分别运用引理3.1、注3.2,再由
的性质可得
(4.8)
根据
的估计(4.5) (4.6)和(4.8),我们可选取一个时间
使得对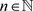 ,有以下不等式成立:
,有以下不等式成立:
(4.9)
其中
,
。
对于
,我们运用归纳法证明以下估计成立
(4.10)
假设(4.10)成立,则下证(4.10)对于
成立。
通过类似于(4.5)式的估计过程可得
(4.11)
对于上式右端两项,利用引理3.3、引理3.4以及(4.9)和(4.10)有
(4.12)
(4.13)
将(4.12)和(4.13)代入(4.11),并取
足够小,使得
,即得
(4.14)
因此,(4.10)对于
成立。
4.3. 解的存在性和唯一性
下证:对于所有的
,
足够小,
为空间
中的柯西序列。
令
,
,
,
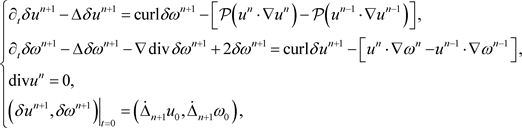 (4.15)
(4.15)
对任意的
,记
。
分别将算子
作用于方程(4.15)2,对(4.15)2分解后的两个方程以及(4.15)1分别运用引理3.1、注3.2,再相加得到
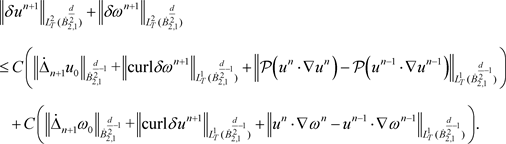 (4.16)
(4.16)
下面对上式右端项进行估计:
由Bernstein不等式、Holder不等式以及引理3.3,可得
(4.17)
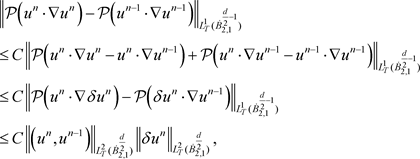 (4.18)
(4.18)
(4.19)
(4.20)
记
,我们知道初值
,由此可得当
时,
。通过(4.9)和(4.10)以及引理3.4,易知
是有界的。结合(4.16)~(4.20),我们得到对任
意的
,
(4.21)
其中
是一个常数。取
使得
,
,则
(4.22)
这表明序列
在
中收敛。结合(4.1)和(4.2),可得极限
是系统(1.3)对于初值
的解且
(4.23)
类似于解局部存在的证明过程,可以得到解
的唯一性。
5. 总结
微极流方程又称非对称流方程,由于微极流系统中耦合项的存在,使得对该系统的处理存在一定困难,对于微极流系统适定性的研究也有待完善。本文研究了
维不可压缩微极流方程在
框架下的临界Besov空间中的局部适定性,主要借鉴 [13] 的方法。首先构造逼近解列,证明逼近解列一致有界后,再通过证明逼近解列在解空间中为柯西序列,得到极限存在,随后证明该极限在分布的意义下为方程(1.3)的解,从而完成了存在性的证明。唯一性可由类似于柯西列的证明过程得到。本文的创新点在于在证明逼近解列一致有界的过程中,利用Qian等人在 [9] 中的技巧,可在使用
能量方法时将(1.3)中的
与
相抵消,相较于 [5] 中运用Green矩阵的方法更为简便,当然本文这种方法只适用于
框架。