基于SEIAQR动力学模型的突发疫情预测

Forecast of Sudden Epidemic Based on SEIAQR Dynamic Model

摘要: 科学的预测传染病的发展规律对疫情防控至关重要。本文在经典的SEIR模型的基础上考虑到无症状感染者和隔离措施，提出SEIAQR动力学模型，且潜伏者和无症状感染者均具有传染性。基于第二代再生矩阵的方法计算基本再生数R0的表达式，并进行了灵敏度分析。数据拟合结果表明，SEIAQR模型预测结果与真实数据比较吻合，可以较好地描述疫情的早期传播规律。最后，根据参数敏感性分析结果为突发疫情防控提出了合理建议。

Abstract: Scientific prediction of the development trend of infectious diseases is essential for epidemic pre-vention and control. In this paper, we consider a SEIAQR dynamic model with asymptomatic in-fected persons and isolation chambers, and both the latent and asymptomatic infected persons are infectious. The expression of basic regeneration number is calculated based on the second genera-tion regeneration matrix method, and the sensitivity analysis is carried out. The data fitting results showed that the prediction results of SEIAQR model are in good agreement with the real data and can better describe the early transmission law of the epidemic. Finally, according to the results of parameter sensitivity analysis, some suggestions for epidemic prevention and control were put forward.

1. 背景介绍

回顾COVID-19疫情已经持续了两年多，给世界人民带来了沉重的灾难。特别是奥密克戎变异株传入我国以来，我国疫情呈现出点多、面广、频发的特点 [1] ，轻症和无症状感染者比例比较高，多个地区发生局部性聚集性疫情，甚至发生学校聚集性疫情，比如杭州、吉林、上海、郑州等地相继出现的新冠疫情。COVID-19爆发以来，各个领域研究者积极对新冠疫情数据进行研究分析，包括：流行病学方法、机器学习方法、建立传染病微分方程模型等。其中，传染病动力学模型由于能形象的揭示疫情的传播机制而深受大家喜欢，SIR，SEIR以及改进的SEIR模型被广泛建立，其中以SEIR模型最为普遍 [2] [3] [4] [5] 。然而，模型却没有考虑到无症状感染者对疫情传播的影响 [6] 。

由于疫情错综复杂，导致很多模型预测不够准确，总结原因存在以下几点局限性：1) 模型简单；现有研究难以全面考虑疫情发展与防控中的部分重要因素，比如：核酸检测和隔离手段；2) 病毒的不断变异，存在大量的无症状感染者；3) 模型参数的不断变化；随着疫情发展和各种措施实行，模型参数在不断发生变化。上海疫情自3月初被发现到持续爆发就是因为存在大量的无症状感染者，隐藏了传播途径、导致未能及时发现，采取防控措施。因此，本文我们在SEIR模型的基础上考虑到存在大部分无症状感染者和核酸检测等隔离措施，建立一类参数服从指数分布的SEIAQR模型，且潜伏期和隐性感染者均具有传染性，并将模型应用到上海疫情的追踪预测中，为以后可能的突发疫情提供防控经验。

2. SEIAQR动力学模型建立

我们将疫情期间总人口划分为六个不同的仓室：易感者(S)、潜伏期患者(E)、无症状感染者(A)、显性感染者(I)、隔离确诊治疗者(Q)和移出者(R)。其中，移出者人数 = 恢复者人数 + 死亡人数 + 隔离的无症状人数。在建立模型之前，我们做出如下假设：

1) 人群种类均匀混合，不考虑人群的大规模迁入和迁出。且短期内，不考虑人口的自然出生和死亡率。

2) 人群普遍具有易感性，且只考虑人传人的传播方式。

3) 具有潜伏期，且潜伏期具有一定的传染性。

4) 具有比例为 $1-p$ 的无症状感染者，且无症状感染者具有传染性。

5) 感染者I和无症状感染者A一旦被发现隔离，视为无感染他人的能力。

6) 恢复者短期内不再考虑成为易感人群。

图1. 带无症状感染者和隔离仓室的SEIAQR模型

上述模型结构(图1)用数学模型表示为：

$\{\begin{array}{l}\frac{\text{d}S}{\text{d}t}=\frac{-c\beta S\left[\sigma E+\eta A+I\right]}{N},\\ \frac{\text{d}E}{\text{d}t}=\frac{c\beta S\left[\sigma E+\eta A+I\right]}{N}-\omega E,\\ \frac{\text{d}A}{\text{d}t}=\left(1-p\right)\omega E-\left({\gamma }_1+q_1\right)A,\\ \frac{\text{d}I}{\text{d}t}=p\omega E-\left({\gamma }_2+q_2\right)I,\\ \frac{\text{d}Q}{\text{d}t}=q_{2}I-\kappa {\gamma }_{3}Q,\\ \frac{\text{d}R}{\text{d}t}=\left({\gamma }_1+q_1\right)A+{\gamma }_{2}I+\kappa {\gamma }_{3}Q,\end{array}$ (1)

其中，c是潜伏者、无症状感染者、感染者每天接触易感者的平均人数， $\beta$ 是感染者的传染概率， $\sigma$ 是潜伏期患者传染概率衰减因子、 $\eta$ 是无症状感染者传染概率衰减因子、 $\omega$ 是潜伏者转化为感染者的速率， $q_1$ 是无症状感染者被隔离的比例， $q_2$ 是感染者被确诊隔离的比例，p是显性感染者所占的比例， ${\gamma }_1$ 是无症状感染者的恢复速率， ${\gamma }_2$ 是显性感染者的恢复速率， ${\gamma }_3$ 是确诊治疗者的移出速率。移出速率定义如下：

$\kappa \left(t\right)=1-\frac{{\kappa }_m}{1+a{\text{e}}^{b\left(t-1\right)}},$ (2)

其中， ${\kappa }_m$ 是当前条件下确诊患者的最大恢复率，a是指数增长系数，b是恢复指数递增速率。

3. 基本再生数表达式

系统(1)的前五个方程不依赖于第六个方程，因此我们只需要研究下列子系统 [7] ：

$\{\begin{array}{l}\frac{\text{d}S}{\text{d}t}=\frac{-c\beta S\left[\sigma E+\eta A+I\right]}{N},\\ \frac{\text{d}E}{\text{d}t}=\frac{c\beta S\left[\sigma E+\eta A+I\right]}{N}-\omega E,\\ \frac{\text{d}A}{\text{d}t}=\left(1-p\right)\omega E-\left({\gamma }_1+q_1\right)A,\\ \frac{\text{d}I}{\text{d}t}=p\omega E-\left({\gamma }_2+q_2\right)I,\\ \frac{\text{d}Q}{\text{d}t}=q_{2}I-\kappa {\gamma }_{3}Q,\end{array}$ (3)

令 $x={\left(E,A,I,Q,S\right)}^{\text{T}}$ ，则模型(3)可以改写为：

$\frac{\text{d}x}{\text{d}t}=F\left(x\right)-V(\; x\; )$

其中，

$F\left(x\right)=\left(\begin{array}{c}\frac{c\beta S\left(\sigma E+\eta A+I\right)}{N}\\ 0\\ 0\\ 0\\ 0\end{array}\right),V\left(x\right)=\left(\begin{array}{c}\omega E\\ -\left(1-P\right)\omega E+\left({\gamma }_1+q_1\right)A\\ -P\omega E+\left({\gamma }_2+q_2\right)I\\ -q_{2}I+\kappa {\gamma }_{3}Q\\ \frac{c\beta S\left(\sigma E+\eta A+I\right)}{N}\end{array}\right)$

分别计算 $F\left(x\right),V\left(x\right)$ 关于 $x={\left(E,A,I,Q,S\right)}^{\text{T}}$ 的全导数得：

$F=\left(\begin{array}{ccccc}\frac{c\beta \sigma S}{N}& \frac{c\beta \eta S}{N}& \frac{c\beta S}{N}& 0& \frac{c\beta \left(\sigma E+\eta A+I\right)}{N}\\ & & 0& & \\ & & 0& & \\ & & 0& & \\ & & 0& & \end{array}\right),$

$V=\left(\begin{array}{ccccc}\omega & 0& 0& 0& 0\\ -\left(1-P\right)\omega & {\gamma }_1+q_1& 0& 0& 0\\ -P\omega & 0& {\gamma }_2+q_2& 0& 0\\ 0& 0& -q_2& \kappa {\gamma }_3& 0\\ \frac{c\beta \sigma S}{N}& \frac{c\beta \eta S}{N}& \frac{c\beta S}{N}& 0& \frac{c\beta \left(\sigma E+\eta A+I\right)}{N}\end{array}\right),$

则由下一代再生矩阵可得基本再生数表达式：

$R_0=\rho \left({F{V}^{-1}|}_{E_0}\right)=c\beta \left\{\frac{\sigma }{\omega }+\frac{\eta \left(1-p\right)}{{\gamma }_1+q_1}+\frac{p}{{\gamma }_2+q_2}\right\}.$ (4)

4. 实例分析

4.1. 数据来源

疫情数据来自于国家卫健委、中国疾病控制预防中心发布的每日疫情信息，收集整理得到2022年3月 19日至4月18日上海的新冠肺炎每日新增确诊患者人数、新增无症状感染者人数、现存感染人数、累积感染人数、累计治愈病例数及死亡病例数。人口学数据来自国家统计局公布的2021年年底上海市总人口数据。

4.2. 参数估计

首先，通过查阅大量文献资料获得一致的参数赋值：c， $\sigma$ ， $\eta$ ， $\omega$ ， ${\gamma }_1$ ， ${\gamma }_2$ ， ${\gamma }_3$ 。接着，基于2022年3月19日~4月18日官网公布的每日治愈病人总数、累计死亡病例数和累计确诊人数，得到治愈率和死亡率数据。根据提出的指数型模型(2)，进行数据拟合，利用最小二乘法求得模型中未知参数 $a=18,$ $b=-0.14$ 。

因此得到确诊治疗病人移出率函数模型表达式： $\kappa \left(t\right)=1-\frac{0.93}{1+18{\text{e}}^{-0.14\left(t-1\right)}}$ ，数据拟合结果见图2。

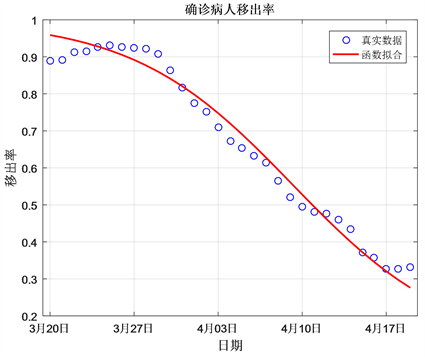
Figure 2. Fitting of the removal rate function of confirmed cases

图2. 确诊病例移除率函数拟合

未知参数 $\beta ,q_1$ 和 $q_2$ 需要通过借助Berkeley Madonna和Matlab软件，采用最小二乘算法进行求解

$\underset{c,\omega ,\beta ,q_1,q_2,\gamma }{\min }\Vert I\left(c,\omega ,\beta ,q_1,q_2,\gamma \right)-I_{实际}\Vert$

另外，模型中含有6个初值变量，分别为易感者S(0)、潜伏者E(0)、无症状感染者A(0)、显性感染者I(0)、隔离确诊患者Q(0)、移出者R(0)。其中，初值S(0)，A(0)，I(0)，R(0)和Q(0)可以由真实疫情数据得到，E(0)由后两天新增确诊病例数和新增无症状感染数据得到。具体参数估计结果见表1。

Table 1. Meaning and estimated value of parameters in the model

表1. 模型中参数含义以及估计值

4.3. 数据拟合结果

借助MATLAB软件数据拟合做出每日新增确诊人数、新增无症状感染人数、现存确诊人数和累计移出人数的模型预测值与真实数据对比效果图，见图3。

其中，预测累计移出人数=恢复人数+死亡人数。从图3中可以看出，SEIAQR模型预测结果与真实数据比较吻合，可以较好地描述上海疫情的早期传播规律。特别是，现存确诊人数与累计移出人数预测误差较小。

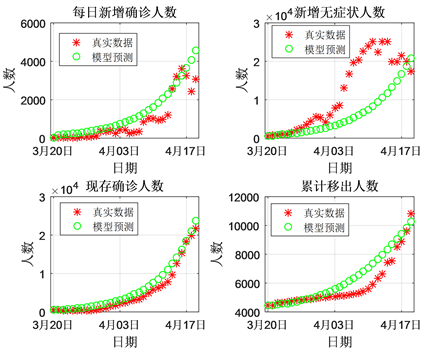
Figure 3. Fitting results of daily new confirmed cases, new asymptomatic infections, existing confirmed cases, and accumulated transfers in Shanghai from March 19 to April 18, 2022

图3. 上海2022年3月19日~4月18日每日新增确诊人数、新增无症状感染人数、现存确诊人数、累计移出人数数据拟合结果

此外，我们也做出了累计确诊病例数预测结果与实际数据对照图，见图4。从图中可以看出，预测结果比真实数据稍微偏大，可能原因是真实数据报道的滞后性和有些病例未被及时发现统计。总体来说，模型可以较好的描述疫情的发展规律，可以有效进行疫情跟踪预测、预警，为科学防控提供指导。

那么，面对突发传染病我们应当如何采取有效的防控措施呢？下面我们进行疫情传播基本再生数敏感性分析。

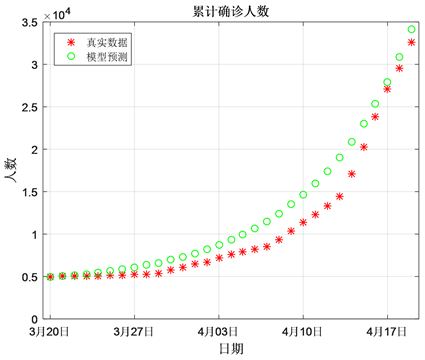
Figure 4. Fitting results of cumulative confirmed cases data

图4. 累计确诊人数数据拟合结果

4.4. 敏感性分析

定义1 函数 $\mu$ 关于变量x的标准化向前灵敏性指数为 [12] ： ${\xi }_x^u=\frac{x}{u}\times \frac{\partial u}{\partial x}$ 。

前面式(4)我们给出了基本再生数表达式：

$R_0=c\beta \left\{\frac{\sigma }{\omega }+\frac{\eta \left(1-p\right)}{{\gamma }_1+q_1}+\frac{p}{{\gamma }_2+q_2}\right\},$

带入模型获取的参数值，得到本次上海疫情基本再生数 $R_0=1.53$ 。

由表达式可得 $R_0$ 受参数 $c,\beta ,\sigma ,\eta ,\omega ,p,{\gamma }_1,{\gamma }_2,q_1,q_2$ 共10个参数的影响，其中参数 $p,\omega$ 反映了传染病自身的特点，属于不可控变量，所以我们只需分析 $R_0$ 关于 $c,\beta ,{\gamma }_1,{\gamma }_2,\sigma ,\eta ,q_1,q_2$ 的灵敏度变化。

分别求 $R_0$ 关于参数 $c,\beta ,{\gamma }_1,{\gamma }_2,q_1,q_2$ 的偏导数，计算如下：

$\frac{\partial R_0}{\partial c}=\beta \left[\frac{\sigma }{\omega }+\frac{\eta \left(1-p\right)}{{\gamma }_1+q_1}+\frac{p}{{\gamma }_2+q_2}\right]>0,\frac{\partial R_c}{\partial \beta }=c\left[\frac{\sigma }{\omega }+\frac{\eta \left(1-p\right)}{{\gamma }_1+q_1}+\frac{p}{{\gamma }_2+q_2}\right]>0,$

$\frac{\partial R_0}{\partial q_1}=\frac{\partial R_0}{\partial {\gamma }_1}=-c\beta \frac{\eta \left(1-p\right)}{{\left({\gamma }_1+q_1\right)}^2}<0,\frac{\partial R_c}{\partial q_2}=\frac{\partial R_c}{\partial {\gamma }_2}=-c\beta \frac{p}{{\left({\gamma }_2+q_1\right)}^2}<0,$

$\frac{\partial R_0}{\partial \sigma }=\frac{c\beta }{\omega }>0,\frac{\partial R_0}{\partial \eta }=\frac{c\beta \left(1-p\right)}{{\gamma }_1+q_1}>0,$

由导数的含义可知， $R_0$ 是关于 $\beta ,c,\sigma$ 和 $\eta$ 的增函数，随着 $\beta ,c,\sigma$ 和 $\eta$ 的增加而增加；是关于 ${\gamma }_1,{\gamma }_2,q_1,q_2$ 的减函数，随 ${\gamma }_1,{\gamma }_2,q_1,q_2$ 的增大而减少。

进一步，我们计算 $R_0$ 关于 $c,\beta ,{\gamma }_1,{\gamma }_2,\sigma ,\eta ,q_1,q_2$ 的灵敏性指数，得表达式如下：

${\xi }_{\beta }^{R_0}=\frac{\beta }{R_0}\times \frac{\partial R_0}{\partial \beta }=1,{\xi }_c^{R_0}=\frac{c}{R_0}\times \frac{\partial R_0}{\partial c}=1,$

${\xi }_{q_1}^{R_0}=\frac{q_1}{R_0}\times \frac{\partial R_0}{\partial q_1}=-c\beta q_1\frac{\eta \left(1-p\right)}{R_0{\left({\gamma }_1+q_1\right)}^2},{\xi }_{q_2}^{R_0}=\frac{q_2}{R_0}\times \frac{\partial R_0}{\partial q_2}=-\frac{c\beta q_{2}p}{R_0{\left({\gamma }_1+q_1\right)}^2},$

${\xi }_{\sigma }^{R_0}=\frac{\sigma }{R_0}\times \frac{\partial R_0}{\partial \sigma }=\frac{\sigma c\beta }{R_0\omega },{\xi }_{\eta }^{R_0}=\frac{\eta }{R_0}\times \frac{\partial R_0}{\partial \eta }=\frac{\eta c\beta \left(1-p\right)}{R_0\left({\gamma }_1+q_1\right)},$

${\xi }_{{\gamma }_1}^{R_c}=\frac{{\gamma }_1}{R_0}\times \frac{\partial R_0}{\partial {\gamma }_1}=-c\beta {\gamma }_1\frac{\eta \left(1-p\right)}{R_0{\left({\gamma }_1+q_1\right)}^2},$

${\xi }_{{\gamma }_2}^{R_c}=\frac{{\gamma }_2}{R_0}\times \frac{\partial R_0}{\partial {\gamma }_2}=-c\beta {\gamma }_2\frac{p}{R_0{\left({\gamma }_2+q_1\right)}^2},$

带入表1中的参数值，得到 $R_0$ 关于 $c,\beta ,{\gamma }_1,{\gamma }_2,\sigma ,\eta ,q_1,q_2$ 的灵敏性指数大小，结果见表2。

Table 2. Sensitivity index of parameters R 0

表2. $R_0$ 关于参数的灵敏性指数

由表2可以看出 $R_0$ 对参数 $\beta$ 和c最为敏感，接下来依次是 $\sigma ,\eta ,q_1,q_2$ 。且 $R_0$ 与 $\beta ,c,\sigma ,\eta$ 呈正相关，与 $q_1,q_2,{\gamma }_1,{\gamma }_2$ 呈负相关。这8个参数可以划分为三类：第一、反映疫情传播能力的参数： $\beta ,c,\sigma ,\eta$ ；第二、人为隔离确诊病例和无症状感染者的参数： $q_1$ 和 $q_2$ ；第三、反映确诊病例恢复速率的参数： ${\gamma }_1$ 和 ${\gamma }_2$ 。所以，理论上为了控制COVID-19的扩散，可以降低感染者的传染力 $\beta$ 和日接触率c；同时，增大确诊病例和无症状感染者隔离比例q，提高无症状感染者和显性感染者的恢复速率 ${\gamma }_1$ 和 ${\gamma }_2$ 。

5. 结论与建议

本文构建了一类带有无症状感染者和隔离仓室的SEIAQR传染病动力学模型，与一般模型相比该模型有明显的几点长处：1) 同时考虑了潜伏者、隐性感染者、显性感染者的存在性和传染性；2) 考虑了无症状感染者和显性感染者被发现隔离的情况；3) 用指数模型拟合模型系数；然后，基于第二代再生矩阵的方法给出了基本再生数 $R_0$ 的表达式，并进行了敏感性分析，数据拟合结果表明SEIAQR模型可以较好的跟踪预测疫情的发展规律。

结合参数的敏感性分析结果，我们为如何科学防控给出以下几点建议：1) 降低病毒传染力 $\beta$ ：公共场所按时进行通风消毒、公民出行严格佩戴口罩，并保持一米以上安全距离，不聚集。2) 降低日接触率c：加大核酸检测力度，加快病例确诊速率，并严格隔离感染者、密切接触者；同时，配合媒体宣传，提高人们的风险意识，减少不必要外出，避免接触。3) 增大隔离力度q：对于确诊感染者和无症状感染者、密切接触者、疑似病例等都要积极进行集中隔离治疗或观察；同时，公民要积极配合，若出现发烧、干咳等疑似症状，要立马就医检查，配合诊断，不要到处乱跑。4) 提高感染者的恢复速率 $\gamma$ ：积极接种新冠疫苗，增强抵抗病毒的能力。同时，积极完善医疗基础设施，研发治疗药物，给予病人充分的恢复治疗。

基金项目

河南省科技攻关项目(编号：222102320461)。

NOTES

^*通讯作者。