CNLS-p方程及其退化孤子解的研究

Study on CNLS-p Equation and Its Degenerate Soliton Solutions

摘要: 本文基于Darboux变换研究了CNLS-p方程，得到了一些位于零背景上的精确解，如孤子解、退化孤子解等。特别地，我们用数学软件绘制出了相应解的图像，并进行了动力学行为分析。此外，基于模平方的分解讨论了二阶退化孤子解的渐近形式，并展示了其近似轨道。

Abstract: In this paper, we study the CNLS-p equation based on the Darboux transformation, and obtain some exact solutions under the zero background condition, such as soliton solutions, degenerate soliton solutions, etc. Especially, we use mathematical software to draw the image of the corresponding solutions to analyze the dynamic behaviors. In addition, we discuss the asymptotic forms of the second-order degenerate soliton solutions by using the decomposition of the modulus square, and show their approximate orbits.

1. 引言

非线性薛定谔(NLS)方程是非线性科学和数学物理中的重要模型。它在光学、玻色–爱因斯坦凝聚、金融系统等方面有着广泛的应用 [1] [2] [3] 。近年来，由于许多重要的非线性物理现象无法用标准的NLS方程描述，含多组分高阶项的NLS方程越来越受到研究者的关注 [4] - [11] 。事实上，许多物理系统包含了具有不同模式、频率或偏振的相互作用波成分，这也使得耦合的NLS方程成为非线性系统的重要组成部分。

在本文中，我们主要研究以下耦合方程，也称为CNLS-p方程 [12] ：

$\begin{array}{l}\text{i}{u}_t^{\left(1\right)}+\frac{1}{2}{u}_{xx}^{\left(1\right)}+\sigma \left({\left|u^{\left(1\right)}\right|}^2+2{\left|u^{\left(2\right)}\right|}^2\right)u^{\left(1\right)}+\sigma \left(u^{\left(2\right)}{}^{{}^2}{u}^{\left(1\right)}{}^{*}\right)=0,\\ \text{i}{u}_t^{\left(2\right)}+\frac{1}{2}{u}_{xx}^{\left(2\right)}+\sigma \left({\left|u^{\left(2\right)}\right|}^2+2{\left|u^{\left(1\right)}\right|}^2\right)u^{\left(2\right)}+\sigma \left(u^{\left(1\right)}{}^{{}^2}{u}^{\left(2\right)}{}^{*}\right)=0,\end{array}$ (1)

其中 $u^{\left(1\right)}\left(x,t\right),u^{\left(2\right)}\left(x,t\right)$ 是复数， $\sigma =\pm 1$ ， ${}^{*}$ 表示复共轭。此系统已经被证明是潘勒卫可积的，并且具有双线性形式，也可以用来描述正交偏振光波在各向同性介质中的传播。

达布变换是构造可积系统的孤子解的一种非常有效的方法，它是一种规范变换，并不改变谱问题的形式。达布变换的基本思想是选取微分方程中易求得的解作为种子解，运动规范变换构造新解与种子解之间的迭代关系，进而求得方程的一系列精确解。

2. Lax对和达布变换

为了构造CNLS-p方程的达布变换，需要从方程的可积性和对称性入手。该方程具有如下形式的Lax对

$\begin{array}{l}{\Psi }_x=U\left(x,t;\lambda \right)\Psi =\text{i}\left(\lambda {\sigma }_3+Q\right)\Psi ，\\ {\Psi }_t=V\left(x,t;\lambda \right)\Psi =\left[\text{i}\left({\lambda }^2{\sigma }_3+\lambda Q\right)-\frac{1}{2}{\sigma }_3\left(\text{i}{Q}^2-Q_x\right)\right]\Psi ，\end{array}$ (2)

其中

${\sigma }_3=\left(\begin{array}{cccc}1& & & \\ & 1& & \\ & & -1& \\ & & & -1\end{array}\right),Q=\left(\begin{array}{cccc}0& 0& \sigma u^{\left(1\right)}{}^{*}& \sigma u^{\left(2\right)}{}^{*}\\ 0& 0& \sigma u^{\left(2\right)}{}^{*}& \sigma u^{\left(1\right)}{}^{*}\\ u^{\left(1\right)}& u^{\left(2\right)}& 0& 0\\ u^{\left(2\right)}& u^{\left(1\right)}& 0& 0\end{array}\right).$

相容性条件 $U_t-V_x+\left[U,V\right]=0$ 恰好可以产生方程(1)。

此外，矩阵 $U$ 和 $V$ 具有如下对称性：

$U^{†}\left(\lambda \right)=-JU\left({\lambda }^{*}\right)J,V^{†}\left(\lambda \right)=-JV\left({\lambda }^{*}\right)J$

基于上述分析，便可对CNLS-p方程构造达布变换：

$\begin{array}{l}{T}_1=I_4-\frac{\left({\lambda }_1-{\lambda }_1^{*}\right){\Psi }_0{\Psi }_0^{†}J}{\left(\lambda -{\lambda }_1^{*}\right){\Psi }_0^{†}J{\Psi }_0},\\ u^{\left(j\right)}\left[1\right]=u^{\left(j\right)}\left[0\right]-2\left({\lambda }_1-{\lambda }_1^{*}\right){\left(\frac{{\Psi }_0{\Psi }_0^{†}J}{{\Psi }_0^{†}J{\Psi }_0}\right)}_{1,j+2},\end{array}$ (3)

这里 ${\Psi }_0=\Psi \left(x,t,{\lambda }_1\right)={\left[\varphi ,\varphi ,\psi ,\psi \right]}^{\text{T}}$ 是线性方程(2)的一个特解。

接下来，我们构造达布变换的退化达布变换。将 ${\Phi }^{[m]}$ 在 ${\xi }_m$ 处进行泰勒级数展开，然后，借助一个极限过程，第一重退化达布变换为

$\begin{array}{l}{\Phi }_0^{[m]}\left[1\right]=\underset{\epsilon \to 0}{\lim }\frac{\left[{\tilde{T}\left[1\right]|}_{\lambda ={\xi }_m+\epsilon }\right]{\Phi }^{\left[m\right]}}{\epsilon }=\underset{\epsilon \to 0}{\lim }\frac{\left[\epsilon I_4+{\tilde{T}\left[1\right]|}_{\lambda ={\xi }_m}\right]{\Phi }^{\left[m\right]}}{\epsilon }={\Phi }_0^{\left[m\right]}+{\tilde{T}\left[1\right]|}_{\lambda ={\xi }_m}{\Phi }_1^{\left[m\right]},\\ u^{(j)}\left[1\right]=u^{\left(j\right)}\left[0\right]-2\left({\xi }_m-{\xi }_m^{*}\right){\left(P\left[1\right]\right)}_{1,j+2},\end{array}$ (4)

类似地，第二重退化达布变换可以通过以下方式实现：

$\begin{array}{l}{\Phi }_0^{\left[m\right]}\left[2\right]={\Phi }_0^{\left[m\right]}+\left(\left(\tilde{T}\left[2\right]+\tilde{T}\left[1\right]\right){\Phi }_1^{\left[m\right]}+\tilde{T}\left[2\right]\tilde{T}\left[1\right]{\Phi }_2^{\left[m\right]}\right){|}_{\lambda ={\xi }_m},\\ u^{\left(j\right)}\left[2\right]=u^{\left(j\right)}\left[1\right]-2\left({\xi }_m-{\xi }_m^{*}\right){\left(P\left[2\right]\right)}_{1,j+2},\end{array}$ (5)

其中

$\tilde{T}\left[1\right]=I_4-\frac{{\xi }_m-{\xi }_m^{*}}{\lambda -{\xi }_m^{*}}P\left[1\right],P\left[1\right]=\frac{{\Phi }_0^{[m]}{\Phi }_0^{[m]}{}^{{}^{†}}J}{{\Phi }_0^{[m]}{}^{{}^{†}}J{\Phi }_0^{[m]}}.$

进而，通过以上迭代步骤，可以继续推导出第三重退化达布变换甚至第N重退化达布变换。

3. CNLS-p方程的精确解

借助上述的退化达布变换我们来构造该方程的精确解。取零种子解，可以很容易地得到特征函数 $\Psi \left[0\right]$ 为

$\Psi \left[0\right]={\left[\varphi ,\varphi ,\psi ,\psi \right]}^{\text{T}},$ (6)

其中 $\varphi =\alpha {\text{e}}^{\text{i}\lambda \left(x+\lambda t\right)},\psi =\beta {\text{e}}^{-\text{i}\lambda \left(x+\lambda t\right)}$ ，应用上面介绍的达布变换，我们求得了方程(1)的一些解如下：

$u^{\left(j\right)}\left[1\right]=-2\left({\xi }_1-{\xi }_1^{*}\right){\left(\frac{{\Phi }_0^{\left[1\right]}{\Phi }_0^{\left[1\right]}{}^{{}^{†}}J}{{\Phi }_0^{\left[1\right]}{}^{†}J{\Phi }_0^{\left[1\right]}}\right)}_{1,j+2},$ (7a)

$u^{\left(j\right)}\left[2\right]=u^{\left(j\right)}\left[1\right]-2\left({\xi }_1-{\xi }_1^{*}\right){\left(\frac{{\Phi }_0^{\left[1\right]}\left[1\right]{\Phi }_0^{\left[1\right]}{\left[1\right]}^{†}J}{{\Phi }_0^{\left[1\right]}{\left[1\right]}^{†}J{\Phi }_0^{\left[1\right]}\left[1\right]}\right)}_{1,j+2},$ (7b)

$u^{\left(j\right)}\left[3\right]=u^{\left(j\right)}\left[2\right]-2\left({\xi }_1-{\xi }_1^{*}\right){\left(\frac{{\Phi }_0^{\left[1\right]}\left[2\right]{\Phi }_0^{\left[1\right]}{\left[2\right]}^{†}J}{{\Phi }_0^{\left[1\right]}{\left[2\right]}^{†}J{\Phi }_0^{\left[1\right]}\left[2\right]}\right)}_{1,j+2}$ (7c)

其中

$\begin{array}{l}{\Phi }_0^{\left[1\right]}\left[1\right]={\Phi }_0^{\left[1\right]}+{\Gamma }_1{\Phi }_1^{\left[1\right]},{\Phi }_0^{\left[1\right]}\left[2\right]={\Phi }_0^{\left[1\right]}+\left({\Gamma }_1+{\Gamma }_2\right){\Phi }_1^{\left[1\right]}+{\Gamma }_2{\Gamma }_1{\Phi }_2^{\left[1\right]},\\ {\Gamma }_1=I_4-\frac{{\Phi }_0^{\left[1\right]}{\Phi }_0^{\left[1\right]}{}^{†}J}{{\Phi }_0^{\left[1\right]}{}^{†}J{\Phi }_0^{\left[1\right]}},{\Gamma }_2=I_4-\frac{{\Phi }_0^{\left[1\right]}\left[1\right]{\Phi }_0^{\left[1\right]}{\left[1\right]}^{†}J}{{\Phi }_0^{\left[1\right]}{\left[1\right]}^{†}J{\Phi }_0^{\left[1\right]}\left[1\right]},j=1,2.\end{array}$

那么精确解的表达式为

$u^{\left(1\right)}\left[1\right]=\frac{4{\text{e}}^{2x+2it}}{4{\text{e}}^{4x}+1},u^{\left(2\right)}\left[1\right]=u^{\left(1\right)}\left[1\right],$ (8a)

(8b)

$u^{\left(1\right)}\left[3\right]=4096{\text{e}}^{2x+2it}\frac{A_1}{B_1},u^{\left(2\right)}\left[3\right]=u^{\left(1\right)}\left[3\right]$ (8c)

其中

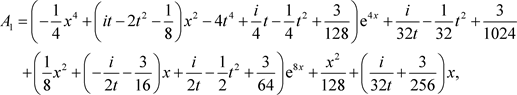
下面，我们讨论所求得的解的一些动力学性质，见图1。我们在图1中给出了二阶退化孤子解的三维图和密度图。二阶退化孤子解是是由Matveev在处理KdV方程时提出的，与量子物理场中的超透明势具有很强的相关性。它被看作是孤子的长程类似物，是缓慢退化的解。从图1，我们容易看出二阶退化孤子解是光滑的，并且在 $t=0$ 时刻，二阶退化孤子解的两个分支相互作用最强烈，在原点处形成类怪波，同时，振幅增大到最高约1.8。之后，两个分支在 $t\to \infty$ 处完全分离。

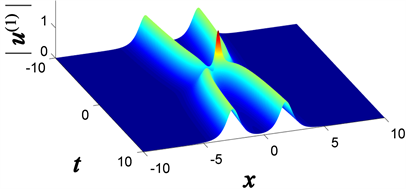
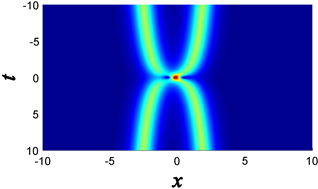
Figure 1. Three-dimensional and density diagrams of second-order degenerate solutions

图1. 二阶退化解的三维图和密度图

此外，我们发现，二阶退化孤子解的波形并不是一条恒定波形的行波，而是一条随时间平缓变化的曲线。为了近似刻画它们的轨迹，我们采用模平方分解的方法 [13] 。类比当 $\left|t\right|\to \infty$ 时，N-孤子解可以分解为N个具有“相移”的单孤子。我们对二阶退化孤子解进行如下分解：

性质当 $\left|t\right|\to \infty$ 时，PTCNLS方程的2-position解的模平方具有如下分解：

(9)

更精确的近似轨迹是由 $H\pm \frac{1}{4}\ln \left(1024t^2\right)=0$ 定义的两条曲线，见图2。图中显示了近似曲线与密度图的一致性，其中 $H=x$ 。

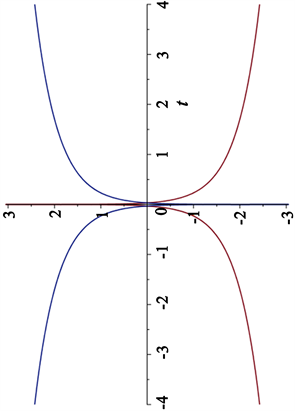
Figure 2. Asymptotic decomposition trajectory of the second-order degenerate soliton solution of CNLS-p equation

图2. CNLS-p方程的二阶退化孤子解的渐近分解轨迹图

4. 小结

本文基于达布变换方法，研究了零背景下CNLS-p方程的二阶退化孤子解，并对解的动力学行为进行了具体的分析。特别地，还对解进行了模平方分解，得出其分解之后的近似轨道图，且所得结果与实际解的图像有较好的吻合度。本工作使得CNLS-p方程的解更加丰富。此外，未来可以考虑进行分析在不同背景下该方程在达布变换作用下的精确解。