1. 引言
在高校教学中,为了更好地指导学生,我们需要根据学生的学习情况进行个性化的指导 [1] 。评价毕业生情况的一个重要指标是各门学科的成绩,这也是评价素质和效果的依据。十一名学员的考试成绩是衡量他们学习表现和教师教学质量的重要指标,可以通过学校的教务系统查询到他们的各项学习成绩,包括日常表现、次考试成绩以及综合素质评估结果。为了更准确地反映学生成绩的分布情况,我们使用K-means聚类计算对学员的多门学科成果加以分类 [2] 。通过对比不同类别学员的业绩,我们可以给出相应的指导建议,以便更好地评估学生的学习情况。此外,这种方法还可以为教学质量的反馈提供理论支撑 [3] 。
然而,K-means方法的最终聚合效果受到早期聚类中心的选择性的限制较大,而且很难准确地区分模糊类的属性。而对于模糊综合评价而言,我其中的隶属函数的赋予是个常见的痛点,而常用的指派法又太过于主观且无法充分利用已知样本数据 [4] 。对于上述二点,可以选择使用蒙特卡洛算法来大量尝试K-means初始聚类中心的选择,我并通过纪录其各个属性被划分到不同聚类的频率,来模拟一个隶属度,以此达到处理模糊聚类关系的目的 [5] 。
2. K-Means算法
K-means技术是一种有效的聚类分配技术,它的主要思路是:在给定K值和最初始簇核心的情况下,将各种数据内容分配到最近的簇核心所表示的类簇中,然后按照簇内的各种信息内容再次计算出该类簇的核心,并不断迭代,直至簇内核心的变异极小,甚至超过规定的迭代数量,从而实现有效的聚类分配(见图1)。
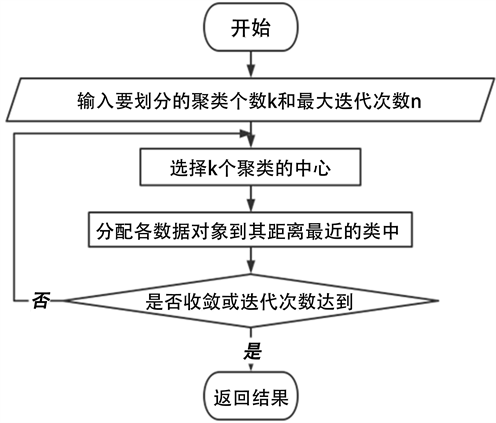
Figure 1. The flowchart of K-means algorithm
图1. K-means算法流程图
优点:
1) 该算法简单快速;
2) 对于处理大型数据集,该算法具有相对较高的性价比。
缺点:
1) 用户必须提前准备好生成的簇的数量k,以确保最佳性能;
2) 其最终的分类结果,会因初始聚类中心的选择不同,而发生较大的变化;
3) 对于孤立点的数据极为敏感。
4) 聚类结果,非此即彼,对于某些很难明确划分的属性来说,缺少可解释性。
K-means++算法在选择初始聚类中心时,应尽可能保持它们之间的距离较远,以便更好地捕捉和分析特征 [6] 。
步骤1:随机选择一个样本作为第一聚类中心;
步骤2:首先,测量每个采样点与当前现有聚类中心之间的最短时间。该值越大,采样点被选择为聚类中心的概率就越大;其次,使用轮盘赌方法(基于概率进行提取)从中选择最近的聚类中心;
步骤3:重复步骤2,直到选择了k个聚类中心。如果选择了两个或多个聚类中心,则取先前确定的聚类中心的重心。在选择了起点之后,仍然使用标准的K-均值算法。
3. 数据分析
数据源:学生成绩数据集.xlsx
(一) 算法配置:
算法:聚类分析(K-means)
变量:
{离散数学/4.0,高等数学A2/4.0,高级语言程序设计实训/1.0,线性代数/3.0,专业认识实习(计算机类)/0.5,思想道德与法治/2.0,体育/1.0,大学生职业生涯规划与就业指导/0.5,创业基础/0.5,大学物理A/4.0,大学英语2/3.0,“互联网+”与大学生创新创业/1.0,大学生心理健康教育/1.5,大学英语1/3.0,高等数学A1/5.0,高级语言程序设计/4.0,计算机导论/1.0,军事理论/0.5,中国近现代史纲要/2.0,应用文写作/2.0,形势与政策/1.0,体育/1.0.1,选修课/2.0,加权平均分}
参数:聚类个数:{4}。
(二)步骤
1) 先将数据集带入系统聚类,得到不同聚类数下的误差平方和。再将误差平方和绘制成折线图,根据肘部定理,确定聚类数。
2) 将数据带入到K-means聚类模型,通过蒙特卡罗随机选取初始点来进行聚类,并将每次聚类后该点所属类别记录下,最后求得各个样本在每个类中出现的频率。
3) 把每个样本对于每个类别的频率作为该样本对于每个聚类的隶属度。
4) 对分析进行综述。
(三)分析结论:
聚类分析基于数据特征,将所有样本划分为几类:2聚类结果共分为4类,聚类类别_1的频数为12,所占百分比为42.857%;聚类类别_2的频数为11,所占百分比为39.286%;聚类类别_3的频数为4,所占百分比为14.286%;聚类类别_4的频数为1,所占百分比为3.571%。
(四)详细结论分析:
1) 聚类数对比图(见图2)
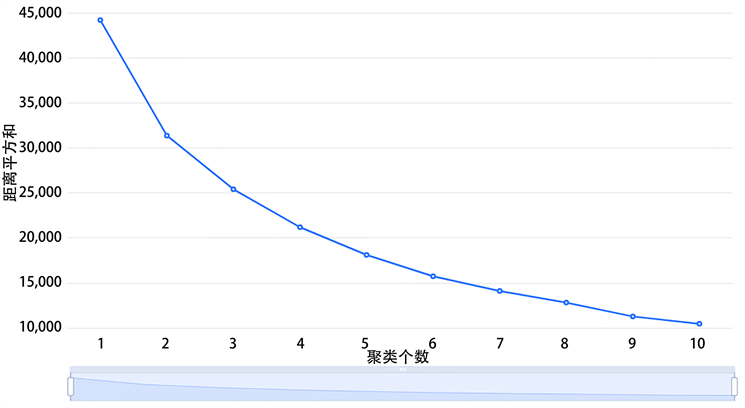
Figure 2. The result graph of elbow method
图2. 肘部法则结果图
这张图用于确定最佳的聚类数量,横坐标表示聚集的数量,纵坐标表示K平均聚集的损失函数,它反映了每个数据到类别中心的时间平方和,也意味着误差平方和(越小表明聚集效果越好)。可以通过“坡度趋于平缓”找出最佳的类簇数量。
这里选择了4为聚类数,以同时满足数据严谨性与可解释性。
2) 字段差异分析(详见表1)

Table 1. Field difference analysis display table
表1. 字段差异分析展示表
注:***、**、*分别代表1%、5%、10%的显著性水平。
上表展示了定量字段差异性分析的结果,包括均值 ± 标准差的结果、F检验结果、显著性P值。
● 分析每个分析项的P值是否显著(P < 0.05)。
● 如果它是显著的,并且原始假设被拒绝,则意味着两个数据集之间存在显著差异。可以使用平均值法±标准差来分析差异,反之亦然,这表明数据没有差异。
3) 聚类汇总(见表2)
上表展示了模型聚类的结果,包括频数、所占百分比。
4) 聚类汇总图(见图3)
上图以可视化的形式展示了模型聚类的结果,包括频数、所占百分比。
5) 聚类中心点坐标(见表3)

Table 3. Clustering centroid coordinates
表3. 聚类中心点坐标
6) 聚类散点图(见图4)
7) 评价指标
● 轮廓系数:这是一个重要的参数,用于测量样本集的样本,它可以反映出样本之间的相似性和差异性。轮廓系数的取值范围一般在[−1, 1]之间,越接近同一类别的样本,其轮廓系数就越大,从而提高聚类效果。
● DBI (Davies-boudin):这个指标用来衡量两个簇之间的距离,它是一个比值,表示簇内距离与簇间距离之比该指标越小表示聚类效果越好。
● 啊CH (Calinski-Harbasz Score):透过统计类内各点与类中央的间距平方和,可以衡量出类内的紧密集程度(分母),而透过统计类间的中心线与类别中心线的间距平方和,可以衡量出类别的分离度(分母)。CH指标是由分离度与紧密度的差值来决定的,CH越大,表明聚类效果越好。
8) 最终聚类模糊隶属度(见表4)

Table 4. Final clustering fuzzy affiliation
表4. 最终聚类模糊隶属度
4. 模型总结及评价
通过对于聚类后的四个类赋予基础解释性有:
类别1:各科成绩在班级中游,有部分学科偏弱,需要加强学习薄弱学科便能更上一层楼。
类别2:各学科成绩十分优秀,尤其是学分高的科目。这类学生稳定优秀,善于抓住主要矛盾
类别3:学业成绩不理想,分数相对落后。这类学生需要老师引导兴趣或给予帮助。
类别4:学习成绩比较偏科,部分学科成绩很差,但也有强势学科。老师应帮助引导,夯实弱项,发展强项。
上述这种由基础K-means引出的解释性分类难以考虑到极端情况,且单一的划分并不能做到很好的因材施教 [7] 。所以在此基础上我们通过引入模糊的隶属度概念,使一个学生可以同时隶属于多个类别,这样就产生的类别上更多的细分,同时在数据上教育者也更好的能分析该学生情况。
比如,某些学生因转专业或身体原因,部分课没有成绩,对于现有常用到K-means聚类,可能就误将其判为偏科。或者某个学生因竞赛或课程安排等原因,上学期的成绩与下学期的成绩很不一致,对于原有的K-means聚类也很难给出可信的解释。
或以上述第6号样本为例,在原K-means下被定义为第4类别,但实际上其对于第4类别的隶属度与对第2类别的隶属度几乎没有差异。且第4类别仅此一个样本,这就使得其原模型很难有好的解释性。
但增加了隶属度概念后,原本盖棺定论的“误判”会因隶属度的存在,稀释了特殊值或离群点对K-means的不利影响,进而有了可变性灵活性,使得聚类结果更具解释性。
5. 结语
K-means算法是一个极其经典的聚类算法,自提出以来,以其思想简单、聚类速度快、结果良好而得到广泛应用。K-means算法具有一些显著的优势,它能够有效地收敛域全局最优解,而且不会局限于一个局部最优解。但在这里,K-means的“非此即彼”的属性,容易产生小因子的偏差。在此基础上,我们引入蒙特卡罗及模糊隶属度,使得聚类的结果更具解释性,且有更多细分。这样就能更好地通过数学模型实现“因材施教”的目的。