基于GA-BP模型和李斯特操作线的铁直接还原度的预测研究

Study on Prediction of Iron Direct Reduction Degree Based on GA-BP Model and Rist Operation Line

摘要: 为实现“碳达峰、碳中和”目标和加快打造具有重要影响力的经济社会，着力推进工业绿色低碳转型和制造业高质量发展就必须从工业技术上改革。在高炉炼铁工艺过程中，铁的直接还原度在炼铁工艺中作为判断生产的重要指标系数，为决定生产强度起到关键作用。本文通过李斯特操作线模型计算铁的直接还原度，运用GA-BP算法建立了铁的直接还原度预测模型，并与支持向量机模型、随机森林模型进行预测结果对比。预测结果表明，GA-BP模型的MSE为0.012，MAE为0.08，R²达到0.92，预测性能明显优于另外两个预测模型，模型的拟合性更强。

Abstract: In order to achieve the goal of “carbon peak, carbon neutral” and accelerate the construction of a comprehensive green transformation zone with important influence on economic and social development, it is necessary to reform industrial technology to focus on promoting the green and low-carbon transformation of industry and high-quality development of manufacturing industry. In the process of blast furnace ironmaking, the direct reduction degree of iron plays a key role in determining the production intensity as an important production index coefficient in the ironmaking process. In this paper, the direct reduction degree of iron is calculated by the Rist operation line model, and the prediction results are compared with the support vector machine model and random forest model. The prediction results show that the MSE, MAE and R² of the GA-BP model are 0.012, 0.08 and 0.92, respectively. The prediction performance of the GA-BP model is obviously better than that of the other two prediction models, and the model has stronger fitting.

1. 引言

在双控制度和减污降排政策下，钢铁工业作为碳排放大户和污染物排放大户 [1] ，已经开始逐步向产品高质化、工艺绿色化、生产智能化方向发展 [2] 。高炉作为钢铁生产的原料基地，其焦化、烧结、球团等能耗与排污能力占比巨大 [3] ，高炉炼铁工序能耗占钢铁行业总能耗的73.6%，见图1。目前，随着计算机技术与钢铁工业的交叉融合，越来越多的机器学习模型和深度学习模型开始应用于高炉生产，如基于大数据技术的高炉焦比预测模型 [4] 、基于神经网络的高炉煤气利用率预测模型 [5] 、基于大数据的高炉煤气产销量预测研究 [6] 等，从根源上降低生产能耗、提升企业效益还需从工艺出发 [7] 。在高炉炼铁过程中，铁的直接还原度作为一项重要参考指标，其波动与碳消耗量、能量损耗、煤气利用率等有着重要影响关系，直接还原度增加就会造成反应耗能增大，碳消耗增多，提高生产成本 [8] 。目前，针对李斯特操作线的应用仅停留在铁直接还原度的计算，并没有将该值的深层冶金意义进行挖掘。因此，本文提出了一种基于遗传神经网络(Genetic Algorithm Back Propagation, GA-BP)的高炉铁直接还原度预测模型。首先以工艺理论为基础，通过李斯特操作线计算出还原度的值，然后与现场采集的数据合并后建立数据库，最后通过数据处理、特征工程等大数据分析技术，利用GA-BP神经网络建立基于铁的直接还原度的预测模型。

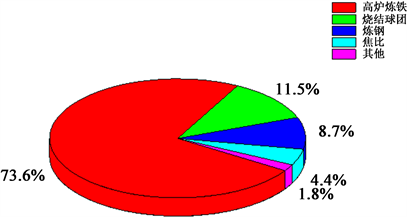
Figure 1. Proportion of blast furnace energy consumption

图1. 高炉能耗占比

2. 模型原理

2.1. Rist操作线的作用及应用

李斯特操作线是研究高炉冶炼参数与指标之间内在联系及规律的直角坐标系，也是高炉生产的重要分析工具。利用李斯特操作线对于了解高炉的运作状态分析具有重大意义 [9] 。由于李斯特操作线同时表达了高冶炼炉过程的两个基本现象：氧的交换和热平衡，并且表达形式比较简单、直观，所以李斯特操作线应用于当下许多方面：1) 分析风温、铁矿石预还原度、碳氢化合物喷吹量等操作变量对高炉利用系数、焦比、煤气利用率等的影响，以确定最佳操作条件；2) 校正测量数据，帮助发现检测仪器和称量设备的系统误差：3) 分析炉顶煤气气流分布对高炉燃料比的影响；4) 找出进一步提高煤气利用率和降低燃料比的新方法 [10] 。高炉实际生产会遇见外界因素的影响，从而影响顺行，人为操作因素的变化会影响李斯特操作线的两个方面：改变理想操作线的状态和改变实际操作的炉身工作效率，其原理就是实际操作线的斜率与理想操作线的斜率发生变化所造成的。

2.2. 铁的直接还原度

由于直接还原的计算和研究比较复杂，特别是现场生产情况下，很难直接判断直接还原的程度 [11] [12] ，理论上铁的直接还原度r_d，是根据铁氧化物的热力学分析，高炉内铁的高阶氧化物还原到氧化亚铁是以间接还原为主，而FeO到金属铁的还原，则是间接还原和直接还原共存。因此，铁的直接还原度定义为从氧化铁中以直接还原方式还原得到的铁量与全部被还原的铁量的比值 [13] [14] 。

$r_d=w_{直接还原铁}/w_{全铁}$ (1)

$\begin{array}{c}{R}_d=1-\frac{56}{m\left(\text{Fe}生\right)-m\left(\text{Fe}料\right)}\times [m\left(\text{C}气化\right)\times \frac{\rho \left({\text{CO}}_{\text{2}}\right)+\beta \rho \left({\text{H}}_{\text{2}}\right)}{12\left(\rho \left({\text{CO}}_{\text{2}}\right)+\rho \left(\text{CO}\right)+\rho \left({\text{CH}}_{\text{4}}\right)\right)}\\ -\frac{\left(1-{\gamma }_{{\text{CO}}_{\text{2}}}\right)m\left({\text{CO}}_2熔\right)+m\left({\text{CO}}_2矿焦\right)}{44}-\frac{m\left({\text{Fe}}_2{\text{O}}_3料\right)}{160}-\frac{m\left({\text{MnO}}_2料\right)}{87}]\end{array}$ (2)

2.3. Rist法计算铁的直接还原度

图2为李斯特操作线绘制图。在一定冶炼条件下，利用高炉状态绘制李斯特操作线，通过P、W点的A'E'直线，与原AE线比较，可以挖掘高炉节能降耗的潜力。因此，算出最低焦比时的理想操作线方程，就可以求出理论上的最佳还原度。理想操作线一定通过P点，联接并通过W、P两点的直线就可以得到。其与x = 0的纵坐标交于E'，与y_A平行于横坐标交于A'。

理想操作线的斜率：

$\mu =\frac{y_W-y_P}{x_W-x_P}$ (3)

又

$y_E=\mu \ast x_W-y_W$ (4)

得到理想操作线方程为：

$y_{A^{\prime }{E}^{\prime }}=\mu \ast x-y_{E^{\prime }}$ (5)

所以理论上最佳还原度为：

$rd=y_{d^{\prime }}=\mu \ast x-y_{E^{\prime }}$ (6)

直接还原度能反映高炉内直接还原反应发展的程度，也是炼铁工艺计算中常用的重要计算指标。铁的直接还原度从物料平衡的角度来计算复杂，容易出现计算错误，而李斯特操作线可以通过点与线的关系得到铁的直接还原度，将两者结合可以通过历史数据运输，计算并预测铁的还原度，进而为高炉生产提供参考 [15] 。

Figure 2. Rist operation line

图2. 李斯特操作线

3. 算法简介

3.1. BP神经网络

人工神经网络是学者受生物神经网络感知世界的原理启发而提出的一种数学模型，具有强大的处理非线性问题能力，是以往传统统计方法所不能完成的 [16] 。BP算法步骤：1) 网络初始化，拟定各连接权及阈值；2) 随机选取输入样本和对应期望值，由输入输出数据计算隐藏层、输出层的各单元输出；3) 重新定义新的连接权和阈值；4) 反复训练迭代直到网络误差符合预期，则结束算法。BP的运行特点就是权值更新、梯度计算、学习率 [17] 。首先，数据以向前传播。输出公式：

$y=f\left({\displaystyle {\sum }_{i=1}^n{w}_i{x}_i}-\theta \right)$ (7)

然后以均方误差公式反向传播，均方误差公式：

$E_k=\frac{1}{2}{\displaystyle {\sum }_{j=1}^l{\left({\stackrel{⌣}{y}}_j^k-y_j^k\right)}^2}$ (8)

通过方差求和可以将隐藏层的第j个节点的方差等于输出层与其连接的所有节点的方差与权值乘值的和，再乘以对该节点的导数。

$\frac{\partial E}{\partial w_{ij}}=\frac{\partial E}{\partial y_j}\times \frac{\partial y_j}{\partial w_{ij}}={\delta }_j^y\times x_i$ (9)

将输入层的方差传给隐藏层，然后一层一层反向传递往前影响层间权值和偏置。权值的更新公式

$\Delta w_{hj}=-\mu \frac{\partial E_k}{\partial w_{hj}}$ (10)

3.2. 构建GA-BP神经网络模型

遗传算法是模拟自然界生物进化机制的一种随机优化搜索算法 [18] 。BP神经网络虽然具有强大的数据预测能力，但对其影响最大的是初始权重和阈值的确定性，否则容易在训练搜索过程中出现局部最优，而不是全局最优的结果，而遗传算法就能达到优化初始权重和阈值。利用遗传算法对于BP神经网络的初始参数进行优化，得到最佳参数，从而使BP神经网络能更加科学、快速地完成模型的训练，增加模型的可靠性 [19] 。BP网络神经在进行模型运算处理时，数据会首先从输入端按层级权重到中间的隐含层，然后由隐含层作用的输出端，数据在输入端到隐含层和隐含层到输出端时会经过非线性处理，输出端通过误差反馈调节数据传递过程中的连接权重和阈值。BP神经网络的训练结果可以分为四个矩阵，矩阵输入节点为n，隐含层节点为i，输出层节点为r，则：

输入层到隐含层的权值矩阵为：

$X=\left[\begin{array}{ccc}{X}_{11}& \cdots & X_{1i}\\ ⋮& \ddots & ⋮\\ X_{n1}& \cdots & X_{ni}\end{array}\right]$

隐含层阈值矩阵为：

$W=\left[\begin{array}{c}{W}_1\\ W_2\\ ⋮\\ W_i\end{array}\right]$

隐含层到输出层权值矩阵为：

$Z=\left[\begin{array}{ccc}{Z}_{11}& \cdots & Z_{1r}\\ ⋮& \ddots & ⋮\\ Z_{i1}& \cdots & Z_{ir}\end{array}\right]$

输出层阈值矩阵为：

$Y=\left[\begin{array}{c}{Y}_1\\ Y_2\\ ⋮\\ Y_r\end{array}\right]$

GA遗传算法是根据自然界的遗传规律推演的一种计算机算法模型，以令A(t)表示第(t)代中串的群体，以 $A_j\left(t\right)\left(j=1,2,\cdots ,n\right)$ 表示第t代中第j个体串。设在第t代种群A(t)中该模式匹配成功的样本数量为m，记为 $m\left(H,t\right)$ 。令群体中整体的遗传数量为n，而群体中不同的个体之间所有的特性都存在着一定程度上的不一致。那么模式H在第t=1代中样本的数是：

$m\left(H,T+1\right)=m\left(H,t\right)n$ (11)

借助GA算法，能够对BP神经网络进行优化，整合优化过程可以通过上述矩阵进行，神经网络尤其是BP神经网络在对于解决复杂计算机网络安全评价问题方面有着举足轻重的作用 [20] 。

4. 数据处理及特征工程

通过收集承钢2021年生产数据，建立本地SQL (Structured Query Language) Server数据库对这些数据进行处理，包括原料成分、生铁成分、焦炭成分及各种物料数据等进行数据采集及清洗。

4.1. 数据预处理

在数据进行模型前需要对整体数据进行规范化处理，通常原始数据存在内部协变量偏移现象并且呈非线性，经过规范化处理后的数据指标可处于同一数量级，这也为了可以将数据进行更加综合性的评价，便于直观地观察数据之间的分布规律。不同的预测模型所需要的特征参数不同，衡量数据对目标的价值量需要借助冶炼机理、机器学习、统计分析等方法来做评判。如果用维度较多的特征参数数据进行模型预测，应该进行降维处理，即价值量很小的特征参数数据应该被合理地剔除，否则对预测效果极为不利 [21] 。

4.1.1. 时滞性

高炉自身的生产特点决定了高炉数据存在时间滞后性。时间滞后现象是当输入变量进入模型后，输出变量没有因为输入量立刻发生变化，而是过了一段时间才发生改变。在建立高炉预测模型时，如不考虑影响高炉各个生产参数的时滞性问题，那么建立的模型也将失去可行性和准确性。正确分析参数之间的相关性和滞后性是最关键的问题，一是高炉系统内发生反应造成的时滞性。另外，计算机进行数据传输需要一定时间造成的时滞性。通常计算机带来的时滞性与炉内反应的时滞性影响相对较小，故将目标参数延迟与其他参数保持时间一致即可。

4.1.2. 缺失值和异常值

高炉实际生产时，会发生不可预期因素(如设备故障、网络中断、服务器宕机等)导致监测数据缺失或异常，这些数值的出现和变化会影响高炉生产指标，且数据的缺失和处理异常值的方法也会对研究结果产生一定影响，所以采用可靠的解决方法具有重要的现实应用价值。国际上关于处理大数据上的缺失值和异常值一直都是研究者们非常关注的问题 [22] 。

关于缺失值的内在机理可以分为三种类型：完全随机缺失(Missing Completely At Random, MCAR)、非随机缺失(Missing Not At Random, MNAR)、随机缺失(Missing At Random, MAR)。完全随机缺失和非随机缺失指的是某个生产参数数据完全丢失空缺，但是这种情况较少发生。其中，随机缺失比非随机缺失更加常见也更符合现实，也是缺失值处理方法最主要的研究对象。随机缺失指的是在某个特定的组内缺失值是随机产生的，而不同组之间不一定是随机的，如果是因为设备故障导致数据缺失，数据往往会连续缺失一定时段直到设备运行正常，但大部分情况下缺失值是偶然出现的 [23] 。对采集的参数中空值和重复值进行删除。一般采用随机森林回归模型对参数变量中缺失数据进行缺失值填补，随机森林是一种基于决策树的集成算法，在建模过程中通过bootstrap随机抽样法构建样本集和训练模型。

在得到完整数据集后，一般通过绘制数据密度图来观察数据分布情况。首先采用算法对数据进行异常值分析，找到离群值，也就是和数据分布跨度大，有明显差异的数据，该数据对结果分析的有效性低，通常将其剔除。在数据整体存在较多异常情况下，需进行加深的异常值处理。对于异常值采用孤独森林模型进行处理，该算法模型可以捕捉到异常值并进行异常值的整改填回 [24] 。

图3为部分参数的箱线图结果，横坐标参数名称见表1。通过数据分析可以看到，对于不同参数的异常值分布，数据整体存在较多异常情况。利用孤独森林算法模型对异常值进行提取，由于孤独森林模型是基于树模型的集成模型，所以需要通过数据训练出n个子树：

1) 对于给定数据集X，采用随机抽样法抽取D个子集放入根节点：

$X=\left\{x_1,x_2,\cdots ,x_n\right\}\to X^{\prime }=\left(x_{i1},\cdots ,x_{id}\right)$ (12)

2) 从t个特征维度制定单个维度q，采用随机原则产生切割点P；

$\min \left(x_{ij},j=q,x_{ij}\in X^{\prime }\right)<p<\max \left(x_{ij},j=q,x_{ij}\in X^{\prime }\right)$ (13)

3) 对数据空间用过切割点p生成的超平面划分为两个子空间，对于维度小于p的放入左子节点，大于则放入右子节点；

4) 通过递归(1)和(2)将子树集达到预期高度；

5) 循环所有步骤，直到生成n个树集。

对于捕捉到的异常值，孤立森林算法所提供的接口可将异常值所对应的数据索引进行缓存，便于后续对异常值处理后对应填回数据 [25] 。

Figure 3. Data box line diagram

图3. 数据箱线图

Table 1. Parameters of box line diagram

表1. 箱线图参数

因此，需要对数据进行标准化处理，以达到统一生产参数之间的单位，也消除参数之间的影响，将数据进行标准化也有一定的抗干扰作用。数据标准化公式：

$x^{*}=\frac{x_i-\bar{x}}{\sigma }$ (14)

$x=\frac{1}{n}{\displaystyle {\sum }_i^n{x}_i}$ (15)

$\sigma =\sqrt{\frac{1}{n-1}{\displaystyle {\sum }_{i=1}^n{\left(x_i-\bar{x}\right)}^2}}$ (16)

由于数据集中的生产参数繁多，有些生产参数数据值密集复杂，有些仅为个位数甚至小数，因此对于这种数据之间量级相差过大的问题，在选择输入参数之前必须先对特征参数进行标准化处理，才能更加准确地对特征参数进行比较分析。

4.2. 特征选择

高炉内涉及一系列物理化学反应，为了解铁的还原反应原理，同时在网络模型的构建中更加充分地反映各因素之间内在联系，提高预测模型的精确性，需要利用统计方法主成分分析(Principal Component Analysis, PCA)，首先通过正交变换将可能存在相关性的变量转换为一组线性不相关的变量，然后将转换后的这组变量整理的统计方法，将原始数据进行标准化处理后，选取关联性较高参数，通过降维化处理找到综合评价更高的隐含层变量。

主成分分析通过将数据标准化之后，需要对数据进行相关系数矩阵分析：

$R=\left(\begin{array}{cc}{r}_{11}& \begin{array}{ccc}{r}_{12}& \cdots & r_{1p}\end{array}\\ \begin{array}{c}{r}_{21}\\ ⋮\\ r_{p1}\end{array}& \begin{array}{ccc}\begin{array}{c}{r}_{22}\\ ⋮\\ r_{p2}\end{array}& \begin{array}{c}\cdots \\ \ddots \\ \cdots \end{array}& \begin{array}{c}{r}_{2p}\\ ⋮\\ r_{pp}\end{array}\end{array}\end{array}\right)$ (17)

$r_{ij}\left(i,j=1,2,\cdots ,p\right)$ 为标准化后变量 ${x^{\prime }}_i$ 与 ${x^{\prime }}_j$ 的相关系数且 $r_{ij}=r_{ji}$ 。

$r_{ij}=\frac{{\displaystyle {\sum }_{k=1}^n\left(x_{ki}-{\overline{x^{\prime }}}_i\right)\left(x_{kj}-{\overline{x^{\prime }}}_j\right)}}{\sqrt{{\displaystyle {\sum }_{k=1}^n{\left(x_{ki}-{\overline{x^{\prime }}}_i\right)}^2}{\displaystyle {\sum }_{k=1}^n{\left(x_{kj}-{\overline{x^{\prime }}}_j\right)}^2}}}$ (18)

当设定产生一个新的初始群体，设定所需条件，然后计算每个个体的适应值和提取特征值，以概率选择遗传因子，然后交叉处理，选择一个个体的时候，复制到新的群体；选择两个个体的时候，交叉插入到新的群体；选择一个个体进行变异插入到新群体，从而这样得到满足需求的新群体。

表2为最终选取的18个有参考意义且关联性较强的参数作为特征参数。图4是列举四个关键参数对铁的直接还原度的特征性表现，能够看出关联性强、呈线状分布。

Table 2. Characteristic parameter name

表2. 特征参数名称

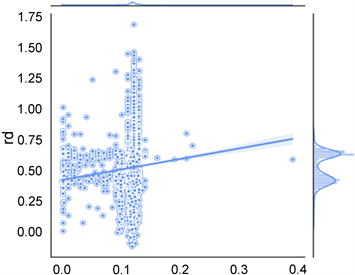
Figure 4. Correlation strength diagrams of some parameters

图4. 部分参数关联性强度图

5. 基于GA-BP铁的直接还原度预测分析

将所得的直接还原度真实值放入GA-BP神经网络模型中进行智能化训练迭代，所得出来的预测值与真实值趋向高度相似，可以作为参考模型对铁的直接还原度进行预测分析。中间层的神经元层数对整个网络模型有着至关重要的影响作用，但确定神经元层数的方法不唯一，通常采用算法(19)作为初步确定隐藏神经元数目的办法，然后根据实际情况进行调整修改。神经网络中传递函数、学习算法、学习效率、初始阈值和权重的选择也会对整个模型产生重大影响，初始阈值和权重由遗传算法优化得到，合适的算法是在模型训练过程中根据结果来确定最佳。

$N=\sqrt{m+n}+t$ (19)

式中：

N——中间层神经元数；

M——输入端神经元数；

N——输出端神经元数；

t——1~10之间的整数。

遗传算法最佳初始权重和阈值的过程中，确定合适的种群规模以及交叉变异概率，能让神经网络训练更快接近极限最优值，避免陷入局部最优解和算法不收敛情况。

由于预测模型多种多样，适应于不同数据类型，故采取三种不同的预测模型进行对比实验，选取精度高的预测模型进行预测分析：随机森林模型、GA-BP神经网络模型、支持向量机模型对铁的直接还原度进行预测分析。

Figure 5. Prediction image of random forest

图5. 随机森林预测图像

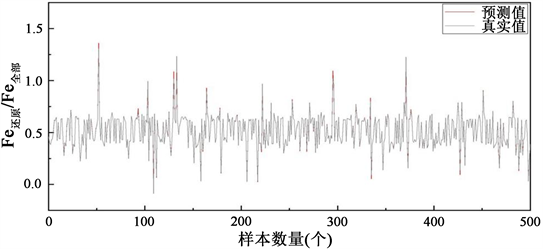
Figure 6. Prediction image of support vector machine

图6. 支持向量机预测图像

Figure 7. Prediction image of GA-BP neural network model

图7. GA-BP神经网络模型预测图像

为验证GA-BP神经网络在预测上的优良性，将输入特征参数合集分别用于随机森林算法预测模型(图5)和支持向量预测模型(图6)中进行比对分析，将预测结果和GA-BP神经网络预测模型(图7)进行对比。

精确判断预测模型的优良性，需采用均方差(Mean Square Error, MSE)、平均绝对误差(Mean Absolute Error，MAE)和决定系数(R²)来作为性能评价指标。

$\text{MSE}=\frac{1}{m}{\displaystyle {\sum }_{i=1}^m{\left(y_i-{\hat{y}}_i\right)}^2}$ (20)

$\text{MAE}=\frac{1}{m}{\displaystyle {\sum }_{i=1}^m\left|y_i-{\hat{y}}_i\right|}$ (21)

${\text{R}}^2=1-\frac{{\displaystyle {\sum }_i{\left({\hat{y}}_i-y_i\right)}^2}}{{\displaystyle {\sum }_i{\left({\bar{y}}_i-y_i\right)}^2}}$ (22)

式中：

M——样本数量；

y_i——真实值；

${\hat{y}}_i$ ——预测值；

${\bar{y}}_i$ ——平均值。

MSE表示样本整体真实值与预测值偏离程度，MSE越小，表示样本整体真实值与预测值偏离程度越小；MAE表示目标值和预测值之差的绝对值之和，MAE越小，表示样本征途真实值与预测值的损失值越少；R²系数表示用1减去残差平方和与总平方和的商，取值范围为[0, 1]，R²越大，表示模型预测精度高。三种预测模型的综合性能评判结果见表3。

Table 3. Comprehensive performance evaluation of three prediction models

表3. 三种预测模型的综合性能评判

由表3可知，GA-BP模型的R²较高，达到了0.926，均高于随机森林模型(Random Forest, RF)和支持向量机模型(Support Vector Regression, SVR)。由于对数据参数进行GA算法的处理，将阈值和权值都更新得到最优值，能降低预测算法的难度，所得预测值精度更高，故选用GA-BP神经网络模型作为预测模型进行真实值和测试值的对比，验证了GA-BP神经网络的预测准确度，见图8。

Figure 8. Comparison between prediction model and real value

图8. 预测模型与真实值对比

6. 结论

本文基于李斯特操作线理论研究了铁的直接还原度，建立遗传算法的BP神经网络模型。通过李斯特操作线作为理论基础，以数据神经网络作为延伸，对高炉中铁的直接还原度进行预测分析，得到如下结论：

1) 通过对高炉炼铁系统生产数据的缺失值、异常值进行规范化处理，有效地提高了预测模型的准确率。

2) 借助改进的特征选择法，开展了参数的特征选择和相关性分析研究，缩小了输入参数集合，提高了模型的精准度。

3) 建立了基于GA-BP神经网络算法的铁直接还原度的预测模型，并与随机森林模型、支持向量机模型进行了对比，显示了GA-BP模型预测性高于另外两个预测模型，其MSE为0.012，MAE为0.08，R²达到0.92，能够满足企业对铁直接还原度预测精度的要求。

4) 基于模型算法，以李斯特操作线作为理论基础，建立铁直接还原度的预测分析，为高炉操作人员提供了有效的数据支撑，能够辅助操作人员提前判断炉况。

基金项目

国家自然科学基金青年基金项目：52004096。

NOTES

^*通讯作者。