基于改进共同因子模型的死亡率预测模型

Mortality Prediction Model Based on Improved Common Factor Model

摘要: 人口死亡率的研究是与长寿风险相关的金融衍生品开发的理论依据，其研究的关键在于建立适合我国国情的死亡率模型，提高死亡率预测的准确性，考虑到中国人口死亡率数据较少且质量存在问题，仅使用我国死亡率数据建模不易得到好的预测结果。本文对共同因子模型进行改进创新，在其本身结构上加上经济项，并使用三个发展中国家和三个发达国家的历史死亡率数据进行拟合预测，结果表明，本文提出的新模型效果较好，弥补了仅依赖人口死亡率建模的缺点。

Abstract: The study of population mortality is the theoretical basis for the development of financial deriva-tives related to longevity risk, and the key to its research is to establish a mortality model suitable for China’s national conditions and improve the accuracy of mortality prediction. Considering the small amount and quality of China’s population mortality data, it is not easy to get good prediction results by modeling using only China’s mortality data. This paper improves and innovates the common factor model by adding an economic term to its own structure and fitting the prediction using historical mortality data from three developing countries and three developed countries, and the results show that the new model proposed in this paper works better and makes up for the shortcomings of relying only on population mortality modeling.

1. 引言

人口死亡率是寿险精算产品和基本养老金定价的基础，也是与长寿风险相关的金融衍生品开发的理论依据。利用随机动态死亡率模型进行死亡率预测是业界和学术界都十分关注的问题。目前，对多个人口的联合动态预测是研究热点，因为即使人们只对某一特定国家的预测感兴趣，多人口模型也有合并更多数据的优势。正如Li和Lee所指出的，通过考虑更大群体中的共同模式，可以改善单个人口的死亡率预测 [1] 。

目前常用的多人口随机死亡率模型主要包括Joint-k模型、ACF模型及其改进模型和CAE模型，这些模型通常将死亡率数据分解为时间因素、年龄因素来描述死亡率变化趋势，进而依靠预测时间因素来预测死亡率，是一种仅根据历史趋势外推预测死亡率的方法 [2] 。但我国对死亡率数据的统计工作开展地较晚且由于人口基数过大，数据质量较差，直接应用经典随机死亡率模型并不能取得较好的效果。

与此同时，为了弥补仅依赖人口死亡率建模预测的缺点，一些外生因素(如生物医学、环境或社会经济因素)对死亡率影响的研究也层出不穷，其中，研究最多的趋势之一是经济增长。例如，2005年，Brenner指出，至少十年来的经济增长是美国二十世纪死亡率下降的主要因素 [3] 。2011年，Hanewald使用1950年至2006年期间六个经合组织国家的数据，在Lee Carter死亡率预测模型中研究了宏观经济波动对死亡率的动态影响 [4] ，发现该模型中的死亡率指数与所考虑时期内国家的GDP水平之间存在显著相关性。2014年，Niu和Melenberg建立了死亡率指数k_t和宏观经济指标的向量误差校正模型(VECM) [5] ，并对Lee-Cater模型中的时间因素和人均GDP进行了Johansen协整检验，结果表明两者存在长期稳定的均衡关系，这种协整关系比Hanewald提出的结果强得多。Boonen和Li在2017年对上述做法进行扩展 [6] ，将以人均实际国内生产总值(GDP)为代表的经济增长包括在内，扩展了Li和Lee在2005提出的模型 [1] 以捕捉具有相似社会经济条件的人群的共同死亡率趋势，发现提出的模型提供了更好的样本内拟合和样本外预测性能。2022年，王梦珂和唐爽对Boonen和Li的模型加以改进 [7] ，把作为全局参数的人均GDP变量 $G\left(t\right)$ 变为局部参数 $g\left(t,i\right)$ ，打破了只能选择经济发展趋势相近的国家作为一组进行建模的局面，研究了包括中国在内的5个国家，结果表明改进后的新模型适合中国人口死亡率的预测，弥补了仅依赖人口死亡率建模预测的缺点。

本文受前人研究启发，创新地在共同因子模型ACF1，ACF3的本身结构上加上经济项，这里采用的是标准化后的人均GDP值，并将新模型命名为ACF1-GDP和ACF3-GDP，使用ACF1-GDP、ACF1、ACF3-GDP、ACF3这四个模型分别对三个发展中国家(中国、保加利亚、智利)和三个发达国家(美国、日本、英国) 1995~2017年的历史死亡率数据进行参数拟合，并对中国、智利、美国、日本、英国2018~2020年，保加利亚2018~2021年的死亡率进行预测，最后将ACF1-GDP、ACF1、ACF3-GDP、ACF3预测结果误差用绝对拟合误差AFE来度量，以此探究加上经济项后的效果是否良好，结果表明提出的新模型ACF1-GDP和ACF3-GDP的预测误差对所研究的大部分国家在大多数时候要比ACF1、ACF3的预测误差小，证明本文对共同因子模型的改进效果良好。

2. 模型介绍

2.1. 模型提出

Li等 [1] 考虑多人口之间的共同趋势，提出了增强共同因子模型，即ACF模型：

$\log m\left(x,t,i\right)=a\left(x,i\right)+B\left(x\right)K\left(t\right)+b\left(x,i\right)k\left(t,i\right).$ (1)

Enchev等 [8] 将ACF模型中的 $b\left(x,i\right)$ 换为 $B^{\left(2\right)}\left(x\right)$ ，提出了ACF1模型：

$\log m\left(x,t,i\right)=a\left(x,i\right)+B^{\left(1\right)}\left(x\right)K\left(t\right)+B^{\left(2\right)}\left(x\right)k\left(t,i\right).$ (2)

马海飞 [9] 对ACF模型变形，将其中的 $k\left(t,i\right)$ 换为 $K^{\left(2\right)}\left(t\right)$ , 提出了ACF3模型：

$\log m\left(x,t,i\right)=a\left(x,i\right)+B\left(x\right)K^{\left(1\right)}\left(t\right)+b\left(x,i\right)K^{\left(2\right)}\left(t\right).$ (3)

对于ACF1模型， $m\left(x,t,i\right)$ 表示第i个人群中x岁的人在年份t的中心死亡率， $a\left(x,i\right)$ 描述特定年龄人口的平均死亡率水平，且有：

$a\left(x,i\right)=\frac{{\displaystyle {\sum }_t\log m\left(x,t,i\right)}}{T}.$ (4)

Figure 1. Average mortality levels by country ( $a\left(x,i\right)$ )

图1. 各国平均死亡率水平( $a\left(x,i\right)$ )

从图1看出，各个国家的对数死亡率的平均水平随着年龄的增长，其值均呈现了先下降后上升的趋势，体现了不同国家对数死亡率的平均水平随着年龄的增长变化的一种共性。

$K\left(t\right)$ 为共同时间因子，反映全年龄总体人口对数死亡率随时间变化的共同趋势； $k\left(t,i\right)$ 为附加时间因子，反映第i个人群对数死亡率随时间变化的趋势； $B^{\left(1\right)}\left(x\right)$ ， $B^{\left(2\right)}\left(x\right)$ 为共同年龄因子，分别表示特定年龄总体人口对 $K\left(t\right)$ 和 $k\left(t,i\right)$ 变化的敏感度。

对于ACF3模型， $K^{\left(1\right)}\left(t\right),K^{\left(2\right)}\left(t\right)$ 为共同时间因子， $B\left(x\right)$ 为共同年龄因子， $b\left(x,i\right)$ 是附加年龄因子，代表第i个人群对共同时间因子 $K^{\left(2\right)}\left(t\right)$ 的敏感度。

本文分别在ACF1和ACF3模型后加上 $\gamma \left(x,i\right)$ 和 $g\left(t,i\right)$ 的乘积项， $g\left(t,i\right)$ 表示第i个人群在t年的标准化后的人均GDP值，将 $g\left(t,i\right)$ 标准化后用于建模，这意味着本文考虑的是经济变化趋势对人口死亡率变动的影响， $\gamma \left(x,i\right)$ 反映特定年龄人口死亡率对经济因素变化的敏感程度。并将新模型分别命名为ACF1-GDP和ACF3-GDP，模型形式如下：

ACF1-GDP：

$\log m\left(x,t,i\right)=a\left(x,i\right)+B^{\left(1\right)}\left(x\right)K\left(t\right)+B^{\left(2\right)}\left(x\right)k\left(t,i\right)+\gamma \left(x,i\right)g\left(t,i\right).$ (5)

ACF3-GDP：

$\log m\left(x,t,i\right)=a\left(x,i\right)+B\left(x\right)K^{\left(1\right)}\left(t\right)+b\left(x,i\right)K^{\left(2\right)}\left(t\right)+\gamma \left(x,i\right)g\left(t,i\right).$ (6)

Figure 2. Average mortality levels by country ( $a\left(x,i\right)$ )

图2. 标准化后人均GDP( $g\left(t,i\right)$ )

从图2看出，只有中国标准化后的人均GDP没有明显的下降趋势，其他国家图线走向均有明显变化，这意味着六国中只有中国的经济水平始终在平稳增长。

2.2. 参数估计

对于ACF1-GDP， $B^{\left(1\right)}\left(x\right)$ ， $B^{\left(2\right)}\left(x\right)$ ， $K\left(t\right)$ 为全局参数， $k\left(t,i\right)$ ， $\gamma \left(x,i\right)$ ， $g\left(t,i\right)$ 为局部参数，且 $g\left(t,i\right)$ 为已知量。

该模型的参数估计大致通过以下两步完成：

第一步：将所有人口死亡率用于计算全局参数；

第二步：在全局参数已知的条件下，用最小二乘法拟合未知的局部参数。

$U\left(x,t\right)=\frac{{\displaystyle {\sum }_i\left(\log m\left(x,t,i\right)-a\left(x,i\right)\right)}}{I},$ (7)

其中，I表示样本内人口类别总数， $U\left(x,t\right)$ 包含所有人口死亡率信息，被用于第一步全局参数的计算。通过对 $U\left(x,t\right)$ 进行奇异值分解得到全局参数 $B^{\left(1\right)}\left(x\right)$ ， $B^{\left(2\right)}\left(x\right)$ ， $K\left(t\right)$ 。然后令

$U_i\left(x,t\right)=B^{\left(1\right)}\left(x\right)K\left(t\right)+B^{\left(2\right)}\left(x\right)k\left(t,i\right)+\gamma \left(x,i\right)g\left(t,i\right).$ (8)

根据最小二乘法 [10] 得到以下参数迭代公式：

$k\left(t,i\right)=\frac{{\displaystyle {\sum }_{x=1}^n{B}^{\left(2\right)}\left(x\right)}\left(U_i\left(x,t\right)-B^{\left(1\right)}\left(x\right)K\left(t\right)-\gamma \left(x,i\right)g\left(t,i\right)\right)}{{\displaystyle {\sum }_{x=1}^n{B}^{\left(2\right)}{\left(x\right)}^2}},$ (9)

$r\left(x,i\right)=\frac{{\displaystyle {\sum }_{t=1}^{T}g\left(t,i\right)}\left(U_i\left(x,t\right)-B^{\left(1\right)}\left(x\right)K\left(t\right)-B^{\left(2\right)}\left(x\right)k\left(t,i\right)\right)}{{\displaystyle {\sum }_{t=1}^{T}g{\left(t,i\right)}^2}},$ (10)

基于Niu和Melenberg [5] 、Boonen和Li [6] 的做法，为了确保参数估计结果的唯一性，添加以下约束：

${\displaystyle \underset{t}{\sum }k\left(t,i\right)}=0.$ (11)

对于ACF3-GDP， $K^{\left(1\right)}\left(t\right)$ ， $K^{\left(2\right)}\left(t\right)$ ， $B\left(x\right)$ 为全局参数， $b\left(x,i\right)$ ， $\gamma \left(x,i\right)$ ， $g\left(t,i\right)$ 为局部参数，与ACF1-GDP拟合步骤类似，局部参数迭代公式和约束如下：

$b\left(x,i\right)=\frac{{\displaystyle {\sum }_{t=1}^T{K}^{\left(2\right)}\left(t\right)\left(U_i\left(x,t\right)-B\left(x\right)K^{\left(1\right)}\left(t\right)-\gamma \left(x,i\right)g\left(t,i\right)\right)}}{{\displaystyle {\sum }_{t=1}^T{K}^{\left(2\right)}{\left(t\right)}^2}},$ (12)

$r\left(x,i\right)=\frac{{\displaystyle {\sum }_{t=1}^{T}g\left(t,i\right)\left(U_i\left(x,t\right)-B\left(x\right)K^{\left(1\right)}\left(t\right)-b\left(x,i\right)K^{\left(2\right)}\left(t\right)\right)}}{{\displaystyle {\sum }_{t=1}^{T}g{\left(t,i\right)}^2}},$ (13)

${\displaystyle \underset{x}{\sum }b\left(x,i\right)}=1.$ (14)

3. 预测结果分析

3.1. 数据来源

本文搜寻人类死亡数据库，选取了中国、智利、保加利亚这3个发展中国家和美国、日本、英国这3个发达国家的死亡率为研究对象。其中，智利是南美洲最发达的国家，保加利亚位于欧洲，2021年保加利亚人均GDP为1.22万美元，与中国的1.26万美元相近。

本文采用的中国死亡率数据来源于1995~2020年的《中国人口统计年鉴》，其他国家的数据均来自人类死亡率数据库，由于保加利亚数据更新较快，其研究数据区间为1995~2021年，其余国家死亡率数据均只更新到了2020年。由于死亡率数据在高年龄段的瞒报、错报现象较为严重，故本文只采用了各国各年0~89岁的死亡率数据。

3.2. 参数估计结果

根据2.2给出的迭代公式，应用R软件对六国1995~2017年的0~89岁的历史死亡率数据进行参数拟合，得到了各全局参数和局部参数的拟合值，并做出图3、图4和图5使其可视化。

$B^{\left(1\right)}\left(x\right)$ $K(\; t\; )$

$B^{\left(2\right)}\left(x\right)$ $K^{\left(2\right)}(\; t\; )$

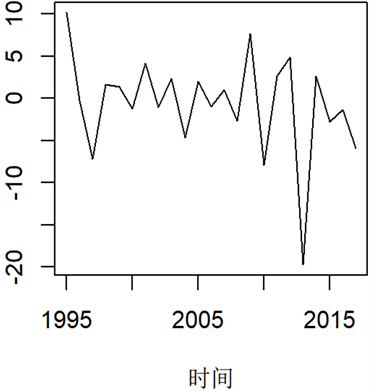
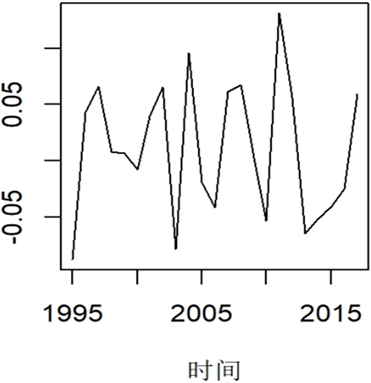
Figure 3. Results of global parameter estimation for ACF1-GDP and ACF3-GDP

图3. ACF1-GDP和ACF3-GDP全局参数估计结果

在图3中，由于全局参数均由 $U\left(x,t\right)$ 通过奇异值分解得出，所以 $B^{\left(1\right)}\left(x\right)$ ， $K\left(t\right)$ 也分别为ACF3-GDP中的 $B\left(x\right)$ ， $K^{\left(1\right)}\left(t\right)$ 。

$K\left(t\right)$ 变化波动较大，总体呈较明显的下降趋势，全局时间参数 $K\left(t\right)$ 相较于 $K^{\left(2\right)}\left(t\right)$ 更能代表全局的共同时间因子，反映六个国家人口死亡率整体改善状况。

$k\left(t,i\right)$ $\gamma \left(x,i\right)$

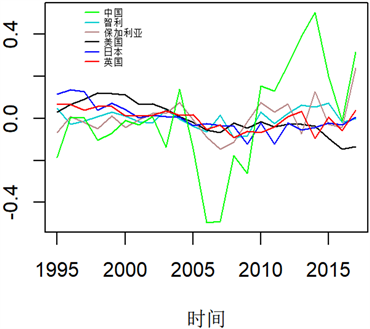
Figure 4. ACF1-GDP local parameter estimation results

图4. ACF1-GDP局部参数估计结果

虽然图3显示 $B^{\left(2\right)}\left(x\right)$ 波动幅度较大，但图4中局部年龄 $k\left(t,i\right)$ 的值在0值附近上下波动，所以 $B^{\left(2\right)}\left(x\right)$ 对死亡率的影响较小， $B^{\left(1\right)}\left(x\right)$ 虽然为正值，但 $K\left(t\right)$ 在大多数年份为负值，且绝对值较大，所以使得死亡率下降，0~20岁的 $B^{\left(1\right)}\left(x\right)$ 绝对值要高于其他年龄段，表示这一年龄段人口死亡率改善状况要优于其他年龄段，死亡率下降速度更快。同样，0~20岁左右以及80岁以上的 $B^{\left(2\right)}\left(x\right)$ 绝对值较大，表示这两个年龄段人口死亡率改善状况相对优于其他年龄段。

$b\left(x,i\right)$ $\gamma \left(x,i\right)$

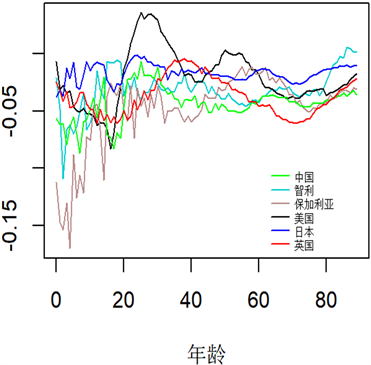
Figure 5. ACF3-GDP local parameter estimation results

图5. ACF3-GDP局部参数估计结果

观察对比图4 ACF1-GDP模型和图5 ACF3-GDP模型中的 $\gamma \left(x,i\right)$ 值，发现只有中国的 $\gamma \left(x,i\right)$ 值在两个模型间具有明显差异，其原因主要在于中国的 $k\left(t,i\right)$ 值和 $b\left(x,i\right)$ 值相较于其他国家来说波动较大。图4和图5都显示美国的 $\gamma \left(x,i\right)$ 值在30岁左右的部分年龄段大于0，这意味着随着经济增长，该年龄段死亡率上升，这代表美国并不适合提出的新模型。

图4和图5中，智利、保加利亚、日本、英国的 $\gamma \left(x,i\right)$ 值均为负值，对于这些国家来说，经济增长对各年龄段人口死亡率的降低有积极作用，也更适合本文提出的新模型。且中国、智利、保加利亚0-5岁左右的 $\gamma \left(x,i\right)$ 绝对值较高，这说明对于发展中国家，该年龄段人口死亡率下降仍明显受益于经济增长，并且主要受益于随着经济增长带来的医疗水平的提高。而美国的 $\gamma \left(x,i\right)$ 值在大部分年龄段围绕0值小幅波动，反映美国人口死亡率下降对经济增长趋势并不敏感，这也部分解释了近年来一些发达国家人口死亡率下降趋势并不明显的事实。

3.3. 预测效果的比较

根据1995~2017年的历史数据对模型的参数进行拟合，然后用带漂移项的随机游走对这23年的时间项参数 $K\left(t\right)$ ， $k\left(t,i\right)$ (ACF1、ACF1-GDP中)和 $K^{\left(1\right)}\left(t\right)$ ， $K^{\left(2\right)}\left(t\right)$ (ACF3、ACF3-GDP中)进行预测，这

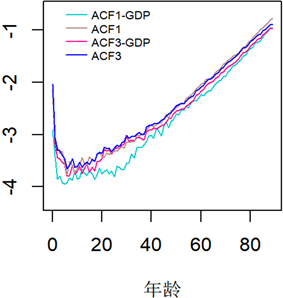
2018年预测值对比 2019年预测值对比2020年预测值对比 2021年预测值对比

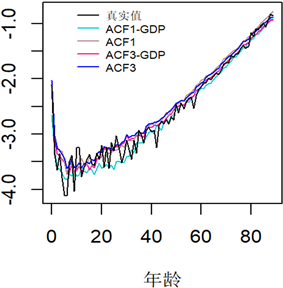
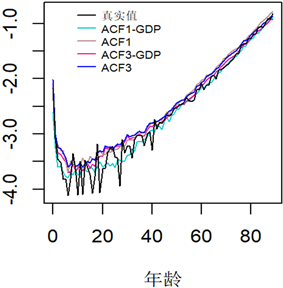
Figure 6. Comparison of logarithmic mortality projections for China, 2018 to 2020

图6. 2018~2020年中国对数死亡率预测值对比

里向后预测了4年的时间项，即从2018年到2021年，然后将预测的时间项参数以及拟合得到的各年龄项参数和 $\gamma \left(x,i\right)$ 分别代入模型ACF1-GDP，ACF1，ACF3-GDP，ACF3中，得到这4年的死亡率预测值。

根据得到的中国死亡率预测值，做出了2018~2021年的对数死亡率预测值对比图(图6)，可以看出本文提出的新模型ACF1-GDP对比ACF1，ACF3-GDP对比ACF3预测效果较好，2021年中国实际的死亡率数据没有更新，所以只作出了2021年四个模型的预测对比。

接下来采用AFE (绝对拟合误差)来评估ACF1-GDP，ACF1，ACF3-GDP，ACF3这四个模型对所研究的6个国家的预测效果。AFE表达式为：

${\text{AFE}}_{t,i}=\underset{x}{{\displaystyle \sum }}\left|m_{x,t,i}-{\hat{m}}_{x,t,i}\right|.$ (15)

其中，保加利亚的死亡率数据更新到2021年，其他5个国家都是更新到了2020年。根据这4个模型对每个国家每年的死亡率预测的AFE值，我们做出了下面的图：

Figure 7. Comparison of errors in mortality projections for six countries

图7. 六国死亡率预测误差对比

从图7中看出，在这六个国家中，中国和日本最适合本文提出的加入经济因素的新模型，因为对于这两个国家，ACF1-GDP和ACF3-GDP的AFE值一直都分别比ACF1，ACF3的小，这说明加入经济项的新模型提高了共同因子模型的预测性能。对于保加利亚、智利和英国，在2018年、2019年ACF1-GDP和ACF3-GDP模型效果更好，2020、2021年时，ACF1和ACF3的 值更小，模型效果更好，分析其原因认为在2020和2021年，新型冠状病毒肺炎肆虐，对欧洲国家的影响较大，与经济因素相比，该呼吸道传染病已成为对死亡率影响更大的因素。而对于美国，从20世纪起就一直位于发达国家前列，经济增长不够明显，故一直都是不加经济因素的ACF1，ACF3模型效果更好，所以对于类似美国的超发达国家，本文提出新模型的适用性仍然有待研究。

4. 结论

本文在前人研究基础上，提出了新模型ACF1-GDP和ACF3-GDP，使用三个发展中国家(中国、保加利亚、智利)和三个发达国家(美国、日本、英国)的部分历史死亡率数据，将ACF1-GDP模型与ACF1模型的预测结果对比，ACF3-GDP模型与ACF3模型预测结果对比，以此探究加入经济项后的效果是否良好，结果表明，在这六个国家中，中国和日本最适合本文提出的加入经济因素的新模型。

对于保加利亚、智利和英国，在2018年和2019年，ACF1-GDP与ACF3-GDP模型效果更好，在2020和2021年，ACF1与ACF3的模型效果更好，分析其原因认为在2020和2021年，新型冠状病毒肺炎肆虐，对欧洲国家的影响较大 [11] ，与经济因素相比，该呼吸道传染病已成为对死亡率影响更大的因素。故后续研究可以从加入新型冠状病毒肺炎的影响因素项来入手，为多人口死亡率研究做出新的尝试。在疫情逐渐趋于平稳化的今天，本文提出的ACF1-GDP与ACF3-GDP模型对于大部分发达国家与发展中国家的死亡率预测将会有更大的优势。

基金项目

本文由国家自然科学基金项目(12061066)支持。