Mathematica在电磁学教学中的应用

Application of Mathematica in Electromagnetism Teaching

摘要: Mathematica是目前世界上广泛使用的计算模拟软件，具有功能全面、入门难度低、可进行符号和数值混合计算等优点。而在《大学物理》电磁学部分的教学中，为了提高学生学习效率，加深理解，我们讨论利用Mathematica软件进行模拟训练，以提高学生的动手实践能力和学习的主动性，提高教学效果。

Abstract: Mathematica is a widely used computational simulation software in the world, with advantages such as comprehensive functionality, low entry difficulty, and the ability to perform symbol and numerical mixed calculations. In the teaching of electromagnetism in College Physics, in order to improve students’ learning efficiency and deepen their understanding, we discussed the use of Mathematica software for simulation training, so as to improve students’ practical ability and learning initiative, and improve the teaching effect.

1. 引言

物理学的教学方向主要包括：物理理论知识、物理实验和物理计算。其中，物理计算模拟是指把复杂的物理问题进行数学建模，再根据计算的复杂程度和目标精度设计合适的算法，并将数学语言转化为程序语言，进而得到严谨结论的综合过程 [1] 。在通常的《大学物理》课程中都缺乏相关内容的教学，这会降低部分学生的知识转化效率，常见的现象有：学生在参与物理类学术竞赛和大创项目时没有思路，或者物理课程与理工科专业课程之间存在过渡困难的情况。其次，如今已处在智能时代，学生面对的潜在物理问题，已与课后习题产生明显的差距，解决二者的思路和方法可能有所不同。这就要求学生掌握更现代化的手段和技能。在这个趋势下，大学物理也需要随之变化。因此，我们认为有必要在现有的大学物理教学框架中增加关于物理计算模拟的相关内容。

电磁学在《大学物理》课程中，属于一个比较抽象的部分，原因有二：首先，电磁场看不见摸不着，不是实物粒子，很难通过直接展示让学生们理解其性质；其次，该部分涉及到了多重积分和梯度等概念，对于刚刚学习高等数学的学生而言有一定的难度，需要辅助工具帮其进行大量的实践以加深理解 [2] 。因此选用合适的模拟软件可以起到事半功倍的效果。目前在电磁学教学中使用的主流计算软件有：ANSYS [3] 、MATLAB [4] [5] [6] [7] 、Python [8] 和Mathematica [9] 等。其中，Mathematica是由Wolfram Research公司在1988年发布的科学计算软件，到目前位置已经历经13个版本。与其他软件相比，Mathematica具有可同时进行符号计算和数值计算的特点，其编程语言接近自然语言，内置比较完善的数学算法，对于学生而言入手难度低，可以让学生更高地将重点放在物理公式和数学计算原理中，而不必为数值算法等问题分心。我们这篇文章着重介绍Mathematica软件在《大学物理》教学中电磁学部分的应用和实践。

2. Mathematica在电场中的应用

Figure 1. 3D vector diagram of electrostatic field generated by point charges in vacuum

图1. 真空中点电荷产生的静电场三维矢量图

在《大学物理》的静电场课程主要讨论真空中点电荷(系)所产生的静电场，其表达式为

$E=\frac{q}{4\pi {\epsilon }_0{r}^3}r$ (1)

与中学阶段的学生经常处理的匀强电场不同，《大学物理》中更加强调物理量的矢量性，因此需要为学生展示空间中不同位置处电场的大小和方向均不同。而Mathematica具有非常强的矢量运算和画图能力。在Mathematica语言环境中{x, y, z}这样的一个向量即可以简单地表示出一个矢量。与MATLAB、C++、Python等不同的是，Mathematica语言不需要为所有自定义变量赋予数据类型，并且可以进行符号、数值混合计算，大大减小了编程难度，基本上达到了即学即会的入门难度，方便学习《大学物理》课程的低年级学生掌握该编程语言。并且Mathematica还具有非常强大的三维作图能力，利用VectorPlot3D函数，我们可以很轻松地将(1)式用图像表示出来，如图1所示。从图中我们可以看到，不同空间位置处的矢量的方向和图表的大小不同，形象的表示出了静电场越靠近点电荷(0, 0, 0)电场强度越大，越远离电荷源，电场强度越低的特点，除此之外，我们还可以观察到静电场在空间中呈各向同性分布，具有球对称性。与其他数学模拟软件不同的是，Mathematica提供了强大的图形交互属性，学生可以通过鼠标调整该三维图形，从而达到从不同角度观察静电场性质的目的。

Figure 2. 2D vector and potential diagrams of electrostatic field generated by point charges in vacuum

图2. 真空中点电荷产生的静电场二维矢量图和电势图

Mathematica计算软件除了可以帮助学生理解三维情况下的静电场情况，还可以帮我们从其他视角来看待电场。如图2所示，在(a)中我们画出了 $z=0.5\text{m}$ 平面内的矢量场，而在(c)中我们可以画出 $z=5\text{m}$ 平面内的矢量场，通过对比不同位置处的矢量场，学生们可以自己得到结论：图2(a)中电场在圆心处(电荷正上方位置)较强，然后随着远离圆心后迅速衰减，整体规律和图1中非常符合；而在图2(c)中，电场虽然仍在圆心处(电荷正上方位置)最强，并且向四周衰减，但是其衰减程度远不如图2(a)中迅速，因此呈现出相对均匀的特点，这点也可以从电势图中看出。在图2(b)中，我们利用Mathematica软件绘出平面内的电势图，从中我们可以看到等势线相邻较密，根据电势和电场强度之间的关系，我们可以知道，等势线越密，电场强度变化的越快。同理，我们也在图2(d)中绘出了平面内的电势图，与图2(b)相比，等势线较为稀疏，根据上边的讨论，我们知道这意味着电场强度变化较慢，而这也正好符合图2(c)的结论。从这部分的模拟中，我们可以看到Mathematica可以帮助学生从电场强度、电势不同角度来看待同一问题，学生通过改变参数，比较不同情况下的不同结果，分析得出直观的结论，这使得学生由被动学习知识变为主动观察得到结论，更能激发学生的自主学习能力。

3. Mathematica在稳恒磁场中的应用

根据毕奥萨伐尔定律

$\text{d}B=\frac{{\mu }_0}{4\pi }\frac{I\text{d}l\times r}{r^3}$ (2)

可以计算电流源在真空中产生的稳恒磁场，但是毕奥萨伐尔定律是一个微分公式，如要计算整个电流源在空间中某一点的磁场需要对整个电流源进行积分，而被积函数是一个矢量函数，这对低年级的学生产生了比较大困扰，在传统课程中我们通常仅讨论具有比较高对称性的情形下的磁场，这大大限制了学生们对真实物理情况的理解。而Mathematica具有比较强的运算和画图能力可以弥补该缺点。这里我们以通电圆环为例，我们设通电圆环的半径为 $a=0.1\text{m}$ ，电流大小为 $I=1\text{A}$ ，我们把该圆环放在xoy平面内，并让圆心与O点重合，利用柱坐标，我们可以表示出

$B_x=\frac{{\mu }_0}{4\pi }{\displaystyle {\int }_0^{2\pi }\frac{Iaz\cos \beta }{\sqrt{a^2+{\rho }^2+z^2-2\rho az\cos \beta }}\text{d}\beta }$ (3)

$B_y=\frac{{\mu }_0}{4\pi }{\displaystyle {\int }_0^{2\pi }\frac{Iaz\sin \beta }{\sqrt{a^2+{\rho }^2+z^2-2\rho az\cos \beta }}\text{d}\beta }$ (4)

$B_z=\frac{{\mu }_0}{4\pi }{\displaystyle {\int }_0^{2\pi }\frac{Ia\left(a-\rho \cos \beta \right)}{\sqrt{a^2+{\rho }^2+z^2-2\rho az\cos \beta }}\text{d}\beta }$ (5)

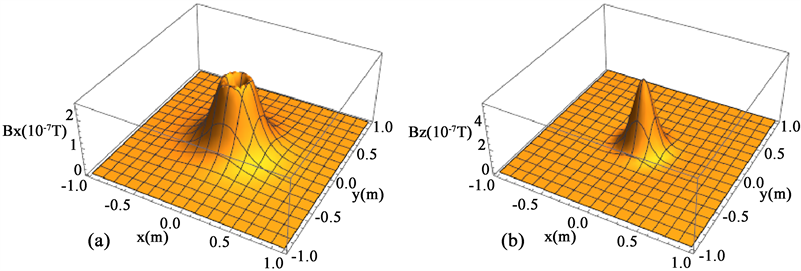
Figure 3. Stable magnetic field generated by annular current

图3. 环形电流产生的稳衡磁场

其中 $\rho =\sqrt{x^2+y^2}$ 。根究(3)式和(5)式，我们在图3(a)和图3(b)中分别画出了处的平行于x轴和z轴的磁感应强度分量，从图中可以看出磁感应强度随位置的变化关系。在两幅图中，磁感应强度呈圆对称分布，与电流分布情形相同，这从结果层面验证了我们在该部分化简处理时通常使用的圆对称性的合理性。其次，我们看到和的规律不同。其中，呈火山口的形状，中间凹陷，四周隆起，并且在的位置处达到极值，而则呈单峰状，在达到最大值。结合两幅图，我们可以得到在圆环的中轴线上，这与解析结果相同。通过这个例子，我们不难发现利用Mathematica计算模拟更有利于学生了解实际的物理情形，分析物理规律。

4. 总结

从上面的讨论中我们可以看到，Mathematica可以成为《大学物理》电磁学教学的一个重要工具，因其具有强大的矢量处理功能、简单的程序语言、兼具符号和数值计算的全能性等优点。通过对实际物理情形的建模，可以更加方便学生理解物理问题，拓展教材上的内容，提高授课效果。将计算模拟内容引入到大学物理课程中将使得学生在后续的课程中衔接更顺畅，提高了整个培养体系的效率。

基金项目

2023年沈阳航空航天大学本科教学改革研究项目：《大学物理》中计算模拟教学内容建设和实践；2021年度辽宁省普通高等教育本科教学改革研究优质教学资源建设与共享项目：依托跨校修读学分的大学物理线上线下混合式一流课程探索与建设；2022年辽宁省普通高等教育本科教学改革研究优质教学资源建设与共享项目：在混合式实验教学中开展跨校修读的探索与实践；2022年沈阳航空航天大学理学院教改项目：线上和线下混合式实验教学模式的探索和建设；2022年度辽宁省普通高等教育本科教学改革研究优质教学资源建设与共享项目：基于跨校修读的实践类课程创新教育引导及能力培养。