双圈图的补图的谱半径

The Spectral Radius of the Complement of Bicyclic Graphs

摘要: 设θ_n^*是将n−4条悬挂边粘到θ(2,1,2)的一个三度点得到的双圈图。本文我们证明了n个点的双圈图的补图的最大谱半径只在θ_n^*取到。

Abstract: Let θ_n^* be the bicyclic graph obtained by attaching n−4 pendant edges to a vertex of degree 3 on θ(2,1,2). In this paper we show that the maximum spectral radiu is achieved uniquely by θ_n^* among all complements of bicyclic graphs of order n.

1. 引言

设 $G\left(V,E\right)$ 是一个连通图，它的邻接矩阵 $A\left(G\right)$ 是一个 $\left(0,1\right)$ 实对称矩阵。所以它的特征值都是实数，从大到小的排序为： ${\lambda }_1\left(G\right)\ge {\lambda }_2\left(G\right)\ge \cdots \ge {\lambda }_n\left(G\right)$ ，其中最大的特征值 ${\lambda }_1\left(G\right)$ 为图G的谱半径，记为 $\rho \left(G\right)$ 。刻画图的谱半径的文章很多，诸如文献 [1] [2] [3] 等。刻画带限制条件的谱的文章也很多，例如在文献 [4] 中作者刻画了具有完美匹配的双圈图的谱半径，文献 [5] 中作者刻画了有n个点k个悬挂点的双圈图的谱半径。相对来说刻画图的补图的谱半径的文章还不太多，在文献 [6] 中作者刻画了单圈图的补图的谱半径。本文主要刻画了双圈图补图的谱半径，以及谱半径达到最大时的极图。在本文中我们假设图G和它的补图 $\bar{G}$ 都是连通的，定义矩阵 $A\left(\bar{G}\right)$ 的特征值 $\rho \left(\bar{G}\right)$ 对应的特征向量为 $x\left(\bar{G}\right)={\left(x_{v_1}\left(\bar{G}\right),x_{v_2}\left(\bar{G}\right),\cdots ,x_{v_n}\left(\bar{G}\right)\right)}^{\text{T}}$ ，其中 $x_{v_i}\left(\bar{G}\right)$ 是点 $v_i$ 对应的分量。

边数等于点数加一的连通图是双圈图。令 $C_n$ 和 $P_n$ 分别表示n个点的圈和路，我们定义图 $b\left(p,l,q\right)$ 是由两个点不交的圈 $C_p$ ， $C_q$ 和一条路 $P_l$ 组成的图形，其中 $P_l$ 的两个端点分别和 $C_p$ ， $C_q$ 有一个公共点，而当 $C_p$ 和 $C_q$ 有唯一的公共点时，我们记这个图形为 $b\left(p,0,q\right)$ 。定义图 $\theta \left(p,l,q\right)$ 为给定两个点中间连接有三条路 $P_{p+1}$ ， $P_{l+1}$ 和 $P_{q+1}$ ，其中这三条路两两之间除了两个给定的点外没有公共点。我们把 $b\left(p,l,q\right)$ 和 $b\left(p,0,q\right)$ 粘上一些树构成的图形记作 $B_n$ ，把 $\theta \left(p,l,q\right)$ 粘上一些树构成的图形记作 $\Theta \left(p,l,q\right)$ 。显然，所有n个点的双圈图由 $B_n$ 和 ${\Theta }_n$ 组成。

设 ${\theta }_n^{\ast }$ 是将 $n-4$ 条悬挂边粘到 $\theta \left(2,1,2\right)$ 的一个三度点得到的双圈图。本文我们证明了n个点的双圈图的补图的最大谱半径只在 ${\theta }_n^{\ast }$ 取到。

2. 主要结果

下面的定理在矩阵的研究中起到了非常重要的作用。

非负矩阵的Perron-Frobenius定理 [7] ：如果M是一个 $n\times n$ 阶的非负不可约矩阵，那么有以下结论成立：

i) 若 $\rho \left(M\right)$ 是矩阵A的最大特征值，则 $\rho \left(M\right)\ge 0$ ；

ii) $\rho \left(M\right)$ 是矩阵A的单重根；

iii) M有对应于特征值 $\rho \left(M\right)$ 的一个正的特征向量，使得 $Mx=\rho \left(M\right)x$ 。

众所周知图G是连通图的充分必要条件是图G对应的邻接矩阵是不可约的。

引理1 [6] 假设u和v是图G的两个不同的点， $\left\{v_i|i=1,2,\cdots ,s\right\}\subseteq N_G\left(v\right)\backslash \left(N_G\left(u\right)\cup \left\{u\right\}\right)$ ，其中 $N_G\left(v\right)$ 表示点v的邻点集。令 $G^{\ast }=G-{\displaystyle {\sum }_{1\le i\le s}{v}_{i}v}+{\displaystyle {\sum }_{1\le i\le s}{v}_{i}u}$ ，若 $x_u\left(\bar{G}\right)\le x_v\left(\bar{G}\right)$ ，则有 $\rho \left(\bar{G}\right)<\rho \left(\overline{G^{\ast }}\right)$ 成立。

假设u是图G的一个点， $T_l$ 是以v为根节点的一个l个点的树。我们将图G的u点和图 $T_l$ 的v点粘接成一个点得到的图形记作 $Guv{T}_l$ 。接下来用 $K_{1,l-1}$ 来表示以w为根节点的l个点的星图。由引理1容易得到下面的引理。

引理2 若图G， $T_l$ 和 $K_{1,l-1}$ 如上所定义，那么有 $\rho \left(\overline{Guv{T}_l}\right)\le \rho \left(\overline{Guw{K}_{1,l-1}}\right)$ ，其中等号成立的充分必要条件是 $Guv{T}_l\cong Guw{K}_{1,l-1}$ 。

引理3 [6] 假设图G和 $\bar{G}$ 都是连通的，uv是图G的一条非悬挂的割边，图G压缩边uv为一个点w并给w带一条悬挂边得到的图形记作图 $G^{\ast }$ ，那么有 $\rho \left(\bar{G}\right)<\rho \left(\overline{G^{\ast }}\right)$ 。

假设G与其补图 $\bar{G}$ 都是连通的。在接下来的内容里都用 $\bar{x}\left(G\right)={\left\{{\bar{x}}_v\left(G\right)|v\in V\left(G\right)\right\}}^{\text{T}}$ 表示 $A\left(\bar{G}\right)$ 的对应于 $\rho \left(\bar{G}\right)$ 的特征向量，其中 ${\bar{x}}_v\left(G\right)$ 对应点v。

定理4 若 $G\in B_n$ ，u是G的子图 $b\left(3,0,3\right)$ 的4度点，则 $\rho \left(\bar{G}\right)\le \rho \left(\overline{b\left(3,0,3\right)uw{K}_{1,n-5}}\right)$ ，当且仅当 $G\cong b\left(3,0,3\right)uw{K}_{1,n-5}$ 时等号成立。

证明：令 $G\in B_n$ 使得它的补图 $\bar{G}$ 具有极大的谱半径。

首先我们来证明 $b\left(p,0,q\right)$ 是图G的子图。

假设图G的子图是 $b\left(p,l,q\right)$ ，其中 $l\ge 1$ ， $P_{l+1}=u_1{u}_2\cdots u_{l+1}$ 是连接两个圈 $C_p$ 和 $C_q$ 的路，其中 $u_1\in V\left(C_p\right)$ ， $u_{l+1}\in V\left(C_q\right)$ 。

如果 $x_{u_1}\left(\bar{G}\right)\ge x_{u_l}\left(\bar{G}\right)$ ，令

$G_1=G-u_{1}w+u_{l}w$

如果 $x_{u_1}\left(\bar{G}\right)\le x_{u_l}\left(\bar{G}\right)$ ，令

$G_1=G-u_l{w}^{\prime }+u_1{w}^{\prime }$

其中 $w\in C_p\cap N_G\left(u_1\right)$ ， $w^{\prime }\in C_q\cap N_G\left(u_l\right)$ 。显然 $G_1,G_2\in B_n$ ，由引理1有 $\rho \left(\overline{G_1}\right)>\rho \left(\bar{G}\right)$ 且 $\rho \left(\overline{G_2}\right)>\rho \left(\bar{G}\right)$ ，这与 $\bar{G}$ 有极大的谱半径相矛盾，故 $l=0$ ，因此 $b\left(p,0,q\right)$ 是图G的子图。

其次我们证明图G只有一个树子图，并且它以G的两个圈唯一的公共点u为根节点。

假设点v是图G的一个树子图 $T_1$ 的根节点，其中 $v\in C_p$ 并且 $v\ne u$ 。

如果 $x_u\left(\bar{G}\right)\ge x_v\left(\bar{G}\right)$ ，令

$G_3=G-{\displaystyle \underset{w\in N_G\left(u\right)\cap T_1}{\sum }uw}+{\displaystyle \underset{w\in N_G\left(u\right)\cap T_1}{\sum }vw}$

如果 $x_u\left(\bar{G}\right)\le x_v\left(\bar{G}\right)$ ，令

$G_4=G-{\displaystyle \underset{w^{\prime }\in N_G\left(v\right)\cap C_q}{\sum }u{w}^{\prime }}+{\displaystyle \underset{w^{\prime }\in N_G\left(v\right)\cap C_q}{\sum }u{w}^{\prime }}$

显然 $G_3,G_4\in B_n$ ，由引理1有 $\rho \left(\overline{G_3}\right)>\rho \left(\bar{G}\right)$ 且 $\rho \left(\overline{G_4}\right)>\rho \left(\bar{G}\right)$ ，这与 $\bar{G}$ 有极大的谱半径相矛盾，因此 $v=u$ 。继续上述过程我们可以证得图G只有一个树子图，并且它的根节点为图G的圈上的4度点u。

由引理3很容易证明接在点u出的树是一个星子图。

最后我们证明两个圈 $C_p$ 和 $C_q$ 都是3长圈。

不失一般性，假设 $p\ge 4$ ，并且 $C_p=u_1{u}_2\cdots u_p{u}_1$ 。

如果 $x_{u_1}\left(\bar{G}\right)\le x_{u_2}\left(\bar{G}\right)$ ，令

$G_5=G-u_2{u}_3+u_1{u}_3$

如果 $x_{u_1}\left(\bar{G}\right)\ge x_{u_2}\left(\bar{G}\right)$ ，令

$G_6=G-{\displaystyle \underset{u\in N_G\left(u_1\right)\backslash \left\{u_2\right\}}{\sum }{u}_{1}u}+{\displaystyle \underset{u\in N_G\left(u_1\right)\backslash \left\{u_2\right\}}{\sum }{u}_{2}u}$

显然 $G_5,G_6\in B_n$ ，由引理1有 $\rho \left(\overline{G_5}\right)>\rho \left(\bar{G}\right)$ 且 $\rho \left(\overline{G_6}\right)>\rho \left(\bar{G}\right)$ ，这与 $\bar{G}$ 有极大的谱半径相矛盾，因此 $p=3$ ，同理可证得 $q=3$ 。

综上所述，如果 $G\in B_n$ ，要使得 $\bar{G}$ 极大，则必有 $G\cong b\left(3,0,3\right)uw{K}_{1,n-5}$ 。 □

定理5若 $G\in {\Theta }_n$ ，则有 $\rho \left(\bar{G}\right)\le \rho \left(\overline{\theta \left(2,1,2\right)uw{K}_{1,n-4}}\right)$ ，其中点u是图G的子图 $\theta \left(2,1,2\right)$ 的3度点，等号成立的充要条件是 $G\cong \theta \left(2,1,2\right)uw{K}_{1,n-4}$ 。

证明：令 $G\in {\Theta }_n$ 使得它的补图 $\bar{G}$ 有极大的谱半径。

首先我们来证明图G只有一个树子图。

假设 $T_1$ 和 $T_2$ 是图G的两个树子图，它们分别以 $\theta \left(p,l,q\right)$ 上的点u和v为根节点。

如果 $x_u\left(\bar{G}\right)\ge x_v\left(\bar{G}\right)$ ，令

$G_7=G-{\displaystyle \underset{u^{\ast }\in N_G\left(u\right)\cap T_1}{\sum }{u}^{\ast }u}+{\displaystyle \underset{u^{\ast }\in N_G\left(u\right)\cap T_1}{\sum }{u}^{\ast }v}$

如果 $x_u\left(\bar{G}\right)\le x_v\left(\bar{G}\right)$ ，令

$G_8=G-{\displaystyle \underset{u^{\ast }\in N_G\left(v\right)\cap T_2}{\sum }{u}^{\ast }v}+{\displaystyle \underset{u^{\ast }\in N_G\left(u\right)\cap T_1}{\sum }{u}^{\ast }u}$

显然 $G_7,G_8\in B_n$ ，由引理1有 $\rho \left(\overline{G_7}\right)>\rho \left(\bar{G}\right)$ 且 $\rho \left(\overline{G_8}\right)>\rho \left(\bar{G}\right)$ ，这与 $\bar{G}$ 有极大的谱半径相矛盾，继续上述过程可知图G只含有一个树子图。

由引理3很容易证明接在点u出的树是一个星子图，我们记该树子图的根节点为 $u_1$ 。

接下来我们证明 $\theta \left(l,p,q\right)\cong \theta \left(2,1,2\right)$ 。

假设 $l\ge 3$ ，并且 $P_{l+1}=u_1{u}_2\cdots u_{l+1}$ 。

如果 $x_{u_1}\left(\bar{G}\right)\le x_{u_2}\left(\bar{G}\right)$ ，令

$G_9=G-u_2{u}_3+u_1{u}_3$

如果 $x_{u_1}\left(\bar{G}\right)\ge x_{u_2}\left(\bar{G}\right)$ ，令

$G_{10}=G-{\displaystyle \underset{u^{\ast }\in N_G\left(u_1\right)\backslash \left\{u_2\right\}}{\sum }{u}^{\ast }{u}_1}+{\displaystyle \underset{u^{\ast }\in N_G\left(u_1\right)\backslash \left\{u_2\right\}}{\sum }{u}^{\ast }{u}_2}$

显然 $G_9,G_{10}\in B_n$ ，由引理1有 $\rho \left(\overline{G_9}\right)>\rho \left(\bar{G}\right)$ 且 $\rho \left(\overline{G_{10}}\right)>\rho \left(\bar{G}\right)$ ，这与 $\bar{G}$ 有极大的谱半径相矛盾，继续上述过程我们可以得到 $l\le 2$ ，同理可以证得 $p\le 2$ ， $q\le 2$ ，由双圈图的定义可知l，p和q最多有一个为1。不失一般性我们令 $l=1$ 。因此 $\theta \left(l,p,q\right)\cong \theta \left(2,1,2\right)$ 。

若 $d_G\left(u_1\right)=2$ ，则 $G\cong {\theta }_n^{\ast }$ ，若 $d_G\left(u_1\right)=3$ ，则 $G\cong {\theta }_n^{\ast \ast }$ ，如图1所示。

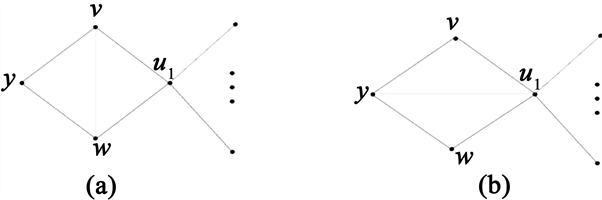
Figure 1. (a) ${\theta }_n^{\ast }$ ; (b) ${\theta }_n^{\ast \ast }$

图1. (a) ${\theta }_n^{\ast }$ ；(b) ${\theta }_n^{\ast \ast }$

最后我们证明 $G\cong {\theta }_n^{\ast \ast }$ 。

用反证法，假设 $d_{u_1}\left(G\right)=3$ ，比较 $x_{u_1}\left(\bar{G}\right)$ 和 $x_v\left(\bar{G}\right)$ 的大小。

如果 $x_{u_1}\left(\bar{G}\right)\ge x_v\left(\bar{G}\right)$ ，令

$G_1^{\ast }=G-{\displaystyle \underset{u^{\ast }\in N_G\left(u_1\right)\backslash \left\{v,w\right\}}{\sum }{u}^{\ast }{u}_1}+{\displaystyle \underset{u^{\ast }\in N_G\left(u_1\right)\backslash \left\{v,w\right\}}{\sum }{u}^{\ast }{u}_1}$

如果 $x_{u_1}\left(\bar{G}\right)\le x_v\left(\bar{G}\right)$ ，令

$G_2^{\ast }=G-vy+y{u}_1$

显然 $G_1^{\ast },G_2^{\ast }\in {\Theta }_n$ ，且 $G_1^{\ast }$ 和 $G_2^{\ast }$ 均与 ${\theta }_n^{\ast \ast }$ 同构。由引理1有 $\rho \left(\overline{G_1^{\ast }}\right)>\rho \left(\bar{G}\right)$ 且 $\rho \left(\overline{G_2^{\ast }}\right)>\rho \left(\bar{G}\right)$ ，这与 $\bar{G}$ 有极大的谱半径相矛盾。 □

定理6 假设G是一个n个点的连通的双圈图，则 $\rho \left(\bar{G}\right)\le \rho \left(\overline{{\theta }_n^{\ast \ast }}\right)$ ，当且仅当 $G\cong {\theta }_n^{\ast \ast }$ 时等号成立。其中 ${\theta }_n^{\ast \ast }$ 如图1所示。

证明：令v是图G的子图 $b\left(3,0,3\right)$ 的4度点，由定理4.2.4和定理4.2.5可知在双圈图中我们只需证明 $\rho \left(\overline{b\left(3,0,3\right)vw{K}_{1,n-5}}\right)<\rho \left(\overline{\theta \left(2,1,2\right)uw{K}_{1,n-4}}\right)$ 即可。

令 $H_1=b\left(3,0,3\right)vw{K}_{1,n-5}$ ， $H_2=\theta \left(2,1,2\right)uw{K}_{1,n-4}$ 。则有

$P\left(\overline{H_1};\lambda \right)=\left|I\lambda -A\left(\overline{H_1}\right)\right|={\lambda }^3{\left(\lambda +1\right)}^{n-6}\left(\lambda +2\right)\left({\lambda }^2+\left(4-n\right)\lambda +2\left(4-n\right)\right)$

$P\left(\overline{H_2};\lambda \right)=\left|I\lambda -A\left(\overline{H_2}\right)\right|=\lambda {\left(\lambda +1\right)}^{n-4}\left({\lambda }^3+\left(4-n\right){\lambda }^2+\left(7-2n\right)\lambda +n-4\right)$

因为实对称矩阵的特征值非负，所以 $\rho \left(\overline{H_1}\right)=\frac{n-4+\sqrt{n^2-16}}{2}$ 。

令 $f\left(x\right)=x^3+\left(4-n\right)x^2+\left(7-2n\right)x+n-4$ ，则 $f^{\prime }\left(x\right)=3x^2+2\left(4-n\right)x+7-2n$ 。

如果 $x>\frac{n-4+\sqrt{n^2-2n-5}}{3}$ ，则有 $f^{\prime }\left(x\right)>0$ ，因此当 $x>\frac{n-4+\sqrt{n^2-2n-5}}{3}$ 时 $f\left(x\right)$ 是个增函数。显然 $\frac{n-4+\sqrt{n^2-16}}{2}>\frac{n-4+\sqrt{n^2-2n-5}}{3}$ ，并且

$\begin{array}{c}f\left(\frac{n-4+\sqrt{n^2-16}}{2}\right)={\left(\frac{n-4+\sqrt{n^2-16}}{2}\right)}^3+\left(4-n\right){\left(\frac{n-4+\sqrt{n^2-16}}{2}\right)}^2\\ +\left(7-2n\right)\left(\frac{n-4+\sqrt{n^2-16}}{2}\right)+n-4\\ =\frac{n-4-\sqrt{n^2-16}}{2}<\frac{n-4-\sqrt{{\left(n-4\right)}^2}}{2}=0\end{array}$

因为 $\rho \left(\overline{H_2}\right)$ 是方程 $f\left(x\right)$ 的一个根，所以 $\rho \left(\overline{b\left(3,0,3\right)vw{K}_{1,n-5}}\right)<\rho \left(\overline{\theta \left(2,1,2\right)uw{K}_{1,n-4}}\right)$ 成立。 □

基金项目

新疆自治区研究生创新项目(XJ2021G253)。

NOTES

^*通讯作者。