煤粉炉水冷刮板式干排渣技术研究

Research on Dry Slagging Technique of Water-Cooled Scraper in Pulverized Coal Furnace

摘要: 由于我国水资源短缺国情，干排渣技术得到提倡，但风冷式干排渣导致的炉底漏风问题无法避免。为避免漏风问题，提出一种新型间接水冷干排渣方式，采用数值模拟的方法研究了新排渣方式下，底渣的运动状态和冷却效果，对比了新排渣方式和传统排渣方式的优缺点，结果表明：新排渣方式在运输灰渣的同时加强了灰渣颗粒之间的混合，排渣温度更均匀，由于换热面积的降低导致降温效果略微低于钢带式运输方式，但仍满足运输阶段的排渣冷却，灰渣温度从523.15 K降低到449.9 K。新排渣结构下，冷却水流速高于0.5 m/s后排渣温度不再显著降低。

Abstract: Due to the shortage of water resources in our country, dry slag technology is advocated, but air leakage caused by air-cooled dry slagging system is unavoidable. In order to avoid air leakage, a new indirect water-cooled dry slagging method is proposed. Numerical simulation is used to study the motion state and cooling effect of bottom slagging under the new slagging method, and the advantages and disadvantages of the new slagging method and the traditional slagging method are compared. The results show that the new slagging method strengthens the mixing between ash particles while transporting ash, and the slagging temperature is more uniform. The cooling effect is slightly lower than that of the steel belt transportation method due to the reduction of heat exchange area, but it still satisfies the slagging cooling in the transportation stage, and the ash temperature decreases from 523.15 K to 449.9 K. Under the new slag discharge structure, the slag temperature no longer decreases significantly after the cooling water flow velocity is higher than 0.5 m/s.

1. 引言

目前煤粉锅炉常用的排渣系统有湿排渣和干排渣两种。由于冷却介质不同，再由我国水资源短缺的国情出发，干排渣技术得到提倡。但风冷式干排渣中冷渣空气被认为是炉底漏风，属于无序漏风。在控制炉膛出口过剩空气系数不变的情况下，冷却风量的增加导致通过空气预热的一次风量减少，因此这种泄漏影响燃烧条件和排烟温度 [1] 。刘铭媛 [2] 指出在6%漏风量情况下，炉底漏风全部由燃尽风弥补时，漏风对燃烧过程影响很小，但由二次风弥补时，会严重影响燃烧过程，火焰中心上升，煤粉燃尽推迟，减温水量增加。许多学者的研究 [3] [4] 表明，将冷却风量控制在锅炉所需风量的1%以下可以忽略其对炉膛燃烧的影响。对于锅炉效率而言，何彦鹏 [5] 等研究发现：当冷却风量小于0.45%才能够保证MAC系统对锅炉影响较小，当冷却风量比例增加时，锅炉效率也会降低。风冷式排渣系统在大排渣量下灰渣处理能力不足，一部分由于冷却风量不能太大而影响原先设计的烟风系统；一部分由于灰渣堆积，被覆盖在中心的灰渣难以将热量传递给空气。

目前也有学者提出排渣废热的回收应用。黄嘉驷 [6] 等人分析了冷渣水回水节点对机组整体循环效率的影响。李慧君 [7] 等人提出采用有机朗肯循环(ORC)余热发电技术回收排渣废热。更有学者提出与煤气化行业联合 [8] 。对于排渣废热的应用研究较多，但如何在煤粉炉中实现这一过程却少有提及。

本文提出一种间接水冷的排渣方式。采用刮板运输机运输灰渣颗粒，这样可以避免风冷式钢带运输机与灰渣摩擦力不够而引起的输渣能力不足问题，还可以使灰渣颗粒在运输过程中产生相对位移，更好的被冷却。在回收排渣废热的同时，不影响炉膛燃烧条件和排烟温度。

2. 模型构建

思路源于炉膛水冷壁，运输灰渣的设备由钢带式运输机改变为刮板式运输机，运输机的底板由类似于水冷壁结构的钢结构代替，如图1所示。

拟采用24根平行管路来组成1.32 m宽的运输轨道，刮板间距0.324 m，运输速度0.046 m/s。在排渣量5.46 t/h的工况下，单根管子、两个刮板内的灰渣量为0.4451 kg。灰渣物性均采用真实物性，来源于电厂技术协议和文献 [9] [10] 数据插值得到，展示于表1。

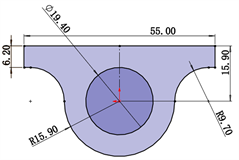
(a)整体结构图 (b)截面结构图

Figure 1. Illustrative diagram of model structure

图1. 模型结构说明图

Table 1. Physical properties of ash and steel structures

表1. 灰渣和钢结构的物性表

3. 数学模型及网格无关验证

3.1. 数学模型

3.1.1. 颗粒运动及换热计算模型

EDEM采用离散元的数值模拟方法，灰渣颗粒之间的作用采用Hertz-Mindlin (no slip)模型来计算。在这个模型中，法向力成分是基于赫兹接触理论。切向力模型是基于Mindlin-Deresiewicz的工作。法向力和切向力都有阻尼成分，其中阻尼系数与恢复系数有关，切向摩擦力遵循库仑摩擦定律模型，滚动摩擦力以独立于接触的方向性恒定扭矩模型实现。具体计算公式如下：

法向力是重合度的函数：

$F_n=\frac{4}{3}{E}^{*}\sqrt{r^{*}}{\delta }_n^{\frac{3}{2}}$ (1)

式中 ${\delta }_n$ 是法线重合度；E^*是有效杨氏模量；r^*是平均粒径，定义分别如下：

$\frac{1}{E^{*}}=\frac{\left(1-w_i^2\right)}{E_i}+\frac{\left(1-w_j^2\right)}{E_j}$ (2)

$\frac{1}{r^{*}}=\frac{1}{R_i}+\frac{1}{R_j}$ (3)

式中E，w，R分别为杨氏模量、泊松比和半径。另外法线阻尼力通过下式给出：

$F_n^d=-2\sqrt{\frac{5}{6}}\beta \sqrt{S_n{m}^{*}}{v}_n^{\stackrel{\to }{rel}}$ (4)

式中m^*是等效质量； $v_n^{\stackrel{\to }{rel}}$ 是相对速度的法线分量，m^*和 $\beta$ 和S_n的定义如下：

$m^{*}={\left(\frac{1}{m_1}+\frac{1}{m_i}\right)}^{-1}$ (5)

$\beta =\frac{-\ln e}{\sqrt{{\ln }^{2}e+{\pi }^2}}$ (6)

$S_n=2E^{*}\sqrt{R^{*}{\delta }_n}$ (7)

式中e是恢复系数。切向力F_t取决于切向重叠度 ${\delta }_{\text{t}}$ 和切线刚度S_t：

$F_t=-S_t{\delta }_t$ (8)

$S_t=8G^{*}\sqrt{R^{*}{\delta }_n}$ (9)

式中G^*是等效剪切模量，切向阻尼由下式给出：

$F_t^d=-2\sqrt{\frac{5}{6}}\beta \sqrt{S_t{m}^{*}}{v}_t^{\stackrel{\to }{rel}}$ (10)

式中 $v_t^{\stackrel{\to }{rel}}$ 是相对切向速度，切向力受摩擦力的限制，最后，颗粒总的受力用合力计算：

$F={\displaystyle \sum F_n}+{\displaystyle \sum F_t}$ (11)

颗粒滚动的计算，滚动摩擦的计算是通过在壁面加扭矩来体现的，计算公式如下：

${\tau }_i=-{\mu }_r{F}_n{R}_i{\omega }_i$ (12)

式中 ${\mu }_r$ 是滚动摩擦系数，R是接触点与质心的距离， ${\omega }_i$ 是接触点上物体的单位角速度矢量。

颗粒的温度会随热通量的计算而改变从而实现温度的传递，定义如下：

$Q_{p1p2}=h_c\Delta T_{p1p2}$ (13)

接触面积的作用表现在传热系数中，并由下列公式给出：

$h_c=\frac{4k_{p1}{k}_{p2}}{k_{p1}+k_{p2}}{\left[\frac{3F_N{r}^{*}}{4E^{*}}\right]}^{1/3}$ (14)

式中F_N是法向力，N。

颗粒的温度更新通过以下公式计算：

$m_p{C}_p\frac{\text{d}T}{\text{d}t}={\displaystyle \sum Q_{heat}}$ (15)

3.1.2. 等效介质假设法计算模型

整个运输过程的换热通过Fluent软件实现，主要方程如下

连续性方程：

$\frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho v\right)=0$ (16)

式中r代表密度，kg/m³；t代表时间，s； $v$ 是速度矢量，m/s。

动量方程：

$\frac{\partial }{\partial t}\left(\rho v\right)+\nabla \cdot \left(\rho vv\right)=-\nabla p+\nabla \cdot \left(\tau \right)+\rho g$ (17)

$\tau =\mu \left[\left(\nabla v+\nabla v^{{\rm T}}\right)-\frac{2}{3}\nabla \cdot vI\right]$ (18)

式中p代表压力，Pa；g代表重力加速度m/s²； $\tau$ 代表应力张量； $\mu$ 是粘度，kg/(m·s)。

能量方程：

$\frac{\partial }{\partial t}\left(\rho H\right)+\frac{\partial }{\partial x_i}\left[u_i\left(\rho H+p\right)\right]=\frac{\partial }{\partial x_j}\left(k_{eff}\frac{\partial T}{\partial x_j}\right)+S_h$ (19)

$k_{eff}=k+\frac{c_p{\mu }_t}{{\mathrm{Pr}}_t}$ (20)

式中H代表总能，k_eff表示湍流有效导热系数，W/(m·k)；T表示温度，K；S_h代表源项， ${\mu }_t$ 表示湍流粘度，kg/(m·s)； ${\mathrm{Pr}}_t$ 表示湍流普朗特数。

本文使用Realizable k-e模型进行计算，Y⁺的范围是0~300，选择增强型壁面处理近壁函数。相关计算公式如下：

$\frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial x_j}\left(\rho k{u}_j\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]+G_k-\rho \epsilon$ (21)

$\frac{\partial }{\partial t}\left(\rho \epsilon \right)+\frac{\partial }{\partial x_j}\left(\rho \epsilon u_j\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\frac{\partial \epsilon }{\partial x_j}\right]+\rho C_{1}S\epsilon -\rho C_2\frac{{\epsilon }^2}{k+\sqrt{v\epsilon }}$ (22)

式中k表示湍流动能，m²/s²；ε表示湍流动能耗散率，m³/s²；G_k表示由于平均速度梯度而产生的湍流动能；S表示平均应变速率的模数；C2是常数，其值为1.9； ${\sigma }_k$ 和 ${\sigma }_e$ 是k和e的经验值，其值分别为1.0和1.2。

对于固体域，只计算能量方程，因为连续性方程和动量方程自动满足。能量方程如下：

$\frac{\partial }{\partial t}\left(\rho h\right)+\nabla \cdot \left(\rho hv\right)=\nabla \cdot \left(k\nabla T\right)+S_t$ (26)

式中h表示显焓，J/kg；S_t表示体积热源项，W/m³；左面第二项是对流项，是由于固体移动产生的。

在稳态条件下运行时，灰渣温度可以看作不随时间变化，所以模拟采用伪瞬态Couple算法。压力使用PRESTO格式，动量、能量和湍流耗散率使用QUICK格式。二阶迎风格式用于湍流动能。为确保计算结果收敛，监测底灰的温度变化，直到稳定。

3.2. 网格无关性验证

网格无关性验证是做模拟不可缺少的一步，根据软件不同验证的需求程度也不同。单纯EDEM软件的模拟计算不需要进行网格验证，该软件的网格用来检索灰渣颗粒及其接触状态，一般取颗粒半径的2~3倍，本文取3倍颗粒半径，时间步长取1.64e^–6。所以本节针对使用Fluent模拟换热过程的间接水冷结构进行网格无关性验证，如图2。当网格数量大于42万时，冷却水的出口温度和排渣温度不再大幅度变化，所以本文选取59万网格作为模拟使用的网格。

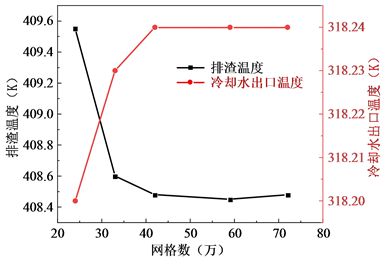
Figure 2. Pipe heat exchange grid irrelevance verification diagram

图2. 管道换热网格无关性验证图

4. 结果与讨论

4.1. 运动过程分析

颗粒运动模拟参考滚筒冷渣器内颗粒运动研究 [11] [12] 。钢带式运输机和刮板式运输机颗粒运动情况如图3。

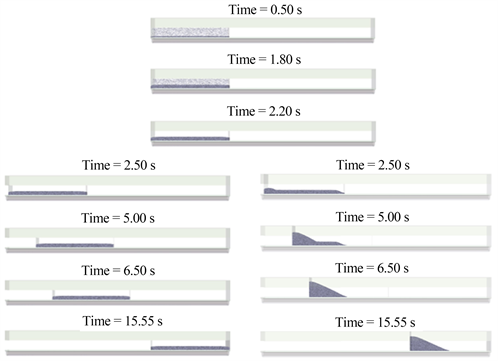
Figure 3. Ash particle movement diagram (steel belt conveyor (left) scraper conveyor (right))

图3. 灰渣颗粒运动图(钢带式运输机(左)刮板式运输机(右))

前2.2 s灰渣掉落堆积，运输机不工作，两种运输方式的颗粒状态相同，2.2 s颗粒生成完成，运输机开始运行，直到15.55 s模拟结束。通过钢带式运输机运输灰渣时，灰渣颗粒之间没有相对位移，一直保持一定的厚度移动；通过刮板运输机运输灰渣的过程中，2.2 s到6.5 s之间，随着刮板的移动，右侧颗粒失去了刮板的支撑，坍落成自然堆积状态，左侧颗粒在刮板的推动作用下，逐渐堆积，颗粒从平铺状态变成左高右低的状态，到6.5 s以后，灰渣堆积成固定形状，以固定的堆积高度和堆积角度随着刮板一起向前移动，堆积高度约为74.10 mm，堆积角度约为26.92˚。6.5 s以后刮板运输机中灰渣运动状态看似规律，但颗粒运动十分复杂。

紧靠刮板和底板的区域，这里的颗粒被挤压逐渐向上移动，而灰渣之间的摩擦小于灰渣与两侧挡板的摩擦，加上重力作用，导致这些颗粒向中间靠拢；位于最高位置的颗粒有的保持高度随刮板直线运动，有些被挤压到斜面区域然后滚落到底板。

图4和图5分别显示了刮板式运输机两个挡板中心截面和挡板附近的颗粒运动状态，速度高于0.08 m/s的颗粒用红色表示，小于0.02 m/s的颗粒用蓝色表示。中心截面的颗粒明显分成三个区域，底板附近的颗粒移动速度小于刮板移动速度，可以看成类似静止区，斜面部位红色区域是滚落区，还有中间和刮板运行速度相差不大的移动区。挡板附近颗粒移动十分混乱，在底板附近有更大范围的类似静止区，在颗粒内部不仅出现了许多速度小于0.02 m/s的区域，还出现了个别速度大于0.08 m/s的颗粒，这是颗粒受重力，挤压，摩擦共同作用的结果。从6.5 s到15.55 s，颗粒保持这种状态向前移动。

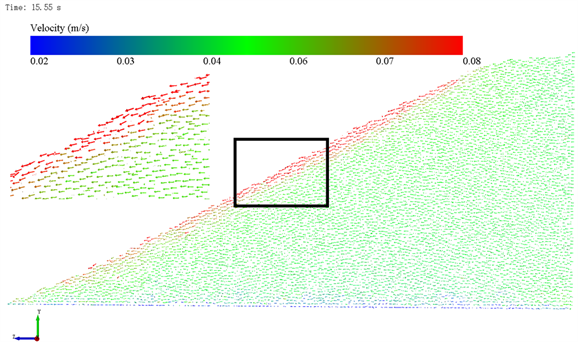
Figure 4. Movement of particles in the central section

图4. 中心截面颗粒的运动状态

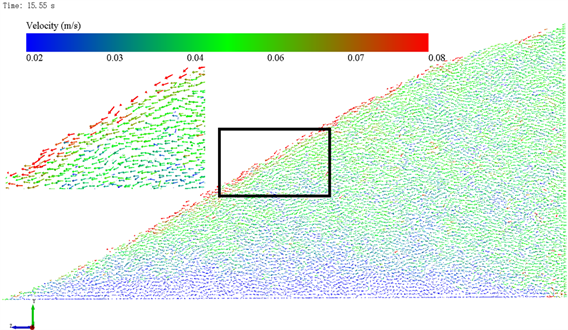
Figure 5. Movement of particles in the cross section near the baffle

图5. 挡板附近截面颗粒的运动状态

4.2. 换热分析

钢带式运输机中灰渣的冷却过程及局部放大图如图6，最上层灰渣得不到冷却，温度难以传递到底板，所以排渣过程中灰渣的最高温度保持初始温度不变，最下层灰渣一直受凝结水的间接冷却，最低温度随时间一直降低，从523.15 K降低到431.74 K。整体温度分布呈现上高下低的趋势，类似于非稳态导热温度分布。刮板式运输机中灰渣的冷却过程及不同视角局部放大图如图7。相比于钢带式运输机，刮板式运输机使灰渣之间相互混合，颗粒的运动轨迹不是一条水平线，灰渣颗粒之间的温差更小、温度更均匀，最大温差只有52.56 K。灰渣颗粒最高温度同样一直不变，一部分是由于模拟时间短；一部分由于颗粒混合效果并不均匀，刮板不能保证所有灰渣颗粒都能够与底板接触。最低温度呈现先降低后升高的趋势，到11.3 s时灰渣颗粒达到最低温度，之后颗粒最低温度上升，说明11.3 s后，一开始被堆积在下面的灰渣颗粒被挤压到更高的位置，这些灰渣颗粒开始得不到底板的冷却，开始受周围更高温度的灰渣颗粒加热。

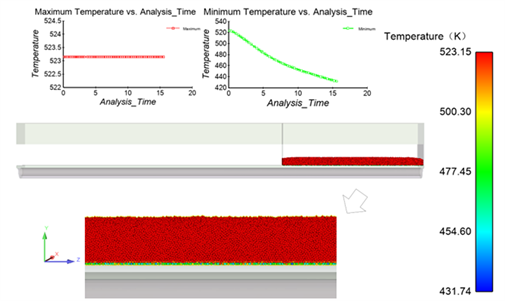
Figure 6. Temperature distribution of ash particles in steel belt conveyor

图6. 钢带式运输机灰渣颗粒温度分布图

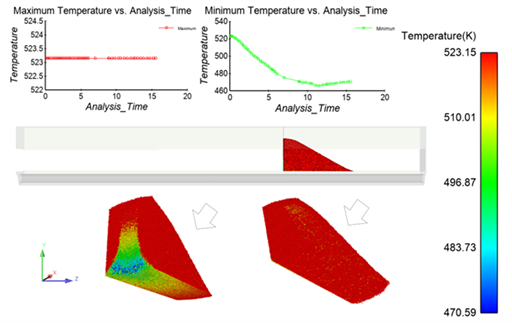
Figure 7. Temperature distribution of ash particles in scraper conveyor

图7. 刮板式运输机灰渣颗粒温度分布图

表2为刮板式运输机和钢带式运输机排渣冷却效果对比，同样冷却时长，钢带运输机降温2.35 K，刮板运输机降温1.51 K，降温效果降低35.74%。这是由于刮板运输形式使灰渣与底板的接触面积降低，根据模拟结果，刮板式运输机灰渣投影到底板的面积为90.20 cm²，仅为钢带式运输机灰渣投影到底板面积的50.62%。数值上来看，刮板运输机在同样换热面积下，具备更好的冷却条件，如果采用合适的排渣方式弥补这一缺陷，刮板运输机将会有更好的冷却效果。刮板推动灰渣运动可以使中心高温颗粒接触冷却底板，增加换热温差，有类似破坏温度边界层的功能。

Table 2. Comparison table of cooling effect

表2. 降温效果对比表

整体排渣过程的冷却通过Fluent软件模拟，进口位置的灰渣温度为某热电厂现场测量温度，通过等效介质假设模拟灰渣在整个运输阶段的降温，灰渣的堆积参数及其他模拟条件如表3所示。

Table 3. Physical properties parameters

表3. 物性参数

在仅考虑锅炉给水的间接冷却条件下，保守地估计新结构对灰渣的降温效果。同样的冷却时间下，灰渣可以最低被冷却到408.45 K，灰渣温度降低了114.7 K，对比校验后应用刮板式运输机可以使灰渣降温73.25 K，所以排渣温度约为449.9 K，满足冷却灰渣的要求。

图8显示了冷却水流速0.3 m/s时钢结构的截面随轴向的温度变化情况。Z变大方向为灰渣的移动方向。钢结构内部的温度分布呈对称趋势，与水冷壁温度分布相似，距离冷却水越近的地方，温度越低。最低温度一直出现在钢结构的最底部，距离冷却水最远的地方温度最高。随着灰渣的移动，钢结构截面的温差越来越小，最后接近冷却水进口温度。Z = 0.2 m处的钢结构的最高温度和最低温度差距最大，因为此处灰渣与底板换热最强烈。

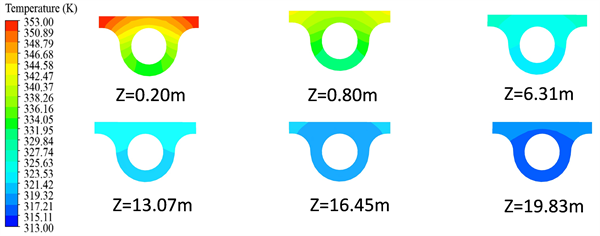
Figure 8. Indirect water-cooled steel structure temperature distribution with position

图8. 间接水冷钢结构温度分布随位置变化图

图9说明了冷却水流量与排渣温度的关系，当冷却水流速高于0.5 m/s时，增加冷却水流量不会对排渣温度造成明显影响。值得注意的是冷却水流速等于0.1 m/s时，冷却水出口温度达到了360.95 K。这说明排渣可以作为加热厂内生活用水和热网回水的热量来源。这也说明排渣废热有产生蒸汽的能力，可以与有机朗肯循环结合以产生更高品位的能量。

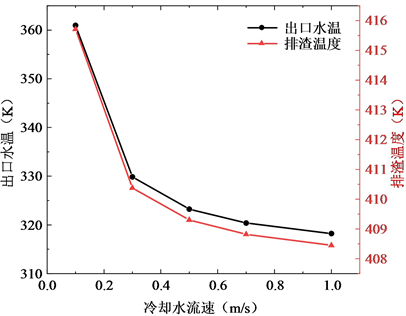
Figure 9. Indirect water-cooled cooling effect with cooling water flow rate

图9. 间接水冷冷却效果随冷却水流速变化图

5. 结论

1) 刮板运输机可以有效的使中心灰渣与冷源接触，排渣温度更均匀，不会产生钢带式运输中出现的温度分层现象，但由于其工作特点，导致灰渣与底板的接触面积减少了49.38%，所以整体冷却效果不及同冷却条件下的钢带式运输机，在运输段进口温度523.15 K的情况下，可以降温73.25 K，排渣温度约为449.9 K，基本满足运输过程中排渣的冷却要求。

2) 冷却水管的温度分布各截面趋势相同，底部温度低，肋片处温度高，延灰渣移动方向，冷却水管截面温差越来越小，越来越接近冷却水温度。

基金项目

国家自然科学基金项目(52072081)。