Laplace分布参数的Bayes统计推断研究

A Study of Bayes Statistical Inference for Parameter of Laplace Distribution

摘要: Laplace分布在金融研究、可靠性理论、机器学习中具有重要的作用。本文将讨论Laplace分布参数的Bayes统计推断问题。首先研究了Laplace分布参数在平方误差损失、LINEX损失和熵损失这三类损失函数下的Bayes估计问题，然后研究了基于平方误差损失函数下的风险函数的比较问题，并通过蒙特卡洛模拟考察了各类估计的优良性，最后提出在实际应用Bayes估计时，如何针对n的取值来选择合适的Bayes估计。

Abstract: Laplace distribution plays an important role in financial research, reliability theory, and machine learning. This paper will discuss the Bayes statistical inference of Laplace distribution parameters. Firstly, the Bayes estimation of the distribution parameter under scale squared error loss, LINEX loss and entropy loss is studied, and then the comparison of risk functions under square error loss function is studied and the advantages of various estimates are investigated by Monte Carlo simula-tion. Finally, how to select an appropriate Bayes estimation based on the value of n is proposed in practical application of Bayes estimation.

1. 引言

Laplace分布由两个指数函数组成的，所以又叫做双指数函数分布(double exponential distribution)，在金融工程、质量控制和机器学习等领域中有着重要的应用。Laplace分布的密度函数曲线具有尖峰和重尾特征，这可以很好地刻画金融数据 [1] [2] 。文献 [3] 用非对称Laplace分布对中国沪深股市收益率分布特征作了实证研究；文献 [4] 提出了偏广义误差-Laplace (SGEL)分布并给出了SGEL分布的最大似然估计量和Fisher信息矩阵、构建了基于SGEL分布的风险度量模型、将POT模型中的超额分布用SGEL分布近似提出了POT-SGEL模型，这些可以用于金融市场中度量风险。Laplace分布模型的可靠性统计推断问题在国内外也得到了广泛的关注和研究。文献 [5] 研究了相互独立的顺序统计量 $X=\left(X_{\left(1\right)},X_{\left(2\right)},\cdots ,X_{\left(n\right)}\right)$ 服从参数为 $\lambda$ ( $\lambda >0$ )和 $\mu$ ( $\mu$ 为实常数)的拉普拉斯分布时的性质， $X_{\left(1\right)}$ 和 $X_{\left(n\right)}$ 的密度函数及它们的数字期望和方差；文献 [6] 讨论了标准Laplace分布极小和极大次序统计量的分布及在样本容量为2时，次序统计量分布的特点和它们之间的关系；文献 [7] 基于次序统计量样本研究了Laplace分布精确预测区间问题；文献 [8] 探讨了在测量误差的分布为Laplace分布时建立一种多元Laplace分布的测量误差模型，并将基于无条件期望的估计方法应用到其中；文献 [9] 基于卡方拟合优度检验和K-S检验方法构造了一类新的检验统计量对Laplace分布进行假设检验，最后通过统计模拟验证了该检验方法的有效性和可行性；文献 [10] 将Laplace分布的尺度参数的最短置信区间估计的求解问题转化为非线性方程组的求解问题；文献 [11] 在对数平方误差损失函数下研究了Laplace分布参数的最大最小估计问题。目前，Laplace分布也被应用到图形信号处理和模式识别等领域 [12] 。文献 [13] 根据多尺度几何分析方法Contourlet变换和平移不变Contourlet变换(TICT)高频系数重拖尾的特征，将数据分成两组，用广义Laplace分布对其无噪系数建模，高斯分布对其噪声系数建模，用分布迭代求得无噪系数在高频系数中的概率，最后用混合分布滤波方法降噪，在平滑噪声的同时较好的保持了图像的细节信息。文献 [14] 改进了基于拉普拉斯先验的贝叶斯压缩感知模型，消除了外部噪音的影响，提高了模型的抗噪性能和二维图像的重构性能。文献 [15] 通过建立混合泊松–拉普拉斯–高斯分布来表征电荷耦合器件(CCD)传感射线照相数据中的噪声，并开发了一个多凸优化模型来解决重建问题，对在动力实验中处于重要地位的阿贝尔反演层析成像做了进一步研究。

本文将在平方误差损失、LINEX损失和熵损失这三类损失函数下研究Laplace分布参数的Bayes估计问题，然后基于平方误差损失函数对以上三种风险函数进行比较，通过蒙特卡洛模拟考察各类估计的优良性，最后提出在实际应用Bayes估计时，如何针对n的取值来选择合适的Bayes估计。

设随机变量X服从两参数Laplace分布，相应的概率密度函数为

$f\left(x|\mu ,\theta \right)=\frac{1}{2\theta }\exp \left(-\frac{\left|x-\mu \right|}{\theta }\right),-\infty <x<\infty$ (1)

其中 $\mu \in \left(+\infty ,-\infty \right)$ 为位置参数， $\theta >0$ 为尺度参数。

2. Bayes估计

设 $X=\left(X_1,X_2,\cdots ,X_n\right)$ 来自总体服从Laplace分布(1)的容量为n的一个简单随机样本，其中位置参数 $\mu$ 已知。记 $x=\left(x_1,x_2,\cdots ,x_n\right)$ 为 $X=\left(X_1,X_2,\cdots ,X_n\right)$ 的样本值， $t={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|x_i-\mu \right|}$ 为 $T={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|X_i-\mu \right|}$ 的样本值。

给定样本值 $x=\left(x_1,x_2,\cdots ,x_n\right)$ 后，参数 $\theta >0$ 的似然函数为

$l\left(x;\theta \right)={\displaystyle \underset{i=1}{\overset{n}{\prod }}f\left(x_i|\mu ,\theta \right)}={\displaystyle \underset{i=1}{\overset{n}{\prod }}\frac{1}{2\theta }\exp \left(-\frac{\left|x_i-\mu \right|}{\theta }\right)}\propto {\theta }^{-n}{\text{e}}^{-\frac{t}{\theta }}$ (2)

通过求解对数似然方程得 $\theta$ 的最大似然估计：

${\hat{\delta }}_{MLE}=\frac{T}{n}$ (3)

易证 $T={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|X_i-\mu \right|}$ 服从参数为n和 ${\theta }^{-1}$ 伽玛分布 $\Gamma \left(n,{\theta }^{-1}\right)$ ，则有 $E{T}^{-1}=\theta /\left(n-1\right)$ 。

以下讨论中设参数 $\theta$ 的先验分布为无信息Quasi先验分布，即概率密度：

$\pi \left(\theta \right)\propto {\theta }^{-d},\theta >0,d>0$ (4)

本节讨论中所采用的损失函数为

1) 平方误差损失函数

$L\left(\hat{\theta },\theta \right)={\left(\hat{\theta }-\theta \right)}^2$ (5)

在该损失下参数 $\theta$ 的Bayes估计为：

${\hat{\theta }}_{BS}=E\left[\theta |X\right]$ . (6)

2) LINEX损失函数：

$L\left(\Delta \right)={\text{e}}^{c\Delta }-c\Delta -1,c\ne 0$ (7)

其中 $\Delta =\frac{\hat{\theta }-\theta }{\theta }$ ，c为形状参数。在该损失函数下， $\theta$ 的Bayes估计 ${\hat{\theta }}_{BL}$ 为方程(8)的解：

$E\left[\frac{1}{\theta }\exp \left(\frac{c{\hat{\theta }}_{BL}}{\theta }\right)|X\right]={\text{e}}^{c}E\left[\frac{1}{\theta }|X\right]$ (8)

3) 熵损失函数：

$L\left(\hat{\theta },\theta \right)=\frac{\hat{\theta }}{\theta }-\ln \frac{\hat{\theta }}{\theta }-1$ (9)

在该损失下，参数 $\theta$ 的Bayes估计为

${\hat{\theta }}_{BE}={\left[E\left({\theta }^{-1}|X\right)\right]}^{-1}$ (10)

以上三种损失函数的详细介绍以及它们在Bayes统计推断中的更多应用参见文献 [16] [17] [18] [19] [20] 。

定理 3.1 设 $X_1,X_2,\cdots ,X_n$ 为来自Laplace分布(1)的一个样本容量为n的简单随机样本，其中 $x_1,x_2,\cdots ,x_n$ 为相应的样本值，记 $x=\left(x_1,x_2,\cdots ,x_n\right)$ ， $X=\left(X_1,X_2,\cdots ,X_n\right)$ ， $t={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|x_i-\mu \right|}$ 为 $T={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|X_i-\mu \right|}$ 的样本值。并设参数 $\theta$ 的先验分布为Quasi先验分布(4)，则

1) 参数 $\theta$ 在平方误差损失下的Bayes估计为：

${\hat{\theta }}_{BS}=\frac{T}{n+d-2}$ , (11)

2) 参数 $\theta$ 在LINEX损失下的Bayes估计为：

${\hat{\theta }}_{BL}=\frac{T}{c}\left[1-\exp \left(-\frac{c}{n+d}\right)\right]$ (12)

3) 参数 $\theta$ 在熵损失下的Bayes估计为：

${\hat{\theta }}_{BE}=\frac{T}{n+d-1}$ (13)

证明 给定样本值 $x=\left(x_1,x_2,\cdots ,x_n\right)$ 后参数 $\theta$ 的似然函数为：

$l\left(\theta ;x\right)={\displaystyle \underset{i=1}{\overset{n}{\prod }}f\left(x_i|\mu ,\theta \right)}={\displaystyle \underset{i=1}{\overset{n}{\prod }}\frac{1}{2\theta }\exp \left(-\frac{\left|x_i-\mu \right|}{\theta }\right)}\propto {\theta }^{-n}{\text{e}}^{-\frac{t}{\theta }}$ ,

其中 $t={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|x_i-\mu \right|}$ 为 $T={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|X_i-\mu \right|}$ 的样本值。再由公式(4)和Bayes定理，我们可以得到参数 $\theta$ 的后验概率

密度函数为：

$h\left(\theta |x\right)\propto l\left(\theta |x\right)\cdot \pi \left(\theta \right)\propto {\theta }^{-n}{\text{e}}^{-t/\theta }{\theta }^{-d}\propto {\theta }^{-\left(n+d\right)}{\text{e}}^{-t/\theta }$ (14)

于是 $\theta$ 的后验分布为倒伽玛分布 $I\Gamma \left(n+d-1,s\right)$ ，即概率密度为：

$h\left(\theta |x\right)=\frac{t^{n+d-1}}{\Gamma \left(n+d-1\right)}{\theta }^{-\left(n+d\right)}{\text{e}}^{-\frac{t}{\theta }}$ (15)

则：

1) 参数 $\theta$ 在平方误差损失函数下的Bayes估计为：

${\hat{\theta }}_{BS}=E\left(\theta |X\right)=\frac{T}{n+d-2}$ ,

2) 由于

$\begin{array}{c}E\left[\frac{1}{\theta }\exp \left(\frac{c{\hat{\theta }}_{BL}}{\theta }\right)|X\right]={\displaystyle {\int }_0^{\infty }\frac{1}{\theta }\exp \left(\frac{c{\hat{\theta }}_{BL}}{\theta }\right)}\frac{T^{n+d-1}}{\Gamma \left(n+d-1\right)}{\theta }^{-\left(n+d\right)}{\text{e}}^{-\frac{T}{\theta }}\text{d}\theta \\ =\frac{T^{n+d-1}}{\Gamma \left(n+d-1\right)}\frac{\Gamma \left(n+d\right)}{{\left(T-c{\hat{\theta }}_{BL}\right)}^{n+d}}\end{array}$

和

$\begin{array}{c}{\text{e}}^{c}E\left[\frac{1}{\theta }|X\right]={\displaystyle {\int }_0^{\infty }\frac{1}{\theta }}\frac{T^{n+d-1}}{\Gamma \left(n+d-1\right)}{\theta }^{-\left(n+d\right)}{\text{e}}^{-\frac{T}{\theta }}\text{d}\theta \\ ={\text{e}}^c\cdot \frac{n+d-1}{T}\end{array}$

将它们代入式(8)，解得参数 $\theta$ 在LINEX损失下的Bayes估计为：

${\hat{\theta }}_{BL}=\frac{T}{c}\left[1-\exp \left(-\frac{c}{n+d}\right)\right]$

3) 参数 $\theta$ 在熵损失函数下的Bayes估计为：

$\begin{array}{c}{\hat{\theta }}_{BE}={\left[E\left({\theta }^{-1}|X\right)\right]}^{-1}\\ ={\left[{\displaystyle {\int }_0^{\infty }\frac{1}{\theta }}\frac{T^{n+d-1}}{\Gamma \left(n+d-1\right)}{\theta }^{-\left(n+d\right)}{\text{e}}^{-\frac{T}{\theta }}\text{d}\theta \right]}^{-1}\\ =\frac{T}{n+d-1}\end{array}$

3. 平方误差损失下各类估计的风险函数比较研究

为比较各类Bayes估计的好坏，风险函数是一个常用且重要的衡量标准。设 $\hat{\theta }$ 为 $\theta$ 的估计量， $L\left(\hat{\theta },\theta \right)$ 表示损失函数，则其对应的风险函数定义为：

$R\left(\theta ,\hat{\theta }\right)=E\left[L\left(\hat{\theta },\theta \right)\right]$ .

本节将推导各Bayes估计量在平方误差损失下的风险函数，并给出蒙特卡洛模拟比较结果。设 $\hat{\theta }$ 为 $\theta$ 的估计量，则在平方误差损失下， $\hat{\theta }$ 的风险函数为

$R\left(\theta ,\hat{\theta }\right)=E\left[{\left(\hat{\theta }-\theta \right)}^2\right]={\displaystyle {\int }_0^{\infty }{\left(\hat{\theta }-\theta \right)}^{2}h\left(s\right)\text{d}s}$ (16)

经简单的计算得，三类Bayes估计的风险函数分别为：

$R\left(\theta ,{\hat{\theta }}_{BS}\right)={\theta }^2\left[\frac{n\left(n+1\right)}{{\left(n+d-2\right)}^2}-\frac{2n}{n+d-2}+1\right]$ (17)

$R\left(\theta ,{\hat{\theta }}_{BL}\right)={\theta }^2\left[\frac{n\left(n+1\right)}{c^2}{\left(1-{\text{e}}^{-c/\left(n+d\right)}\right)}^2-\frac{2n}{c}\left(1-{\text{e}}^{-c/\left(n+d\right)}\right)+1\right]$ (18)

和

$R\left(\theta ,{\hat{\theta }}_{BE}\right)={\theta }^2\left[\frac{n\left(n+1\right)}{{\left(n+d-1\right)}^2}-\frac{2n}{n+d-1}+1\right]$ . (19)

为比较各风险函数，将各风险函数与 ${\theta }^2$ 做比值，得到如下三个比率风险函数：

$\frac{R\left(\theta ,{\hat{\theta }}_{BS}\right)}{{\theta }^2}=B_1$ ， $\frac{R\left(\theta ,{\hat{\theta }}_{BL}\right)}{{\theta }^2}=B_2$ 和 $\frac{R\left(\theta ,{\hat{\theta }}_{BE}\right)}{{\theta }^2}=B_3$

下面给出各风险函数与 ${\theta }^2$ 的比值函数 $B_1,B_2$ 和 $B_3$ 随n变化的曲线图。

由图1~4知，当n较小时，各风险函数与 ${\theta }^2$ 的比值函数 $B_1,B_2$ 和 $B_3$ 的图像差别较大，但随n的增大，特别是n较大，例如当n > 60时，各类曲线趋于重合，即三个比率风险函数值趋于一致。

Figure 1. The curves of ratio of risk function with d = 1.5, c = 1.5

图1. d = 1.5，c = 1.5时，各比率风险函数曲线

Figure 2. The curves of ratio of risk function with d = 1.5, c = 0.5

图2. d = 1.5，c = 0.5时，各比率风险函数曲线

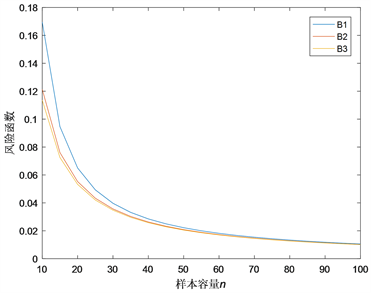
Figure 3. The curves of ratio of risk function with d = 0.5, c = −2.5

图3. d = 0.5，c = −2.5时，各比率风险函数曲线

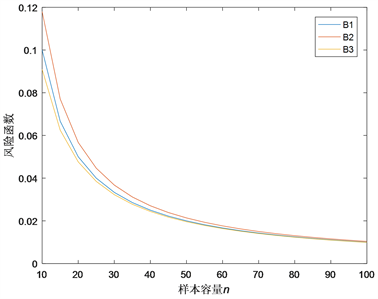
Figure 4. The curves of ratio of risk function with d = 2, c = 2.5

图4. d = 2，c = 2.5时，各比率风险函数曲线

4. 结论

针对Laplace分布模型参数的Bayes统计推断问题，本文在参数的先验分布为无信息Quasi先验时研究了其在三种常见损失函数下的Bayes估计问题。进一步地，在平方误差损失函数下通过统计模拟试验对各类Bayes估计的风险函数进行了比较。又由公式(18)，我们发现LINEX损失函数中的形状参数c不但影响估计值也会影响到参数的估计的风险函数值。根据模拟结果(参见图1~4)，我们建议在实际应用Bayes估计时，可采用如下原则：

1) 当n较小时，可以将图像中对应于超参数d的风险函数较小的Bayes估计作为参数的估计值。

2) 当n较大时，由于各Bayes估计受超参数d的影响较小，此时可任选一类Bayes估计作为参数的估计值。

基金项目

江西省教育厅科技项目，编号：GJJ211604。