基于有源功率解耦的小电容PFC变换器

Small Capacitance PFC Converter Based on Active Power Decoupling

摘要: 针对传统大容量电解电容PFC电路可靠性低、寿命短的缺点，论文研究了一种基于功率解耦的高可靠PFC变换器。它采用具备小容量薄膜电容的有源功率解耦电路替代传统PFC变换器的大容量的电解电容，通过控制有源功率解耦电路实现电容电压互补，从而有效避免电网二倍频脉动功率导致的母线电压脉动，同时提高PFC变换器的可靠性和使用寿命。论文详细分析了有源功率解耦电路工作原理，推导其数学模型，提供了电路参数的设计思路。最后，通过MATLAB软件仿真比较和验证该电路的可靠性。

Abstract: Aiming at the disadvantages of low reliability and short life of traditional large capacity electrolytic capacitor PFC circuit, a high reliability PFC converter based on power decoupling is studied in this paper. It uses an active power decoupling circuit with a small-capacity thin-film capacitor to replace the large-capacity electrolytic capacitor of the traditional PFC converter. By controlling the active power decoupling circuit, the capacitor and voltage complement each other, so as to effectively avoid the voltage pulsation of the bus caused by the power grid double frequency pulsation, and improve the reliability and service life of the PFC converter. This paper analyzes the working principle of active power decoupling circuit in detail, deduces its mathematical model, and provides the circuit parameter design idea. Finally, the reliability of the circuit is compared and verified by MATLAB simulation.

1. 引言

PFC变换器能够有效提高电网电流质量，因此在各类充电装置、家用空调及照明系统中都有着极其广泛的应用 [1] [2] [3] [4] 。在单相电网供电体系下，PFC输入瞬时功率为频率100 Hz的脉动量 [5] [6] 。为有效吸收电网脉动功率，实现直流母线电压稳定，目前常用的方法是在直流母线中并联一个大容量的电解电容器 [7] 。然而，电解电容存在寿命短的问题，极大降低了系统的可靠性 [8] 。

薄膜电容具有耐压高、ESR低、无极性、性能稳定、寿命长等优点 [9] ，用其替代电解电容可以有效解决传统系统寿命短的问题。但是，目前薄膜电容仍存在成本高/功率密度低的缺点，因此不能采用同值电容简单替换的技术方案。基于小容量薄膜电容的有源功率解耦电路可以精确控制电网脉动功率的吸收或释放，是提高PFC变换器可靠性的有效手段之一。文献 [10] 提出一种并联Buck/Boost双向变换器的无电解电容功率解耦电路，其变换器输出电能质量较高，但需通过电流互感器或电流传感器来检测解耦电路的电感电流，增加了电路的体积和成本。文献 [11] 提出了一种串联型功率解耦无电解电容PFC变换器拓扑，该方案的功率损耗较低，但辅助电路涉及了大量的开关器件与电容电感，这使得电路的成本与体积很难得到控制。文献 [12] 中通过控制薄膜电容上电压的正弦变化来补偿纹波，但这种波形可能包含高次谐波，这对于欠阻尼的二阶系统难以跟踪和控制。文献 [13] 采用完全相同的电路配置，提出在电容参考电压中注入直流偏置，使谐波含量变小。然而，由于电容器电压没有下降到零，所以它不会完全放电，这意味着薄膜电容器没有得到充分利用。上述文献所提出的各类解耦电路都能实现对电路中的电容减容，但存在成本较高、不易控制、不能充分利用器件等缺点。

论文研究了一种对称半桥有源功率解耦电路，并对其控制策略进行改进，通过在解耦电路的控制系统部分增加一个直流偏置因子来改变控制信号的占空比，从而提高薄膜电容器的利用率。仿真验证所改进后的PFC变换器的有效性。

2. 电网脉动功率特性分析

理想工况下，PFC变换器输出功率因数为1。基于此，交流侧电网电压与电流假设同频同相，则有交流侧电网电压瞬时值 $u_{ac}\left(t\right)$ 和电流瞬时值 $i_{ac}\left(t\right)$ ：

$u_{ac}\left(t\right)=\sqrt{2}{U}_{ac}\sin \left(\omega t\right)$ (1)

$i_{ac}\left(t\right)=\sqrt{2}{I}_{ac}\sin \left(\omega t\right)$ (2)

式中： $U_{ac}$ 为交流侧电网电压有效值； $I_{ac}$ 为交流侧电网电流有效值； $\omega$ 为电网自然角频率，且 $\omega =2\pi f$ ，其中f为电网频率。

根据式(1)和(2)可得电网瞬时功率 $p_{ac}\left(t\right)$ 为：

$p_{ac}\left(t\right)=2U_{ac}{I}_{ac}{\sin }^2\left(\omega t\right)=P_{dc}-P_{dc}\cos \left(2\omega t\right)$ (3)

$P_{dc}=U_{ac}{I}_{ac}$ (4)

由式(3)可以看出，电网瞬时功率由一个直流恒定功率和一个二倍频脉动功率组成，且二倍频分量的幅值与直流分量大小相等。由于PFC变换器直流侧输出功率恒定，因此电路中始终存在脉动功率，其表达式为：

$p_{2\omega }\left(t\right)=-P_{dc}\cos \left(2\omega t\right)$ (5)

为了消除脉动功率，PFC变换器一般会在电路中并联一个大电解电容。

电解电容在工作时充入的能量为：

$\Delta E=\frac{P_0}{\omega }=\frac{P_{dc}}{\omega }$ (6)

式中 $P_0$ 为交流侧平均功率，在不考虑变换器功率损耗，直流侧功率大小等于交流侧的功率平均值。另一方面电容储能的变化量由电容电压初始值和最终值决定，所以有：

$\Delta E=\frac{1}{2}C\left(U_{C\_\max }^2-U_{C\_\min }^2\right)$ (7)

比较(6)，(7)有

$\Delta U=\frac{P_0}{\omega U_{dc}C}$ (8)

根据(8)式可知，使用小容量薄膜电容会带来较大的纹波电压，导致PFC整体性能下降。

3. 基于功率解耦的高可靠小电容PFC变换器的设计

3.1. 电路拓扑

有源功率解耦电路基于小容量薄膜电容实现PFC变换器的功率解耦。图1是本文研究的对称半桥解耦电路，它由解耦电容C₁、C₂，滤波电感L_f，以及开关管Q₁和Q₂构成。其中电容C₁、C₂容值相等并串联构成PFC变换器的直流母线电容，两个电容中点通过滤波电感与开关管Q₁、Q₂连接。通过控制开关使波动能量在薄膜电容C₁和C₂之间传递，实现两个小容量薄膜电容电压互补，从而消除母线上的直流电压脉动。

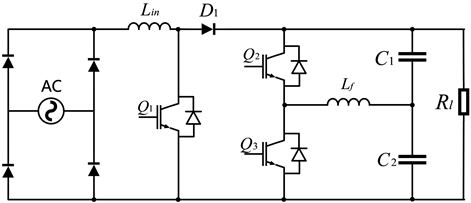
Figure 1. Main circuit topology of PFC converter

图1. PFC变换器主电路拓扑

3.2. 工作原理分析

解耦电路的工作模式根据C₁和C₂的能量传递方向不同，分为模式I和模式II。模式I中：C₁对C₂充电。假设开关Q₁导通，Q₂关断，电容C₁对电感L_f充电，电流方向如图2所示。当Q₁断开，Q₂导通，电感电流方向不变，L_f对C₂进行充电，如图2所示。模式II如图3所示，其工作原理与模式I类似。

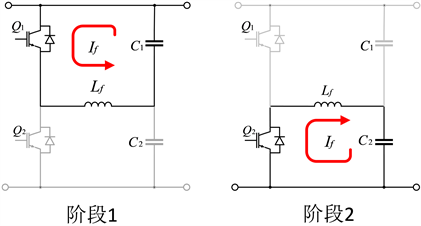
Figure 2. Inductor current flow in mode I

图2. 模式I下电感电流流向

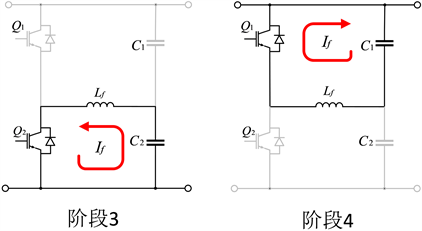
Figure 3. Inductor current flow in mode II

图3. 模式II下电感电流流向

可见通过控制Q₁、Q₂，能使电网脉动能量在薄膜电容C₁和C₂之间传递，避免电网脉动功率直接作用到直流母线，达到功率解耦的目的。图1所示电路中有 $C_1=C_2=C_f$ ，对应电压分别是 $u_{c1}\left(t\right)$ 和 $u_{c2}\left(t\right)$ ：

$\begin{array}{l}{u}_{c1}\left(t\right)=\frac{U_{dc}}{2}+V_c\sin \left(\omega t+\theta \right)\\ u_{c2}\left(t\right)=\frac{U_{dc}}{2}-V_c\sin \left(\omega t+\theta \right)\end{array}$ (9)

式中 $\theta$ 为电容电压 $u_{c1}\left(t\right)$ 与输入电压 $u_{in}\left(t\right)$ 之间的相位角， $\omega$ 为基本角频率。 $V_c$ 为薄膜电容器电压幅值。由(9)可得电容电流 $i_{c1}\left(t\right)$ 和 $i_{c2}\left(t\right)$ 为：

$\begin{array}{l}{i}_{c1}\left(1\right)=I_c\cos \left(\omega t+\theta \right)=\omega C_f{V}_c\cos \left(\omega t+\theta \right)\\ i_{c2}\left(1\right)=-I_c\cos \left(\omega t+\theta \right)=-\omega C_f{V}_c\cos \left(\omega t+\theta \right)\end{array}$ (10)

式中 $I_c$ 为滤波后电容电流的幅值。由(9)，(10)两式可得瞬时功率电容C₁/C₂瞬时功率之和 $p_c\left(t\right)$ 为：

$\begin{array}{c}{p}_c\left(t\right)=u_{c1}\left(t\right)i_{c1}\left(t\right)+u_{c2}\left(t\right)i_{c2}\left(t\right)\\ =\omega C_f{V}_c^2\sin \left(2\omega t+2\theta \right)\end{array}$ (11)

进一步，根据(10)式可得滤波器电感L_f的电流及其瞬时功率 $p_{Lf}\left(t\right)$ 分别为：

$\begin{array}{c}{i}_{Lf}\left(t\right)=i_{c1}\left(t\right)-i_{c2}\left(t\right)\\ =2I_c\cos \left(\omega t+\theta \right)=2\omega C_f{V}_c\cos \left(\omega t+\theta \right)\end{array}$ (12)

$\begin{array}{c}{p}_{Lf}\left(t\right)=L_f\frac{\text{d}{i}_{Lf}\left(t\right)}{\text{d}t}{i}_{Lf}\left(t\right)\\ =-2\omega L_f{\left(\omega C_f{V}_c\right)}^2\sin \left(2\omega t+2\theta \right)\end{array}$ (13)

根据(11) (13)可以求得对称半桥电路总瞬时功率 $p_{hb}\left(t\right)$ 为：

$\begin{array}{c}{p}_{hb}\left(t\right)=p_c\left(t\right)+p_{Lf}\left(t\right)\\ =\left[\omega C_f{V}_c^2-2\omega L_f{\left(\omega C_f{V}_c\right)}^2\right]\sin \left(2\omega t+2\theta \right)\end{array}$ (14)

通过上式可知滤波电感可能会降低改功率解耦电路的补偿能力，所以其值设计的要尽可能小。

PFC电路的瞬时功率 $p_{PFC}\left(t\right)$ 为输入电压 $u_{in}\left(t\right)$ 和电流 $i_{in}\left(t\right)$ 乘积加上电感 $L_{in}$ 上的瞬时功率，对应的公式如下：

$\begin{array}{l}{u}_{in}\left(t\right)=V_{in}\left|\sin \left(\omega t\right)\right|\\ i_{in}\left(t\right)=I_{in}\left|\sin \left(\omega t\right)\right|\end{array}$ (15)

$\begin{array}{c}{p}_{PFC}\left(t\right)=p_{in}\left(t\right)+p_{Lin}\left(t\right)\\ =u_{in}\left(t\right)i_{in}\left(t\right)+L_{in}\frac{\text{d}{i}_{in}\left(t\right)}{\text{d}t}{i}_{in}\left(t\right)\\ =\frac{V_{in}{I}_{in}}{2}-\frac{V_{in}{I}_{in}}{2}\cos \left(2\omega t\right)+\frac{\omega L_{in}{I}_{in}^2}{2}\sin \left(2\omega t\right)\end{array}$ (16)

将(14)和(16)的时变项相等，可以推导出

$\theta =\frac{1}{2}\arctan \left(-\frac{V_{in}{I}_{in}}{\omega L_{in}{I}_{in}^2}\right)=\frac{1}{2}\arctan \left(-\frac{V_{in}}{\omega L_{in}{I}_{in}}\right)$ (17)

$V_c=\sqrt{\frac{\sqrt{{\left(\frac{V_{in}{I}_{in}}{2}\right)}^2+{\left(\frac{\omega L_{in}{I}_{in}^2}{2}\right)}^2}}{\omega C_f-2\omega L_f{\left(\omega C_f\right)}^2}}$ (18)

上述公式表明：C₁和C₂的电压参考值和PFC变换器的功率以及电容值有关。如果能控制C₁和C₂电压如(17) (18)，则能实现电容有效吸收电网脉动功率，从而抑制直流母线电压纹波。

3.3. 关键参数计算

已知当 $V_c=\frac{U_{dc}}{2}$ 时，对称半桥电路可提供最大脉动功率：

$\omega C_f{V}_c^2=\frac{V_{in}{I}_{in}}{2}\text{and}\frac{\omega C_f{U}_{dc}^2}{4}=p_{in}$ (19)

$C_{eq}=\frac{C_f}{2}=\frac{2p_{in}}{\omega U_{dc}^2}$ (20)

其中 $p_{in}$ 为输入脉动功率幅值， $C_{eq}$ 为等效直流母线电容。该电路中电感 $L_g$ 和 $L_f$ 可由下式计算得到

$L_x=\frac{U_{dc}}{8f_s\Delta I_x}$ (21)

式中 $\Delta L_x$ 为电感 $L_f$ 或 $L_g$ 的电流纹波。

4. 控制原理

图4显示了PFC电路控制系统的总体框架。主电路采用双环控制，输出的直流母线电压经采样与输出电压的给定值比较，偏差量经过电压环PI调节器后与归一化后的直流侧输入电压相乘作为电流环的给定值，再引入输入电流与给定值比较，偏差经过电流环PI调节器，作为信号波，通过PWM波的方式控制开关管的占空比最终实现对电流的控制。

Figure 4. Composition of control system

图4. 控制系统组成

功率解耦控制电路采用双环控制方案实现功率解耦，外部控制器用于调节直流母线电压纹波为零，并为滤波器电感电流 $i_{Lf}$ 产生电流参考 $i_{Lf}^{*}$ ，电流环采用比例控制器控制。在图4中，直流电压的误差反馈到电源去耦环，PR调谐时采用的频率为 $2\omega$ 和 $4\omega$ ，以抑制直流中的纹波电压。内环控制器输出的直流偏置因子k被设置为0.8，这样即使在电容变化的极端情况下，半桥也能保持直流电压的完好。

其中PR控制器的公式为：

$G_{PR\_P}\left(s\right)=k_{pp}+{\displaystyle \underset{h=2,4}{\sum }\frac{k_{ip}s}{s^2+{\left(h\omega \right)}^2}}$ (22)

其中 $k_{pp}$ 和 $k_{ip}$ 分别为控制器增益。

5. 仿真结果及分析

基于MATLAB/simulink仿真软件对本文所研究的基于功率解耦的高可靠小电容PFC变换器进行验证。将传统的PFC变换器与本文所改进后的基于功率解耦的高可靠小电容变换器进行对比分析。传统的PFC电路与本文所研究的PFC电路输出功率与电压要求一致。表1为有源功率解耦电路关键参数。

Table 1. Key parameters of active power decoupling circuit

表1. 有源功率解耦电路关键参数

图5是直流侧电压仿真波形对比，通过图可以看出，相同主电路和控制电路下，高可靠性PFC输出电压在400V上下波动10V左右，而传统PFC变换器并联一个200 μF的电解电容，其输出电压波动达到了40V，本文研究的PFC变换器能很好地抑制输出电压的波动。

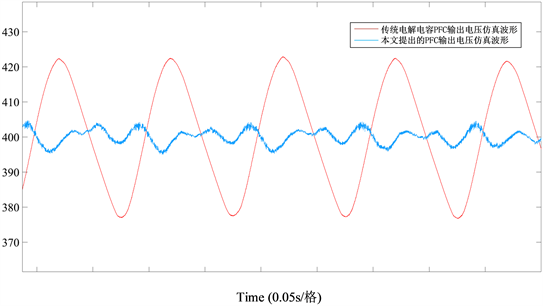
Figure 5. Output DC voltage simulation waveform

图5. 输出直流电压仿真波形

(a)(b)

Figure 6. Simulation waveform of power grid current. (a) Grid current and voltage simulation waveform of PFC converter studied in this paper; (b) Grid current and voltage simulation waveform of traditional PFC converter

图6. 电网电流的仿真波形。(a) 本文研究的PFC变换器电网电流和电压仿真波形；(b) 传统PFC变换器电网电流和电压仿真波形

图6(a)显示本文研究的PFC变换器电网电流与电流相位几乎相同，电网电流接近正弦，在谐波次数最大值40倍、测量2个周期的情况下THD达到5%。而在相同测量条件下，传统PFC电网电流THD达到了30%。本文研究的PFC电路降低了电网电流的谐波失真。

图7是两个薄膜电容C₁和C₂两端电压仿真波形，可以看出电压波形满足公式(9)，验证了本文研究的控制策略的正确性。

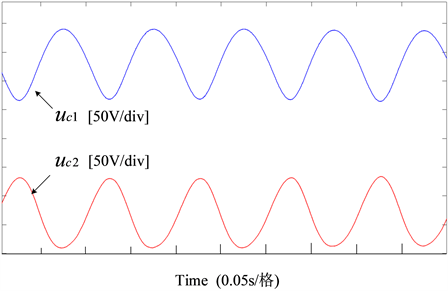
Figure 7. Capacitor and voltage on both sides of capacitor

图7. 电容C₁和电容C₂两侧电压

6. 总结

本文研究了一种新型解耦电路及对应的控制，与传统电路的大电解电容相比，该电路采用了高可靠性的小薄膜电容作为功率解耦器件，极大地提高了PFC变换器的使用寿命和可靠性。本文对解耦电路的控制原理和设计过程进行了详细分析，得出以下结论：

1) 基于功率解耦的小薄膜电容系统能有效地解决交流侧所带来的脉动功率的影响，且该系统所需辅助电路的器件较少，更易控制。

2) 通过对紧凑型小电容系统进行仿真验证，结果表明该系统能有效地实现直流侧并联电容的容值降容，交流侧电网电流的THD也有显著降低，证明了该方案的可行性。

3) 对比其它基于功率解耦的小电容系统，所提出的变换器的体积和成本也较小，更为符合我国可持续发展的战略目标。